2.5.3: Funciones Trig y Radianes con Tecnología
- Page ID
- 107694
Grados versus radianes y modos de calculadora.
Seis funciones trigonométricas y radianes
Mientras trabajas algún día en tu clase de matemáticas, se te da una hoja de valores en radianes y se te pide que encuentres las diversas funciones trigonométricas de los mismos, como seno, coseno y\ tan gent. La primera pregunta te pide que encuentres el\(\sin \dfrac{\pi }{6}\). Estás a punto de comenzar a convertir las mediciones en radianes en grados cuando te preguntas si podría ser posible simplemente tomar los valores de las funciones directamente.
¿Crees que esto es posible? Resulta que de hecho es posible aplicar funciones trigonométricas a las mediciones en radianes. Aquí aprenderás a hacer precisamente eso.
Funciones trigonométricas y radianes
A pesar de que estás acostumbrado a realizar las funciones trigonométricas en grados, seguirán funcionando en radianes. La única diferencia es la forma en que se ve el problema. Si ves\(\sin \dfrac{\pi }{6}\), eso está quieto\(\sin 30^{\circ} \) y la respuesta es quieta\(\dfrac{1}{2}\).
La mayoría de las calculadoras científicas y gráficas tienen una configuración MODE que le permitirá convertir entre las dos, o encontrar aproximaciones para funciones trigonométricas usando cualquiera de las medidas. Es impor\ tan t que si estás usando tu calculadora para estimar una función trigonométrica sepas qué modo estás usando. Mira la siguiente pantalla:
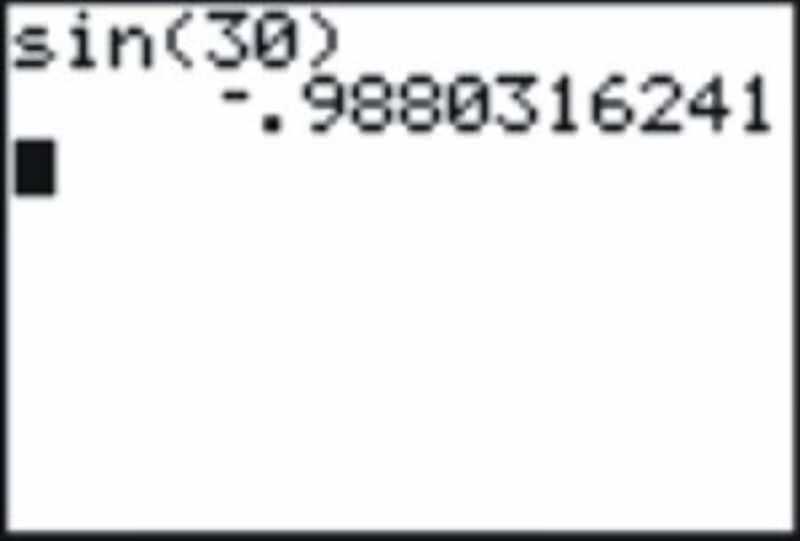
Si entraste a esto esperando encontrar el seno de 30 grados te darías cuenta de que algo anda mal porque la respuesta debería ser\(\dfrac{1}{2}\). De hecho, como habrás sospechado, la calculadora está interpretando esto como 30 radianes. En este caso, cambiar el modo a grados y recalcular dará el resultado esperado.

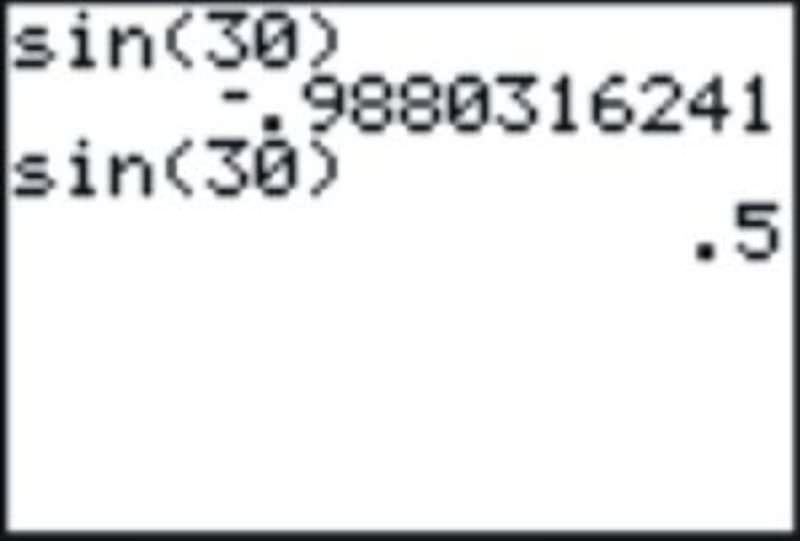
Las calculadoras científicas suelen tener una pantalla de 3 letras que muestra grados o RAD para indicarle en qué modo se encuentra la calculadora.
Echemos un vistazo a algunos problemas de ejemplo.
1. Encuentra\(\tan \dfrac{3\pi }{4}\).
Si es necesario,\(\dfrac{3\pi }{4}\) conviértase a grados. Haciendo esto, encontramos que es 1\(35^{\circ} \). Entonces, esto es\(\tan 135^{\circ} \), que es -1.
2. Encuentra el valor de\(\cos \dfrac{11 \pi }{6}\).
Si es necesario,\(\dfrac{11 \pi }{6}\) conviértase a grados. Haciendo esto, encontramos que lo es\(330^{\circ} \). Entonces, esto es\(\cos 330^{\circ} \), que es\(\dfrac{\sqrt{3}}{2}\).
3. Convertir 1 radián a medida de grado.
Muchos estudiantes se acostumbran tanto a usar\(\pi \) en la medida de radianes que incorrectamente piensan que 1 radián significa\(1\pi \) radianes. Si bien es más conveniente y común expresar medida radianes en términos de\(\pi \), no pierdas de vista que\(\pi \) los radianes son un número. Especifica un ángulo creado por una rotación de aproximadamente 3.14 longitudes de radio. Entonces, 1 radián es una rotación creada por un arco que es solo de un solo radio de longitud.
\(\text{radians } \times \dfrac{180}{\pi }=\text{degrees}\)
Entonces 1 radián serían\(\dfrac{180}{\pi }\) grados. El uso de cualquier calculadora científica o gráfica dará una aproximación razonable para esta medida de grado, aproximadamente\(57.3^{\circ} \).
Antes, se le pidió que encontrara\(\sin \dfrac{\pi }{6}\).
Solución
Como has aprendido en esta sección, el\(\sin \dfrac{\pi }{6}\) es lo mismo que\(\sin 30^{\circ} \), que es igual\(\dfrac{1}{2}\). Puedes encontrar esto ya sea convirtiendo\(\dfrac{\pi }{6}\) a grados, o usando tu calculadora con ángulos ingresados en radianes.
Usando una calculadora, encuentre la medida aproximada del grado (al décimo más cercano) del ángulo expresado en radianes:
Solución
\(\dfrac{6\pi }{7}\)
\(154.3^{\circ}\)
Usando una calculadora, encuentre la medida aproximada del grado (al décimo más cercano) del ángulo expresado en radianes:
Solución
\(\dfrac{20\pi }{11}\)
\(327.3^{\circ}\)
Gina quiso calcular el\(\sin 210^{\circ} \) y obtuvo la siguiente respuesta en su calculadora:
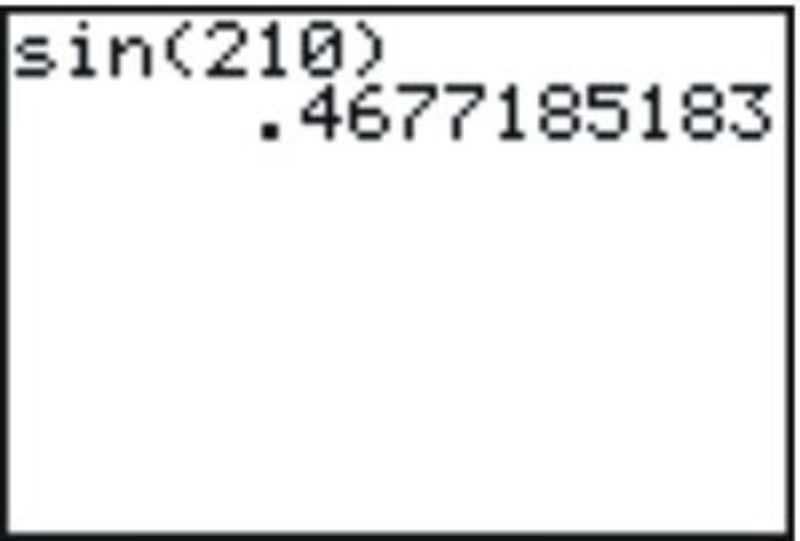
Solución
Afortunadamente, Kylie vio su respuesta y le dijo que obviamente era incorrecta.
- Escribe la respuesta correcta, en forma radical más simple.
- Explique lo que hizo mal.
La respuesta correcta es\(−\dfrac{1}{2}\). Su calculadora era es el modo equivocado y ella calculó el seno de 210 radianes.
Revisar
Usando una calculadora, encuentra la medida aproximada del grado (al décimo más cercano) del ángulo expresado en radianes.
- \(\dfrac{4 \pi }{7}\)
- \(\dfrac{5 \pi }{6}\)
- \(\dfrac{8 \pi }{11}\)
- \(\dfrac{5 \pi }{3}\)
- \(\dfrac{8 \pi }{3}\)
- \(\dfrac{7 \pi }{4}\)
- \(\dfrac{12 \pi }{5}\)
Encuentra el valor de cada uno usando tu calculadora.
- \(\sin \dfrac{3\pi }{2}\)
- \(\cos \dfrac{\pi }{2}\)
- \(\tan \dfrac{\pi }{6}\)
- \(\sin \dfrac{5 \pi }{6}\)
- \(\tan \dfrac{4 \pi }{3}\)
- \(\cot \dfrac{7 \pi }{3}\)
- \(\sec \dfrac{11 \pi }{6}\)
- ¿Crees que los radianes siempre estarán escritos en términos de\ pi? ¿Es posible tener, por ejemplo, exactamente 2 radianes?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.3.
El vocabulario
| Término | Definición |
|---|---|
| radián | Un radián es una unidad de ángulo que es igual al ángulo creado en el centro de un círculo cuyo arco es igual en longitud al radio. |

