2.5.4: Rotaciones en Radianes
- Page ID
- 107682
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Rotación de manecillas de reloj.
En tu clase de matemáticas una mañana terminas un cuestionario temprano. Mientras esperas, miras el reloj mientras se apaga cinco minutos. La hora en el reloj dice 9:00. Tus lecciones recientes te han enseñado que una forma de medir la posición de algo en un círculo es usar un ángulo. De pronto se te ocurre que esto se puede aplicar a los relojes. ¿Se puede determinar el ángulo entre las dos manecillas del reloj?
Mucha información interesante sobre las rotaciones y cómo medirlas puede provenir de mirar relojes. Estamos tan familiarizados con los relojes en nuestra vida diaria que no solemos detenernos a pensar en estos pequeños dispositivos, con las manos rotando continuamente. Tomemos unos minutos en esta lección para echar un vistazo más de cerca a estos ejemplos de movimiento rotacional.
Para los siguientes problemas, expresemos en radianes
1. Las manecillas de un reloj muestran 11:20. Exprese el ángulo obtuso formado por las manecillas de las horas y los minutos en medida radianes.
El siguiente diagrama muestra la ubicación de las manecillas a la hora especificada.
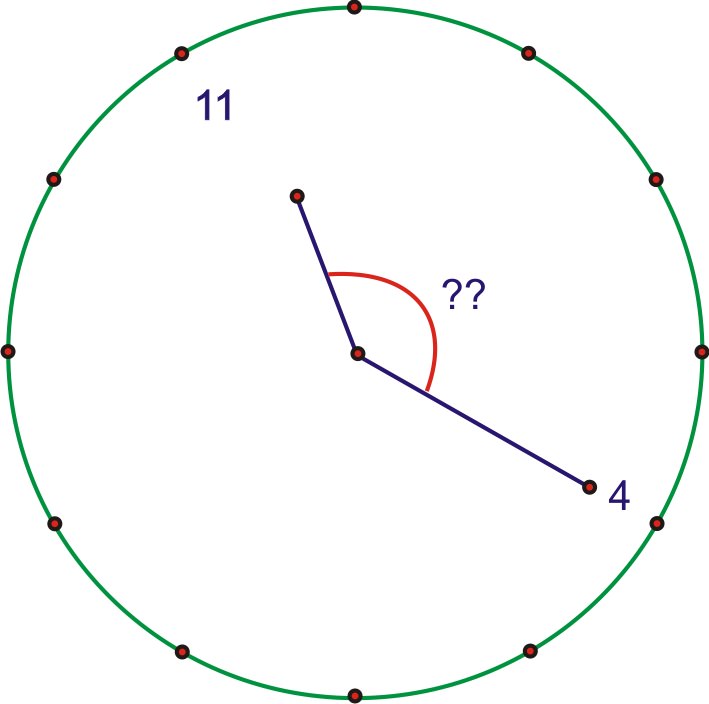
Debido a que hay 12 incrementos en un reloj, el ángulo entre cada marca de hora en el reloj es\(\dfrac{2\pi }{12}=\dfrac{\pi }{6}\) (o\(30^{\circ} \)). Entonces, el ángulo entre el 12 y el 4 es\(4\times \dfrac{\pi }{6}=\dfrac{2\pi }{3}\) (o\(120^{\circ}\)). Debido a que la rotación de 12 a 4 es un tercio de una rotación completa, parece razonable suponer que la manecilla de las horas se mueve continuamente y por lo tanto se ha movido un tercio de la distancia entre el 11 y el 12. Esto quiere decir que el ángulo entre la manecilla de las horas y el 12 es de dos tercios de la distancia entre el 11 y el 12. Entonces,\(\dfrac{2}{3}\times \dfrac{\pi }{6}=\dfrac{2\pi }{18}=\dfrac{\pi }{9}\), y la medida total del ángulo es por lo tanto\(\dfrac{\pi }{9}+\dfrac{2\pi }{3}=\dfrac{\pi }{9}+\dfrac{6\pi }{9}=\dfrac{7\pi }{9}\).
2. Expreso en radianes
Las manecillas de un reloj muestran 4:15. Expresar el ángulo agudo formado por las manecillas de las horas y los minutos en medida radianes.
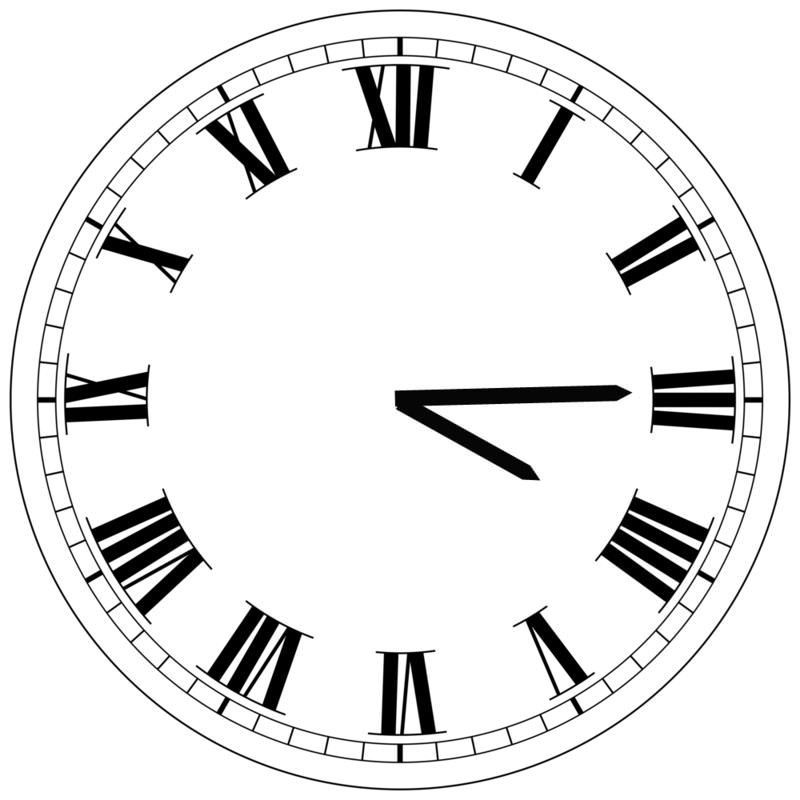
Debido a que hay 12 incrementos en un reloj, el ángulo entre cada marca de hora en el reloj es\(\dfrac{2\pi }{12}=\dfrac{\pi }{6}\) (o\(30^{\circ} \)). Entonces, el ángulo entre el 3 (que es donde se encuentra el minutero cuando es 15 minutos después de la hora) y el 4 es\(\dfrac{\pi }{6}\) (o\(30^{\circ}\)). Además, dado que la manecilla de minutos se ha movido una cuarta parte del recorrido alrededor de la hora, podemos inferir que la manecilla de las horas se ha movido una cuarta parte del camino entre cuatro y cinco, que es\(\dfrac{1}{4}\times \dfrac{\pi }{6}=\dfrac{\pi }{24}\). Sumando estos números da:\(\dfrac{\pi }{6}+\dfrac{\pi }{24}=\dfrac{4\pi }{24}+\dfrac{\pi }{24}=\dfrac{5\pi }{24}\).
3. Las manecillas de un reloj muestran las 2:30. Expresar el ángulo agudo formado por las manecillas de las horas y los minutos en medida radianes.
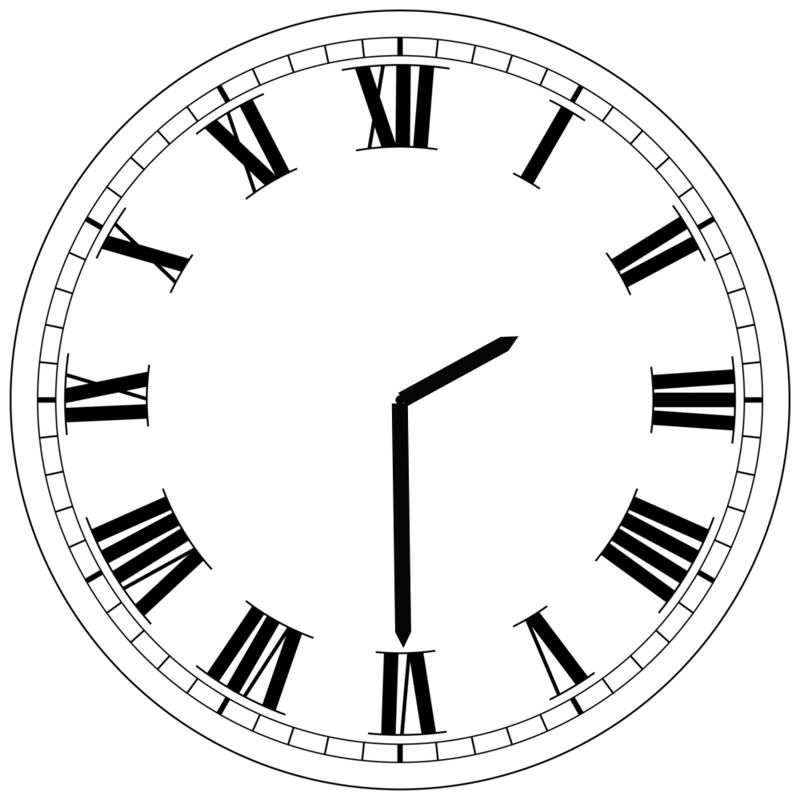
Debido a que hay 12 incrementos en un reloj, el ángulo entre cada marca de hora en el reloj es\(\dfrac{2\pi }{12}=\dfrac{\pi }{6}\) (o\(30^{\circ} \)). Dado que la manecilla de las horas estaría realmente a mitad de camino entre la 2 y la 3 a las 2:30, comience por determinar la distancia angular entre la 3 y la 6, luego puede agregar la porción adicional entre la 2 y la 3:
- El ángulo entre el 3 y el 6 (que es donde está el minutero a los 30 minutos después de la hora) es\(3\times \dfrac{\pi }{6}=\dfrac{3\pi }{6}=\dfrac{\pi }{2}\) (o\(90^{\circ} \)).
- Debido a que la rotación de 12 a 6 es la mitad de una rotación completa, parece razonable suponer que la manecilla de las horas se mueve continuamente y por lo tanto se ha movido la mitad de la distancia entre el 2 y el 3. Esto significa que el ángulo entre la manecilla de las horas y el 3 es la mitad de la distancia entre el 2 y el 3. Entonces,\(\dfrac{1}{2}\times \dfrac{\pi }{6}=\dfrac{\pi }{12}\).
- Por lo tanto, la medida total del ángulo es\(\dfrac{\pi }{12}+\dfrac{\pi }{2}=\dfrac{\pi }{12}+\dfrac{6\pi }{12}=\dfrac{7\pi }{12}\).
Anteriormente, te preguntaron si puedes determinar el ángulo entre las dos manecillas de un reloj.
Solución
Ya que ahora sabes que el ángulo entre las horas en un reloj es\(\dfrac{\pi }{6}=30^{\circ} \), puedes usar esta información para construir una respuesta. Hay tres horas entre las 9 y las 12 en un reloj, por lo que la respuesta es:
\(3\times \dfrac{\pi }{6}=\dfrac{3\pi }{6}=\dfrac{\pi }{2}=90^{\circ}\)
Entonces hay\(90^{\circ} \) grados entre el 9 y el 12 en el reloj.
En la siguiente imagen se muestra un reloj de 24 horas.

¿Cuál es el ángulo entre cada número del reloj expresado en medida exacta de radianes en términos de\(\pi \)?
Solución
Como hay\(2\pi \) radianes en un círculo, y hay 24 incrementos separados, la respuesta es\(\dfrac{2\pi }{24}=\dfrac{\pi }{12}\)
¿Cuál es el ángulo entre cada número del reloj expresado a la décima más cercana de un radián? ¿Qué pasa con la medida de grado?
Solución
Dado que hay\(2\pi \) radianes en un círculo, el número de radianes en cada una de las 24 divisiones diferentes es\(\dfrac{2\pi }{24}\approx .3\). En grados podemos hacer lo mismo tomando el número de grados en un círculo y dividiéndolo por 12:\(\dfrac{360}{24}=15^{\circ} \).
Estimar la medida del ángulo entre las manecillas en el momento mostrado al grado completo más cercano. Y luego en medida radianes en términos de\(\pi \).
Solución
\(20^{\circ} \). Las respuestas pueden variar, cualquier cosa por encima\(15^{\circ} \) y menos de\(25^{\circ} \) lo razonable. En radianes, esto es\(\dfrac{\pi }{9}\). Nuevamente, las respuestas pueden variar.
Revisar
Usa el reloj a continuación para ayudarte a encontrar el ángulo entre la manecilla de las horas y la manecilla de minutos en cada uno de los siguientes horarios. Exprese su respuesta en grados menores que\(180^{\circ} \). Entonces expresa tu respuesta en medida radianes en términos de\(\pi \).
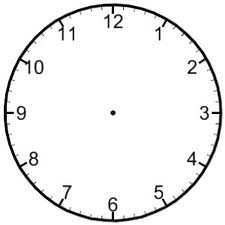
- 3:30
- 5:15
- 4:45
- 6:30
- 6:15
- 2:30
- 12:30
- 9:30
- 10:15
- 11:30
- 3:45
- 2:15
- 7:15
- ¿Cuántas veces en 12 horas se superpondrán las manecillas de las horas y los minutos?
- ¿Cuándo es la primera vez después de las 12:00 que las manecillas de horas y minutos se superponen exactamente?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.4.
El vocabulario
| Término | Definición |
|---|---|
| radián | Un radián es una unidad de ángulo que es igual al ángulo creado en el centro de un círculo cuyo arco es igual en longitud al radio. |
Recursos adicionales
Video: Ejemplos: Determinar ángulos de rotación
Práctica: Rotaciones en Radianes

