2.5.6: Longitud de un Arco
- Page ID
- 107676
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Radio multiplicado por el ángulo en radianes.
Has llevado a tu primo pequeño al parque de diversiones por el día. Mientras está ahí, decide que le gustaría un paseo en el carrusel. Después del paseo, ella rebota emocionada hacia ti. A ella le sorprende que haya dado vueltas, pero de alguna manera “no fue a ningún lado”, ya que terminó por donde empezó.
“¿Hasta dónde llegué cuando estaba a la mitad de la vuelta?” , ella pregunta.
Sabes que el radio del carrusel es de 7 metros. ¿Puedes decirle a tu primo pequeño qué tan lejos llegó en media vuelta alrededor del paseo?
La longitud de un arco en un círculo depende tanto del ángulo de rotación como de la longitud del radio del círculo. Si recuerda de la última lección, la medida de un ángulo en radianes se define como la longitud del arco cortada por una longitud de radio. ¿Y si el radio es de 4 cm? Entonces, la longitud del arco semicírculo se\(\pi \) multiplicaría por la longitud del radio, o\(4\pi \) cm de longitud.
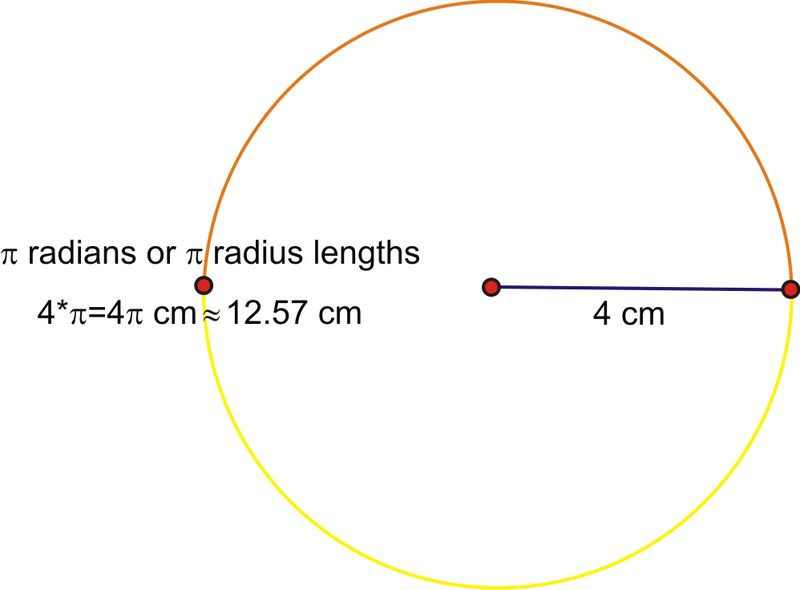
Esto da como resultado una fórmula que se puede utilizar para calcular la longitud de cualquier arco.
\(s=r\theta \),
donde s es la longitud del arco, r es el radio, y\ theta es la medida del ángulo en radianes.
Resolver esta ecuación para nos\(\theta \) dará una fórmula para encontrar la medida del radián dada la longitud del arco y la longitud del radio.
Veamos algunos problemas relacionados con la longitud del arco.
1. Encuentra la longitud de los arcos
La línea de tiros libres en una cancha de baloncesto de la NCAA tiene 12 pies de ancho. En competencia internacional, solo se trata de 11.81 pies. ¿Cuánto dura el semicírculo por encima de la línea de tiros libres en la cancha de la NCAA?
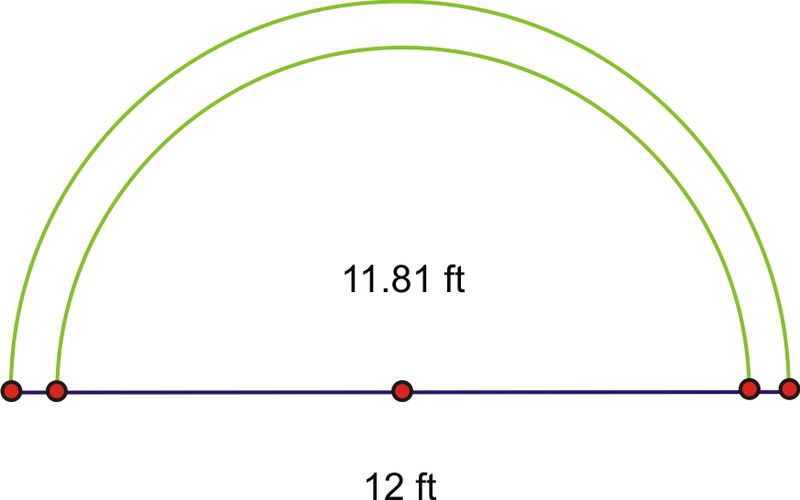
Encuentra ambas longitudes de arco.
\ (\ begin {array} {l}
\ text {NCAA} &\ text {INTERNATIONAL}\\
s_ {1} =r\ theta & s_ {2} =r\ theta\\
s_ {1} =\ dfrac {12} {2} (\ pi) & s_ {2}\ approx\ dfrac {11.81} {2} (\ pi)\
s_ _ {1} =6\ pi & s_ {2}\ aprox 5.905\ pi
\ end {array}\)
Entonces la respuesta es aproximadamente\(6\pi −5.905\pi \approx 0.095\pi\)
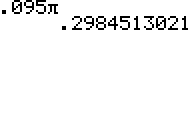
Esto es aproximadamente 0.3 pies, o aproximadamente 3.6 pulgadas más largo.
2. Dos engranajes conectados están girando. El engranaje más pequeño tiene un radio de 4 pulgadas y el radio del engranaje más grande es de 7 pulgadas. ¿Cuál es el ángulo a través del cual el engranaje más grande ha girado cuando el engranaje más pequeño ha hecho una rotación completa?
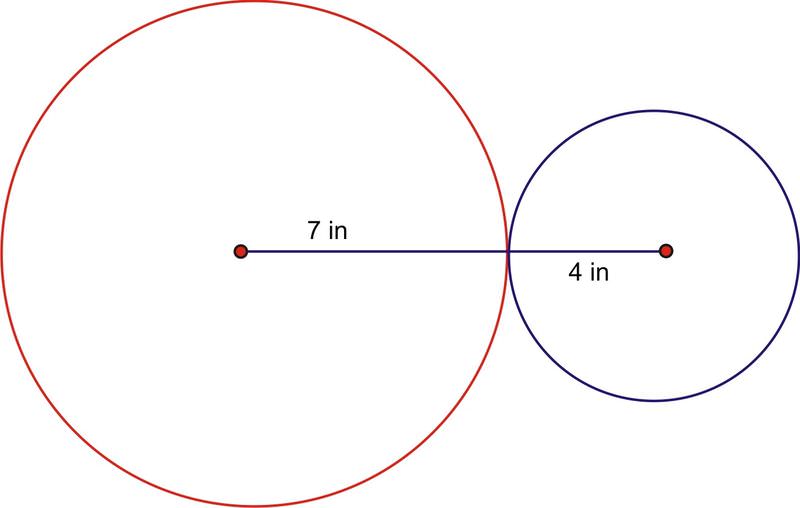
Debido a que el engranaje azul realiza una rotación completa, la longitud del arco recorrido es:
\(\begin{aligned} s &=r\theta \\ s&=4\times 2\pi \end{aligned}\)
Entonces, una longitud de\(8\pi \) arco en el círculo más grande formaría un ángulo de la siguiente manera:
\(\begin{aligned} \theta &=\dfrac{s}{r} \\ \theta &=\dfrac{8\pi }{7} \\ \theta &\approx 3.6 \end{aligned}\)
Por lo que el ángulo es de aproximadamente 3.6 radianes.
\(3.6\times 180\pi \approx 206^{\circ}\)
3. El radio de una llanta de automóvil estándar es de 27.94 cm. ¿Hasta dónde llega un auto en una revolución de la llanta?
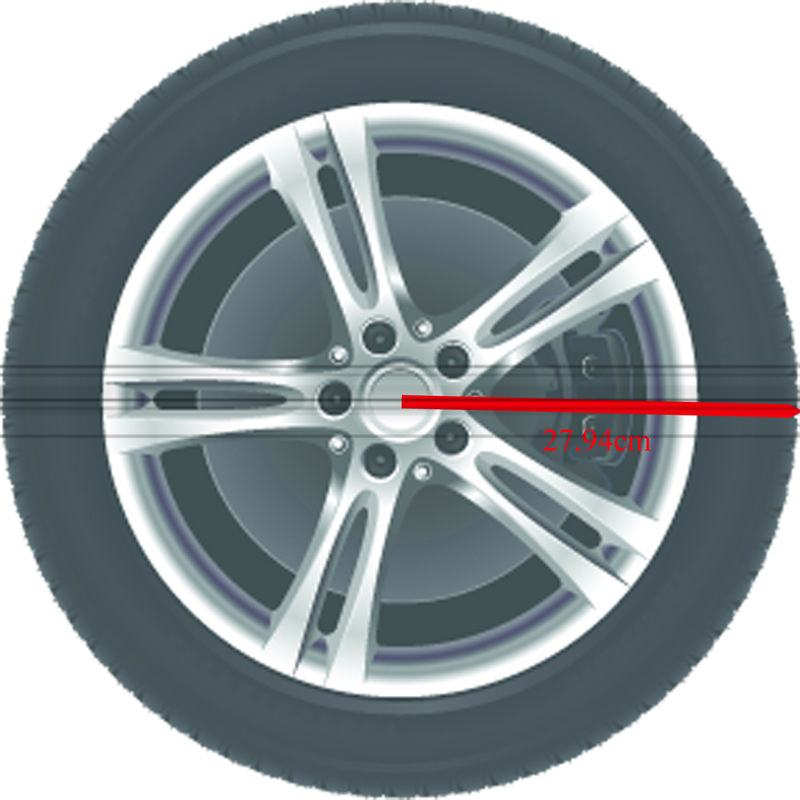
Dado que la distancia recorrida por la llanta es igual a la distancia alrededor de la llanta, podemos usar la circunferencia de la llanta para responder a la pregunta.
\(\begin{aligned} s &=r\theta \\ s&=(27.94)(2\pi )\\s=175.46 \end{aligned}\)
Antes, te preguntaron ¿puedes decirle a tu prima pequeña qué tan lejos llegó en media vuelta alrededor del paseo?
Solución
Ya que ahora sabes que puedes medir una longitud de arco usando\(s=r\theta \), puedes usar esto para encontrar una solución a la pregunta de tu primo. Ya que tu prima quiere saber hasta dónde se fue cuando se fue\(\dfrac{1}{2}\) de una rotación, y el radio del paseo es de 7 metros, puedes calcular su longitud de arco:
\(s=r\theta =7\pi \approx 21.98 \text{ meters}\)
Estás tratando de empujar tu auto después de que se haya averiado. Desafortunadamente, no eres muy fuerte, por lo que el auto simplemente se balancea de un lado a otro en lugar de rodar mientras empujas. Si el radio de la llanta de tu auto es de 14 pulgadas, y el cambio en el ángulo de la llanta es\(\dfrac{\pi}{2}\) radianes, ¿hasta dónde se movió la llanta?
Solución
Dado que la distancia que movió la llanta es igual a la longitud del arco que rodó la llanta, puede usar la ecuación s=r\ theta para determinar hasta dónde llegó la llanta:
\(\begin{aligned} s&=r\theta \\ s&=(14)\left(\dfrac{\pi}{2}\right) \\ s&=7\pi \\ s&\approx 21.98 \text{ in}\end{aligned}\)
Si un objeto con un radio de 10 cm gira para que su arco cubra 54 cm, ¿cuál es el cambio de ángulo del objeto?
Solución
De nuevo puedes usar la ecuación\(s=r\theta \) para resolver este problema:
\(\begin{aligned} s&=r\theta \\ \theta &=\dfrac{s}{r}=\dfrac{54}{10}=5.4 \end{aligned}\)
El disco mueve 5.4 radianes, lo que es un poco menor que una rotación completa, ya que una rotación completa es de aproximadamente 6.28 radianes.
Si tu DVD tiene un radio de 4.5 pulgadas, ¿hasta dónde gira un punto en el disco si el reproductor lo gira\ dfrac {\ pi} {2} radianes?
Solución
Usando\(s=r\theta \),
\(\begin{aligned} s&=r\theta \\ s&=(4.5)\left(\dfrac{\pi }{2}\right) \\ s&=2.25\pi \approx 7.065\end{aligned}\)
Un punto en el disco gira 7.065 pulgadas.
Revisar
El radio de un carrusel es de 8 metros. Utilice esta información para responder a las preguntas 1-3.
- Estás a mitad de camino alrededor del carrusel. ¿Qué tan lejos viajaste?
- Estás todo el camino alrededor del carrusel. ¿Qué tan lejos viajaste?
- Ahora has viajado por todo el carrusel dos veces. ¿Qué tan lejos viajaste?
Una pizza tiene un radio de 10 pulgadas. Utilice esta información para responder preguntas 4-6.
- Se retira una rebanada. La longitud de la corteza de la rebanada faltante es de 3 pulgadas. ¿Cuál es el ángulo central de la rebanada faltante?
- Comes tres piezas con un ángulo central de\(\dfrac{4\pi }{5}\). ¿Cuál es la longitud de la corteza que comió?
- Una pizza grande tiene un radio de 12 pulgadas. ¿Cuál es la longitud de la corteza de la mitad de la pizza grande?
El diámetro de una llanta es de 35 pulg. Utilice esta información para responder a las preguntas 7-10.
- ¿Cuál es la longitud alrededor de toda la llanta?
- La llanta recorre una milla (5280 pies). ¿Cuántas revoluciones hizo la llanta?
- Enrolla la llanta para que gire\(7\pi \) radianes. ¿Qué tan lejos se movió?
- La llanta recorre media milla. ¿Cuántos radianes giró la llanta?
Considera un reloj estándar de 12 horas como el de abajo con un radio de 5 pulgadas. Utilice esto para responder a las preguntas 11-15.
- ¿Cuál es la longitud del arco entre el 3 y el 7?
- ¿Cuál es la longitud del arco entre el 3 y el 2?
- Son las 12:30. ¿Cuál es la longitud del arco entre las manecillas de minutos y horas?
- Son las 7:20. ¿Cuál es la longitud del arco entre las manecillas de minutos y horas?
- Es 1:25. ¿Cuál es la longitud del arco entre las manecillas de minutos y horas?
Reseña (Respuestas)
Para ver la Revisión, abra este archivo PDF y busque la sección 2.5.
El vocabulario
| Término | Definición |
|---|---|
| Arc | Un arco es una sección de la circunferencia de un círculo. |
Recursos adicionales
Video: Longitud de Arco, Área de Sector, Velocidad Lineal y Velocidad Angular - Ejemplo 5
Práctica: Longitud de un arco

