2.5.5: Velocidad angular
- Page ID
- 107677
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Conversión entre velocidades lineales y angulares usando radio y circunferencia.
Para encontrar una canción en particular en tu reproductor MP3/MP4, puedes usar una rueda de desplazamiento. Esto implica mover el dedo alrededor de la rueda en un movimiento circular. Desafortunadamente para ti, la canción que quieres está cerca del final de tu lista de canciones. Dado que estos reproductores multimedia a menudo pueden contener más de 1,000 canciones, ¡tienes que desplazarte rápido! A medida que mueve el dedo en un círculo, tal vez se pregunte si podría medir qué tan rápido está cubriendo su dedo la distancia alrededor del círculo.
Al observar tu dedo, te das cuenta de que tu dedo se mueve alrededor del círculo dos veces por segundo. Si el radio de la rueda de desplazamiento es de 2 cm, ¿cuál es la velocidad angular de tu dedo a medida que te desplazas por tu lista de canciones? ¿Cuál es la velocidad lineal?
Es posible que ya estés familiarizado con la medición de la velocidad como la relación de la distancia recorrida de un objeto con el tiempo que ha estado en movimiento. No obstante, esta relación es para objetos que se mueven en línea recta. ¿Qué pasa con los objetos que viajan por un camino circular?
¿Recuerdas haber jugado en un tiovivo cuando eras más joven?

Si dos personas están montando en el borde exterior, sus velocidades deberían ser las mismas. Pero, ¿y si una persona está cerca del centro y la otra está al borde? Están en el mismo objeto, pero su velocidad en realidad no es la misma.
Mira el siguiente dibujo.
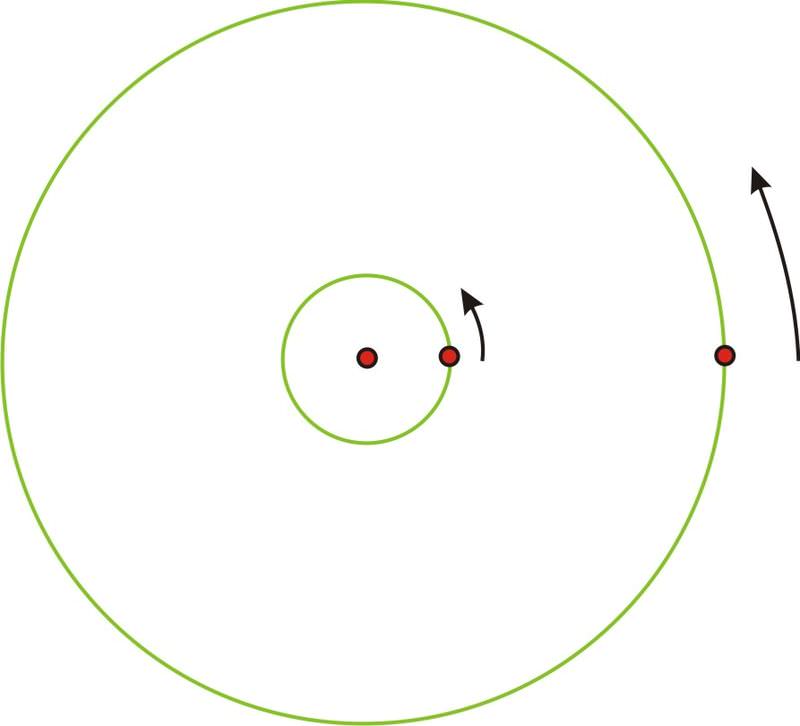
Imagínese que el punto en el círculo más grande es la persona en el borde del tiovivo y el punto en el círculo más pequeño es la persona hacia el medio. Si el tiovivo gira exactamente una vez, entonces ambos individuos también harán una revolución completa en la misma cantidad de tiempo.
No obstante, es obvio que la persona en el centro no viajó tan lejos. La circunferencia (y por supuesto el radio) de ese círculo es mucho menor y por lo tanto la persona que recorrió una distancia mayor en la misma cantidad de tiempo en realidad está viajando más rápido, aunque esté sobre el mismo objeto. Entonces la persona en el borde tiene una mayor velocidad lineal (recordemos que la velocidad lineal se encuentra usando distance=rate ⋅ tiempo). Si alguna vez has montado en un tiovivo, ya lo sabes porque ¡es mucho más divertido estar al borde que en el centro! Pero, hay algo en los dos individuos que viajan alrededor que es lo mismo. Ambos cubrirán la misma rotación en el mismo periodo de tiempo. Este tipo de velocidad, que mide el ángulo de rotación a lo largo de una determinada cantidad de tiempo, se denomina velocidad angular.
La fórmula para la velocidad angular es:
\(\omega =\dfrac{\theta }{t}\)
\(\omega \)es la última letra del alfabeto griego, omega, y se usa comúnmente como símbolo de velocidad angular. \ theta es el ángulo de rotación expresado en medida de radianes, y t es el tiempo para completar la rotación.
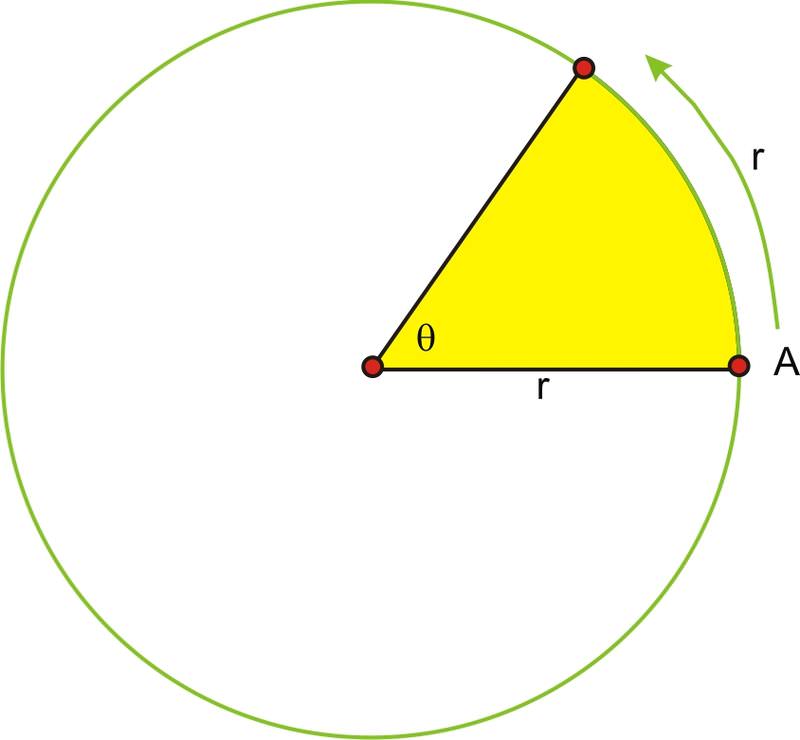
En este dibujo,\(\theta \) es exactamente un radián, o la longitud del radio doblada alrededor del círculo. Si el punto A tardara exactamente 2 segundos en girar a través del ángulo, la velocidad angular de A sería:
\(\begin{aligned} \omega &=\dfrac{\theta }{t}\\ \omega &=\dfrac{1}{2} \text{ radians per second} \end{aligned}\)
Para conocer la velocidad lineal de la partícula, tendríamos que saber la distancia real, es decir, la longitud del radio. Digamos que el radio es de 5 cm.
Si la velocidad lineal es v=dt entonces,\(v=\dfrac{5}{2}\) o\(2.5 \text{ cm per second}\).
Si el ángulo no fuera exactamente de 1 radián, entonces la distancia recorrida por el punto en el círculo es la longitud del arco\(s=r\theta \), o, la longitud del radio por la medida del ángulo en radianes.
Sustituir en la fórmula la velocidad lineal da:\(v=\dfrac{r\theta }{t}\) o\(v=r\cdot \dfrac{\theta }{t}\).
Mira hacia atrás en la fórmula para la velocidad angular. Sustituir\(\omega \) da la siguiente relación entre velocidad lineal y angular,\(v=r\omega \). Entonces, la velocidad lineal es igual al radio multiplicado por la velocidad angular.
Recuerda en un círculo unitario, el radio es de 1 unidad, por lo que en este caso la velocidad lineal es la misma que la velocidad angular.
\(\begin{aligned} v &=r\omega \\ v&=1\times \omega \\ v&=\omega \end{aligned}\)
Aquí, la distancia recorrida alrededor del círculo es la misma para una unidad de tiempo dada que el ángulo de rotación, medido en radianes.
Cálculo de la velocidad lineal y angular
1. Lindsay y Megan están montando en un tiovivo. Megan está de pie a 2.5 pies del centro y Lindsay está montando en el borde exterior a 7 pies del centro. Les toma 6 segundos completar una rotación. Calcular la velocidad lineal y angular de cada niña.
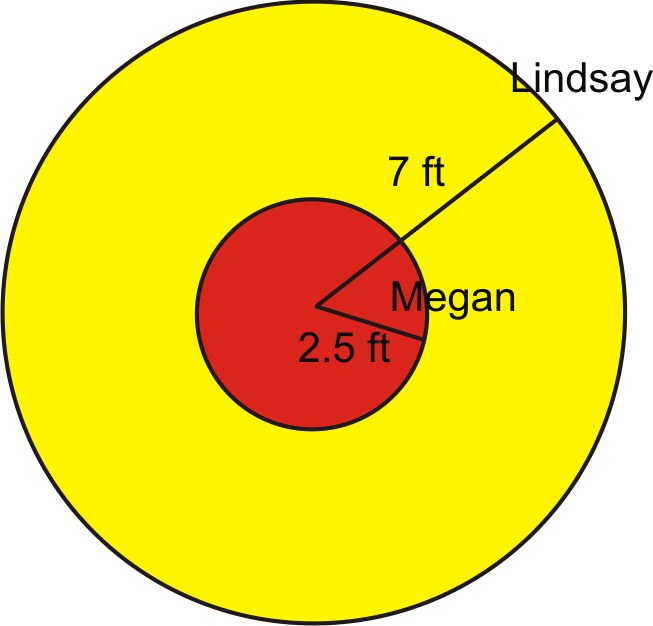
Nos dicen que se necesitan 6 segundos para completar una rotación. Una rotación completa es lo mismo que\(2\pi \) los radianes. Entonces la velocidad angular es:
\(\omega =\dfrac{\theta }{t}=\dfrac{2\pi }{6}=\dfrac{\pi }{3}\)radianes por segundo, que es un poco más de 1 (aproximadamente 1.05), radianes por segundo. Debido a que ambas chicas cubren el mismo ángulo de rotación en la misma cantidad de tiempo, su velocidad angular es la misma. En este caso rotan aproximadamente 60 grados del círculo cada segundo.
Como comentamos anteriormente, sus velocidades lineales son diferentes. Usando la fórmula, la velocidad lineal de Megan es:
\(v=r\omega =(2.5)\left(\dfrac{\pi }{3}\right)\approx 2.6 \text{ ft per sec}\)
La velocidad lineal de Lindsay es:
\(v=r\omega =(7)\left(\dfrac{\pi }{3}\right)\approx 7.3 \text{ ft per sec}\)
2. Un bicho está parado cerca del borde exterior de un disco compacto (de manera que su radio desde el centro del disco es de 6 cm) que está girando. Se da cuenta de que ha viajado\(\pi \) radianes en dos segundos. ¿Cuál es su velocidad angular? ¿Cuál es su velocidad lineal?

Sabemos que la ecuación para la velocidad angular es
\(\omega =\dfrac{\theta }{t}=\dfrac{\pi }{2} \text{ radians per second}\).
Podemos usar la ecuación dada para encontrar su velocidad lineal:
\(v=r\omega =(6)(\dfrac{\pi }{2})\approx 9.42 \text{ cm per sec}\)
Resolviendo valores desconocidos
¿Cuánto tiempo tarda el error en el problema anterior en pasar por dos turnos completos?
Dado que la velocidad angular del error es\(\dfrac{\pi }{2}\) radianes por segundo, podemos usar la ecuación para velocidad angular y resolver por tiempo:
\(\begin{aligned} \omega &=\dfrac{\theta }{t} \\ t&=\theta \omega \end{aligned}\)
Como hay\(4\pi \) radianes en dos vueltas completas del disco, podemos usar esto para el valor de\ theta:
\(t=\dfrac{4\pi }{\dfrac{\pi }{2}}=4\pi \times \dfrac{2}{\pi} =8 \text{ seconds}\)
Anteriormente, se le pidió que encontrara la velocidad angular y lineal de su dedo.
Solución
Como descubriste en esta sección, la velocidad angular es el cambio de ángulo dividido por el cambio en el tiempo. Como barres alrededor del círculo dos veces en un segundo, esto se convierte en:
\(\omega =\dfrac{4\pi }{1}=4\pi \text{ rad/sec}\)
Además, puede encontrar la velocidad lineal con la ecuación:
\(v=r\omega =(2)(4\pi )=8\pi \approx 25.132 \text{ cm/s}\)
Doris y Lois van a dar un paseo en un carrusel. Doris monta en uno de los caballos exteriores y Lois cabalga en uno de los caballos más pequeños cerca del centro. El caballo de Lois está a 3 m del centro del carrusel, y el caballo de Doris está a 7 m más lejos del centro que el de Lois. Cuando se inicia el carrusel, les toma 12 segundos completar una rotación.
Calcular la velocidad lineal de cada niña. Calcular la velocidad angular de los caballos en el carrusel.
Solución
En realidad, es más fácil calcular primero la velocidad angular. \(\omega =\dfrac{2\pi }{12}=\dfrac{\pi }{6}\), entonces la velocidad angular es\(\dfrac{\pi }{6}\) rad, o\(0.524\). Debido a que la velocidad lineal depende del radio, cada niña tiene la suya propia.
Lois:\(v=r\omega =3\cdot \dfrac{\pi }{6}=\dfrac{\pi }{2}\) o\(1.57 \text{ m/sec}\)
Doris:\(v=r\omega =10\cdot \dfrac{\pi }{6}=\dfrac{5 \pi }{3}\) o\(5.24 \text{ m/sec}\)
El Gran Colisionador de Hadrones cerca de Ginebra, Suiza, comenzó a operar en 2008 y está diseñado para realizar experimentos que los físicos esperan que proporcionen información importante sobre la estructura subyacente del universo. El LHC es circular con una circunferencia aproximada de 27,000 m. Los protones se acelerarán a una velocidad muy cercana a la velocidad de la luz (\(\approx 3\times 10^8\)metros por segundo).
¿Cuánto tiempo tarda un protón en hacer una rotación completa alrededor del colisionador? ¿Cuál es la velocidad angular aproximada (al metro por segundo más cercano) de un protón que viaja alrededor del colisionador? Aproximadamente, ¿cuántas veces viajaría un protón alrededor del colisionador en un segundo completo?
Solución
\(v=\dfrac{d}{t}\rightarrow 3\times 10^8=\dfrac{27,000}{t} \rightarrow t= \dfrac{2.7\times 10^4}{3\times 10^8}=0.9\times 10^{−4}=9\times 10^{−5} \text{ or } 0.00009 \text{ seconds}\)
\(\omega =\dfrac{\theta }{t}=\dfrac{2\pi }{0.00009}\approx 69,813 \text{ rad/sec}\)
El protón gira una vez en 0.00009 segundos. Entonces, en un segundo rotará alrededor de los\(1\div 0.00009=11,111.11\) tiempos del LHC, o poco más de 11,111 rotaciones.
Ted está parado a 2 metros del centro de una alegre vuelta. Si su velocidad lineal es de 6 m/s, ¿cuál es su velocidad angular?
Solución
Dado que la ecuación que relaciona la velocidad lineal y angular viene dada por\(v=r\omega \), podemos resolver para omega:\(\omega =\dfrac{v}{r}=\dfrac{6}{2}=3\)
Revisar
Beth y Steve están en un carrusel. Beth está a 7 pies del centro y Steve está justo en el borde, 7 pies más lejos del centro que Beth. Utilice esta información y la siguiente imagen para responder a las preguntas 1-6.
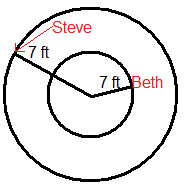
- El carrusel hace una revolución completa en 12 segundos. ¿Hasta dónde llegó Beth en una revolución? ¿Hasta dónde llegó Steve en una revolución?
- Si el carrusel continúa haciendo revoluciones cada 12 segundos, ¿cuál es la velocidad angular del carrusel?
- ¿Cuáles son las velocidades lineales de Beth y Steve?
- Qué tan lejos del centro tendría que estar Beth para tener una velocidad lineal de\(\pi \) pies por segundo.
- El carrusel cambia a una nueva velocidad angular de\(\dfrac{\pi }{3}\) radianes por segundo. ¿Cuánto tiempo se tarda en hacer una revolución completa ahora?
- Con la nueva velocidad del carrusel, ¿cuáles son las nuevas velocidades lineales de Beth y Steve?
- Beth y Steve van en otro carrusel que tiene una velocidad angular de\(\dfrac{\pi }{8}\) radianes por segundo. La velocidad lineal de Beth es\(2\pi\) pies por segundo. ¿A qué distancia está parada del centro del carrusel?
- La velocidad lineal de Steve es de sólo\(\dfrac{\pi }{3}\) pies por segundo. ¿A qué distancia está parado del centro del carrusel?
- ¿Cuál es la velocidad angular de la manecilla de minutos en un reloj? (en radianes por minuto)
- ¿Cuál es la velocidad angular de la manecilla de las horas en un reloj? (en radianes por minuto)
- Un cierto reloj tiene un radio de 1 pie. ¿Cuál es la velocidad lineal de la punta del minutero?
- En el mismo reloj, ¿cuál es la velocidad lineal de la punta de la manecilla de las horas?
- La punta de la manecilla de minutos en otro reloj tiene una velocidad lineal de 2 pulgadas por minuto. ¿Cuál es el radio del reloj?
- ¿Cuál es la velocidad angular del segundero en un reloj? (en radianes por minuto)
- La punta de la segunda manecilla sobre un reloj tiene una velocidad lineal de 2 pies por minuto. ¿Cuál es el radio del reloj?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.8.
El vocabulario
| Término | Definición |
|---|---|
| velocidad angular | La velocidad angular es la relación de revoluciones que ocurren por unidad de tiempo. |
| Velocidad Angular | La velocidad angular de un objeto giratorio es el cambio en el ángulo de un objeto dividido por el cambio en el tiempo. |
| análisis dimensional | El análisis dimensional es un proceso para convertir de una unidad a otra. |
| velocidad lineal | La velocidad lineal es la relación de distancia por unidad de tiempo. |
| Velocidad Lineal | La velocidad lineal de un objeto es el cambio de posición de un objeto dividido por el cambio en el tiempo. |
| radián | Un radián es una unidad de ángulo que es igual al ángulo creado en el centro de un círculo cuyo arco es igual en longitud al radio. |
Recursos adicionales
Video: Velocidad lineal y velocidad angular
Práctica: Velocidad angular
Mundo Real: Construyendo Momentum

