4.1.4: Triángulos ángulo-Lado
- Page ID
- 107607
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ley de los senos dada dos ángulos y el lado incluido.
Estás almorzando en la cafetería una tarde mientras trabajas en tus tareas de matemáticas. Últimamente parece notar las formas triangulares en todo. En casa, en la escuela, con tus amigos. Parece que los triángulos están por todas partes. Y te encuentras tratando de aplicar lo que estás aprendiendo en clase de matemáticas a todos los triángulos que te rodean. Y hoy no es la excepción. A medida que empiezas a morderte tu chip, de repente reconoces esa forma familiar: el triángulo.
Se estima que la longitud de uno de los lados de la viruta es de 3 cm. También se puede decir que el ángulo adyacente al lado de 3 cm es\(50^{\circ} \) y el ángulo adyacente en el otro lado del borde de 3 cm es\(60^{\circ} \). ¿Puedes encontrar las longitudes de los otros dos lados usando técnicas de tu clase de matemáticas?
Triángulos ASA
La Ley de Sines establece:\(\dfrac{\sin A}{a}=\dfrac{\sin B}{b}\). Esta es una relación entre el seno de un ángulo en un triángulo y la longitud del lado opuesto a ese ángulo al seno de un ángulo diferente en ese triángulo y la longitud del lado opuesto a ese segundo ángulo.
Un caso en el que utilizamos la Ley de Sines es cuando conocemos dos ángulos en un triángulo y el lado incluido (ASA). Por ejemplo, en\(\Delta TRI\):
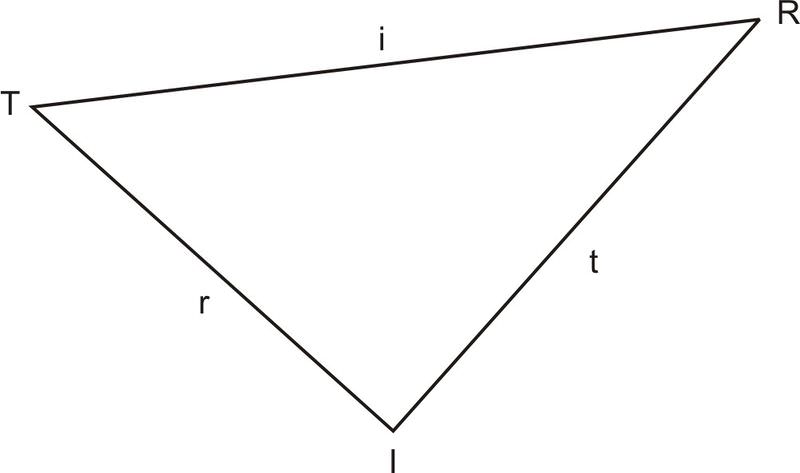
\(\angle T\),\(\angle R\), y\(i\) son conocidos
\(\angle T\),\(\angle I\), y\(r\) son conocidos
\(\angle R\),\(\angle I\), y\(t\) son conocidos
En este caso, la Ley de Sines nos permite encontrar cualquiera de los lados no incluidos.
Uso de la Ley de los Sines
1. En el triángulo de arriba,\(\Delta TRI\),\(\angle T=83^{\circ} \),\(\angle R=24^{\circ} \), y\(i=18.5\). Encuentra la medida de\(t\).
Ya que conocemos dos ángulos y el lado incluido, podemos encontrar cualquiera de los lados no incluidos utilizando la Ley de Sines. Como ya conocemos dos de los ángulos en el triángulo, podemos encontrar el tercer ángulo usando el hecho de que la suma de todos los ángulos en un triángulo debe ser igual\(180^{\circ} \).
\(\begin{aligned} \angle I&=180−(83+24) \\ \angle I&=180−107 \\ \angle I&=73^{\circ} \end{aligned}\)
Ahora que sabemos\(\angle I=73^{\circ} \), podemos usar la Ley de los Sinos para encontrar\(t\).
\(\begin{aligned} \dfrac{\sin 73}{18.5}&=\dfrac{\sin 83}{t} \\ t(\sin 73)&=18.5(\sin 83) \\ t&=\dfrac{18.5(\sin 83)}{\sin 73} \\ t&\approx 19.2 \end{aligned}\)
Observe cómo esperamos hasta el último paso para ingresar los valores en la calculadora. Esto es para que nuestra respuesta sea lo más precisa posible.
2. Para evitar una gran y peligrosa tormenta de nieve en un vuelo de Chicago a Búfalo, el piloto John comienza\(27^{\circ} \) fuera de la trayectoria de vuelo normal. Después de volar 412 millas en esta dirección, gira el avión hacia Búfalo. El ángulo formado por el primer curso de vuelo y el segundo curso de vuelo es\(88^{\circ} \). Para el piloto, son apremiantes dos temas:
- ¿Cuál es la distancia total de la trayectoria de vuelo modificada?
- ¿Cuánto más viajó que si se hubiera quedado en rumbo?
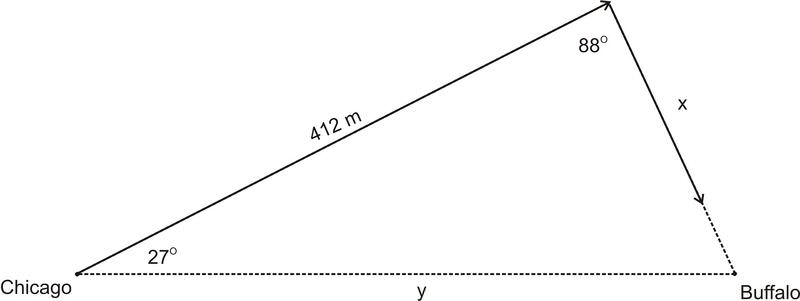
Para poder encontrar la distancia total de la trayectoria de vuelo modificada, necesitamos saber lado\(x\). Para encontrar lado\(x\), necesitaremos usar la Ley de los Sinos. Ya que conocemos dos ángulos y el lado incluido, este es un caso ASA. Recuerda que en el caso ASA, primero tenemos que encontrar el tercer ángulo en el triángulo.
\(\begin{aligned} \text{Missing Angle}&=180−(27+88)=65^{\circ} && \text{The sum of angles in a triangle is 180} \\ \dfrac{\sin 65}{412}&=\dfrac{\sin 27}{x} && \text{Law of Sines} \\ x(\sin 65)&=412(\sin 27) && \text{Cross multiply}\\ x&=\dfrac{412(\sin 27)}{\sin 65} && \text{ Divide by} \sin 65 \\ x &\approx 206.4 \text{ miles} \end{aligned}\)
La distancia total de la trayectoria de vuelo modificada es\(412+206.4=618.4 \text{ miles}\).
Para saber cuánto más lejos tuvo que viajar John, necesitamos saber la distancia de la ruta de vuelo original,\(y\). Podemos volver a utilizar la Ley de los Sinos para encontrar\(y\).
\(\begin{aligned}\dfrac{\sin 65}{412}&=\dfrac{\sin 88}{y} && \text{Law of Sines}\\ y(\sin 65)&=412(\sin 88) && \text{Cross multiply}\\ y&=\dfrac{412(\sin 88)}{\sin 65} && \text{Divide by }\sin 65\\ y &\approx 454.3 \text{ miles} \end{aligned}\)
John tuvo que viajar\(618.4−454.3=164.1 \text{ miles}\) más lejos.
2. En el triángulo que se muestra aquí:
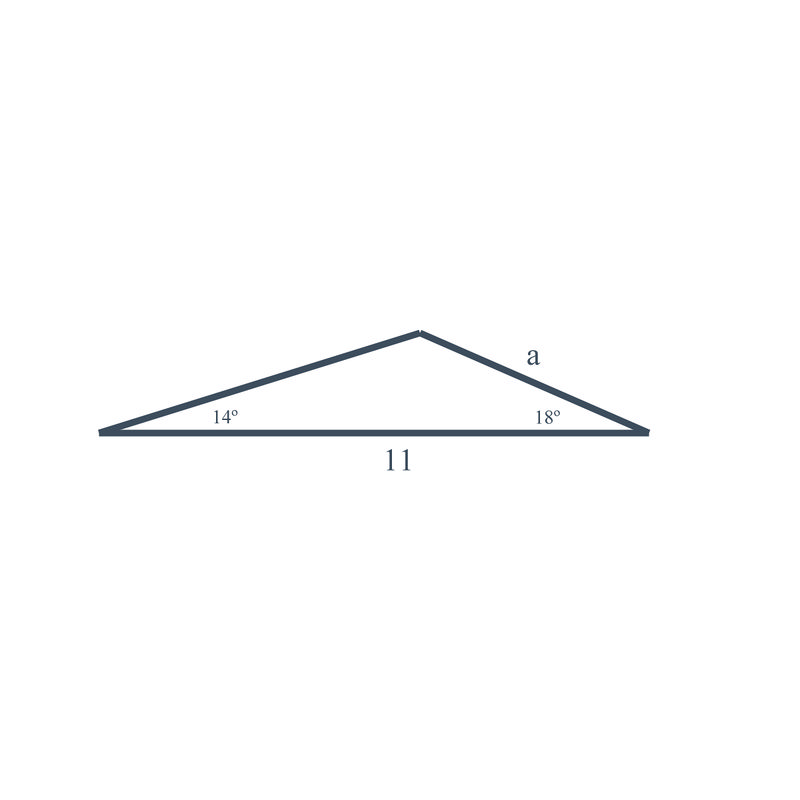
Los lados dados son\(\angle A=14^{\circ} \),\(\angle B=18^{\circ} \), y\(c = 11\). Encuentra la longitud del lado “a”.
Ya que conocemos dos ángulos y el lado incluido, podemos encontrar cualquiera de los lados no incluidos utilizando la Ley de Sines. Como ya conocemos dos de los ángulos en el triángulo, podemos encontrar el tercer ángulo usando el hecho de que la suma de todos los ángulos en un triángulo debe ser igual\(180^{\circ} \).
\(\begin{aligned} \angle C &=180−(18+14)\\ \angle C &=180−32\\ \angle C&=148^{\circ} \end{aligned}\)
Usa la Ley de Sines para encontrar la longitud del lado “a”:
\(\begin{aligned} \dfrac{\sin 14}{a}&=\dfrac{\sin 148}{11} \\ 11(\sin 14)&=a(\sin 148) \\ a&=\dfrac{11(\sin 14)}{\sin 148} \\ a &\approx 5.02 \end{aligned}\)
Anteriormente, se le pidió que encontrara las otras dos longitudes del triángulo.
Solución
Puedes usar la Ley de Sines para encontrar la longitud de cualquiera de los otros 2 lados. No obstante, primero es bueno señalar que dado que la suma de los ángulos interiores de un triángulo debe ser igual\(180^{\circ} \), el tercer ángulo en el triángulo debe medir\(180^{\circ} −50^{\circ} −60^{\circ} =70^{\circ} \).
Ahora para configurar los ratios:
\(\begin{aligned} \dfrac{\sin 60}{a}&=\dfrac{\sin 70}{3} \\ 3(\sin 60)&=a(\sin 70) \\ a&=\dfrac{3(\sin 60)}{\sin 70} \\ a&\approx 2.7647 \end{aligned}\)
La longitud de uno de los otros 2 lados es de aproximadamente 2.7647 centímetros.
Para encontrar la longitud del último lado:
\(\begin{aligned} \dfrac{\sin 50}{b}&=\dfrac{\sin 70}{3} \\ 3(\sin 50)&=b(\sin 70) \\ b&=\dfrac{3(\sin 50)}{\sin 70} \\ b &\approx 2.46 \end{aligned}\)
La longitud del otro de los 2 lados desconocidos es de aproximadamente 2.46 centímetros.
Encuentra el lado “a” en el triángulo de abajo usando la siguiente información:\(b=16,\; A=11.7^{\circ} ,\; C=23.8^{\circ}\)
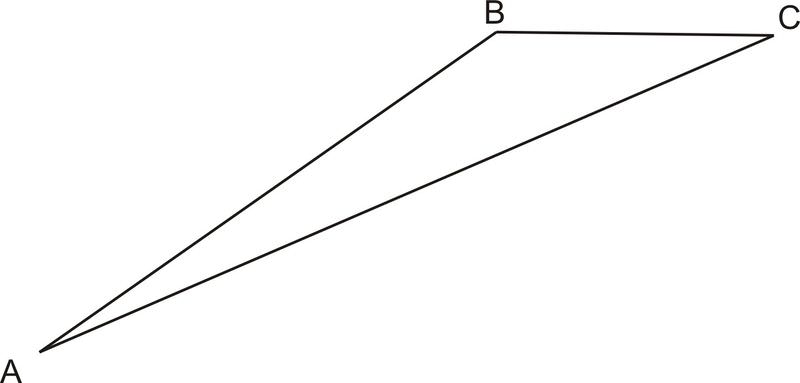
Solución
\(\dfrac{\sin 11.7^{\circ} }{a}=\dfrac{\sin 144.5^{\circ} }{16},\; a=5.6\)
Encuentra el lado “a” en el triángulo de abajo usando la siguiente información:\(k=6.3,\; J=16.2^{\circ} ,\; L=40.3^{\circ}\)
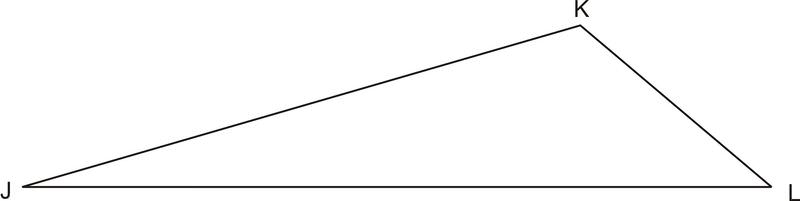
Solución
\(\dfrac{\sin 40.3^{\circ} }{l}=\dfrac{\sin 123.5^{\circ} }{6.3} ,\; l=4.9\)
A pesar de que los triángulos ASA y AAS representan dos casos distintos de la Ley de los Sines, ¿qué tienen en común ambos?
Solución
Las respuestas de los estudiantes variarán pero deben notar que en ambos casos conoces o puedes encontrar un ángulo y el lado frente a él.
Revisar
En\(\Delta ABC\),\(m\angle A=40^{\circ} \),\(m\angle B=67^{\circ} \), y\(c = 6\).
- Encuentra\(m\angle C\).
- Encuentra la longitud de\(a\).
- Encuentra la longitud de\(b\).
En\(\Delta DEF\),\(m\angle D=36^{\circ} \),\(m\angle E=101^{\circ} \), y\(f = 11\).
- Encuentra\(m\angle F\).
- Encuentra la longitud de\(d\).
- Encuentra la longitud de\(e\).
En\(\Delta BIG\),\(m\angle B=56^{\circ} \),\(m\angle I=71^{\circ} \), y\(g = 23\).
- Encuentra\(m\angle G\).
- Encuentra la longitud de\(b\).
- Encuentra la longitud de\(i\).
En\(\Delta APL\),\(m\angle A=79^{\circ} \),\(m\angle P=40^{\circ} \), y\(l = 15\).
- Encuentra\(m\angle L\).
- Encuentra la longitud de\(a\).
- Encuentra la longitud de\(p\).
En\(\Delta SAU\),\(m\angle S=5^{\circ} \),\(m\angle A=99^{\circ} \), y\(u = 21\).
- Encuentra\(m\angle U\).
- Encuentra la longitud de\(s\).
- Encuentra la longitud de\(a\).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.8.
El vocabulario
| Término | Definición |
|---|---|
| Ángulo Ángulo Lateral Triángulo | El término 'triángulo ángulo-lado-ángulo' se refiere a un triángulo con medidas conocidas de dos ángulos y la longitud del lado entre ellos. |
Recursos adicionales
Video: Ley de los Senos - Resolviendo Triángulo ASA
Práctica: Triángulos de ángulo lateral

