4.2.2: Introducción a la fórmula del área del triángulo
- Page ID
- 107629
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Encuentra áreas de triángulos no rectos usando la relación sinusoidal
Mientras estás en el comedor con tus amigos algún día, estás discutiendo diferentes formas de usar las cosas que has aprendido en la clase de matemáticas. Le dices a tus amigos que has estado aprendiendo mucho sobre los triángulos, como cómo encontrar su área. Uno de tus amigos mira tu plato y empieza a sonreír.
“Muy bien”, dice. “Si eres tan bueno en las cosas que involucran triángulos, te reto a encontrar algo sencillo. Dime el área de tu rebanada de pizza”. Apunta hacia abajo a la pizza de tu plato.
La pizza tiene forma de triángulo. Pero desafortunadamente no es un triángulo rectángulo. El borde exterior mide 5 pulgadas de largo y los lados largos son de 7 pulgadas de largo. El ángulo entre el borde y el lado largo de la rebanada es\(69^{\circ} \). ¿Hay alguna manera de decirle el área de tu porción de pizza?
Derivando la fórmula del área del triángulo
Podemos usar la fórmula de área de Geometría,\(A=\dfrac{1}{2} bh\), así como la función seno, para derivar una nueva fórmula que se puede usar cuando se desconoce la altura, o altitud, de un triángulo.
En\(\Delta ABC\) abajo,\(BD\) es altitud de\(B\) a\(AC\). Nos referiremos a la longitud de\(BD\) como\(h\) ya que también representa la altura del triángulo. También, nos referiremos al área del triángulo como\(K\) para evitar confundir el área con\(\angle A\).
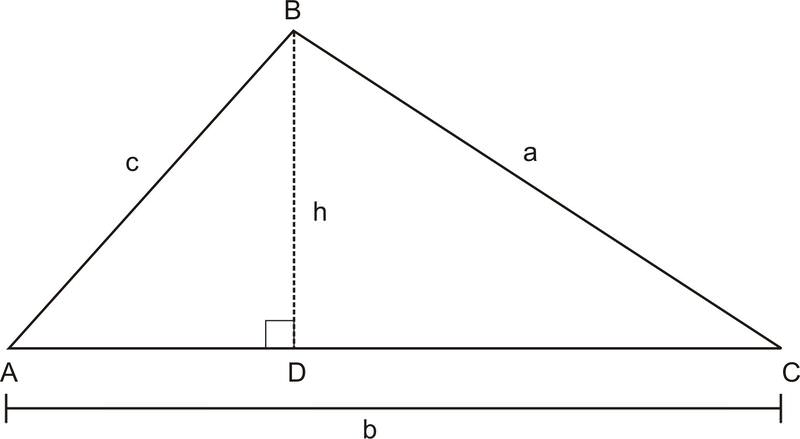
\(\begin{aligned} k &=\dfrac{1}{2} bh && \text{ Area of a triangle } \\ k&=\dfrac{1}{2} b(c \sin A) &&\sin A=\dfrac{h }{c} \text{ therefore } c \sin A=h \\ k&=\dfrac{1}{2} bc \sin A && \text{Simplify} \end{aligned}\)
Podemos usar un método similar para derivar las tres formas de la fórmula de área, independientemente del ángulo:
\(\begin{aligned} K &=\dfrac{1}{2} bc \sin A\\ K&=\dfrac{1}{2} ac \sin B \\ K&=\dfrac{1}{2} ab \sin C \end{aligned}\)
La fórmula\(K=\dfrac{1}{2} bc \sin A\) requiere que conozcamos dos lados y el ángulo incluido (SAS) en un triángulo. Una vez que conocemos estas tres cosas, podemos calcular fácilmente el área de un triángulo oblicuo.
Encontrar el área de un triángulo
1. En\(\Delta ABC\),\(\angle C=62^{\circ} \),\(b=23.9\), y\(a=31.6\). Encuentra el área del triángulo.
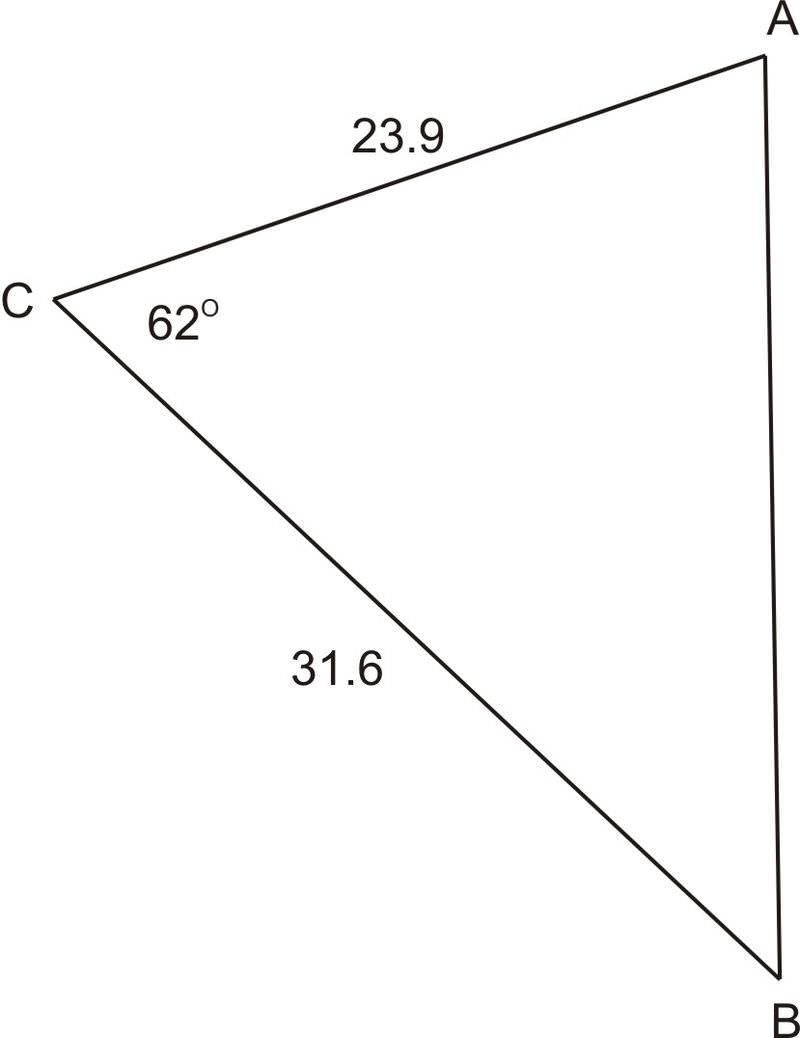
Usando nuestra nueva fórmula,\(K=\dfrac{1}{2} ab\sin C\), enchufa lo que se conoce y resuelve para el área.
\(\begin{aligned} K &=\dfrac{1}{2}(31.6)(23.9)\sin 62 \\ K &\approx 333.4 \end{aligned}\)
2. El Hotel Pyramid instaló recientemente una piscina triangular. Un lado de la piscina es de 24 pies, otro lado es de 26 pies, y el ángulo entre los dos lados es\(87^{\circ} \). Si el gerente del hotel necesita ordenar una cobertura para la piscina, y el costo es\($35\) por pie cuadrado, ¿cuánto puede esperar gastar?
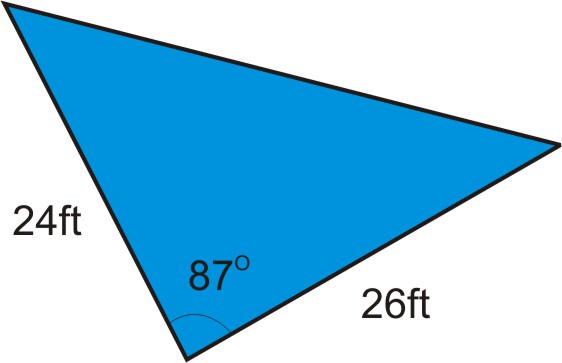
Para encontrar el costo de la cobertura, primero necesitamos conocer el área de la cobertura. Una vez que sepamos cuántos pies cuadrados es la cubierta, podemos calcular el costo. En la ilustración anterior, se puede ver que conocemos dos de los lados y el ángulo incluido. Esto significa que podemos usar la fórmula\(K=\dfrac{1}{2} bc \sin A\).
\(\begin{aligned} K&=\dfrac{1}{2} (24)(26)\sin 87 \\ K&\approx 311.6 \\ 311.6 \text{ sq.ft.} \times $35/ \text{ sq.ft. }&=$10,905.03 \end{aligned}\)
El costo de la cobertura será\($10,905.03\).
3. En\(\Delta GHI\),\(\angle I=15^{\circ} \),\(g=14.2\), y\(h=7.9\). Encuentra el área del triángulo.
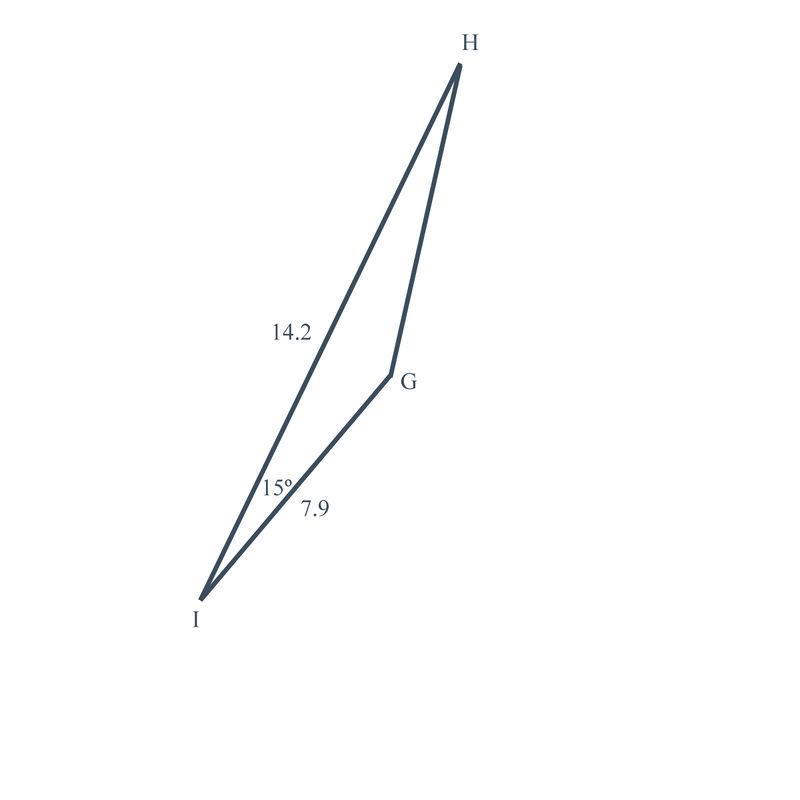
Usando nuestra nueva fórmula\(K=\dfrac{1}{2} ab \sin C\), que es la misma que\(K=\dfrac{1}{2} gh \sin I\), enchufa lo que se conoce y resuelve para la zona.
\(\begin{aligned} K &=\dfrac{1}{2} (14.2)(7.9)\sin 15 \\ K&\approx 14.52\end{aligned} \)
Anteriormente, se le preguntó si había alguna manera de decirle el área de su porción de pizza.
Solución
Usa la fórmula\(K=\dfrac{1}{2} bc \sin A\)
donde en este caso, uno de los lados es igual a 5, el otro es igual a 7, y el ángulo es\(69^{\circ} \).
\(K=\dfrac{1}{2} (5)(7) \sin 69^{\circ} =16.34\text{ in}^2\)
Un agricultor necesita replantar una sección triangular de cultivos que murió inesperadamente. Un lado del triángulo mide 186 yardas, otro mide 205 yardas, y el ángulo formado por estos dos lados es\(148^{\circ} \).
¿Cuál es el área de la sección de cultivos que necesita ser replantada?
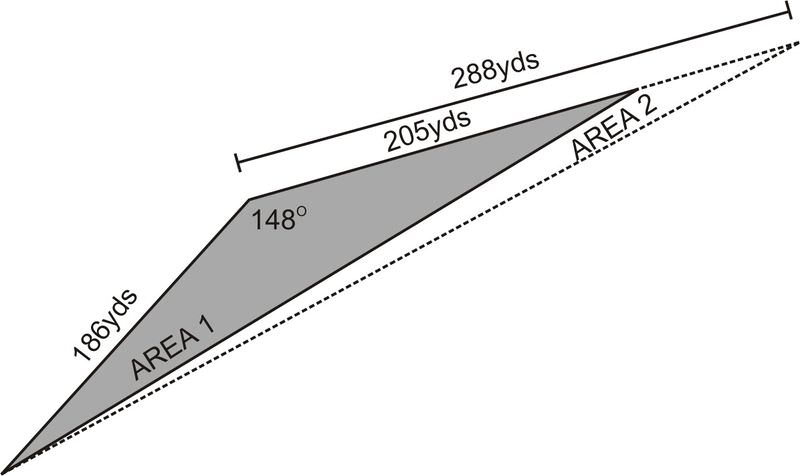
Solución
Uso\(K=\dfrac{1}{2} bc \sin A\),\(K=\dfrac{1}{2} (186)(205)\sin 148^{\circ} \). Entonces, el área que necesita ser reemplazada es de 10102.9 yardas cuadradas.
El agricultor sale unos días después para descubrir que más cultivos han muerto. El lado que solía medir 205 yardas ahora mide 288 yardas. ¿Cuánto ha aumentado el área que necesita ser replantada?
Solución
\(K=\dfrac{1}{2}(186)(288)\sin 148^{\circ} =14193.4\), el área ha aumentado en 4090.5 yardas.
Encuentra el perímetro del cuadrilátero a la izquierda Si el área de\(\Delta DEG=56.5\) y el área de\(\Delta EGF=84.7\).
Solución
Necesitas usar la\(K=\dfrac{1}{2} bc \sin A\) fórmula para encontrar DE y GF.
\(56.5=\dfrac{1}{2} (13.6)DE \sin 39^{\circ} \rightarrow DE=13.2 \qquad 84.7=\dfrac{1}{2}(13.6)EF \sin 60^{\circ} \rightarrow EF=14.4\)
Segundo, es necesario encontrar lados\(DG\) y\(GF\) usar la Ley de Cosinos.
\(\begin{aligned} DG^2 & =13.2^2+13.6^2−2\cdot 13.2\cdot 13.6\cdot \cos 39^{\circ} \rightarrow DG=8.95 \\ GF^2 &=14.4^2+13.6^2−2\cdot 14.4\cdot 13.6\cdot \cos 60^{\circ} \rightarrow GF=14.0 \end{aligned} \)
El perímetro del cuadrilátero es de 50.55.
Revisar
Encuentra el área de cada triángulo.
- \(\Delta ABC\)si\(a=13\),\(b=15\), y\(m\angle C=71^{\circ} \).
- \(\Delta ABC\)si\(b=8\),\(c=4\), y\(m\angle A=67^{\circ} \).
- \(\Delta ABC\)si\(b=34\),\(c=29\), y\(m\angle A=138^{\circ} \).
- \(\Delta ABC\)si\(a=3\),\(b=7\), y\(m\angle C=80^{\circ} \).
- \(\Delta ABC\)si\(a=4.8\),\(c=3.7\), y\(m\angle B=43^{\circ} \).
- \(\Delta ABC\)si\(a=12\),\(b=5\), y\(m\angle C=20^{\circ} \).
- \(\Delta ABC\)si\(a=3\),\(b=10\), y\(m\angle C=50^{\circ} \).
- \(\Delta ABC\)si\(a=5\),\(b=9\), y\(m\angle C=14^{\circ} \).
- \(\Delta ABC\)si\(a=5\),\(b=7\), y\(c=11\).
- \(\Delta ABC\)si\(a=7\),\(b=8\), y\(c=9\).
- \(\Delta ABC\)si\(a=12\),\(b=14\), y\(c=4\).
- Un agricultor mide los tres lados de un campo triangular y obtiene 114, 165 y 257 pies. ¿Cuál es la medida del ángulo más grande del triángulo?
- Utilizando la información del problema anterior, ¿cuál es el área del campo?
Otro campo es un cuadrilátero donde tres lados miden 30, 50 y 60 yardas, y dos ángulos miden\(130^{\circ} \) y\(140^{\circ} \), como se muestra a continuación.
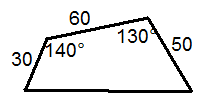
- Encuentra el área del cuadrilátero. Pista: divide el cuadrilátero en dos triángulos y encuentra el área de cada uno.
- Encuentra la longitud del cuarto lado.
- Encuentra las medidas de los otros dos ángulos.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.4.
El vocabulario
| Término | Definición |
|---|---|
| Triángulo oblicuo | Un triángulo oblicuo es un triángulo sin ángulo recto como uno de sus ángulos internos. |
| Triángulo SAS | Un triángulo SAS es un triángulo donde dos lados y el ángulo entre ellos son cantidades conocidas. |
Recursos adicionales
Video: Encontrar el área de un triángulo oblicuo usando la Ley de los Senos - Ejemplo 1

