4.2.3: Determinación de Medidas Triangulares Desconocidas Dada Área
- Page ID
- 107620
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Resuelve partes triangulares faltantes usando fórmulas de área y la ley de cosenos/senos.
Estás trabajando en crear un móvil para tu clase de arte. Un móvil es una obra de arte que tiene una varilla con diferentes formas colgando de él, para que puedan girar.
Para crear tu proyecto, necesitas cortar un conjunto de triángulos que tengan una variedad de tamaños. Estás a punto de empezar a cortar triángulos, cuando tu amigo, que te está ayudando con el proyecto, se acerca. Ella te dice que cada pieza necesita tener una varilla a través del costado de la misma para equilibrar la forma de cierta manera. Ella quiere que hagas una pieza que se vea así:
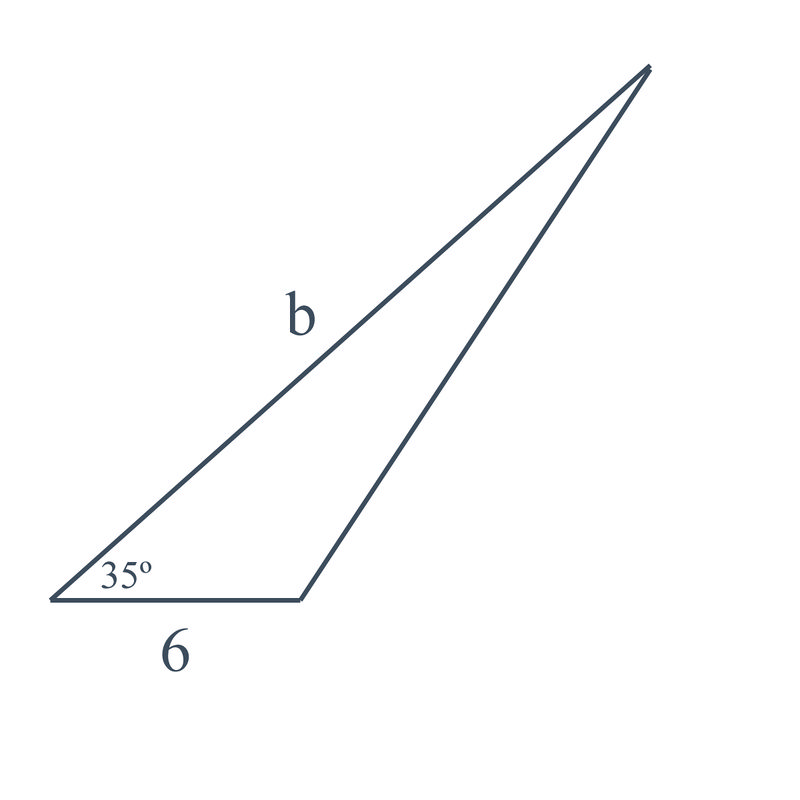
Ya has cortado un triángulo cortando una pieza de papel de construcción. Sabes que un lado de tu triángulo mide 6 pulgadas de largo, pero no sabes la longitud de los otros dos lados. ¿Puedes usar la información que tienes para encontrar la longitud de b en la pieza móvil anterior? (El área del triángulo es\(25\text{ in}^2 \), y el ángulo interior entre el lado de seis pulgadas y el lado que quieres conocer es\(35^{\circ} \)).
Encontrar las medidas de un triángulo dada la zona
En esta sección, veremos situaciones en las que conocemos el área pero necesitamos encontrar otra parte del triángulo, así como una aplicación que involucre un cuadrilátero. Todo ello implicará el uso de la Ley de Cosinos, Ley de Senos, y la Fórmula Alterna para el Área de un Triángulo.
1. El velero de foque en un velero se desató y se perdió la cuerda que la aseguraba. Si el área de la vela de foque es de 56.1 pies cuadrados, use la figura y la información a continuación para encontrar la longitud de la cuerda.
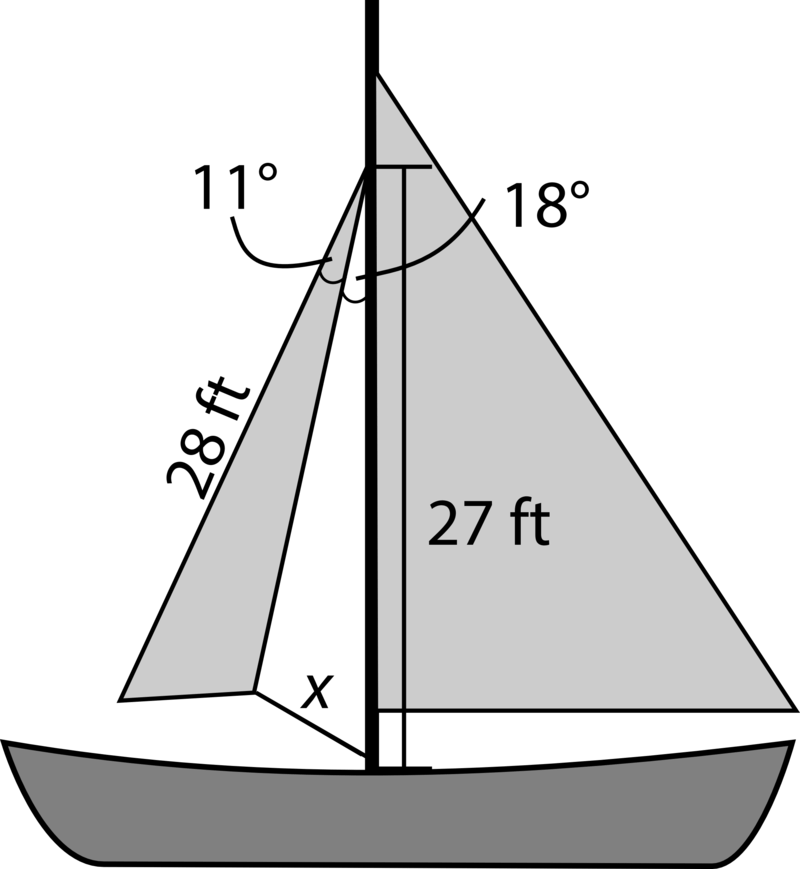
Ya que conocemos el área, uno de los lados, y un ángulo de la vela de foque, podemos usar la fórmula\(K=\dfrac{1}{2} bc \sin A\) para encontrar el lado de la vela de foque que está adherida al mástil. Vamos a llamar a este lado\(y\).
\(\begin{aligned} 56.1 &=\dfrac{1}{2} 28(y)\sin 11\\ 56.1 &=2.671325935 y\\ 21.0&=y \end{aligned}\)
Ahora que conocemos el lado y, conocemos dos lados y el ángulo incluido en el triángulo formado por el mástil, la cuerda y la vela de foque. Ahora podemos usar la Ley de Cosinos para calcular la longitud de la cuerda.
\(\begin{aligned} x^2 &=21^2+27^2−2(21)(27)\cos 18 \\ x^2&=91.50191052 \\ x&\approx 9.6\text{ ft}\end{aligned}\)
La longitud de la cuerda es de aproximadamente 9.6 pies.
2. En cuadrilátero\(QUAD\) abajo, el área de\(\Delta QUD=5.64\), el área de\(\Delta UAD=6.39\),\(\angle QUD=31^{\circ} \),\(\angle DUA=40^{\circ} \), y\(UD=7.8\). Encuentra el perímetro de\(QUAD\).
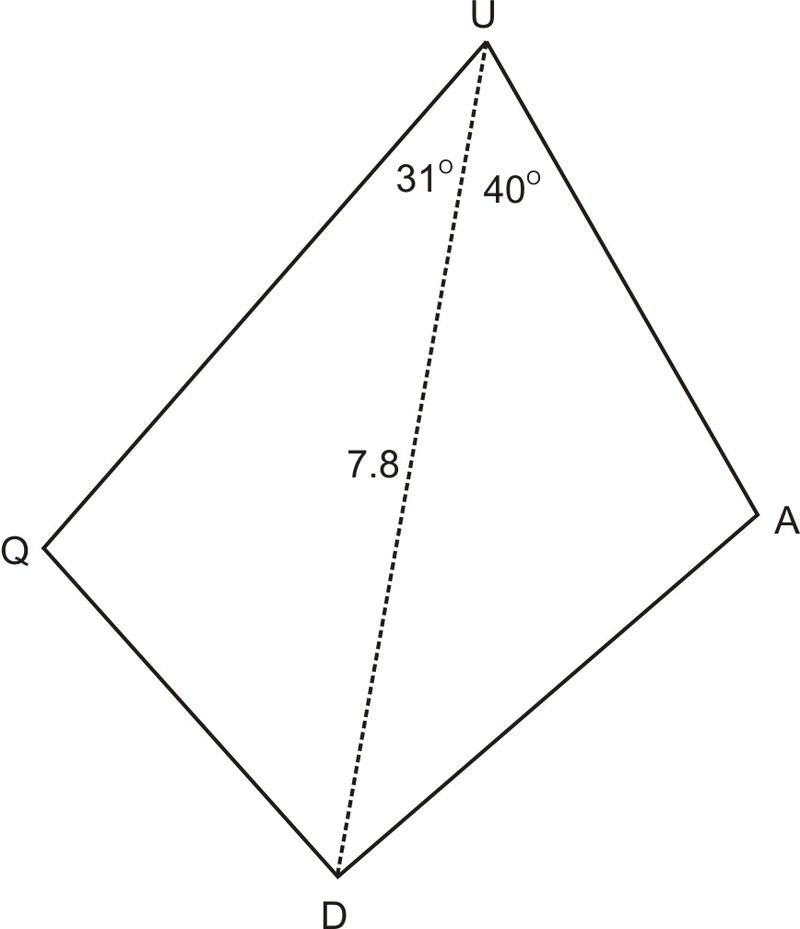
Para poder encontrar el perímetro de\(QUAD\), necesitamos conocer lados\(QU\),\(QD\),\(UA\), y\(AD\). Ya que conocemos el área, un lado, y un ángulo en cada uno de los triángulos, podemos usar\(K=\dfrac{1}{2} bc \sin A\) para averiguar\(QU\) y\(UA\).
\ (\ begin {alineado}
5.64 & =\ dfrac {1} {2} (7.8) (Q U)\ sin 31 & 6.39&=\ dfrac {1} {2} (7.8) U A\ sin 40\
2.8 &\ aprox Q U & 2.5 &\ aprox U A
\ final {alineado}\)
Ahora que conocemos QU y UA, conocemos dos lados y el ángulo incluido en cada triángulo (SAS). Esto significa que podemos usar la Ley de Cosinos para encontrar los otros dos lados, QD y DA. Primero encontraremos QD y DA.
\ (\ begin {alineado}
Q D^ {2} &=2.8^ {2} +7.8^ {2} -2 (2.8) (7.8)\ cos 31 & D A^ {2} &=2.5^ {2} +7.8^ {2} -2 (2.5) (7.8)\ cos 40\\
Q D^ {2} &=31.23893231 & D A^ {2} &=37.21426672\\
Q D&\ aprox 5.6 & D A &\ approx 6.1
\ final {alineado}\)
Finalmente, podemos calcular el perímetro ya que hemos encontrado los cuatro lados del cuadrilátero.
\(pQUAD=2.8+5.6+6.1+2.5=17\)
3. En\(\Delta ABC\),\(BD\) es una altitud de\(B\) a\(AC\). El área de\(\Delta ABC=232.96\),\(AB=16.2\), y\(AD=14.4\). Encuentra\(DC\).
Primero, encuentra BD usando el Teorema de Pitágoras. \(BD=\sqrt{16.2^2−14.4^2}=7.42\). Después, usando el área y fórmula (\(A=\dfrac{1}{2}bh\)), podrás encontrar\(AC\).
\(232.96=\dfrac{1}{2}(7.42)AC\rightarrow AC=62.78. \; DC=62.78−14.4=48.38\).
Anteriormente, se le pidió que encontrara la longitud de\(b\) en la pieza móvil.
Solución
Ya que sabes que la pieza móvil mide seis pulgadas en un lado, y que el área del triángulo es\(25\text{ in}^2 \), puedes usar la fórmula\(K=\dfrac{1}{2} ab \sin C\) para encontrar la longitud del otro lado:
\(\begin{aligned} K&=\dfrac{1}{2} ab \sin C \\ 25&=\dfrac{1}{2} (6)(b)\sin 35^{\circ} \\ 25&=1.72b \\ b&=\dfrac{25}{1.72 }\\ b&=14.53\text{ in}\end{aligned}\)
Encuentra "\(h\)" en el triángulo de abajo:\(\text{Area} =1618.98\),\(b=36.3\)
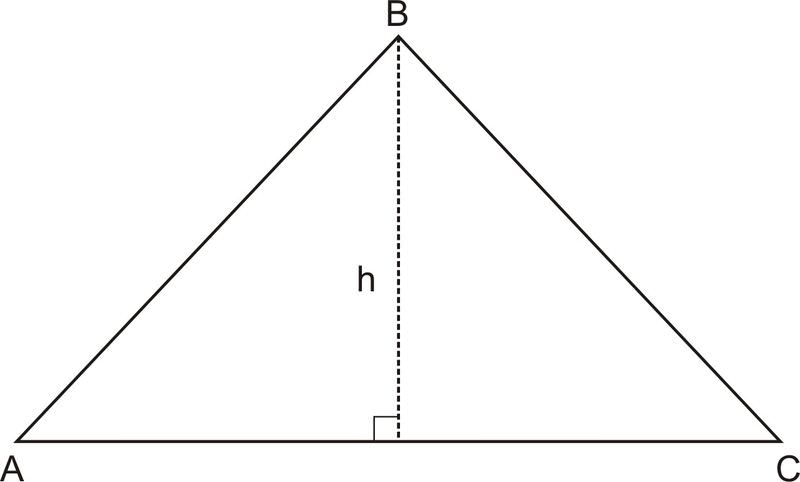
Solución
Ya que conocemos el área, uno de los lados (18.15), y un ángulo del triángulo (\(45^{\circ} \)), podemos usar la fórmula\(K=\dfrac{1}{2} bc \sin A\) para encontrar el otro lado del triángulo. Entonces podemos usar el Teorema de Pitágoras para encontrar la altura del triángulo.
Esto da como resultado:
\(h=89.2\)
Encuentra\(\angle A\) en el triángulo a continuación:\(\text{Area }=387.6\),\(b=25.6\),\(c=32.9\)
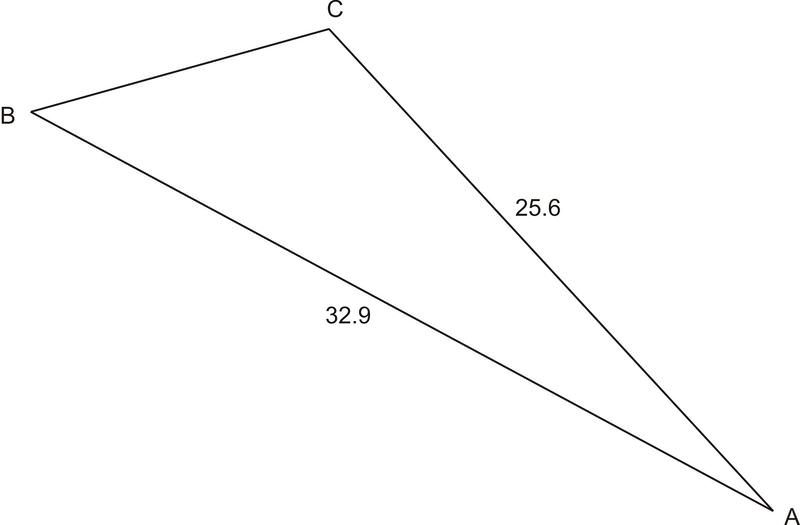
Solución
Ya que conocemos el área y las longitudes de dos de los lados del triángulo, podemos usar la fórmula para resolver\(K=\dfrac{1}{2} bc\sin A\) para el ángulo incluido, lo que da:
\(\angle A=67^{\circ}\)
Encuentra el área de\(\Delta ABC\) abajo:\(\text{Area} \Delta ABD=16.96\),\(AD=3.2\),\(\angle DBC=49.6^{\circ} \)
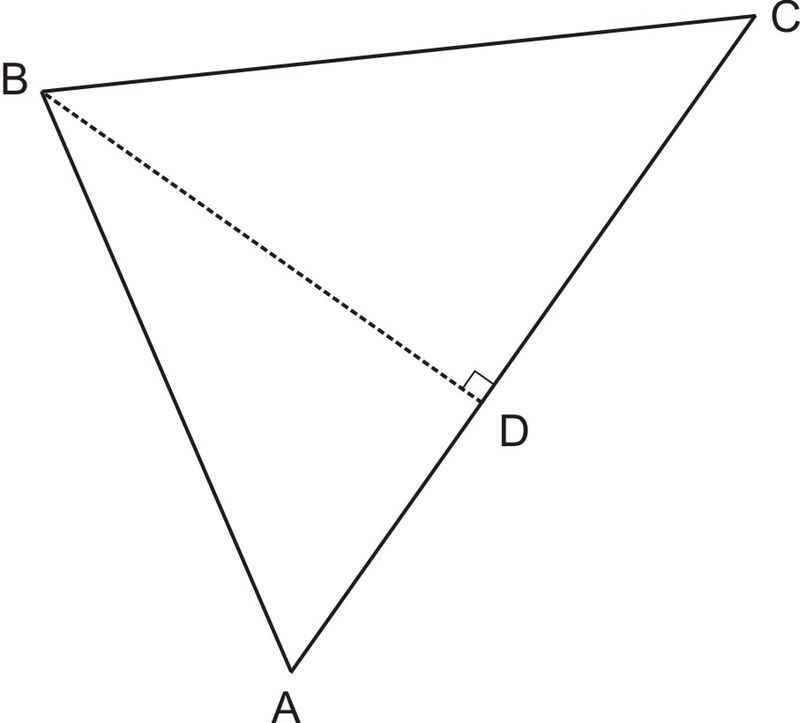
Solución
\(\text{Area of } \Delta ABC=83.0\)
Revisar
- El área del triángulo de abajo es\(138\text{ in}^2 \). Resuelve para\(x\), la altura.
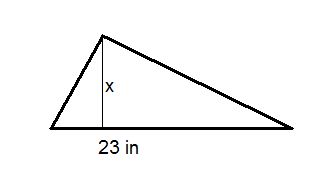
Figura\(\PageIndex{7}\) - El área del triángulo de abajo es\(250\text{ cm}^2 \). Se da una altura en el diagrama. Resolver para\(x\).
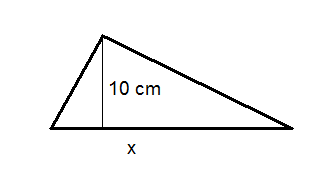
Figura\(\PageIndex{8}\)
Usa el triángulo de abajo para las preguntas 3-5. El área del triángulo grande es\(65 \text{ cm}^2\).
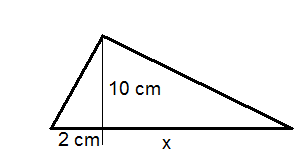
- Resolver para\(x\).
- Encuentra el perímetro del triángulo grande.
- Encuentra la medida de los tres ángulos del triángulo grande.
Utilice el triángulo de abajo para las preguntas 6-8. El área del triángulo es\(244 \text{ cm}^2\).
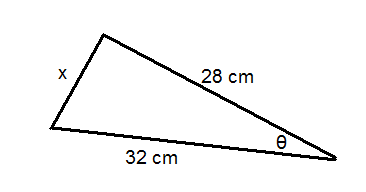
- Resolver para\(\theta \).
- Resolver para\(x\).
- Encuentra el perímetro del triángulo.
Usa el triángulo de abajo para las preguntas 9-11. El área del triángulo es\(299.8 \text{ in}^2\).
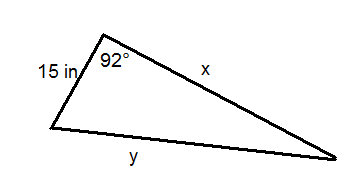
- Resolver para\(x\).
- Resolver para\(y\).
- Encuentra la medida de los otros dos ángulos del triángulo.
Utilice el triángulo de abajo para las preguntas 12-15. El área del triángulo grande es\(84 \text{ in}^2\).
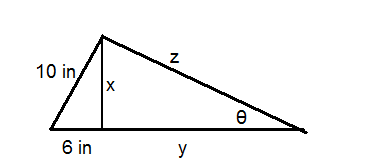
- Resolver para\(x\).
- Resolver para\(y\).
- Resolver para\(z\).
- Resolver para\(\theta \).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.6.
El vocabulario
| Término | Definición |
|---|---|
| ley de cosenos | La ley de los cosenos es una norma que relaciona los lados de un triángulo con el coseno de uno de sus ángulos. La ley de los cosenos establece que\(c^2=a^2+b^2−2ab\cos C\), dónde\(C\) está el ángulo a través de lado\(c\). |
| ley de los senos | La ley de los senos es una regla aplicada a los triángulos que establece que la relación del seno de un ángulo al lado opuesto a ese ángulo es igual a la relación del seno de otro ángulo en el triángulo al lado opuesto a ese ángulo. |

