5.1: Medidas de Tendencia Central
- Page ID
- 151537
Dibujar imágenes de los datos, como hice en la Figura 5.1 es una excelente manera de transmitir la “mesita” de lo que los datos están tratando de decirte, a menudo es extremadamente útil tratar de condensar los datos en unas simples estadísticas de “resumen”. En la mayoría de las situaciones, lo primero que querrás calcular es una medida de tendencia central. Es decir, te gustaría saber algo sobre el “promedio” o “medio” de tus mentiras de datos. Las dos medidas más utilizadas son la media, mediana y modo; ocasionalmente las personas también reportarán una media recortada. Voy a explicar cada uno de estos a su vez, para luego discutir cuándo cada uno de ellos es útil.
media
La media de un conjunto de observaciones es solo una media normal, anticuada: sumar todos los valores hacia arriba, y luego dividir por el número total de valores. Los primeros cinco márgenes de AFL fueron 56, 31, 56, 8 y 32, por lo que la media de estas observaciones es justa:
\ [
\ dfrac {56+31+56+8+32} {5} =\ dfrac {183} {5} =36.60
\ nonumber\]
Por supuesto, esta definición de la media no es noticia para nadie: los promedios (es decir, los medios) se usan tan a menudo en la vida cotidiana que esto es algo bastante familiar. No obstante, dado que el concepto de media es algo que todos ya entienden, voy a usar esto como excusa para comenzar a introducir parte de la notación matemática que utilizan los estadísticos para describir este cálculo, y hablar sobre cómo se harían los cálculos en R.
La primera pieza de notación a introducir es N, que usaremos para referirnos al número de observaciones que estamos promediando (en este caso N=5). A continuación, necesitamos adjuntar una etiqueta a las propias observaciones. Es tradicional usar X para esto, y usar subíndices para indicar de qué observación estamos hablando en realidad. Es decir, usaremos X 1 para referirnos a la primera observación, X 2 para referirnos a la segunda observación, y así sucesivamente, hasta X N para la última. O, para decir lo mismo de una manera un poco más abstracta, usamos X i para referirnos a la i-ésima observación. Solo para asegurarnos de que estamos claros en la notación, la siguiente tabla enumera las 5 observaciones en la variable afl.margins, junto con el símbolo matemático utilizado para referirse a ella, y el valor real al que corresponde la observación:
| La Observación | Su Símbolo | El Valor Observado |
|---|---|---|
| margen ganador, juego 1 | X 1 | 56 puntos |
| margen ganador, juego 2 | X 2 | 31 puntos |
| margen ganador, juego 3 | X 3 | 56 puntos |
| margen ganador, juego 4 | X 4 | 8 puntos |
| margen ganador, juego 5 | X 5 | 32 puntos |
Bien, ahora intentemos escribir una fórmula para la media. Por tradición, usamos x̄ como notación para la media. Por lo que el cálculo de la media podría expresarse usando la siguiente fórmula:
\ [
\ bar {X} =\ dfrac {X_ {1} +X_ {2} +\ lDOTS+x_ {N-1} +X_ {N}} {N}
\ nonumber\]
Esta fórmula es del todo correcta, pero es terriblemente larga, así que hacemos uso del símbolo de suma para acortarla. 65 Si quiero sumar las primeras cinco observaciones, podría escribir la suma el largo camino, X1+X2+X3+X4+X5 o podría usar el símbolo de suma para acortarlo a esto:
\ [
\ suma_ {i=1} ^ {5} X_ {i}
\ nonumber\]
Tomado literalmente, esto podría leerse como “la suma, tomada sobre todos los valores i del 1 al 5, del valor X i”. Pero básicamente, lo que significa es “sumar las cinco primeras observaciones”. En cualquier caso, podemos usar esta notación para escribir la fórmula de la media, que se ve así:
\ [
\ bar {X} =\ dfrac {1} {N}\ suma_ {i=1} ^ {N} X_ {i}
\ nonumber\]
Con toda honestidad, no puedo imaginar que toda esta notación matemática ayude a aclarar en absoluto el concepto de la media. De hecho, en realidad es solo una forma elegante de escribir lo mismo que dije en palabras: sumar todos los valores hacia arriba, y luego dividir por el número total de elementos. No obstante, esa no es realmente la razón por la que entré en todo ese detalle. Mi objetivo era tratar de asegurar que todos los que lean este libro tengan claro la notación que usaremos a lo largo del libro:\(\bar{X}\) para la media, para la idea de suma, X i para la iésima observación y N para el número total de observaciones. Vamos a estar reutilizando estos símbolos un poco, así que es importante que los entiendas lo suficientemente bien como para poder “leer” las ecuaciones, y poder ver que es solo decir “sumar muchas cosas y luego dividirlas por otra cosa”.
Cálculo de la media en R
Bien, esas son las matemáticas, ¿cómo conseguimos que la caja mágica de cómputos haga el trabajo por nosotros? Si realmente quisieras, podrías hacer este cálculo directamente en R. Para los primeros 5 puntajes AFL, hazlo con tan solo escribirlo como si R fuera una calculadora...
(56 + 31 + 56 + 8 + 32) / 5## [1] 36.6... en cuyo caso R da salida a la respuesta 36.6, igual que si se tratara de una calculadora. Sin embargo, esa no es la única forma de hacer los cálculos, y cuando el número de observaciones comienza a aumentar, es fácilmente la más tediosa. Además, en casi todos los escenarios del mundo real, ya tienes los números reales almacenados en una variable de algún tipo, al igual que tenemos con la variable afl.margins. En esas circunstancias, lo que quieres es una función que simplemente sume todos los valores almacenados en un vector numérico. Eso es lo que hace la función sum (). Si queremos sumar los 176 márgenes ganadores en el conjunto de datos, podemos hacerlo usando el siguiente comando: 66
sum( afl.margins )## [1] 6213Si solo queremos la suma de las primeras cinco observaciones, entonces podemos usar corchetes para extraer solo los primeros cinco elementos del vector. Entonces el comando sería ahora:
sum( afl.margins[1:5] )## [1] 183Para calcular la media, ahora le decimos a R que divida la salida de esta suma entre cinco, por lo que el comando que necesitamos escribir ahora se convierte en el siguiente:
sum( afl.margins[1:5] ) / 5## [1] 36.6Aunque es bastante fácil calcular la media usando la función sum (), podemos hacerlo de una manera aún más fácil, ya que R también nos proporciona la función mean (). Para calcular la media de los 176 juegos, usaríamos el siguiente comando:
mean( x = afl.margins )
## [1] 35.30114Sin embargo, dado que x es el primer argumento de la función, podría haber omitido el nombre del argumento. En cualquier caso, solo para mostrarte que no está pasando nada gracioso, esto es lo que haríamos para calcular la media de las primeras cinco observaciones:
mean( afl.margins[1:5] )
## [1] 36.6Como puede ver, esto da exactamente las mismas respuestas que los cálculos anteriores.
mediana
La segunda medida de tendencia central que la gente usa mucho es la mediana, y es aún más fácil de describir que la media. La mediana de un conjunto de observaciones es solo el valor medio. Como antes imaginemos solo nos interesaban los primeros 5 márgenes ganadores de AFL: 56, 31, 56, 8 y 32. Para averiguar la mediana, ordenamos estos números en orden ascendente:
8,31, 32 ,56,56
De la inspección, es obvio que el valor medio de estas 5 observaciones es 32, ya que ese es el medio en la lista ordenada (lo he puesto en negrita para hacerlo aún más obvio). Cosas fáciles. Pero, ¿qué debemos hacer si nos interesaban los primeros 6 juegos en lugar de los primeros 5? Dado que el sexto juego de la temporada tuvo un margen ganador de 14 puntos, nuestra lista ordenada es ahora
8,14, 31 ,32,56,56
y hay dos números medios, 31 y 32. La mediana se define como el promedio de esos dos números, que por supuesto es de 31.5. Como antes, es muy tedioso hacer esto a mano cuando tienes muchos números. Para ilustrar esto, esto es lo que sucede cuando usas R para ordenar los 176 márgenes ganadores. Primero, usaré la función sort () (discutida en el Capítulo 7) para mostrar los márgenes ganadores en orden numérico creciente:
sort( x = afl.margins )
## [1] 0 0 1 1 1 1 2 2 3 3 3 3 3 3 3 3 4
## [18] 4 5 6 7 7 8 8 8 8 8 9 9 9 9 9 9 10
## [35] 10 10 10 10 11 11 11 12 12 12 13 14 14 15 16 16 16
## [52] 16 18 19 19 19 19 19 20 20 20 21 21 22 22 22 23 23
## [69] 23 24 24 25 25 26 26 26 26 27 27 28 28 29 29 29 29
## [86] 29 29 30 31 32 32 33 35 35 35 35 36 36 36 36 36 36
## [103] 37 38 38 38 38 38 39 39 40 41 42 43 43 44 44 44 44
## [120] 44 47 47 47 48 48 48 49 49 50 50 50 50 52 52 53 53
## [137] 54 54 55 55 55 56 56 56 57 60 61 61 63 64 65 65 66
## [154] 67 68 70 71 71 72 73 75 75 76 81 82 82 83 84 89 94
## [171] 95 98 101 104 108 116Los valores medios son 30 y 31, por lo que el margen medio ganador para 2010 fue de 30.5 puntos. En la vida real, por supuesto, nadie calcula realmente la mediana ordenando los datos y luego buscando el valor medio. En la vida real, usamos el comando median:
median( x = afl.margins )
## [1] 30.5que da como resultado el valor medio de 30.5.
¿Media o mediana? ¿Cuál es la diferencia?
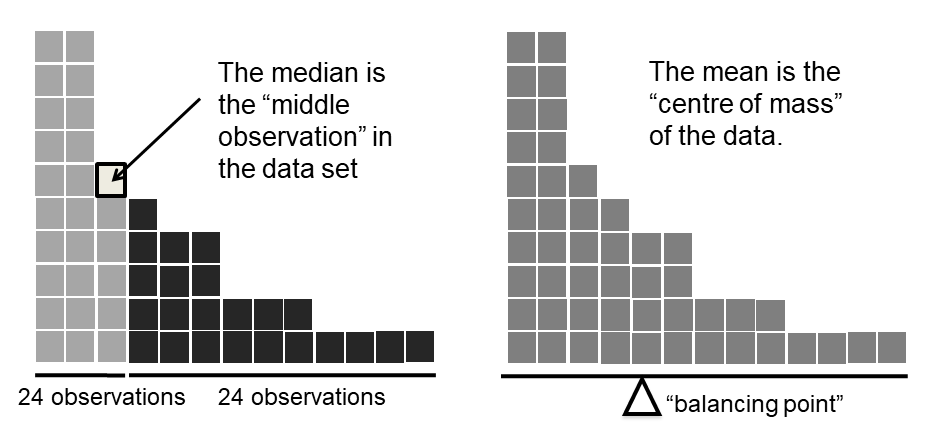
Saber calcular medios y medianas es sólo una parte de la historia. También hay que entender lo que cada uno está diciendo sobre los datos, y lo que eso implica para cuando debes usar cada uno. Esto se ilustra en la Figura 5.2 la media es algo así como el “centro de gravedad” del conjunto de datos, mientras que la mediana es el “valor medio” en los datos. Lo que esto implica, en cuanto a cuál debes usar, depende un poco del tipo de datos que tengas y de lo que intentes lograr. Como guía aproximada:
- Si tus datos son de escala nominal, probablemente no deberías usar ni la media ni la mediana. Tanto la media como la mediana se basan en la idea de que los números asignados a los valores son significativos. Si el esquema de numeración es arbitrario, entonces probablemente sea mejor usar el modo (Sección 5.1.7) en su lugar.
- Si tus datos son escala ordinal, es más probable que quieras usar la mediana que la media. La mediana solo hace uso de la información del pedido en tus datos (es decir, qué números son más grandes), pero no depende de los números precisos involucrados. Esa es exactamente la situación que aplica cuando tus datos son escala ordinal. La media, en cambio, hace uso de los valores numéricos precisos asignados a las observaciones, por lo que no es realmente apropiado para los datos ordinales.
- Para los datos de escala de intervalo y relación, cualquiera de ellos es generalmente aceptable. Cuál eliges depende un poco de lo que intentes lograr. La media tiene la ventaja de que utiliza toda la información de los datos (lo cual es útil cuando no se tienen muchos datos), pero es muy sensible a valores extremos, como veremos en la Sección 5.1.6.
Ampliemos un poco esa última parte. Una consecuencia es que existen diferencias sistemáticas entre la media y la mediana cuando el histograma es asimétrico (sesgado; ver Sección 5.3). Esto se ilustra en la Figura 5.2 notar que la mediana (lado derecho) se ubica más cerca del “cuerpo” del histograma, mientras que la media (lado izquierdo) se arrastra hacia la “cola” (donde están los valores extremos). Para dar un ejemplo concreto, supongamos que Bob (ingresos $50,000), Kate (ingresos $60.000) y Jane (ingresos $65,000) están sentados en una mesa: el ingreso promedio en la mesa es de $58,333 y el ingreso medio es de $60.000. Entonces Bill se sienta con ellos (ingresos $100,000,000). El ingreso promedio ahora ha saltado a 25 mil 043,750 dólares pero la mediana sube sólo a $62,500. Si te interesa ver el ingreso general en la mesa, la media podría ser la respuesta correcta; pero si te interesa lo que cuenta como un ingreso típico en la mesa, la mediana sería una mejor opción aquí.
ejemplo de la vida real
Para tratar de tener una idea de por qué hay que prestar atención a las diferencias entre la media y la mediana, consideremos un ejemplo de la vida real. Ya que tiendo a burlarme de los periodistas por sus escasos conocimientos científicos y estadísticos, debería dar crédito donde se debe el crédito. Esto es de un excelente artículo en la página de noticias ABC 67 24 septiembre, 2010:
Los altos ejecutivos del Commonwealth Bank han viajado por el mundo en las últimas semanas con una presentación en la que se muestra cómo los precios de las casas australianas, y las relaciones clave entre precio e ingresos, se comparan favorablemente con países similares. “La asequibilidad de la vivienda en realidad ha estado yendo de lado durante los últimos cinco a seis años”, dijo Craig James, el economista jefe del brazo comercial del banco, CommSec.
Esto probablemente sea una gran sorpresa para cualquiera que tenga una hipoteca, o que quiera una hipoteca, o pague el alquiler, o no sea completamente ajeno a lo que ha estado sucediendo en el mercado inmobiliario australiano en los últimos años. Volver al artículo:
CBA ha librado su guerra contra lo que cree que son albergar a los doomsayers con gráficas, números y comparaciones internacionales. En su presentación, el banco rechaza los argumentos de que la vivienda de Australia es relativamente cara en comparación con los ingresos. Dice que la relación entre el precio de la vivienda y el ingreso familiar de Australia de 5.6 en las principales ciudades, y 4.3 a nivel nacional, es comparable a la de muchas otras naciones desarrolladas. Dice que San Francisco y Nueva York tienen proporciones de 7, la de Auckland es de 6.7 y Vancouver entra en 9.3.
¡Más excelentes noticias! Salvo que el artículo continúa haciendo la observación de que...
Muchos analistas dicen que eso ha llevado al banco a utilizar cifras y comparaciones engañosas. Si vas a la página cuatro de la presentación de CBA y lees la información de origen en la parte inferior de la gráfica y tabla, notarás que hay una fuente adicional en la comparación internacional: Demografía. Sin embargo, si el Commonwealth Bank también hubiera utilizado el análisis de Demographia de la relación precio de la vivienda a ingresos de Australia, habría llegado a una cifra más cercana a 9 en lugar de 5.6 o 4.3
Eso es, um, una discrepancia bastante seria. Un grupo de personas dice 9, otro dice 4-5. ¿Deberíamos dividir la diferencia y decir que la verdad se encuentra en algún punto intermedio? Absolutamente no: esta es una situación en la que hay una respuesta correcta y una respuesta incorrecta. La demografía es correcta, y el Banco del Commonwealth es incorrecto. Como señala el artículo
[Un] problema obvio con las cifras del precio interno a los ingresos del Commonwealth Bank es que comparan los ingresos promedio con los precios medios de la vivienda (a diferencia de las cifras de Demographia que comparan los ingresos medios con los precios medios). La mediana es el punto medio, efectivamente recortando los máximos y mínimos, y eso significa que el promedio es generalmente más alto cuando se trata de ingresos y precios de activos, porque incluye las ganancias de las personas más ricas de Australia. Para decirlo de otra manera: las cifras del Commonwealth Bank cuentan el paquete de pago multimillonario de Ralph Norris en el lado de los ingresos, pero no su (sin duda) casa muy cara en las cifras de precio de la propiedad, subestimando así la relación precio-ingreso de la casa para los australianos de ingresos medios.
Yo no lo podría haber puesto mejor. La forma en que Demographia calculó la relación es lo correcto. La forma en que lo hizo el Banco es incorrecta. En cuanto a por qué una organización extremadamente sofisticada cuantitativamente como un banco importante cometió un error tan elemental, bueno... No puedo decirlo con certeza, ya que no tengo una visión especial de su pensamiento, pero el artículo en sí sí menciona los siguientes hechos, que pueden o no ser relevantes:
[Como] el prestamista de viviendas más grande de Australia, el Commonwealth Bank tiene uno de los mayores intereses creados en el aumento de los precios de la vivienda. Efectivamente posee una franja masiva de viviendas australianas como garantía para sus préstamos hipotecarios, así como muchos préstamos para pequeñas empresas.
Mi, mi.
Media recortada
Una de las reglas fundamentales de la estadística aplicada es que los datos son desordenados. La vida real nunca es simple, por lo que los conjuntos de datos que obtienes nunca son tan sencillos como dice la teoría estadística. 68 Esto puede tener consecuencias incómodas. Para ilustrar, considere este conjunto de datos de aspecto bastante extraño:
−100,2,3,4,5,6,7,8,9,10
Si tuvieras que observar esto en un conjunto de datos de la vida real, probablemente sospecharías que algo gracioso estaba pasando con el valor −100. Probablemente sea un valor atípico, un valor que realmente no pertenece a los demás. Podría considerar eliminarlo del conjunto de datos por completo, y en este caso en particular probablemente estaría de acuerdo con ese curso de acción. En la vida real, sin embargo, no siempre se obtienen esos ejemplos de corte y secado. Por ejemplo, podrías obtener esto en su lugar:
−15,2,3,4,5,6,7,8,9,12
El −15 parece un poco sospechoso, pero no tan cerca como lo hizo el −100. En este caso, es un poco más complicado. Podría ser una observación legítima, tal vez no.
Ante una situación en la que algunas de las observaciones de mayor valor extremo podrían no ser del todo confiables, la media no es necesariamente una buena medida de tendencia central. Es altamente sensible a uno o dos valores extremos, y por lo tanto no se considera una medida robusta. Un remedio que hemos visto es usar la mediana. Una solución más general es usar una “media recortada”. Para calcular una media recortada, lo que haces es “descartar” los ejemplos más extremos en ambos extremos (es decir, el más grande y el más pequeño), y luego tomar la media de todo lo demás. El objetivo es preservar las mejores características de la media y la mediana: al igual que una mediana, no estás muy influenciado por valores atípicos extremos, pero como la media, “usas” más de una de las observaciones. Generalmente, describimos una media recortada en términos del porcentaje de observación en cada lado que se descartan. Entonces, por ejemplo, una media recortada del 10% descarta el mayor 10% de las observaciones y el 10% más pequeño de las observaciones, y luego toma la media del 80% restante de las observaciones. No es sorprendente que la media recortada del 0% sea solo la media regular, y la media recortada del 50% es la mediana. En ese sentido, las medias recortadas proporcionan toda una familia de medidas de tendencia central que abarcan el rango de la media a la mediana.
Para nuestro ejemplo de juguete anterior, tenemos 10 observaciones, y así se calcula una media recortada del 10% ignorando el valor más grande (es decir, 12) y el valor más pequeño (es decir, -15) y tomando la media de los valores restantes. Primero, ingresemos los datos
dataset <- c( -15,2,3,4,5,6,7,8,9,12 )A continuación, calculemos medias y medianas:
mean( x = dataset )
## [1] 4.1median( x = dataset )
## [1] 5.5Esa es una diferencia bastante sustancial, pero estoy tentado a pensar que la media está siendo influenciada un poco demasiado por los valores extremos en cada extremo del conjunto de datos, especialmente el −15. Así que intentemos recortar un poco la media. Si tomo una media recortada del 10%, bajaremos los valores extremos en cada lado, y tomaremos la media del resto:
mean( x = dataset, trim = .1)
## [1] 5.5que en este caso da exactamente la misma respuesta que la mediana. Tenga en cuenta que, para obtener un 10% recortado significa que escribe trim = .1, no trim = 10. En cualquier caso, terminemos calculando la media recortada del 5% para los datos afl.margins,
mean( x = afl.margins, trim = .05)
## [1] 33.75Modo
El modo de una muestra es muy sencillo: es el valor que ocurre con mayor frecuencia. Para ilustrar el modo usando los datos de AFL, examinemos un aspecto diferente al conjunto de datos. ¿Quién ha jugado en la mayor cantidad de finales? La variable afl.finalistas es un factor que contiene el nombre de cada equipo que jugó en cualquier final de la AFL de 1987-2010, así que vamos a echarle un vistazo. Para ello usaremos el comando head (). head () es útil cuando estás trabajando con un data.frame con muchas filas ya que puedes usarlo para decirte cuántas filas devolver. Ha habido muchas finales en este periodo así que imprimir afl.finalistas usando print (afl.finalistas) solo nos llenará la pantalla. El siguiente comando le dice a R que solo queremos las primeras 25 filas del data.frame.
head(afl.finalists, 25)## [1] Hawthorn Melbourne Carlton Melbourne Hawthorn
## [6] Carlton Melbourne Carlton Hawthorn Melbourne
## [11] Melbourne Hawthorn Melbourne Essendon Hawthorn
## [16] Geelong Geelong Hawthorn Collingwood Melbourne
## [21] Collingwood West Coast Collingwood Essendon Collingwood
## 17 Levels: Adelaide Brisbane Carlton Collingwood Essendon ... Western BulldogsEn realidad hay 400 entradas (¿no te alegras de que no las imprimimos todas?). Podríamos leer los 400, y contar el número de ocasiones en que cada nombre de equipo aparece en nuestra lista de finalistas, produciendo así una tabla de frecuencias. Sin embargo, eso sería sin sentido y aburrido: exactamente el tipo de tarea en la que las computadoras son geniales. Entonces usemos la función table () (discutida con más detalle en la Sección 7.1) para hacer esta tarea por nosotros:
table( afl.finalists )## afl.finalists
## Adelaide Brisbane Carlton Collingwood
## 26 25 26 28
## Essendon Fitzroy Fremantle Geelong
## 32 0 6 39
## Hawthorn Melbourne North Melbourne Port Adelaide
## 27 28 28 17
## Richmond St Kilda Sydney West Coast
## 6 24 26 38
## Western Bulldogs
## 24Ahora que tenemos nuestra tabla de frecuencias, solo podemos mirarla y ver que, a lo largo de los 24 años para los que tenemos datos, Geelong ha jugado en más finales que cualquier otro equipo. Así, el modo de los datos finalistas es “Geelong”. Los paquetes core en R no tienen una función para calcular el modo 69. Sin embargo, he incluido una función en el paquete lsr que hace esto. La función se llama modeOf (), y así es como la usas:
modeOf( x = afl.finalists )## [1] "Geelong"También hay una función llamada maxFreq () que te dice cuál es la frecuencia modal. Si aplicamos esta función a nuestros datos finalistas, obtenemos lo siguiente:
maxFreq( x = afl.finalists )## [1] 39Tomados en conjunto, observamos que Geelong (39 finales) jugó en más finales que cualquier otro equipo durante el periodo 1987-2010.
Un último punto a hacer con respecto a la modalidad. Si bien en general es cierto que el modo se calcula con mayor frecuencia cuando se tienen datos de escala nominal (porque las medias y las medianas son inútiles para ese tipo de variables), hay algunas situaciones en las que realmente se quiere conocer el modo de una variable de escala ordinal, de intervalo o de relación. Por ejemplo, volvamos a pensar en nuestra variable afl.margins. Esta variable es claramente escala de ratio (si no te queda claro, puede ayudar releer la Sección 2.2), y así en la mayoría de las situaciones la media o la mediana es la medida de tendencia central que deseas. Pero considera este escenario... un amigo tuyo está ofreciendo una apuesta. Escogen un partido de fútbol al azar, y (sin saber quién está jugando) hay que adivinar el margen exacto. Si adivina correctamente, gana $50. Si no lo haces, pierdes $1. No hay premios de consolación por “casi” obtener la respuesta correcta. Tienes que adivinar exactamente el margen derecho 70 Para esta apuesta, la media y la mediana son completamente inútiles para ti. Es el modo en el que debes apostar. Entonces, calculamos este valor modal
modeOf( x = afl.margins )## [1] 3
maxFreq( x = afl.margins )## [1] 8Por lo que los datos de 2010 sugieren que debes apostar por un margen de 3 puntos, y como esto se observó en 8 del juego 176 (4.5% de los juegos) las probabilidades están firmemente a tu favor.


