2.2: Intervalos de confianza

En el capítulo anterior aprendimos que las poblaciones se caracterizan por medidas descriptivas llamadas parámetros. Las inferencias sobre los parámetros se basan en estadísticas de muestra. Ahora queremos estimar los parámetros poblacionales y evaluar la confiabilidad de nuestras estimaciones con base en nuestro conocimiento de las distribuciones de muestreo de estas estadísticas.

Estimaciones de puntos

Comenzamos con una estimación puntual. Se trata de un valor único calculado a partir de los datos de la muestra que se utiliza para estimar el parámetro poblacional de interés.

• La media muestral (\(\bar {x}\)) es una estimación puntual de la media poblacional (\(\mu\)).
• La proporción muestral (\(\hat {p}\)) es la estimación puntual de la proporción poblacional (p).

Utilizamos estimaciones puntuales para construir intervalos de confianza para parámetros desconocidos.

• Un intervalo de confianza es un intervalo de valores en lugar de una estimación de un solo punto.
• El nivel de confianza corresponde a la proporción esperada de intervalos que contendrán el parámetro si se construyen muchos intervalos de confianza del mismo tamaño de muestra de la misma población.
• Nuestra incertidumbre se refiere a si nuestro intervalo de confianza particular es uno de los que realmente contiene el verdadero valor del parámetro.

Ejemplo\(\PageIndex{1}\): bear weight

Estamos 95% seguros de que nuestro intervalo contiene el peso medio del oso de la población.

Si creamos 100 intervalos de confianza del mismo tamaño a partir de una misma población, esperaríamos que 95 de ellos contengan el parámetro verdadero (el peso medio poblacional). También esperamos que cinco de los intervalos no contendrían el parámetro.

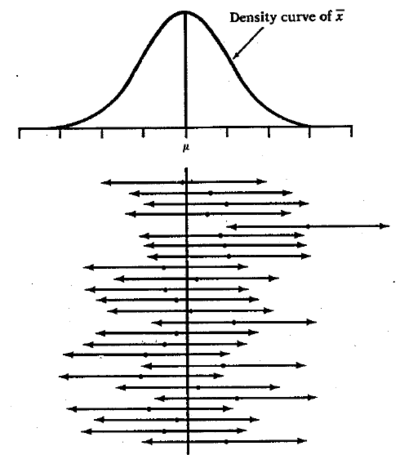
Figura\(\PageIndex{1}\): Intervalos de confianza de veinticinco muestras diferentes.

En este ejemplo, veinticinco muestras de una misma población dieron estos intervalos de confianza del 95%. A largo plazo, 95% de todas las muestras dan un intervalo que contiene µ, la media poblacional verdadera (pero desconocida).

El nivel de confianza se expresa como un porcentaje.

• El cumplido al nivel de confianza es α (alfa), el nivel de significancia.
• El nivel de confianza se describe como\((1- \alpha) \times 100%\).

¿Qué significa esto realmente?

• Se utiliza una estimación puntual (p. ej., media muestral) para estimar la media poblacional.
• Adjuntamos un nivel de confianza a este intervalo para describir cuán seguros estamos de que este intervalo realmente contiene el parámetro de población desconocido.
• Queremos estimar el parámetro poblacional, como la media (μ) o la proporción (p).

\[\bar {x}-E < \mu < \bar {x}+E\]

o

\[\hat {p}-E < p <\hat {p}+E\]

donde\(E\) está el margen de error.

La confianza se basa en el área bajo una curva normal. Por lo que debe cumplirse el supuesto de normalidad (Capítulo 1).

Intervalos de Confianza sobre la Media (μ) cuando se conoce la Desviación Estándar de la Población (σ)

Un intervalo de confianza toma la forma de: \(\pm\)margen de error estimado de punto.

La estimación del punto

• La estimación puntual proviene de los datos de la muestra.
• Para estimar la media poblacional (\(μ\)), utilice la media muestral (\(\bar{x}\)) como estimación puntual.

El margen de error

• Depende del nivel de confianza, el tamaño de la muestra y la desviación estándar de la población.
• Se calcula como\(E=Z_{\frac {\alpha}{2}}\times \frac {\sigma}{\sqrt {n}}\) donde\(Z_{\frac {\alpha}{2}}\) está el valor crítico de la tabla normal estándar asociada con α (el nivel de significancia).

El valor crítico\(Z_{\frac {\alpha}{2}}\)

• Este es un puntaje Z que borra el nivel de confianza.
• Los intervalos de confianza son SIEMPRE de dos caras y los puntajes Z son los límites del área asociada con el nivel de confianza.

Figura\(\PageIndex{1}\): El área media del 95% bajo una curva normal estándar.

• El nivel de significancia (α) se divide en mitades porque estamos mirando el 95% medio del área bajo la curva.
• Acude a tu tabla normal estándar y encuentra el área de 0.025 en el cuerpo de valores.
• ¿Cuál es el puntaje Z para esa área?
• Las puntuaciones Z de ± 1.96 son las puntuaciones Z críticas para un intervalo de confianza del 95%.

Tabla\(\PageIndex{1}\): Valores críticos comunes (puntuaciones Z).

Pasos

Construcción de un intervalo de confianza sobre\(μ\) cuándo\(σ\) se conoce:

1. \(Z_{\frac {\alpha}{2}}\)(valor crítico)
2. \(E=Z_{\frac {\alpha}{2}}\times \frac {\sigma}{\sqrt {n}}\)(margen de error)
3. \(\bar {x} \pm E\)(estimación puntual ± margen de error)

Ejemplo\(\PageIndex{3}\): Construct a confidence interval about the population mean

Los investigadores han estado estudiando la carga p en Jones Lake durante muchos años. Se sabe que la claridad media del agua (usando un disco Secchi) se distribuye normalmente con una desviación estándar poblacional de σ = 15.4 pulg. Se tomó una muestra aleatoria de 22 mediciones en diversos puntos del lago con una media muestral de x̄ = 57.8 pulg. Los investigadores quieren que construyas un intervalo de confianza del 95% para μ, la claridad media del agua.

Un disco secchi para medir turbiamente de agua. (CC SA; publiclab.org)

Solución

1)\(Z_{\frac {\alpha}{2}}\) = 1.96

2)\(E=Z_{\frac {\alpha}{2}}\times \frac {\sigma}{\sqrt {n}}\) =\(1.96 \times \frac {15.4}{\sqrt {22}}\) = 6.435

3)\(\bar {x} \pm E\) = 57.8 ± 6.435

El intervalo de confianza del 95% para la claridad media del agua es (51.36, 64.24).

Podemos estar 95% seguros de que este intervalo contiene la claridad media del agua de la población para Jones Lake.

Ahora construya un intervalo de confianza del 99% para μ, la claridad media del agua, e interprete.

1)\(Z_{\frac {\alpha}{2}}\) = 2.575

2)\(E=Z_{\frac {\alpha}{2}}\times \frac {\sigma}{\sqrt {n}}\) =\(2.575 \times \frac {15.4}{\sqrt {22}}\) = 8.454

3)\(\bar {x} \pm E\) = 57.8± 8.454

El intervalo de confianza del 99% para la claridad media del agua es (49.35, 66.25).

Podemos estar 99% seguros de que este intervalo contiene la claridad media del agua de la población para Jones Lake.

A medida que el nivel de confianza aumentó de 95% a 99%, el ancho del intervalo aumentó. A medida que aumentaba la probabilidad (área bajo la curva normal), el valor crítico aumentó dando como resultado un intervalo más amplio.

Soluciones de Software

Minitab

Puede usar Minitab para construir este intervalo de confianza del 95% (Excel no construye intervalos de confianza sobre la media cuando se conoce la desviación estándar de la población). Seleccionar Estadística básica>1-Muestra Z. Ingresa la desviación estándar de la población conocida y selecciona el nivel de confianza requerido.

Figura 3. Capturas de pantalla de Minitab para construir un intervalo de confianza.

Una muestra Z: profundidad

La desviación estándar asumida = 15.4

Variable	N	Media	StDev	SE Media	95% CI
profundidad	22	57.80	11.60	3.28	(51.36, 64.24)

Intervalos de confianza sobre la Media (μ) cuando la Desviación Estándar de la Población (σ) es Desconocida

Por lo general, en la vida real muchas veces no conocemos la desviación estándar de la población (σ). Podemos utilizar la desviación estándar de la muestra en lugar de σ. Sin embargo, debido a este cambio, no podemos usar la distribución normal estándar para encontrar los valores críticos necesarios para construir un intervalo de confianza.

La distribución t de Student se creó para situaciones en las que σ era desconocida. Gosset trabajó como ingeniero de control de calidad para Guinness Brewery en Dublín. Encontró errores en sus pruebas y sabía que se debía al uso de s en lugar de σ. Creó esta distribución para hacer frente al problema de una desviación estándar poblacional desconocida y pequeños tamaños muestrales. A continuación se muestra una porción de la tabla t.

Tabla\(\PageIndex{2}\): Porción de la mesa t del estudiante.

Ejemplo\(\PageIndex{4}\)

Encontrar el valor crítico\(t_{\frac {\alpha}{2}}\) para un intervalo de confianza del 95% con un tamaño muestral de n=13.

Solución

• Grados de libertad (abajo de la columna de la izquierda) es igual a n-1 = 12
• α = 0.05 y α/2 = 0.025
• Bajar la columna 0.025 a 12 df
• \(t_{\frac {\alpha}{2}}\)= 2.179

Los valores críticos de la distribución t de los estudiantes se acercan a los valores críticos de la distribución normal estándar a medida que aumenta el tamaño de la muestra (n).

Cuadro 3. Valores críticos de la tabla t del estudiante.

Usando la curva normal estándar, el valor crítico para un intervalo de confianza del 95% es de 1.96. Se puede ver cómo los diferentes tamaños de muestras cambiarán el valor crítico y por lo tanto el intervalo de confianza, especialmente cuando el tamaño de la muestra es pequeño.

Construcción de un Intervalo de Confianza

Cuando σ es Desconocido

1. \(t_{\frac {\alpha}{2}}\)valor crítico con n-1 df
2. \(E = t_{\frac {\alpha}{2}} \times \frac{s}{\sqrt {n}}\)
3. \(\bar {x} \pm E\)

Ejemplo\(\PageIndex{5}\):

Investigadores que estudian los efectos de la lluvia ácida en las montañas Adirondack recolectaron muestras de agua de 22 lagos. Midieron el pH (acidez) del agua y quieren construir un intervalo de confianza del 99% sobre el pH medio del lago para esta región. La media muestral es 6.4438 con una desviación estándar muestral de 0.7120. No saben nada sobre la distribución del pH de esta población, y la muestra es pequeña (n<30), por lo que miran una gráfica de probabilidad normal.

Figura 4. Parcela de probabilidad normal.

Solución

Los datos se distribuyen normalmente. Ahora construya el intervalo de confianza del 99% sobre el pH medio.

1)\(t_{\frac {\alpha}{2}}\) = 2.831

2)\(E = t_{\frac {\alpha}{2}} \times \frac{s}{\sqrt {n}}\) =\(2.831 \times \frac {0.7120}{\sqrt {22}}\) = 0.4297

3)\(\bar {x} \pm E\) = 6.443 ± 0.4297

El intervalo de confianza del 99% sobre el pH medio es (6.013, 6.863).

Estamos 99% seguros de que este intervalo contiene el pH medio del lago para esta población lacustre.

Ahora construya un intervalo de confianza del 90% sobre el pH medio para estos lagos.

1)\(t_{\frac {\alpha}{2}}\) = 1.721

2)\(E = t_{\frac {\alpha}{2}} \times \frac{s}{\sqrt {n}}\) =\(1.71221 \times \frac {0.7120}{\sqrt {22}}\) 0.2612

3)\(\bar {x} \pm E\) = 6.443 ± 0.2612

El intervalo de confianza del 90% sobre el pH medio es (6.182, 6.704).

Estamos 90% seguros de que este intervalo contiene el pH medio del lago para esta población lacustre.

Observe cómo el ancho del intervalo disminuyó a medida que el nivel de confianza disminuyó de 99 a 90%.

Construir un intervalo de confianza de 90% sobre el pH medio del lago usando Excel y Minitab.

Soluciones de Software

Minitab

Para Minitab, ingrese los datos en la hoja de cálculo y seleccione Estadísticas básicas y prueba t de 1 muestra.

T de una muestra: pH

Variable	N	Media	StDev	SE Media	90% CI
pH	22	6.443	0.712	0.152	(6.182, 6.704)

Ejemplo adicional:

Excel

Para Excel, ingrese los datos en la hoja de cálculo y seleccione estadísticas descriptivas. Consulta Estadísticas de Resumen y selecciona el nivel y la confianza.

Media	6.442909
Error estándar	0.151801
Mediana	6.4925
Modo	#N /A
Desviación estándar	0.712008
Varianza de la muestra	0.506956
Curtosis	-0.5007
Asimetría	-0.60591
Rango	2.338
Mínimo	5.113
Máximo	7.451
Suma	141.744
Contar	22
Nivel de Confianza (90.0%)	0.26121

Excel te da la media muestral en la primera línea (6.442909) y el margen de error en la última línea (0.26121). Debe completar el cálculo usted mismo para obtener el intervalo (6.442909±0.26121).

Intervalos de confianza sobre la proporción poblacional (p)

Frecuentemente, nos interesa estimar la proporción poblacional (p), en lugar de la media poblacional (µ). Por ejemplo, es posible que deba estimar la proporción de árboles infectados con la enfermedad de la corteza de haya, o la proporción de personas que apoyan productos “verdes”. El parámetro p se puede estimar de la misma manera que se estimó µ, la media poblacional.

La proporción de la muestra

• La proporción muestral es la mejor estimación puntual para la verdadera proporción poblacional.
• Proporción muestral\(\hat {p} = \frac {x}{n}\) donde x es el número de elementos en la muestra con la característica que le interesa, y n es el tamaño de la muestra.

La Asunción de la Normalidad al Estimar Proporciones

• El supuesto de una población normalmente distribuida sigue siendo importante, a pesar de que el parámetro ha cambiado.
• La normalidad se puede verificar si: $$ n\ times\ hat {p}\ times (1-\ hat {p})\ ge 10$$

Construir un Intervalo de Confianza sobre la Proporción de Población

La construcción de un intervalo de confianza sobre la proporción sigue los mismos tres pasos que hemos utilizado en los ejemplos anteriores.

1. \(Z_{\frac {\alpha}{2}}\)(valor crítico de la tabla normal estándar)
2. \(E = Z_{\frac {\alpha}{2}} \times \sqrt {\frac{\hat {p}(1-\hat {p})}{n}}\)(margen de error)
3. \(\hat {p} \pm E\)(estimación puntual ± margen de error)

Ejemplo\(\PageIndex{6}\):

Un botánico ha producido una nueva variedad de soja híbrida que es mejor capaz de soportar la sequía. Ella quiere construir un intervalo de confianza del 95% sobre la tasa de germinación (porcentaje de germinación). Ella seleccionó al azar 500 semillas y encontró que 421 han germinado.

Solución

Primero, compute la estimación del punto

\[\hat {p} = \frac {x}{n} =\frac {421}{500}=0.842\]

Comprobar normalidad:

$$n\ times\ hat {p}\ times (1-\ hat {p})\ ge 10 = 500\ times 0.842\ times (1-0.842) =66,5\]

Se puede asumir una distribución normal.

Ahora construye el intervalo de confianza:

1)\(Z_{\frac {\alpha}{2}}\) = 1.96

2)\(E = Z_{\frac {\alpha}{2}} \times \sqrt {\frac{\hat {p}(1-\hat {p})}{n}}\) =\(1.96 \times \sqrt {\frac {0.842(1-0.842)}{500}}\) = 0.032

3)\(\hat {p} \pm E =0.842 \pm 0.0032\)

El intervalo de confianza del 95% para la tasa de germinación es (81.0%, 87.4%).

Podemos estar 95% seguros de que este intervalo contiene la verdadera tasa de germinación para esta población.

Soluciones de Software

Minitab

Puede usar Minitab para calcular el intervalo de confianza. Seleccione estado>Estados básicos>1-proporción. Seleccione los datos resumidos e ingrese el número de eventos (421) y el número de ensayos (500). Haga clic en Opciones y seleccione el nivel de confianza correcto. Verificar “prueba e intervalo basado en la distribución normal” si se ha verificado el supuesto de normalidad.

Prueba e IC para una proporción

Muestra	X	N	Muestra p	95% CI
1	421	500	0.842000	(0.810030, 0.873970)

Usando la aproximación normal.

Excel

Excel no computa intervalos de confianza para estimar la proporción poblacional.

Resumen del intervalo de confianza

¿Qué método utilizo?

La primera pregunta que debes hacerte es: ¿Qué parámetro estás tratando de estimar? Si es la media (µ), entonces pregúntese: ¿Se conoce la desviación estándar de la población (σ)? En caso afirmativo, siga los siguientes 3 pasos:

Intervalo de confianza sobre la media poblacional (µ) cuando σ es conocida

1. \(Z_{\frac {\alpha}{2}}\)valor crítico (de la tabla normal estándar)
2. \(E=Z_{\frac {\alpha}{2}} \times \frac {\sigma}{\sqrt {n}}\)
3. \(\bar {x} \pm E\)

Si no, sigue estos 3 pasos:

Intervalo de confianza sobre la media poblacional (µ) cuando σ es Desconocida

1. \(t_{\frac {\alpha}{2}}\)valor crítico con n-1 df de la distribución t de estudiante
2. \(E=t_{\frac {\alpha}{2}} \times \frac {s}{\sqrt {n}}\)
3. \(\bar {x} \pm E\)

Si quieres construir un intervalo de confianza sobre la proporción de población, sigue estos 3 pasos:

Intervalo de confianza sobre la proporción

1. \(Z_{\frac {\alpha}{2}}\)valor crítico de la tabla normal estándar
2. \(E = Z_{\frac {\alpha}{2}} \times \sqrt {\frac{\hat {p}(1-\hat {p})}{n}}\)
3. \(\hat {p} \pm E\)

Recuerda que se debe verificar el supuesto de normalidad.