10.2: Cuando las cosas van mal con los residuos
- Page ID
- 150069
El análisis residual es el proceso de búsqueda de patrones de firma en los residuales que son indicativos de una falla en los supuestos subyacentes de regresión de OLS. Diferentes tipos de problemas conducen a diferentes patrones en los residuos.
10.2.1 Datos “atípicos”
En ocasiones nuestros datos incluyen casos inusuales que se comportan de manera diferente a la mayoría de nuestras observaciones. Esto puede suceder por varias razones. Lo más típico es que los datos han sido mal codificados, con algún subgrupo de los datos que tienen valores numéricos que conducen a grandes residuos. Casos como este también pueden surgir cuando un subgrupo de los casos difiere de los demás en cómo XX influye YY, y esa diferencia no ha sido capturada en el modelo. Se trata de un problema al que se hace referencia como la omisión de importantes variables independientes. 18 La figura\(\PageIndex{3}\) muestra un ejemplo estilizado, con un cúmulo de residuos que caen a una distancia considerable del resto.
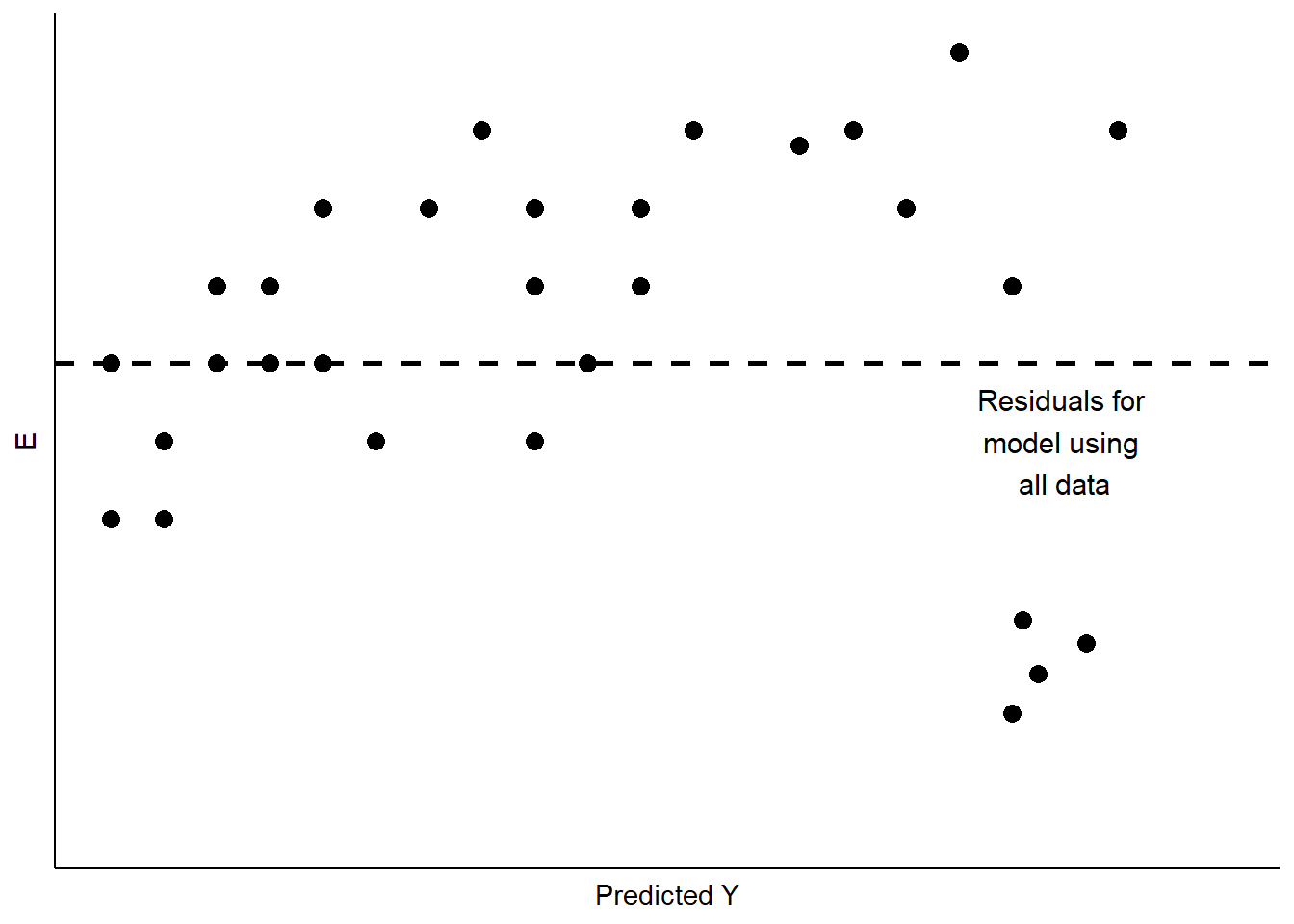
Este es un caso de valores atípicos influyentes. El efecto de tales valores atípicos puede ser significativo, ya que las estimaciones de OLS de AA y BB buscan minimizar el error cuadrado general. En el caso de la Figura\(\PageIndex{3}\), el efecto sería desplazar la estimación de BB para acomodar las observaciones inusuales, como se ilustra en la Figura\(\PageIndex{4}\). Una posible respuesta sería omitir las observaciones inusuales, como se muestra en la Figura\(\PageIndex{4}\). Otro sería considerar, teórica y empíricamente, por qué estas observaciones son inusuales. ¿Están, quizás, mal codificados? ¿O son códigos que representan valores faltantes (por ejemplo, “-99”)?
Si no son códigos erróneos, tal vez estas observaciones atípicas manifiesten un tipo diferente de relación entre XX y YY, que a su vez, podría requerir una teoría y un modelo revisados. Abordaremos algunas opciones de modelado para abordar esta posibilidad cuando exploremos la regresión múltiple, en la Parte III de este libro.
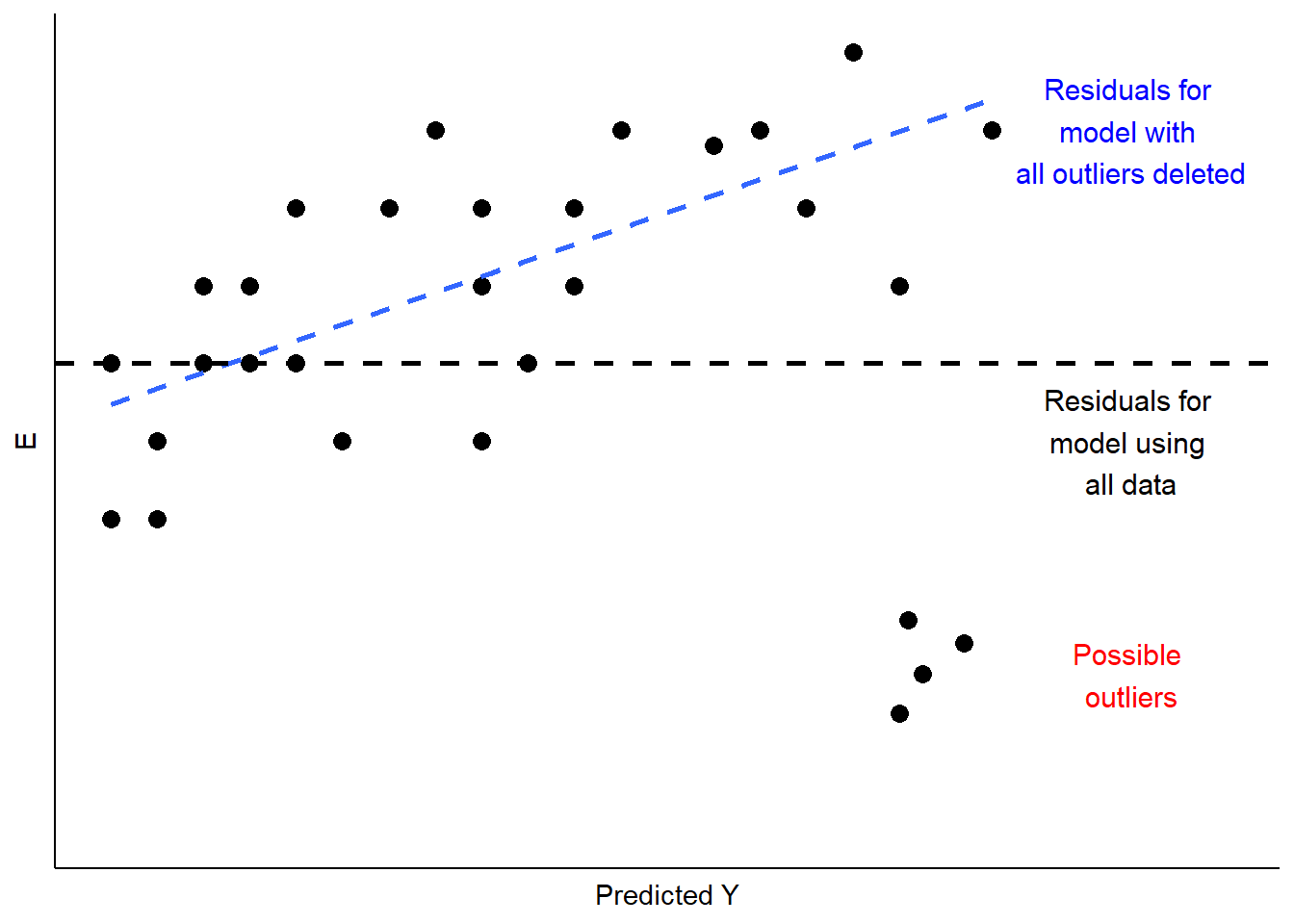
En suma, el análisis de valores atípicos analiza los residuos para patrones en los que algunas observaciones se desvían ampliamente de otras. Si esa desviación es influyente, cambiando las estimaciones de AA y BB como se muestra en la Figura\(\PageIndex{4}\), entonces debe examinar las observaciones para determinar si están mal codificadas. De no ser así, puede evaluar si los casos son teóricamente distintos, de tal manera que la influencia de XX en YY probablemente sea diferente a la de otros casos. Si llegas a la conclusión de que esto es así, necesitarás reespecificar tu modelo para dar cuenta de estas diferencias. Discutiremos algunas opciones para hacerlo más adelante en este capítulo, y nuevamente en nuestra discusión de regresión múltiple.
10.2.2 Varianza no constante
Una segunda cosa a buscar en el diagnóstico visual de residuos es la varianza no constante o heterocedasticidad. En este caso, la variación en los residuos sobre el rango de valores predichos para YY debe ser aproximadamente uniforme. Un problema ocurre cuando esa variación cambia sustancialmente a medida que cambia el valor predicho de YY, como se ilustra en la Figura\(\PageIndex{5}\).
## x5 y5 z5
## 1 1 0.116268529 first
## 2 2 -0.058592447 first
## 3 3 0.178546500 first
## 4 4 -0.133259371 first
## 5 5 -0.044656677 first
## 6 6 0.056960612 first
## 7 7 -0.288971761 first
## 8 8 -0.086901834 first
## 9 9 -0.046170268 first
## 10 10 -0.055554091 first
## 11 11 -0.002013537 first
## 12 12 -0.015038222 first
## 13 13 -0.062812676 first
## 14 14 0.132322085 first
## 15 15 -0.152135057 first
## 16 16 -0.043742787 first
## 17 17 0.097057758 first
## 18 18 0.002822264 first
## 19 19 -0.008578219 first
## 20 20 0.038921440 first
## 21 21 0.023668737 first## x5 y5 z5
## 1 21 -0.7944212 second
## 2 22 3.9722634 second
## 3 23 2.0344877 second
## 4 24 -1.3313647 second
## 5 25 -8.0963483 second
## 6 26 -3.2788775 second
## 7 27 -6.3068507 second
## 8 28 -13.6105004 second
## 9 29 -3.3742972 second
## 10 30 -1.1897133 second
## 11 31 8.7458017 second
## 12 32 8.5587880 second
## 13 33 6.0964799 second
## 14 34 -6.0353801 second
## 15 35 -10.2333314 second
## 16 36 -5.0246837 second
## 17 37 6.8506290 second
## 18 38 0.4832010 second
## 19 39 2.3291504 second
## 20 40 -4.5016566 second
## 21 41 -8.4841231 second## x5 y5 z5
## 1 1 0.116268529 first
## 2 2 -0.058592447 first
## 3 3 0.178546500 first
## 4 4 -0.133259371 first
## 5 5 -0.044656677 first
## 6 6 0.056960612 first
## 7 7 -0.288971761 first
## 8 8 -0.086901834 first
## 9 9 -0.046170268 first
## 10 10 -0.055554091 first
## 11 11 -0.002013537 first
## 12 12 -0.015038222 first
## 13 13 -0.062812676 first
## 14 14 0.132322085 first
## 15 15 -0.152135057 first
## 16 16 -0.043742787 first
## 17 17 0.097057758 first
## 18 18 0.002822264 first
## 19 19 -0.008578219 first
## 20 20 0.038921440 first
## 21 21 0.023668737 first
## 22 21 -0.794421247 second
## 23 22 3.972263354 second
## 24 23 2.034487716 second
## 25 24 -1.331364730 second
## 26 25 -8.096348251 second
## 27 26 -3.278877502 second
## 28 27 -6.306850722 second
## 29 28 -13.610500382 second
## 30 29 -3.374297181 second
## 31 30 -1.189713327 second
## 32 31 8.745801727 second
## 33 32 8.558788016 second
## 34 33 6.096479914 second
## 35 34 -6.035380147 second
## 36 35 -10.233331440 second
## 37 36 -5.024683664 second
## 38 37 6.850629016 second
## 39 38 0.483200951 second
## 40 39 2.329150423 second
## 41 40 -4.501656591 second
## 42 41 -8.484123104 second
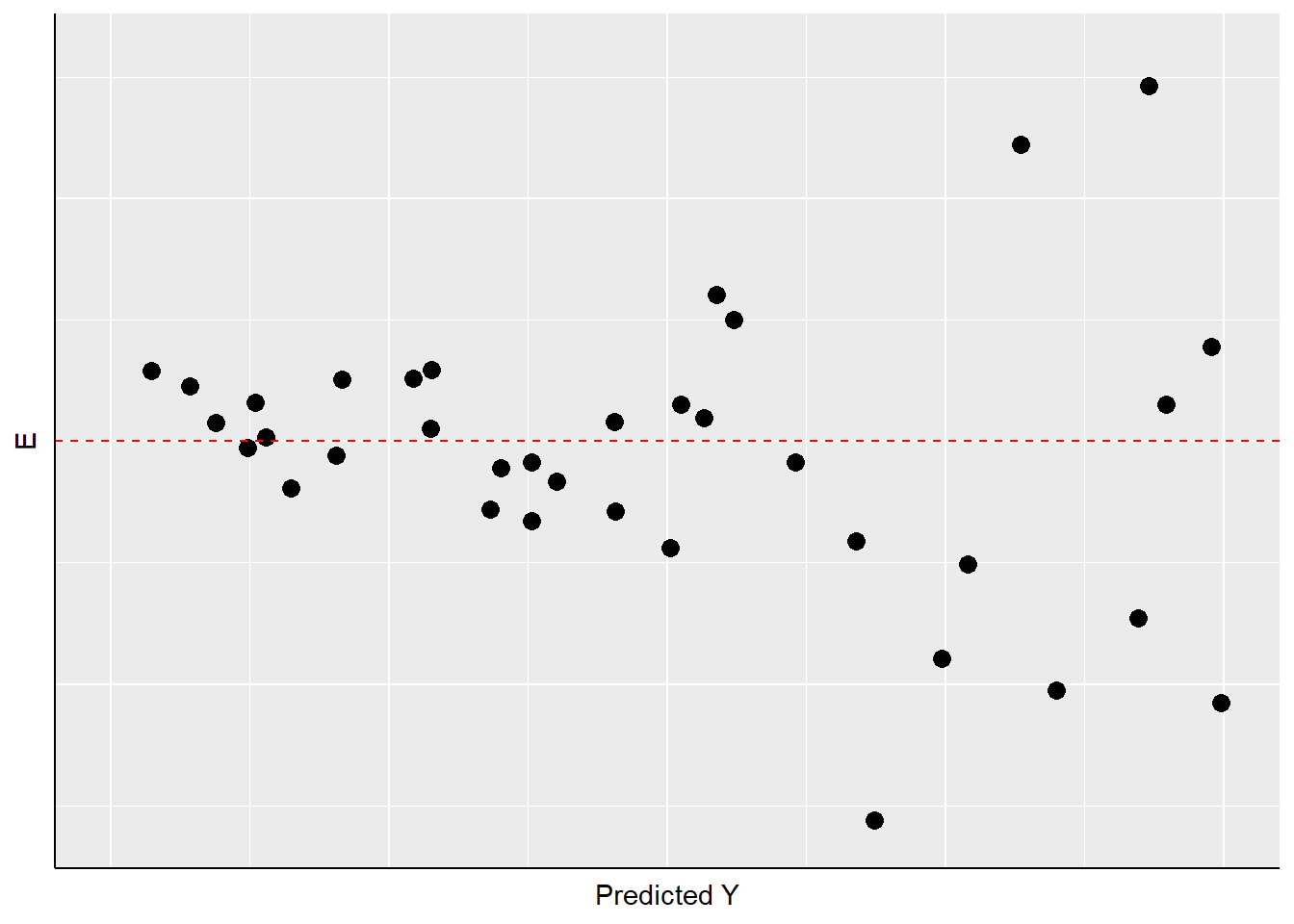
Como\(\PageIndex{5}\) muestra la Figura, el ancho de la dispersión de los residuos crece a medida que aumenta el valor predicho de YY, haciendo un patrón en forma de abanico. Igualmente inquietante sería el caso de un “abanico inverso”, o un patrón con una protuberancia en el medio y distribuciones muy “apretadas” de residuos en cualquier extremo. Todos estos serían casos en los que falla la suposición de varianza constante en los residuos (o “homocedasticidad”), y son referidos como instancias de heterocedasticidad.
¿Cuáles son las implicaciones de la heterocedasticidad? Nuestras pruebas de hipótesis para los coeficientes estimados (AA y BB) se basan en el supuesto de que los errores estándar de las estimaciones (ver capítulo anterior) se distribuyen normalmente. Si la inspección de sus residuos proporciona evidencia para cuestionar esa suposición, entonces la interpretación de los valores t y los valores p puede ser problemática. Intuitivamente, en tal caso la precisión de nuestras estimaciones de AA y BB no son constantes, sino que dependerán del valor predicho de YY. Entonces podrías estar estimando BB con relativa precisión en algunos rangos de YY, y menos precisos en otros. Eso significa que no puedes depender de los valores t y p estimados para probar tus hipótesis.
10.2.3 No linealidad en los parámetros
Uno de los supuestos principales de la regresión simple de OLS es que el parámetro de pendiente estimado (el BB) será constante, y por lo tanto el modelo será lineal. Dicho de otra manera, el efecto de cualquier cambio en XX sobre YY debe ser constante en el rango de YY. Así, si nuestra suposición es correcta, el patrón de los residuales debe ser aproximadamente simétrico, por encima y por debajo de cero, sobre el rango de valores predichos.
Si la relación real entre XX y YY no es lineal, sin embargo, los valores predichos (lineales) para YY se apartarán sistemáticamente de la relación (curva) que se representa en los datos. La figura\(\PageIndex{6}\) muestra el tipo de patrón que esperaríamos en nuestros residuales si la relación observada entre XX e YY es una curva fuerte cuando intentamos modelarla como si fuera lineal.
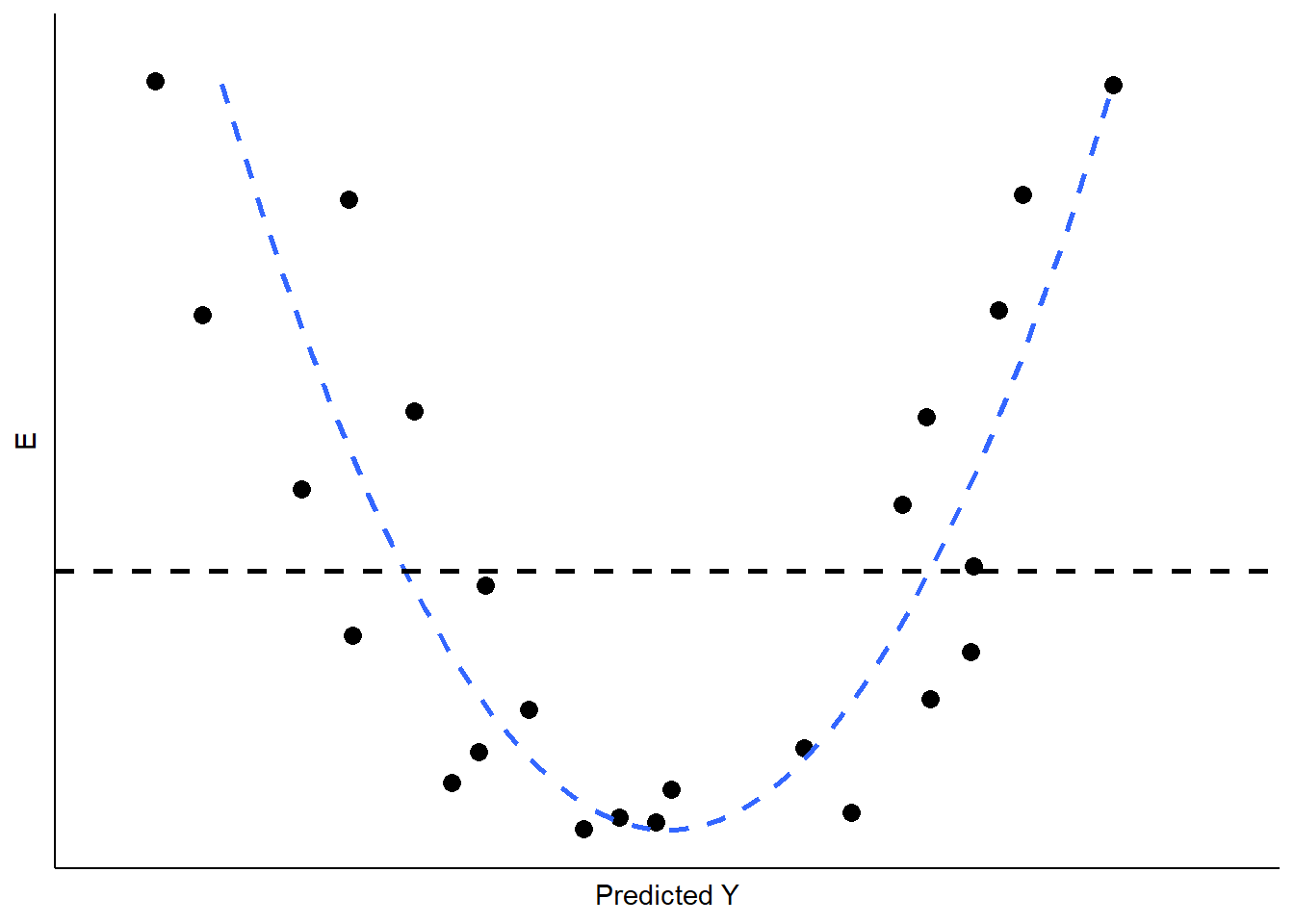
¿Cuáles son las implicaciones de la no linealidad? Primero, debido a que la pendiente no es constante, la estimación de BB será sesgada. En la ilustración mostrada en la Figura\(\PageIndex{6}\), BB subestimaría el valor de YY tanto en el rango bajo como en el alto del valor predicho de YY, y lo sobreestimaría en el rango medio. Además, los errores estándar de los residuos serán grandes, debido a la sobreestimación sistemática de YY, haciendo que el modelo sea muy ineficiente (o impreciso).


