2.7: La asimetría y la media, mediana y modo
- Page ID
- 153245
Considera el siguiente conjunto de datos.
4; 5; 6; 6; 6; 7; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 10
Este conjunto de datos puede ser representado por el siguiente histograma. Cada intervalo tiene ancho uno, y cada valor se ubica en medio de un intervalo.
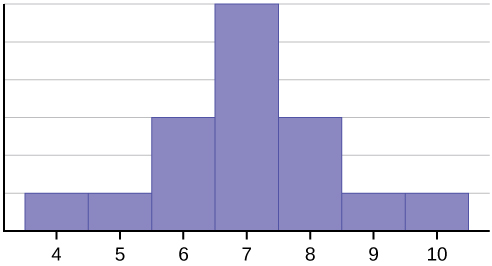
El histograma muestra una distribución simétrica de datos. Una distribución es simétrica si se puede dibujar una línea vertical en algún punto del histograma de tal manera que la forma a la izquierda y la derecha de la línea vertical sean imágenes especulares entre sí. La media, la mediana y el modo son cada uno siete para estos datos. En una distribución perfectamente simétrica, la media y la mediana son las mismas. Este ejemplo tiene un modo (unimodal), y el modo es el mismo que la media y la mediana. En una distribución simétrica que tiene dos modos (bimodal), los dos modos serían diferentes de la media y la mediana.
El histograma para los datos: 4; 5; 6; 6; 6; 7; 7; 7; 8 no es simétrico. El lado derecho parece “picado” en comparación con el lado izquierdo. Una distribución de este tipo se llama sesgada a la izquierda porque se saca hacia la izquierda.
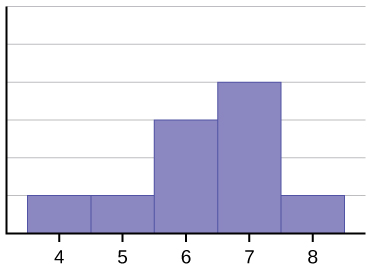
La media es 6.3, la mediana es 6.5 y el modo es siete. Observe que la media es menor que la mediana, y ambas son menores que el modo. Tanto la media como la mediana reflejan el sesgo, pero la media lo refleja más.
El histograma para los datos: 6; 7; 7; 7; 7; 8; 8; 8; 9; 10, tampoco es simétrico. Está sesgada a la derecha.
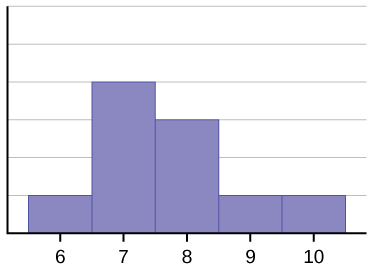
La media es 7.7, la mediana es 7.5 y el modo es siete. De las tres estadísticas, la media es la mayor, mientras que la modalidad es la más pequeña. Nuevamente, la media refleja más el sesgo.
Generalmente, si la distribución de los datos está sesgada hacia la izquierda, la media es menor que la mediana, que suele ser menor que el modo. Si la distribución de los datos está sesgada hacia la derecha, el modo suele ser menor que la mediana, que es menor que la media.
La asimetría y la simetría adquieren importancia cuando discutimos las distribuciones de probabilidad en capítulos posteriores.
Ejemplo\(\PageIndex{1}\)
Las estadísticas se utilizan para comparar y en ocasiones identificar a los autores. Las siguientes listas muestran una muestra aleatoria simple que compara los recuentos de letras de tres autores.
- Terry: 7; 9; 3; 3; 3; 4; 1; 3; 2; 2
- Davis: 3; 3; 3; 4; 1; 4; 3; 3; 2; 3; 1
- Maris: 2; 3; 4; 4; 4; 6; 6; 6; 8; 3
- Haz una gráfica de puntos para los tres autores y compara las formas.
- Calcular la media para cada uno.
- Calcular la mediana para cada uno.
- Describe cualquier patrón que notes entre la forma y las medidas del centro.
Solución
-
Figura\(\PageIndex{4}\): La distribución de Terry tiene un sesgo correcto (positivo).
Figura\(\PageIndex{5}\): La distribución de Davis tiene un sesgo izquierdo (negativo)
Figura\(\PageIndex{6}\): La distribución de Maris tiene forma simétrica.
- La media de Terry es 3.7, la media de Davis es 2.7, la media de Maris es 4.6.
- La mediana de Terry es tres, la mediana de Davis es tres. La mediana de Maris es de cuatro.
- Parece que la mediana siempre está más cerca del punto alto (el modo), mientras que la media tiende a estar más alejada en la cola. En una distribución simétrica, la media y la mediana están ubicadas centralmente cerca del punto alto de la distribución.
Ejercicio\(\PageIndex{1}\)
Discutir la media, mediana y modo para cada uno de los siguientes problemas. ¿Hay un patrón entre la forma y la medida del centro?
a.

b.
| The Ages Murieron ex presidentes de Estados Unidos | |
|---|---|
| 4 | 6 9 |
| 5 | 3 6 7 7 7 8 |
| 6 | 0 0 3 3 4 4 5 6 7 7 7 8 |
| 7 | 0 1 1 2 3 4 7 8 8 9 |
| 8 | 0 1 3 5 8 |
| 9 | 0 0 3 |
| Clave: 8|0 significa 80. | |
c.

Revisar
Observar la distribución de los datos puede revelar mucho sobre la relación entre la media, la mediana y el modo. Hay tres tipos de distribuciones. Una distribución sesgada izquierda (o negativa) tiene una forma como Figura\(\PageIndex{2}\). Una distribución sesgada derecha (o positiva) tiene una forma como Figura\(\PageIndex{3}\). Una distribución simétrica se parece a Figura\(\PageIndex{1}\).
Utilice la siguiente información para responder a los siguientes tres ejercicios: Determine si los datos son simétricos, sesgados a la izquierda o sesgados a la derecha.
Ejercicio 2.7.2
1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5
Contestar
Los datos son simétricos. La mediana es 3 y la media es 2.85. Están cerca, y el modo se encuentra cerca de la mitad de los datos, por lo que los datos son simétricos.
Ejercicio 2.7.3
16; 17; 19; 22; 22; 22; 22; 22; 23
Ejercicio 2.7.4
87; 87; 87; 87; 87; 88; 89; 89; 90; 91
Contestar
Los datos están sesgados a la derecha. La mediana es de 87.5 y la media es de 88.2. A pesar de que están cerca, el modo se encuentra a la izquierda de la mitad de los datos, y hay muchas más instancias de 87 que cualquier otro número, por lo que los datos están sesgados a la derecha.
Ejercicio 2.7.5
Cuando los datos están sesgados a la izquierda, ¿cuál es la relación típica entre la media y la mediana?
Ejercicio 2.7.6
Cuando los datos son simétricos, ¿cuál es la relación típica entre la media y la mediana?
Contestar
Cuando los datos son simétricos, la media y la mediana son cercanas o iguales.
Ejercicio 2.7.7
¿Qué palabra describe una distribución que tiene dos modos?
Ejercicio 2.7.8
Describir la forma de esta distribución.

Contestar
La distribución está sesgada a la derecha porque parece sacada a la derecha.
Ejercicio 2.7.9
Describir la relación entre el modo y la mediana de esta distribución.

Ejercicio 2.7.10
Describir la relación entre la media y la mediana de esta distribución.

Contestar
La media es 4.1 y es ligeramente mayor que la mediana, que es cuatro.
Ejercicio 2.7.11
Describir la forma de esta distribución.

Ejercicio 2.7.12
Describir la relación entre el modo y la mediana de esta distribución.

Contestar
El modo y la mediana son los mismos. En este caso, ambos son cinco.
Ejercicio 2.7.13
¿La media y la mediana son exactamente iguales en esta distribución? ¿Por qué o por qué no?

Ejercicio 2.7.14
Describir la forma de esta distribución.

Contestar
La distribución está sesgada a la izquierda porque parece sacada a la izquierda.
Ejercicio 2.7.15
Describir la relación entre el modo y la mediana de esta distribución.

Ejercicio 2.7.16
Describir la relación entre la media y la mediana de esta distribución.

Contestar
La media y la mediana son ambas seis.
Ejercicio 2.7.17
La media y la mediana para los datos son las mismas.
3; 4; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 7
¿Los datos son perfectamente simétricos? ¿Por qué o por qué no?
Ejercicio 2.7.18
¿Cuál es el mayor, la media, el modo o la mediana del conjunto de datos?
11; 11; 12; 12; 12; 12; 13; 15; 17; 22; 22; 22
Contestar
El modo es 12, la mediana es 12.5 y la media es 15.1. La media es la más grande.
Ejercicio 2.7.19
¿Cuál es la menor, la media, el modo y la mediana del conjunto de datos?
56; 56; 56; 58; 59; 60; 62; 64; 64; 65; 67
Ejercicio 2.7.20
De las tres medidas, que tiende a reflejar más sesgo, ¿la media, la modalidad o la mediana? ¿Por qué?
Contestar
La media tiende a reflejar el sesgo más porque es la que más se ve afectada por los valores atípicos.
Ejercicio 2.7.21
En una distribución perfectamente simétrica, ¿cuándo sería diferente el modo de la media y la mediana?


