2.8: Medidas de la difusión de los datos
- Page ID
- 153228
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Una característica importante de cualquier conjunto de datos es la variación en los datos. En algunos conjuntos de datos, los valores de datos se concentran estrechamente cerca de la media; en otros conjuntos de datos, los valores de datos están más extensamente dispersos a partir de la media. La medida más común de variación, o spread, es la desviación estándar. La desviación estándar es un número que mide qué tan lejos están los valores de los datos de su media.
La desviación estándar
- proporciona una medida numérica de la cantidad total de variación en un conjunto de datos, y
- se puede utilizar para determinar si un valor de datos en particular está cerca o lejos de la media.
La desviación estándar proporciona una medida de la variación general en un conjunto de datos
La desviación estándar es siempre positiva o cero. La desviación estándar es pequeña cuando todos los datos están concentrados cerca de la media, mostrando poca variación o dispersión. La desviación estándar es mayor cuando los valores de los datos están más dispersos de la media, exhibiendo más variación.
Supongamos que estamos estudiando la cantidad de tiempo que los clientes esperan en la fila en la caja en el supermercado A y el supermercado B. el tiempo promedio de espera en ambos supermercados es de cinco minutos. En el supermercado A, la desviación estándar para el tiempo de espera es de dos minutos; en el supermercado B la desviación estándar para el tiempo de espera es de cuatro minutos.
Debido a que el supermercado B tiene una desviación estándar más alta, sabemos que hay más variación en los tiempos de espera en el supermercado B. En general, los tiempos de espera en el supermercado B están más dispersos del promedio; los tiempos de espera en el supermercado A están más concentrados cerca de la media.
La desviación estándar se puede utilizar para determinar si un valor de datos está cerca o lejos de la media.
Supongamos que Rosa y Binh hacen compras en el supermercado A. Rosa espera siete minutos en el mostrador de caja y Binh espera un minuto. En el supermercado A, el tiempo medio de espera es de cinco minutos y la desviación estándar es de dos minutos. La desviación estándar se puede utilizar para determinar si un valor de datos está cerca o lejos de la media.
Rosa espera siete minutos:
- Siete es dos minutos más largo que el promedio de cinco; dos minutos es igual a una desviación estándar.
- El tiempo de espera de Rosa de siete minutos es dos minutos más largo que el promedio de cinco minutos.
- El tiempo de espera de Rosa de siete minutos es una desviación estándar por encima del promedio de cinco minutos.
Binh espera un minuto.
- Uno es cuatro minutos menos que el promedio de cinco; cuatro minutos equivale a dos desviaciones estándar.
- El tiempo de espera de Binh de un minuto es cuatro minutos menos que el promedio de cinco minutos.
- El tiempo de espera de Binh de un minuto es de dos desviaciones estándar por debajo del promedio de cinco minutos.
- Un valor de datos que es dos desviaciones estándar del promedio está justo en el límite para lo que muchos estadísticos considerarían que está lejos del promedio. Considerar que los datos están lejos de la media si están a más de dos desviaciones estándar de distancia es más una “regla general” aproximada que una regla rígida. En general, la forma de la distribución de los datos afecta la cantidad de datos que se encuentra más lejos que dos desviaciones estándar. (Aprenderás más sobre esto en capítulos posteriores.)
La línea numérica puede ayudarle a entender la desviación estándar. Si tuviéramos que poner cinco y siete en una línea numérica, siete está a la derecha de cinco. Decimos, entonces, que siete es una desviación estándar a la derecha de cinco porque\(5 + (1)(2) = 7\).
Si uno también formara parte del conjunto de datos, entonces uno es dos desviaciones estándar a la izquierda de cinco porque\(5 + (-2)(2) = 1\).

- En general, un valor = media + (#ofSTDEV) (desviación estándar)
- donde #ofSTDEVs = el número de desviaciones estándar
- #ofSTDEV no necesita ser un entero
- Una son dos desviaciones estándar menores que la media de cinco porque:\(1 = 5 + (-2)(2)\).
El valor de la ecuación = media + (#ofSTDEVs) (desviación estándar) se puede expresar para una muestra y para una población.
- muestra:\[x = \bar{x} + \text{(#ofSTDEV)(s)}\]
- Población:\[x = \mu + \text{(#ofSTDEV)(s)}\]
La letra minúscula s representa la desviación estándar de la muestra y la letra griega\(\sigma\) (sigma, minúscula) representa la desviación estándar de la población.
El símbolo\(\bar{x}\) es la media muestral y el símbolo griego\(\mu\) es la media poblacional.
Cálculo de la desviación estándar
Si\(x\) es un número, entonces la diferencia "\(x\)— media” se llama su desviación. En un conjunto de datos, hay tantas desviaciones como elementos en el conjunto de datos. Las desviaciones se utilizan para calcular la desviación estándar. Si los números pertenecen a una población, en símbolos es una desviación\(x - \mu\). Para los datos de muestra, en símbolos una desviación es\(x - \bar{x}\).
El procedimiento para calcular la desviación estándar depende de si los números son toda la población o son datos de una muestra. Los cálculos son similares, pero no idénticos. Por lo tanto, el símbolo utilizado para representar la desviación estándar depende de si se calcula a partir de una población o de una muestra. La letra minúscula s representa la desviación estándar de la muestra y la letra griega\(\sigma\) (sigma, minúscula) representa la desviación estándar de la población. Si la muestra tiene las mismas características que la población, entonces s debe ser una buena estimación de\(\sigma\).
Para calcular la desviación estándar, primero necesitamos calcular la varianza. La varianza es el promedio de los cuadrados de las desviaciones (los\(x - \bar{x}\) valores para una muestra, o los\(x - \mu\) valores para una población). El símbolo\(\sigma^{2}\) representa la varianza poblacional; la desviación estándar poblacional\(\sigma\) es la raíz cuadrada de la varianza poblacional. El símbolo\(s^{2}\) representa la varianza muestral; la desviación estándar muestral s es la raíz cuadrada de la varianza muestral. Se puede pensar en la desviación estándar como un promedio especial de las desviaciones.
Si los números provienen de un censo de toda la población y no de una muestra, cuando calculamos el promedio de las desviaciones cuadradas para encontrar la varianza, dividimos por\(N\), el número de ítems en la población. Si los datos son de una muestra más que de una población, cuando calculamos el promedio de las desviaciones cuadradas, dividimos por n — 1, uno menos que el número de ítems en la muestra.
Fórmulas para la desviación estándar de la muestra
\[s = \sqrt{\dfrac{\sum(x-\bar{x})^{2}}{n-1}} \label{eq1}\]
o
\[s = \sqrt{\dfrac{\sum f (x-\bar{x})^{2}}{n-1}} \label{eq2}\]
Para la desviación estándar de la muestra, el denominador es\(n - 1\), es decir, el tamaño muestral MENOS 1.
Fórmulas para la desviación estándar de la población
\[\sigma = \sqrt{\dfrac{\sum(x-\mu)^{2}}{N}} \label{eq3} \]
o
\[\sigma = \sqrt{\dfrac{\sum f (x-\mu)^{2}}{N}} \label{eq4}\]
Para la desviación estándar poblacional, el denominador es\(N\), el número de ítems en la población.
En Ecuaciones\ ref {eq2} y\ ref {eq4},\(f\) representa la frecuencia con la que aparece un valor. Por ejemplo, si un valor aparece una vez,\(f\) es uno. Si un valor aparece tres veces en el conjunto de datos o población,\(f\) es tres.
Variabilidad de muestreo de un estadístico
El estadístico de una distribución muestral se discutió en la Sección 2.6. Cuánto varía el estadístico de una muestra a otra se conoce como variabilidad muestral de un estadístico. Normalmente se mide la variabilidad de muestreo de un estadístico por su error estándar.
El error estándar de la media es un ejemplo de un error estándar. Es una desviación estándar especial y se conoce como la desviación estándar de la distribución muestral de la media. Cubrirás el error estándar de la media en el Capítulo 7. La notación para el error estándar de la media es\(\dfrac{\sigma}{\sqrt{n}}\) donde\(\sigma\) está la desviación estándar de la población y\(n\) es el tamaño de la muestra.
En la práctica, utilice una calculadora o software informático para calcular la desviación estándar. Si está utilizando una calculadora TI-83, 83+, 84+, debe seleccionar la desviación estándar adecuada\(\sigma_{x}\) o \(s_{x}\)de las estadísticas resumidas. Nos concentraremos en usar e interpretar la información que nos da la desviación estándar. Sin embargo, debes estudiar el siguiente ejemplo paso a paso para ayudarte a entender cómo la desviación estándar mide la variación de la media. (Las instrucciones de la calculadora aparecen al final de este ejemplo).
Ejemplo\(\PageIndex{1}\)
En una clase de quinto grado, la maestra se interesó por la edad promedio y la desviación estándar muestral de las edades de sus alumnos. Los siguientes datos son las edades para una MUESTRA de n = 20 estudiantes de quinto grado. Las edades se redondean al medio año más cercano:
9; 9.5; 9.5; 10; 10; 10; 10.5; 10.5; 10.5; 10.5; 10.5; 11; 11; 11; 11; 11; 11.5; 11.5; 11.5; 11.5; 11.5;
\[\bar{x} = \dfrac{9+9.5(2)+10(4)+10.5(4)+11(6)+11.5(3)}{20} = 10.525 \nonumber\]
La edad promedio es de 10.53 años, redondeada a dos lugares.
La varianza se puede calcular usando una tabla. Después se calcula la desviación estándar tomando la raíz cuadrada de la varianza. Vamos a explicar las partes de la tabla después de calcular s.
| Datos | Freq. | Desviaciones | Desviaciones 2 | (Freq.) (Desviaciones 2) |
|---|---|---|---|---|
| x | f | (x —\(\bar{x}\)) | (x —\(\bar{x}\)) 2 | f) (x —\(\bar{x}\)) 2 |
| 9 | 1 | 9 — 10.525 = —1.525 | (—1.525) 2 = 2.325625 | 1 × 2.325625 = 2.325625 |
| 9.5 | 2 | 9.5 — 10.525 = —1.025 | (—1.025) 2 = 1,050625 | 2 × 1.050625 = 2.101250 |
| 10 | 4 | 10 — 10.525 = —0.525 | (—0.525) 2 = 0.275625 | 4 × 0.275625 = 1.1025 |
| 10.5 | 4 | 10.5 — 10.525 = —0.025 | (—0.025) 2 = 0.000625 | 4 × 0.000625 = 0.0025 |
| 11 | 6 | 11 — 10.525 = 0.475 | (0.475) 2 = 0.225625 | 6 × 0.225625 = 1.35375 |
| 11.5 | 3 | 11.5 — 10.525 = 0.975 | (0.975) 2 = 0.950625 | 3 × 0.950625 = 2.851875 |
| El total es 9.7375 |
La varianza muestral\(s^{2}\),, es igual a la suma de la última columna (9.7375) dividida por el número total de valores de datos menos uno (20 — 1):
\[s^{2} = \dfrac{9.7375}{20-1} = 0.5125 \nonumber\]
La desviación estándar muestra s es igual a la raíz cuadrada de la varianza de la muestra:
\[s = \sqrt{0.5125} = 0.715891 \nonumber\]
y esto se redondea a dos decimales,\(s = 0.72\).
Normalmente, haces el cálculo de la desviación estándar en tu calculadora o computadora. Los resultados intermedios no son redondeados. Esto se hace para mayor precisión.
- Para los siguientes problemas, recordemos ese valor = media + (#ofSTDEVs) (desviación estándar). Verificar la media y desviación estándar o una calculadora o computadora.
- Para una muestra:\(x\) =\(\bar{x}\) + (#ofSTDEVs) (s)
- Para una población:\(x\) =\(\mu\) + (#ofSTDEVs)\(\sigma\)
- Para este ejemplo, use x =\(\bar{x}\) + (#ofSTDEVs) (s) porque los datos son de una muestra
- Verifica la media y la desviación estándar en tu calculadora o computadora.
- Encuentra el valor que es una desviación estándar por encima de la media. Encuentra (\(\bar{x}\)+ 1s).
- Encuentra el valor que es dos desviaciones estándar por debajo de la media. Encuentra (\(\bar{x}\)— 2s).
- Encuentra los valores que son 1.5 desviaciones estándar de (por debajo y por encima) de la media.
Solución
-
- Listas claras L1 y L2. Presione STAT 4:CLRList. Ingrese 2nd 1 para L1, la coma (,) y 2nd 2 para L2.
- Ingresa datos en el editor de listas. Presione STAT 1:EDIT. Si es necesario, borre las listas con flechas hacia arriba en el nombre. Presiona CLEAR y flecha hacia abajo.
- Ponga los valores de datos (9, 9.5, 10, 10.5, 11, 11.5) en la lista L1 y las frecuencias (1, 2, 4, 4, 6, 3) en la lista L2. Usa las teclas de flecha para moverte.
- Presione STAT y flecha hacia CALC. Presione 1:1 -VarStats e ingrese L1 (2nd 1), L2 (2nd 2). No olvides la coma. Presione ENTER.
- \(\bar{x}\)= 10.525
- Use Sx porque se trata de datos de muestra (no una población): Sx=0.715891
- (\(\bar{x} + 1s) = 10.53 + (1)(0.72) = 11.25\)
- \((\bar{x} - 2s) = 10.53 – (2)(0.72) = 9.09\)
-
- \((\bar{x} - 1.5s) = 10.53 – (1.5)(0.72) = 9.45\)
- \((\bar{x} + 1.5s) = 10.53 + (1.5)(0.72) = 11.61\)
Ejercicio 2.8.1
En un equipo de béisbol, las edades de cada uno de los jugadores son las siguientes:
21; 21; 22; 23; 24; 24; 25; 25; 28; 29; 29; 31; 32; 33; 33; 34; 35; 36; 36; 36; 36; 38; 38; 40
Usa tu calculadora o computadora para encontrar la media y la desviación estándar. Después encuentra el valor que es dos desviaciones estándar por encima de la media.
Contestar
\(\mu\)= 30.68
\(s = 6.09\)
(\(\bar{x} + 2s = 30.68 + (2)(6.09) = 42.86\).
Explicación del cálculo de la desviación estándar que se muestra en la tabla
Las desviaciones muestran cuán dispersos están los datos sobre la media. El valor de datos 11.5 está más alejado de la media que el valor de datos 11 que se indica por las desviaciones 0.97 y 0.47. Una desviación positiva ocurre cuando el valor de los datos es mayor que la media, mientras que una desviación negativa ocurre cuando el valor de los datos es menor que la media. La desviación es —1.525 para el valor de datos nueve. Si agrega las desviaciones, la suma siempre es cero. (Por ejemplo\(\PageIndex{1}\), hay\(n = 20\) desviaciones.) Por lo que no se puede simplemente agregar las desviaciones para obtener el spread de los datos. Al cuadrar las desviaciones, los haces números positivos, y la suma también será positiva. La varianza, entonces, es la desviación cuadrada promedio.
La varianza es una medida cuadrada y no tiene las mismas unidades que los datos. Tomar la raíz cuadrada resuelve el problema. La desviación estándar mide el spread en las mismas unidades que los datos.
Observe que en lugar de dividir por\(n = 20\), el cálculo se divide por\(n - 1 = 20 - 1 = 19\) porque los datos son una muestra. Para la varianza muestral, dividimos por el tamaño de la muestra menos uno (\(n - 1\)). ¿Por qué no dividir por\(n\)? La respuesta tiene que ver con la varianza poblacional. La varianza muestral es una estimación de la varianza poblacional. Con base en las matemáticas teóricas que se encuentran detrás de estos cálculos, dividir por (\(n - 1\)) da una mejor estimación de la varianza poblacional.
Tu concentración debe estar en lo que nos dice la desviación estándar sobre los datos. La desviación estándar es un número que mide hasta qué punto se distribuyen los datos de la media. Deje que una calculadora o computadora haga la aritmética.
La desviación estándar,\(s\) o\(\sigma\), es cero o mayor que cero. Cuando la desviación estándar es cero, no hay spread; es decir, todos los valores de datos son iguales entre sí. La desviación estándar es pequeña cuando todos los datos están concentrados cerca de la media, y es mayor cuando los valores de los datos muestran más variación de la media. Cuando la desviación estándar es mucho mayor que cero, los valores de los datos están muy dispersos sobre la media; los valores atípicos pueden hacer\(s\) o\(\sigma\) muy grandes.
La desviación estándar, cuando se presenta por primera vez, puede parecer poco clara. Al graficar sus datos, puede obtener una mejor “sensación” de las desviaciones y la desviación estándar. Encontrarás que en distribuciones simétricas, la desviación estándar puede ser muy útil pero en distribuciones sesgadas, la desviación estándar puede no ser de mucha ayuda. La razón es que los dos lados de una distribución sesgada tienen diferenciales diferentes. En una distribución sesgada, es mejor mirar el primer cuartil, la mediana, el tercer cuartil, el valor más pequeño y el valor más grande. Debido a que los números pueden ser confusos, siempre grafica tus datos. Muestre sus datos en un histograma o una gráfica de caja.
Ejemplo\(\PageIndex{2}\)
Utilice los siguientes datos (puntajes de los primeros exámenes) de la clase de pre-cálculo de primavera de Susan Dean:
33; 42; 49; 49; 53; 55; 55; 61; 63; 67; 68; 68; 69; 69; 72; 73; 74; 78; 80; 83; 88; 88; 88; 90; 92; 94; 94; 94; 94; 94; 94; 96; 100
- Cree un gráfico que contenga los datos, frecuencias, frecuencias relativas y frecuencias relativas acumuladas a tres decimales.
- Calcule lo siguiente a un decimal usando una calculadora TI-83+ o TI-84:
- La media de la muestra
- La desviación estándar de la muestra
- La mediana
- El primer cuartil
- El tercer cuartil
- IQR
- Construir una gráfica de caja y un histograma en el mismo conjunto de ejes. Haga comentarios sobre la gráfica de caja, el histograma y el gráfico.
Contestar
- Ver Tabla
-
- La media muestral = 73.5
- La desviación estándar de la muestra = 17.9
- La mediana = 73
- El primer cuartil = 61
- El tercer cuartil = 90
- IQR = 90 — 61 = 29
- El\(x\) eje -va de 32.5 a 100.5;\(y\) -eje va de -2.4 a 15 para el histograma. El número de intervalos es cinco, por lo que el ancho de un intervalo es (\(100.5 - 32.5\)) dividido por cinco, es igual a 13.6. Los puntos finales de los intervalos son los siguientes: el punto de partida es 32.5,,\(32.5 + 13.6 = 46.1\),\(46.1 + 13.6 = 59.7\),\(59.7 + 13.6 = 73.3\),\(73.3 + 13.6 = 86.9\),\(86.9 + 13.6 = 100.5 =\) el valor final; Ningún valor de datos cae en un límite de intervalo.
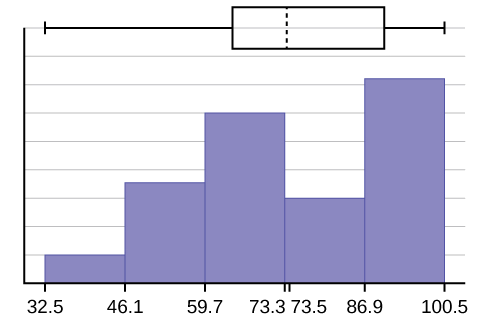
El bigote largo izquierdo en la gráfica de caja se refleja en el lado izquierdo del histograma. El esparcimiento de las puntuaciones de los exámenes en el 50% inferior es mayor (\(73 - 33 = 40\)) que el diferencial en el 50% superior (\(100 - 73 = 27\)). El histograma, la gráfica de caja y la gráfica reflejan esto. Hay un número sustancial de grados A y B (80, 90 y 100). El histograma lo muestra claramente. La trama de caja nos muestra que el 50% medio de las puntuaciones de los exámenes (IQR = 29) son Ds, Cs y Bs. La trama de caja también nos muestra que el 25% más bajo de los puntajes de los exámenes son Ds y Fs.
| Datos | Frecuencia | Frecuencia relativa | Frecuencia Relativa Acumulada |
|---|---|---|---|
| 33 | 1 | 0.032 | 0.032 |
| 42 | 1 | 0.032 | 0.064 |
| 49 | 2 | 0.065 | 0.129 |
| 53 | 1 | 0.032 | 0.161 |
| 55 | 2 | 0.065 | 0.226 |
| 61 | 1 | 0.032 | 0.258 |
| 63 | 1 | 0.032 | 0.29 |
| 67 | 1 | 0.032 | 0.322 |
| 68 | 2 | 0.065 | 0.387 |
| 69 | 2 | 0.065 | 0.452 |
| 72 | 1 | 0.032 | 0.484 |
| 73 | 1 | 0.032 | 0.516 |
| 74 | 1 | 0.032 | 0.548 |
| 78 | 1 | 0.032 | 0.580 |
| 80 | 1 | 0.032 | 0.612 |
| 83 | 1 | 0.032 | 0.644 |
| 88 | 3 | 0.097 | 0.741 |
| 90 | 1 | 0.032 | 0.773 |
| 92 | 1 | 0.032 | 0.805 |
| 94 | 4 | 0.129 | 0.934 |
| 96 | 1 | 0.032 | 0.966 |
| 100 | 1 | 0.032 | 0.998 (¿Por qué este valor no es 1?) |
Ejercicio\(\PageIndex{2}\)
Los siguientes datos muestran los diferentes tipos de tiendas de alimentos para mascotas en la zona llevan.
6; 6; 6; 6; 7; 7; 7; 7; 7; 8; 9; 9; 9; 9; 9; 10; 10; 10; 10; 10; 10; 11; 11; 11; 11; 12; 12; 12; 12; 12; 12;
Calcular la media de la muestra y la desviación estándar de la muestra a un decimal usando una calculadora TI-83+ o TI-84.
Contestar
\(\mu = 9.3\)y\(s = 2.2\)
Desviación estándar de tablas de frecuencias agrupadas
Recordemos que para los datos agrupados no conocemos valores de datos individuales, por lo que no podemos describir con precisión el valor típico de los datos. En otras palabras, no podemos encontrar la media exacta, mediana o modo. Podemos, sin embargo, determinar la mejor estimación de las medidas de centro encontrando la media de los datos agrupados con la fórmula:
\[\text{Mean of Frequency Table} = \dfrac{\sum fm}{\sum f}\]
donde frecuencias\(f\) de\(m =\) intervalo y puntos medios de intervalo.
Así como no pudimos encontrar la media exacta, tampoco podemos encontrar la desviación estándar exacta. Recuerde que la desviación estándar describe numéricamente la desviación esperada que tiene un valor de datos de la media. En inglés simple, la desviación estándar nos permite comparar cuán “inusuales” se comparan los datos individuales con la media.
Ejemplo\(\PageIndex{3}\)
Encuentra la desviación estándar para los datos en la Tabla\(\PageIndex{3}\).
| Clase | Frecuencia, f | Punto medio, m | m 2 | \(\bar{x}\) | fm 2 | Desviación estándar |
|---|---|---|---|---|---|---|
| 0—2 | 1 | 1 | 1 | \ (\ bar {x}\)” style="vertical-align:middle; ">7.58 | 1 | 3.5 |
| 3—5 | 6 | 4 | 16 | \ (\ bar {x}\)” style="vertical-align:middle; ">7.58 | 96 | 3.5 |
| 6—8 | 10 | 7 | 49 | \ (\ bar {x}\)” style="vertical-align:middle; ">7.58 | 490 | 3.5 |
| 9—11 | 7 | 10 | 100 | \ (\ bar {x}\)” style="vertical-align:middle; ">7.58 | 700 | 3.5 |
| 12—14 | 0 | 13 | 169 | \ (\ bar {x}\)” style="vertical-align:middle; ">7.58 | 0 | 3.5 |
| 15—17 | 2 | 16 | 256 | \ (\ bar {x}\)” style="vertical-align:middle; ">7.58 | 512 | 3.5 |
Para este conjunto de datos, tenemos la media,\(\bar{x}\) = 7.58 y la desviación estándar,\(s_{x}\) = 3.5. Esto significa que se esperaría que un valor de datos seleccionado aleatoriamente fuera de 3.5 unidades de la media. Si nos fijamos en la primera clase, vemos que el punto medio de la clase es igual a uno. Se trata de casi dos desviaciones estándar completas de la media desde 7.58 — 3.5 — 3.5 = 0.58. Si bien la fórmula para calcular la desviación estándar no es complicada,\(s_{x} = \sqrt{\dfrac{f(m - \bar{x})^{2}}{n-1}}\) donde\(s_{x}\) = desviación estándar de la muestra,\(\bar{x}\) = media de la muestra, los cálculos son tediosos. Por lo general, lo mejor es usar la tecnología al realizar los cálculos.
Encuentra la desviación estándar para los datos del ejemplo anterior
| Clase | 0-2 | 3-5 | 6-8 | 9—11 | 12—14 | 15—17 |
|---|---|---|---|---|---|---|
| Frecuencia, f | 1 | 6 | 10 | 7 | 0 | 2 |
Primero, presione la tecla STAT y seleccione 1:Editar

Ingrese los valores del punto medio en L1 y las frecuencias en L2

Seleccione Estadísticas STAT, CALC y 1:1-Var

Seleccione 2 nd luego 1 luego, 2 nd luego 2 Enter

Verá que se muestra tanto una desviación estándar poblacional,\(\sigma_{x}\), como la desviación estándar de la muestra,\(s_{x}\).
Comparación de valores de diferentes conjuntos de datos
La desviación estándar es útil al comparar valores de datos que provienen de diferentes conjuntos de datos. Si los conjuntos de datos tienen diferentes medias y desviaciones estándar, entonces comparar los valores de datos directamente puede ser engañoso.
- Para cada valor de datos, calcule cuántas desviaciones estándar alejadas de su media es el valor.
- Usa la fórmula: valor = media + (#ofSTDEVs) (desviación estándar); resolver para #ofSTDEVs.
- \(\text{#ofSTDEVs} = \dfrac{\text{value-mean}}{\text{standard deviation}}\)
- Comparar los resultados de este cálculo.
#ofSTDEVs a menudo se llama "z -score”; podemos usar el símbolo\(z\). En símbolos, las fórmulas se convierten en:
| Muestra | \(x = \bar{x} + zs\) | \(z = \dfrac{x - \bar{x}}{s}\) |
| Población | \(x = \mu + z\sigma\) | \(z = \dfrac{x - \mu}{\sigma}\) |
Ejemplo\(\PageIndex{4}\)
Dos alumnos, John y Ali, de diferentes escuelas secundarias, quisieron averiguar quién tenía el mayor promedio de calificaciones en comparación con su escuela. ¿Qué estudiante tuvo el promedio más alto en comparación con su escuela?
| Alumno | GPA | GPA medio escolar | Desviación Estándar Escolar |
|---|---|---|---|
| John | 2.85 | 3.0 | 0.7 |
| Ali | 77 | 80 | 10 |
Contestar
Para cada alumno, determinar cuántas desviaciones estándar (#ofSTDEVs) su GPA está lejos del promedio, para su escuela. Presta mucha atención a las señales al comparar e interpretar la respuesta.
\[z = \text{#ofSTDEVs} = \left(\dfrac{\text{value-mean}}{\text{standard deviation}}\right) = \left(\dfrac{x + \mu}{\sigma}\right) \nonumber\]
Para John,
\[z = \text{#ofSTDEVs} = \left(\dfrac{2.85-3.0}{0.7}\right) = -0.21 \nonumber\]
Para Ali,
\[z = \text{#ofSTDEVs} = (\dfrac{77-80}{10}) = -0.3 \nonumber\]
John tiene el mejor promedio en comparación con su escuela porque su promedio promedio es de 0.21 desviaciones estándar por debajo de la media de su escuela mientras que el promedio de Ali es 0.3 desviaciones estándar por debajo de la media de su escuela.
La puntuación z de John de —0.21 es mayor que la puntuación z de Ali de —0.3. Para GPA, valores más altos son mejores, por lo que concluimos que John tiene el mejor GPA en comparación con su escuela.
Ejercicio\(\PageIndex{4}\)
Dos nadadoras, Angie y Beth, de diferentes equipos, quisieron averiguar quién tuvo el mejor tiempo para el estilo libre de 50 metros en comparación con su equipo. ¿Qué nadadora tuvo el mejor tiempo en comparación con su equipo?
| Nadador | Tiempo (segundos) | Tiempo Medio del Equipo | Desviación estándar del equipo |
|---|---|---|---|
| Angie | 26.2 | 27.2 | 0.8 |
| Beth | 27.3 | 30.1 | 1.4 |
Contestar
Para Angie:
\[z = \left(\dfrac{26.2-27.2}{0.8}\right) = -1.25 \nonumber\]
Para Beth:
\[z = \left(\dfrac{27.3-30.1}{1.4}\right) = -2 \nonumber\]
Las siguientes listas dan algunos datos que proporcionan un poco más de información sobre lo que nos dice la desviación estándar sobre la distribución de los datos.
Para CUALQUIER conjunto de datos, no importa cuál sea la distribución de los datos:
- Al menos 75% de los datos se encuentran dentro de dos desviaciones estándar de la media.
- Al menos 89% de los datos se encuentran dentro de tres desviaciones estándar de la media.
- Al menos 95% de los datos se encuentran dentro de 4.5 desviaciones estándar de la media.
- Esto se conoce como Regla de Chebyshev.
Para los datos que tienen una distribución en forma de campana y SIMÉTRICA:
- Aproximadamente el 68% de los datos se encuentra dentro de una desviación estándar de la media.
- Aproximadamente el 95% de los datos se encuentran dentro de dos desviaciones estándar de la media.
- Más del 99% de los datos se encuentran dentro de tres desviaciones estándar de la media.
- Esto se conoce como la Regla Empírica.
- Es importante señalar que esta regla sólo se aplica cuando la forma de la distribución de los datos es en forma de campana y simétrica. Aprenderemos más sobre esto al estudiar la distribución de probabilidad “Normal” o “Gaussiana” en capítulos posteriores.
Referencias
- Datos de Microsoft Bookshelf.
- Rey, Bill. “Gráficamente hablando”. Investigación Institucional, Lake Tahoe Community College. Disponible en línea en www.ltcc.edu/web/about/institucional-research (consultado el 3 de abril de 2013).
Revisar
La desviación estándar puede ayudarle a calcular la propagación de los datos. Existen diferentes ecuaciones a utilizar si están calculando la desviación estándar de una muestra o de una población.
- La Desviación Estándar nos permite comparar datos individuales o clases con la media del conjunto de datos numéricamente.
- \(s = \sqrt{\dfrac{\sum(x-\bar{x})^{2}}{n-1}}\)o\(s = \sqrt{\dfrac{\sum f (x-\bar{x})^{2}}{n-1}}\) es la fórmula para calcular la desviación estándar de una muestra. Para calcular la desviación estándar de una población, utilizaríamos la media poblacional,\(\mu\), y la fórmula\(\sigma = \sqrt{\dfrac{\sum(x-\mu)^{2}}{N}}\) o\(\sigma = \sqrt{\dfrac{\sum f (x-\mu)^{2}}{N}}\). f (x − μ) 2 N − − − − − − − − − √.
Revisión de Fórmula
\[s_{x} = \sqrt{\dfrac{\sum fm^{2}}{n} - \bar{x}^2}\]
dónde\(s_{x} \text{sample standard deviation}\) y\(\bar{x} = \text{sample mean}\)
Utilice la siguiente información para responder a los siguientes dos ejercicios: Los siguientes datos son las distancias entre 20 tiendas minoristas y un gran centro de distribución. Las distancias están en millas.
29; 37; 38; 40; 58; 67; 68; 69; 76; 86; 87; 95; 96; 96; 99; 106; 112; 127; 145; 150
Ejercicio 2.8.4
Use una calculadora gráfica o computadora para encontrar la desviación estándar y redondear a la décima más cercana.
Contestar
\(s\)= 34.5
Ejercicio 2.8.5
Encuentra el valor que es una desviación estándar por debajo de la media.
Ejercicio 2.8.6
Dos beisbolistas, Fredo y Karl, en diferentes equipos quisieron averiguar quién tenía el promedio de bateo más alto en comparación con su equipo. ¿Qué beisbolista tuvo el promedio de bateo más alto en comparación con su equipo?
| Beisbolista | Promedio de bateo | Promedio de bateo por equipos | Desviación estándar del equipo |
|---|---|---|---|
| Fredo | 0.158 | 0.166 | 0.012 |
| Karl | 0.177 | 0.189 | 0.015 |
Contestar
Para Fredo:
\(z\)=\(\dfrac{0.158-0.166}{0.012}\) = —0.67
Para Karl:
\(z\)=\(\dfrac{0.177-0.189}{0.015}\) = —0.8
La puntuación z de Fredo de —0.67 es mayor que la puntuación z de Karl de —0.8. Para el promedio de bateo, los valores más altos son mejores, por lo que Fredo tiene un mejor promedio de bateo en comparación con su equipo.
Ejercicio 2.8.7
Use Tabla para encontrar el valor que es tres desviaciones estándar:
- por encima de la media
- por debajo de la media
Encuentre la desviación estándar para las siguientes tablas de frecuencias usando la fórmula. Consulta los cálculos con el TI 83/84.
Ejercicio 2.8.5
Encuentre la desviación estándar para las siguientes tablas de frecuencias usando la fórmula. Consulta los cálculos con el TI 83/84.
-
Grade Frecuencia 49.5—59.5 2 59.5—69.5 3 69.5—79.5 8 79.5—89.5 12 89.5—99.5 5 -
Baja temperatura diaria Frecuencia 49.5—59.5 53 59.5—69.5 32 69.5—79.5 15 79.5—89.5 1 89.5—99.5 0 -
Puntos por Juego Frecuencia 49.5—59.5 14 59.5—69.5 32 69.5—79.5 15 79.5—89.5 23 89.5—99.5 2
Contestar
- \(s_{x} = \sqrt{\dfrac{\sum fm^{2}}{n} - \bar{x}^{2}} = \sqrt{\dfrac{193157.45}{30} - 79.5^{2}} = 10.88\)
- \(s_{x} = \sqrt{\dfrac{\sum fm^{2}}{n} - \bar{x}^{2}} = \sqrt{\dfrac{380945.3}{101} - 60.94^{2}} = 7.62\)
- \(s_{x} = \sqrt{\dfrac{\sum fm^{2}}{n} - \bar{x}^{2}} = \sqrt{\dfrac{440051.5}{86} - 70.66^{2}} = 11.14\)
Reuniéndolo
Ejercicio 2.8.7
A veinticinco estudiantes seleccionados al azar se les preguntó el número de películas que vieron la semana anterior. Los resultados son los siguientes:
| # de películas | Frecuencia |
|---|---|
| 0 | 5 |
| 1 | 9 |
| 2 | 6 |
| 3 | 4 |
| 4 | 1 |
- Encuentra la media muestral\(\bar{x}\).
- Encuentre la desviación estándar de la muestra aproximada,\(s\).
Contestar
- 1.48
- 1.12
Ejercicio 2.8.8
A cuarenta estudiantes seleccionados al azar se les preguntó el número de pares de zapatillas que poseían. Dejar que\(X =\) el número de pares de zapatillas de deporte poseídas. Los resultados son los siguientes:
| \(X\) | Frecuencia y |
|---|---|
| \ (X\) ">1 | 2 |
| \ (X\) ">2 | 5 |
| \ (X\) ">3 | 8 |
| \ (X\) ">4 | 12 |
| \ (X\) ">5 | 12 |
| \ (X\) ">6 | 0 |
| \ (X\) ">7 | 1 |
- Encuentra la media de la muestra\(\bar{x}\)
- Encuentra la desviación estándar de la muestra, s
- Construir un histograma de los datos.
- Completa las columnas del gráfico.
- Encuentra el primer cuartil.
- Encuentra la mediana.
- Encuentra el tercer cuartil.
- Construir una gráfica de caja de los datos.
- ¿Cuál por ciento de los estudiantes poseía al menos cinco parejas?
- Encuentra el percentil 40.
- Encuentra el percentil 90.
- Construir un gráfico de líneas de los datos
- Construir un stemplot de los datos
Ejercicio 2.8.9
A continuación se presentan los pesos publicados (en libras) de todos los integrantes del equipo de los 49ers de San Francisco de un año anterior.
177; 205; 210; 210; 232; 205; 185; 185; 178; 210; 206; 212; 184; 174; 185; 242; 188; 212; 215; 247; 241; 223; 220; 260; 245; 259; 278; 270; 280; 295; 275; 285; 290; 272; 273; 280; 285; 286; 200; 215; 185; 230; 250; 241; 190; 260; 250; 302; 265; 290; 276; 228; 265
- Organice los datos de menor a mayor valor.
- Encuentra la mediana.
- Encuentra el primer cuartil.
- Encuentra el tercer cuartil.
- Construir una gráfica de caja de los datos.
- El 50% medio de los pesos son de _______ a _______.
- Si nuestra población fuera toda futbolistas profesionales, ¿los datos anteriores serían una muestra de pesos o la población de pesos? ¿Por qué?
- Si nuestra población incluyera a cada miembro del equipo que alguna vez jugó para los 49ers de San Francisco, ¿los datos anteriores serían una muestra de pesos o la población de pesos? ¿Por qué?
- Supongamos que la población era de los 49ers de San Francisco. Encuentra:
- la media poblacional,\(\mu\).
- la desviación estándar poblacional,\(\sigma\).
- el peso que es dos desviaciones estándar por debajo de la media.
- Cuando Steve Young, mariscal de campo, jugaba al futbol, pesaba 205 libras. ¿Cuántas desviaciones estándar por encima o por debajo de la media era?
- Ese mismo año, el peso medio para los Dallas Cowboys fue de 240.08 libras con una desviación estándar de 44.38 libras. Emmit Smith pesaba en 209 libras. Con respecto a su equipo, ¿quién era más ligero, Smith o Young? ¿Cómo determinaste tu respuesta?
Contestar
- 174; 177; 178; 184; 185; 185; 185; 185; 188; 190; 200; 205; 205; 206; 210; 210; 210; 212; 212; 215; 215; 220; 223; 228; 230; 232; 241; 241; 242; 245; 247; 250; 250; 259; 260; 260; 265; 265; 270; 272; 273; 275; 276; 278; 280; 285; 285; 286; 290; 290; 295; 302
- 241
- 205.5
- 272.5

- 205.5, 272.5
- muestra
- población
-
- 236.34
- 37.50
- 161.34
- 0.84 std. dev. por debajo de la media
- Joven
Ejercicio 2.8.10
Un centenar de profesores asistieron a un seminario sobre resolución de problemas matemáticos. Se midieron las actitudes de una muestra representativa de 12 de los profesores antes y después del seminario. Un número positivo para el cambio de actitud indica que la actitud de un maestro hacia las matemáticas se volvió más positiva. Las 12 puntuaciones de cambio son las siguientes:
3; 8; —1; 2; 0; 5; —3; 1; —1; 6; 5; —2
- ¿Cuál es la media puntuación de cambio?
- ¿Cuál es la desviación estándar para esta población?
- ¿Cuál es la puntuación de cambio de mediana?
- Encuentra la puntuación de cambio que es 2.2 desviaciones estándar por debajo de la media.
Ejercicio 2.8.11
Refiérase a Figura determinar cuáles de los siguientes son verdaderos y cuáles son falsos. Explica tu solución a cada parte en oraciones completas.
<figure >

</figure>
- Las medianas para las tres gráficas son iguales.
- No podemos determinar si alguna de las medias para las tres gráficas es diferente.
- La desviación estándar para la gráfica b es mayor que la desviación estándar para la gráfica a.
- No podemos determinar si alguno de los terceros cuartiles para las tres gráficas es diferente.
Contestar
- Cierto
- Cierto
- Cierto
- Falso
Ejercicio 2.8.12
En un número reciente del IEEE Spectrum, se anunciaron 84 conferencias de ingeniería. Cuatro conferencias duraron dos días. Treinta y seis duraron tres días. Dieciocho duraron cuatro días. Diecinueve duraron cinco días. Cuatro duraron seis días. Uno duró siete días. Uno duró ocho días. Uno duró nueve días. Dejar X = la duración (en días) de una conferencia de ingeniería.
- Organizar los datos en un gráfico.
- Encuentra la mediana, el primer cuartil y el tercer cuartil.
- Encuentra el percentil 65.
- Encuentra el percentil 10.
- Construir una gráfica de caja de los datos.
- El 50% medio de las conferencias duran de _______ días a _______ días.
- Calcular la media muestral de días de conferencias de ingeniería.
- Calcular la desviación estándar muestral de días de conferencias de ingeniería.
- Encuentra el modo.
- Si estuvieras planeando una conferencia de ingeniería, ¿cuál elegirías como duración de la conferencia: media; mediana; o modo? Explica por qué hiciste esa elección.
- Da dos razones por las que piensas que de tres a cinco días parecen ser duraciones populares de conferencias de ingeniería.
Ejercicio 2.8.13
Una encuesta sobre la inscripción en 35 colegios comunitarios en los Estados Unidos arrojó las siguientes cifras:
6414; 1550; 2109; 9350; 21828; 4300; 5944; 5722; 2825; 2044; 5481; 5200; 5853; 2750; 10012; 6357; 27000; 9414; 7681; 3200; 17500; 9200; 7380; 18314; 6557; 13713; 17768; 7493; 2771; 2861; 1263; 7285; 165; 5080; 11622
- Organice los datos en un gráfico con cinco intervalos de igual ancho. Etiquetar las dos columnas “Inscripción” y “Frecuencia”.
- Construir un histograma de los datos.
- Si fueras a construir un nuevo colegio comunitario, ¿qué dato sería más valioso: el modo o la media?
- Calcular la media muestral.
- Calcular la desviación estándar de la muestra.
- Una escuela con una matrícula de 8000 sería ¿cuántas desviaciones estándar se alejarían de la media?
Contestar
-
Matrícula Frecuencia 1000-5000 10 5000-10000 16 10000-15000 3 15000-20000 3 20000-25000 1 25000-30000 2 - Consulta la solución del alumno.
- modo
- 8628.74
- 6943.88
- —0.09
Utilice la siguiente información para responder a los dos ejercicios siguientes. \(X =\)el número de días a la semana que 100 clientes utilizan una facilidad de ejercicio en particular.
| \(x\) | Frecuencia |
|---|---|
| \ (x\) ">0 | 3 |
| \ (x\) ">1 | 12 |
| \ (x\) ">2 | 33 |
| \ (x\) ">3 | 28 |
| \ (x\) ">4 | 11 |
| \ (x\) ">5 | 9 |
| \ (x\) ">6 | 4 |
Ejercicio 2.8.14
El percentil 80 es _____
- 5
- 80
- 3
- 4
Ejercicio 2.8.15
El número que es 1.5 desviaciones estándar ABAJO de la media es aproximadamente _____
- 0.7
- 4.8
- —2.8
- No se puede determinar
Contestar
a
Ejercicio 2.8.16
Supongamos que una editorial realizó una encuesta preguntando a los consumidores adultos el número de libros de bolsillo de ficción que habían comprado en el mes anterior. Los resultados se resumen en la Tabla.
| # de libros | Freq. | Rel. Freq. |
|---|---|---|
| 0 | 18 | |
| 1 | 24 | |
| 2 | 24 | |
| 3 | 22 | |
| 4 | 15 | |
| 5 | 10 | |
| 7 | 5 | |
| 9 | 1 |
- ¿Hay algún valor atípica en los datos? Use una prueba numérica apropiada que involucre el IQR para identificar valores atípicos, si los hubiera, y indique claramente su conclusión.
- Si un valor de datos se identifica como un valor atípico, ¿qué se debe hacer al respecto?
- ¿Hay algún valor de datos más allá de dos desviaciones estándar de la media? En algunas situaciones, los estadísticos pueden utilizar este criterio para identificar valores de datos que son inusuales, en comparación con los otros valores de datos. (Tenga en cuenta que este criterio es el más apropiado para usar para datos que tienen forma de montículo y simétricos, en lugar de para datos sesgados).
- ¿Las partes a y c de este problema dan la misma respuesta?
- Examine la forma de los datos. ¿Qué parte, a o c, de esta pregunta da un resultado más apropiado para estos datos?
- Con base en la forma de los datos cuál es la medida de centro más adecuada para estos datos: ¿media, mediana o modo?
Glosario
- Desviación estándar
- un número que es igual a la raíz cuadrada de la varianza y mide qué tan lejos están los valores de los datos de su media; notación: s para la desviación estándar de la muestra y σ para la desviación estándar de la población.
Colaboradores y Atribuciones
- Varianza
- media de las desviaciones cuadradas de la media, o el cuadrado de la desviación estándar; para un conjunto de datos, una desviación se puede representar como \(x\)—\(\bar{x}\) donde\(x\) es un valor de los datos y\(\bar{x}\) es la media de la muestra. La varianza muestral es igual a la suma de los cuadrados de las desviaciones dividida por la diferencia del tamaño de la muestra y uno.
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).


