6.3: Encontrar probabilidades para la distribución normal

Última actualización
Guardar como PDF

Page ID: 149808

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La Regla Empírica es solo una aproximación y sólo funciona para ciertos valores. ¿Y si quieres encontrar la probabilidad de valores x que no sean múltiplos enteros de la desviación estándar? La probabilidad es el área bajo la curva. Para encontrar áreas bajo la curva, necesitas cálculo. Antes de la tecnología, necesitaba convertir cada valor x a un número estandarizado, llamado puntaje z o valor z o simplemente z. La puntuación z es una medida de cuántas desviaciones estándar es un valor x de la media. Para convertir de un valor x normalmente distribuido a una puntuación z, utilice la siguiente fórmula.

Definición$\PageIndex{1}$: z-score

\[z=\dfrac{x-\mu}{\sigma} \label{z-score}\]

donde$\mu$ = media de la población del valor x y$\sigma$ = desviación estándar para la población del valor x

La puntuación z se distribuye normalmente, con una media de 0 y una desviación estándar de 1. Se le conoce como la curva normal estándar. Una vez que tenga la puntuación z, puede buscar la puntuación z en la tabla de distribución normal estándar.

Definición$\PageIndex{2}$: standard normal distribution

La distribución normal estándar, z, tiene una media de$\mu =0$ y una desviación estándar de$\sigma =1$.

Captura de pantalla (84) .png — Figura$\PageIndex{1}$: Curva normal estándar

Por suerte, en estos días la tecnología puede encontrar probabilidades para ti sin convertirte al zscore y mirar las probabilidades arriba en una tabla. Hay muchos programas disponibles que calcularán la probabilidad para una curva normal incluyendo Excel y el TI-83/84. También hay sitios en línea disponibles. Los siguientes ejemplos muestran cómo hacer el cálculo en el TI-83/84 y con R. El comando en el TI-83/84 se encuentra en el menú DISTR.C/84 y es normalcdf (. Luego escribe el límite inferior, el límite superior, la media, la desviación estándar en ese orden e incluyendo las comas. El comando en R para encontrar el área a la izquierda es pnorm (valor z o valor x, media, desviación estándar).

Ejemplo$\PageIndex{1}$ general normal distribution

La duración de un embarazo humano normalmente se distribuye con una media de 272 días con una desviación estándar de 9 días (Bhat & Kushtagi, 2006).

Anote la variable aleatoria.
Encuentra la probabilidad de un embarazo que dure más de 280 días.
Encuentra la probabilidad de que un embarazo dure menos de 250 días.
Encuentra la probabilidad de que un embarazo dure entre 265 y 280 días.
Encuentra la duración del embarazo que el 10% de todos los embarazos duran menos de.
Supongamos que conoces a una mujer que dice que estuvo embarazada por menos de 250 días. ¿Sería esto inusual y qué pensarías?

Solución

a. x = duración de un embarazo humano

b. Primero traduzca la declaración en una declaración matemática.

P (x>280)

Ahora, dibuja un cuadro. Recuerda que el centro de esta curva normal es 272.

Captura de pantalla (85) .png — Figura para el Ejemplo$\PageIndex{1}$ b

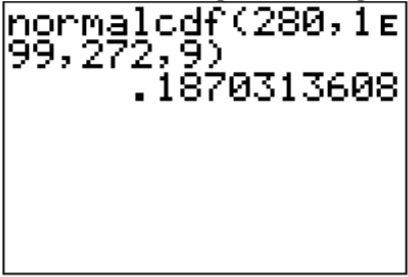
Para encontrar la probabilidad en el TI-83/84, mirando la imagen te das cuenta que el límite inferior es 280. El límite superior es infinito. La calculadora no tiene infinito en ella, así que necesitas poner un número realmente grande. A algunas personas les gusta poner en 1000, pero si estás trabajando con números que son mayores a 1000, entonces tendrías que recordar cambiar el límite superior. El número más seguro para usar es$1 \times 10^{99}$, que pones en la calculadora como 1E99 (donde E es el botón EE en la calculadora). El comando se ve así:

$\text{normalcdf}(280,1 E 99,272,9)$

Captura de pantalla (86) .png — Figura$\PageIndex{3}$: Salida TI-83/84 para el Ejemplo$\PageIndex{1}$ b

Para encontrar la probabilidad en R, R siempre da la probabilidad a la izquierda del valor. El área total bajo la curva es 1, así que si quieres el área a la derecha, entonces encuentras el área a la izquierda y restas de 1. El comando se ve así:

$1-\text { pnom }(280,272,9)$

Por lo tanto,$P(x>280) \approx 0.187$

Así, 18.7% de todos los embarazos duran más de 280 días. Esto no es inusual ya que la probabilidad es mayor al 5%.

c. Primero traduzca la declaración en una declaración matemática.

P (x<250)

Ahora, dibuja un cuadro. Recuerda que el centro de esta curva normal es 272.

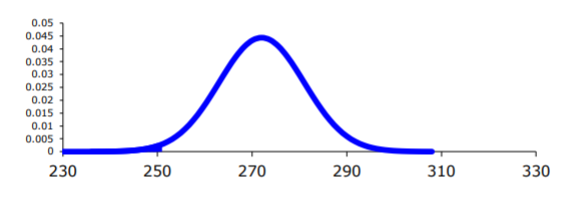Captura de pantalla (87) .png — Figura para el Ejemplo$\PageIndex{1}$ c

Para encontrar la probabilidad en el TI-83/84, mirando la imagen, aunque es difícil de ver en este caso, el límite inferior es infinito negativo. Nuevamente, la calculadora no tiene esto en ella, ponga un número realmente pequeño, como$-1 \times 10^{99}=-1 E 99$ en la calculadora.

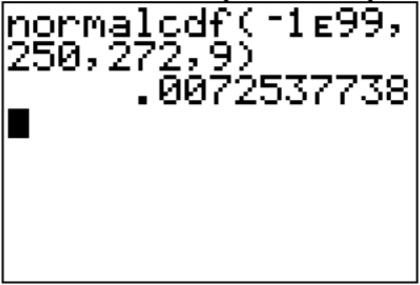Captura de pantalla (88) .png — Figura$\PageIndex{5}$: Salida TI-83/84 para el Ejemplo$\PageIndex{1}$ c

$P(x<250)=\text { normalcdf }(-1 E 99,250,272,9)=0.0073$

Para encontrar la probabilidad en R, R siempre da la probabilidad a la izquierda del valor. Mirando la figura, puedes ver que el área que deseas está a la izquierda. El comando se ve así:

$P(x<250)=\text { pnorm }(250,272,9)=0.0073$

Así 0.73% de todos los embarazos duran menos de 250 días. Esto es inusual ya que la probabilidad es inferior al 5%.

d. Primero traduzca la declaración en una declaración matemática.

P (265<x<280)

Ahora, dibuja un cuadro. Recuerda que el centro de esta curva normal es 272.

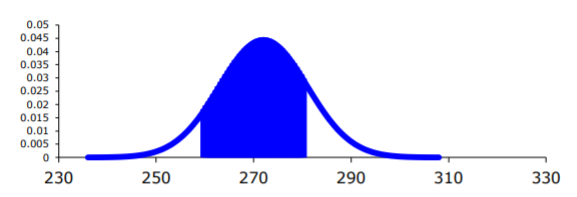Captura de pantalla (89) .png — Figura para el Ejemplo$\PageIndex{1}$ d

En este caso, el límite inferior es 265 y el límite superior es 280.

Uso de la calculadora

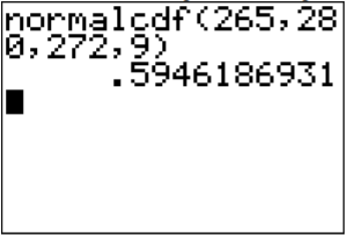Captura de pantalla (90) .png — Figura$\PageIndex{7}$: Salida TI-83/84 para el Ejemplo$\PageIndex{1}$ d

$P(265<x<280)=\text { normalcdf }(265,280,272,9)=0.595$

Para usar R, hay que recordar que R te da el área a la izquierda. Así$P(x<280)=\text { pnom }(280,272,9)$ es el área a la izquierda de 280 y$P(x<265)=\text { pnom }(265,272,9)$ es el área a la izquierda de 265. Entonces el área está entre los dos sería el más grande menos el más pequeño. Entonces,$P(265<x<280)=\text { pnorm }(280,272,9)-\text { pnorm }(265,272,9)=0.595$. Así, 59.5% de todos los embarazos duran entre 265 y 280 días.

e. Este problema es pedirle encontrar un valor x a partir de una probabilidad. Se quiere encontrar el valor x que tiene el 10% de la duración de los embarazos a la izquierda del mismo. En el TI-83/84, el comando se encuentra en el menú DISTR.C/y se llama InvNorm (. El comando InvNorm (necesita el área a la izquierda. En este caso, esa es la zona que se le da. Para el comando en la calculadora, una vez que tienes InvNorm (en la pantalla principal se escribe la probabilidad a la izquierda, media, desviación estándar, en ese orden con las comas.

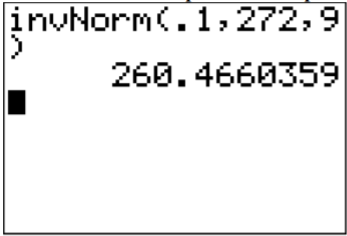Captura de pantalla (91) .png — Figura$\PageIndex{8}$: Salida TI-83/84 para el Ejemplo$\PageIndex{1}$ e

En R, el comando es qnorm (área a la izquierda, media, desviación estándar). Para este ejemplo eso sería qnorm (0.1, 272, 9)

Así, el 10% de todos los embarazos duran menos de aproximadamente 260 días.

f. de la parte (c) encontraste que la probabilidad de que un embarazo dure menos de 250 días es de 0.73%. Dado que esto es menos del 5%, es muy inusual. Se pensaría que o la mujer tuvo un bebé prematuro, o que puede estar equivocada acerca de cuándo realmente quedó embarazada.

Ejemplo$\PageIndex{2}$ general normal distribution

La puntuación media en matemáticas SAT en 2012 fue 514 con una desviación estándar de 117 (“Perfil total del grupo”, 2012). Supongamos que el puntaje SAT de matemáticas se distribuye normalmente.

Anote la variable aleatoria.
Encuentra la probabilidad de que una persona tenga un puntaje SAT de matemáticas superior a 700.
Encuentra la probabilidad de que una persona tenga un puntaje SAT de matemáticas inferior a 400.
Encuentra la probabilidad de que una persona tenga un puntaje SAT de matemáticas entre un 500 y un 650.
Encuentra el puntaje SAT de matemáticas que representa el 1% superior de todas las puntuaciones.

Solución

a. x = puntaje SAT de matemáticas

b. Primero traduzca la declaración en una declaración matemática.

P (x>700)

Ahora, dibuja un cuadro. Recuerda que el centro de esta curva normal es 514.

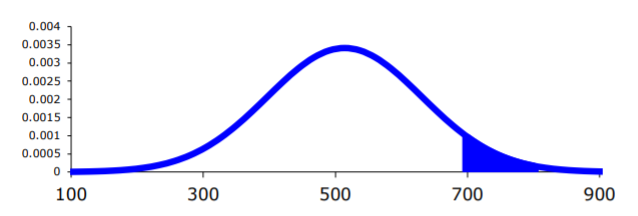Captura de pantalla (92) .png — Figura para el Ejemplo$\PageIndex{2}$ b

En TI-83/84:$P(x>700)=\text { normalcdf }(700,1 E 99,514,117) \approx 0.056$

En R:$P(x>700)=1-\text { pnorm }(700,514,117) \approx 0.056$

Hay un 5.6% de probabilidad de que una persona tenga una puntuación superior a 700 en la prueba SAT de matemáticas. Esto no es inusual.

c. Primero traduzca la declaración en una declaración matemática.

P (x<400)

Ahora, dibuja un cuadro. Recuerda que el centro de esta curva normal es 514.

Captura de pantalla (93) .png — Figura para el Ejemplo$\PageIndex{2}$ c

En TI-83/84:$P(x<400)=\text { normalcdf }(-1 E 99,400,514,117) \approx 0.165$

En R:$P(x<400)=\operatorname{pnorm}(400,514,117) \approx 0.165$

Entonces, hay un 16.5% de probabilidad de que una persona tenga una puntuación inferior a 400 en la parte matemática del SAT.

d. Primero traduzca la declaración en una declaración matemática.

P (500<x<650)

Ahora, dibuja un cuadro. Recuerda que el centro de esta curva normal es 514.

Captura de pantalla (94) .png — Figura para el Ejemplo$\PageIndex{2}$ d

En TI-83/84:$P(500<x<650)=\text { normalcdf }(500,650,514,117) \approx 0.425$

En R:$P(500<x<650)=\text { pnorm }(650,514,117)-\text { pnorm }(500,514,117) \approx 0.425$

Entonces, hay un 42.5% de probabilidad de que una persona tenga un puntaje SAT matemático entre 500 y 650.

e. Este problema es pedirle encontrar un valor x a partir de una probabilidad. Se quiere encontrar el valor x que tiene 1% de las puntuaciones del SAT de matemáticas a la derecha del mismo. Recuerda, la calculadora y R siempre necesitan el área a la izquierda, necesitas encontrar el área a la izquierda por 1 - 0.01 = 0.99.

En TI-83/84:$\text{invNorm}(.99,514,117) \approx 786$

En R:$\text{qnorm}(.99,514,117) \approx 786$

Entonces, el 1% de todas las personas que tomaron el SAT anotaron más de 786 puntos en el SAT de matemáticas.

Testo

Ejercicio$\PageIndex{1}$

Encuentra cada una de las probabilidades, donde z es una puntuación z de la distribución normal estándar con media de$\mu =0$ y desviación estándar$\sigma =1$. Asegúrate de dibujar un dibujo para cada problema.
1. P (z<2.36)
2. P (z>0.67)
3. P (0<z<2.11)
4. P (-2.78<z<1.97)
Encuentra la puntuación z correspondiente al área dada. Recuerde, z se distribuye como la distribución normal estándar con media$\mu =0$ y desviación estándar$\sigma =1$.
1. El área a la izquierda de z es del 15%.
2. El área a la derecha de z es 65%.
3. El área a la izquierda de z es del 10%.
4. El área a la derecha de z es del 5%.
5. El área entre -z y z es del 95%. (Pista dibujar una imagen y averiguar el área a la izquierda de la -z.)
6. El área entre -z y z es del 99%.
Si una variable aleatoria que se distribuye normalmente tiene una media de 25 y una desviación estándar de 3, convierta el valor dado a una puntuación z.
1. x = 23
2. x = 33
3. x = 19
4. x = 45
Según el Proyecto MONICA de la OMS la presión arterial media para las personas en China es de 128 mmHg con una desviación estándar de 23 mmHg (Kuulasmaa, Hense & Tolonen, 1998). Supongamos que la presión arterial se distribuye normalmente.
1. Anote la variable aleatoria.
2. Encuentra la probabilidad de que una persona en China tenga presión arterial de 135 mmHg o más.
3. Encuentra la probabilidad de que una persona en China tenga presión arterial de 141 mmHg o menos.
4. Encuentra la probabilidad de que una persona en China tenga presión arterial entre 120 y 125 mmHg.
5. ¿Es inusual que una persona en China tenga una presión arterial de 135 mmHg? ¿Por qué o por qué no?
6. ¿Qué presión arterial tiene menos de 90% de todas las personas en China?
El tamaño de los peces es muy importante para la pesca comercial. Un estudio realizado en 2012 encontró que la longitud del bacalao atlántico capturado en redes en Karlskrona tenía una media de 49.9 cm y una desviación estándar de 3.74 cm (Ovejgard, Berndt & Lunneryd, 2012). Supongamos que la longitud de los peces se distribuye normalmente.
1. Anote la variable aleatoria.
2. Encuentra la probabilidad de que un bacalao atlántico tenga una longitud menor a 52 cm.
3. Encuentra la probabilidad de que un bacalao atlántico tenga una longitud superior a 74 cm.
4. Encuentra la probabilidad de que un bacalao atlántico tenga una longitud entre 40.5 y 57.5 cm.
5. Si encontraste que un bacalao atlántico tiene una longitud superior a 74 cm, ¿qué podrías concluir?
6. ¿Cuál es la longitud del 15% de todo el bacalao atlántico más largos que
Los niveles medios de colesterol de las mujeres de 45 a 59 años en Ghana, Nigeria y Seychelles son de 5.1 mmol/l y la desviación estándar es de 1.0 mmol/l (Lawes, Hoorn, Law & Rodgers, 2004). Supongamos que los niveles de colesterol se distribuyen normalmente.
1. Anote la variable aleatoria.
2. Encuentra la probabilidad de que una mujer de 45-59 años en Ghana, Nigeria o Seychelles tenga un nivel de colesterol superior a 6.2 mmol/l (considerado un nivel alto).
3. Encuentra la probabilidad de que una mujer de 45-59 años en Ghana, Nigeria o Seychelles tenga un nivel de colesterol por debajo de 5.2 mmol/l (considerado un nivel normal).
4. Encuentra la probabilidad de que una mujer de 45-59 años en Ghana, Nigeria o Seychelles tenga un nivel de colesterol entre 5.2 y 6.2 mmol/l (considerado como límite alto).
5. Si encontraste a una mujer de 45 a 59 años en Ghana, Nigeria o Seychelles con un nivel de colesterol superior a 6.2 mmol/l, ¿qué podrías concluir?
6. ¿Qué valor tiene el 5% de todas las mujeres de 45 a 59 años en Ghana, Nigeria o Seychelles tienen un nivel de colesterol inferior a?
En Estados Unidos, los machos de entre 40 y 49 años comen en promedio 103.1 g de grasa todos los días con una desviación estándar de 4.32 g (“Qué comemos”, 2012). Supongamos que la cantidad de grasa que come una persona normalmente se distribuye.
1. Anote la variable aleatoria.
2. Encuentra la probabilidad de que un hombre de 40 a 49 años en Estados Unidos coma más de 110 g de grasa todos los días.
3. Encuentra la probabilidad de que un hombre de 40 a 49 años en Estados Unidos coma menos de 93 g de grasa todos los días.
4. Encuentra la probabilidad de que un hombre de 40 a 49 años en Estados Unidos coma menos de 65 g de grasa todos los días.
5. Si encontraras a un hombre de 40 a 49 años en EU que dice que come menos de 65 g de grasa todos los días, ¿le creerías? ¿Por qué o por qué no?
6. ¿Qué nivel diario de grasa come más de 5% de todos los hombres de 40 a 49 años en Estados Unidos?
Un lavavajillas tiene una vida media de 12 años con una desviación estándar estimada de 1.25 años (“Esperanza de vida del aparato”, 2013). Supongamos que la vida útil de un lavavajillas se distribuye normalmente.
1. Anote la variable aleatoria.
2. Encuentra la probabilidad de que un lavavajillas dure más de 15 años.
3. Encuentra la probabilidad de que un lavavajillas dure menos de 6 años.
4. Encuentra la probabilidad de que un lavavajillas dure entre 8 y 10 años.
5. Si encontraras un lavavajillas que durara menos de 6 años, ¿pensarías que tienes algún problema con el proceso de fabricación? ¿Por qué o por qué no?
6. Un fabricante de lavavajillas solo quiere sustituir de forma gratuita el 5% de todos los lavavajillas. ¿Cuánto tiempo debe hacer el fabricante el periodo de garantía?
El salario inicial medio para las enfermeras es de $67,694 a nivel nacional (“Staff nurse -”, 2013). La desviación estándar es de aproximadamente $10,333. Supongamos que el salario inicial se distribuye normalmente.
1. Anote la variable aleatoria.
2. Encuentra la probabilidad de que una enfermera titular gane más de $80,000.
3. Encuentra la probabilidad de que una enfermera titular gane menos de $60,000.
4. Encuentra la probabilidad de que una enfermera titular gane entre $55,000 y $72,000.
5. Si una enfermera ganara menos de 50.000 dólares, ¿pensaría que la enfermera estaba mal pagada? ¿Por qué o por qué no?
6. ¿Qué salario gana más el 30% de todas las enfermeras?
La precipitación media anual en Sydney, Australia, es de aproximadamente 137 mm y la desviación estándar es de aproximadamente 69 mm (“Máximo anual de”, 2013). Supongamos que las precipitaciones se distribuyen normalmente.
1. Anote la variable aleatoria.
2. Encuentra la probabilidad de que la precipitación anual sea inferior a 100 mm.
3. Encuentra la probabilidad de que la precipitación anual sea superior a 240 mm.
4. Encuentra la probabilidad de que la precipitación anual esté entre 140 y 250 mm.
5. Si un año tiene una precipitación inferior a 100mm, ¿significa eso que es un año inusualmente seco? ¿Por qué o por qué no?
6. ¿Qué cantidad de precipitaciones son más del 90% de todas las lluvias anuales?

Contestar

1. a.$P(z<2.36)=0.9909$, b.$P(z>0.67)=0.2514$, c.$P(0<z<2.11)=0.4826$, d.$P(-2.78<z<1.97)=0.9729$

3. a. -0.6667, b. -2.6667, c. -2, d. 6.6667

5. a. Ver soluciones, b.$P(x<52 \mathrm{cm})=0.7128$, c.$P(x>74 \mathrm{cm})=5.852 \times 10^{-11}$, d.$P(40.5 \mathrm{cm}<x<57.5 \mathrm{cm})=0.9729$, e. Ver soluciones, f. 53.8 cm

7. a. Ver soluciones, b.$P(x>110 \mathrm{g})=0.0551$ c.$P(x<93 \mathrm{g})=0.0097$, d.$P(x<65 \mathrm{g}) \approx 0$ o$5.57 \times 10^{-19}$, e. Ver soluciones, f. 110.2 g

9. a. Ver soluciones, b.$P(x>\$ 80,000)=0.1168$, c.$P(x>\$ 80,000)=0.2283$, d.$P(\$ 55,000<x<\$ 72,000)=0.5519$, e. Ver soluciones, f. $73.112