7: Análisis de Datos Cuantitativos Bivariados
- Page ID
- 150379
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Durante los últimos tres capítulos has estado aprendiendo a hacer inferencias para datos univariados. Para cada pregunta de investigación que se pudiera hacer, solo se necesitaba una variable aleatoria para la respuesta. Esa variable aleatoria podría ser categórica o cuantitativa. En algunos casos, la misma variable aleatoria podría ser muestreada y comparada para dos poblaciones diferentes, pero eso aún la convierte en datos univariados. En este capítulo, exploraremos datos cuantitativos bivariados. Esto significa que por cada unidad de nuestra muestra se determinarán dos variables cuantitativas. El propósito de recolectar dos variables cuantitativas es determinar si existe una relación entre ellas.
La última vez que se discutió el análisis de dos variables cuantitativas fue en el Capítulo 4 cuando aprendió a hacer un diagrama de dispersión y encontrar la correlación. En su momento, se enfatizó que aunque exista una correlación, ese hecho por sí solo es insuficiente para probar la causalidad. Hay una variedad de posibles explicaciones que podrían proporcionarse para una correlación observada. Estos se enumeraron en el Capítulo 4 y se proporcionaron nuevamente aquí.
- Cambiar la variable x provocará un cambio en la variable y
- Cambiar la variable y provocará un cambio en la variable x
- Puede existir un bucle de retroalimentación en el que un cambio en la variable x conduzca a un cambio en la variable y que conduzca a otro cambio en la variable x, etc.
- Los cambios en ambas variables están determinados por una tercera variable
- Los cambios en ambas variables son coincidentes.
- La correlación es el resultado de valores atípicos, sin los cuales no habría correlación significativa.
- La correlación es el resultado de variables confusas.
La causalidad es más fácil de probar con un experimento manipulador que con un experimento observacional. En un experimento manipulador, el investigador asignará aleatoriamente sujetos a diferentes grupos, disminuyendo así cualquier posible efecto de variables confusas. En experimentos observacionales, las variables de confusión no pueden distribuirse equitativamente a lo largo de la población estudiada. Los experimentos manipuladores no siempre se pueden hacer por razones éticas. Por ejemplo, la tierra se encuentra actualmente en un experimento observacional en el que la variable explicativa es la cantidad de combustibles fósiles que se están convirtiendo en dióxido de carbono y la variable de respuesta es la temperatura global media. Se habría considerado poco ético si un científico hubiera propuesto en el siglo XIX que deberíamos quemar tantos combustibles fósiles como fuera posible para ver cómo afecta la temperatura global. De igual manera, los experimentos que obligarían a alguien a fumar, enviar mensajes de texto mientras conducía, o realizar otras acciones peligrosas no se considerarían éticos y por lo tanto se deben buscar correlaciones utilizando experimentos observacionales.
Existen varias razones por las que es apropiado recolectar y analizar datos bivariados. Una de esas razones es que la variable dependiente o respuesta es de mayor interés pero la variable independiente o explicativa es más fácil de medir. Por lo tanto, si existe una fuerte relación entre la variable explicativa y la de respuesta, esa relación se puede utilizar para calcular la variable de respuesta utilizando datos de la variable explicativa. Por ejemplo, a un médico realmente le gustaría saber el grado en que se bloquean las arterias coronarias de un paciente, pero la presión arterial es más fácil de obtener datos. Por lo tanto, dado que existe una fuerte relación entre la presión arterial y el grado en que se bloquean las arterias, entonces la presión arterial puede ser utilizada como herramienta predictiva.
Otra razón para recopilar y analizar datos bivariados es establecer normas para una población. Como ejemplo, los infantes son pesados y medidos al nacer y debe existir una correlación entre su peso y longitud (¿talla?). Un bebé que esté sustancialmente por debajo del peso en comparación con los bebés de la misma longitud plantearía preocupaciones para el médico.
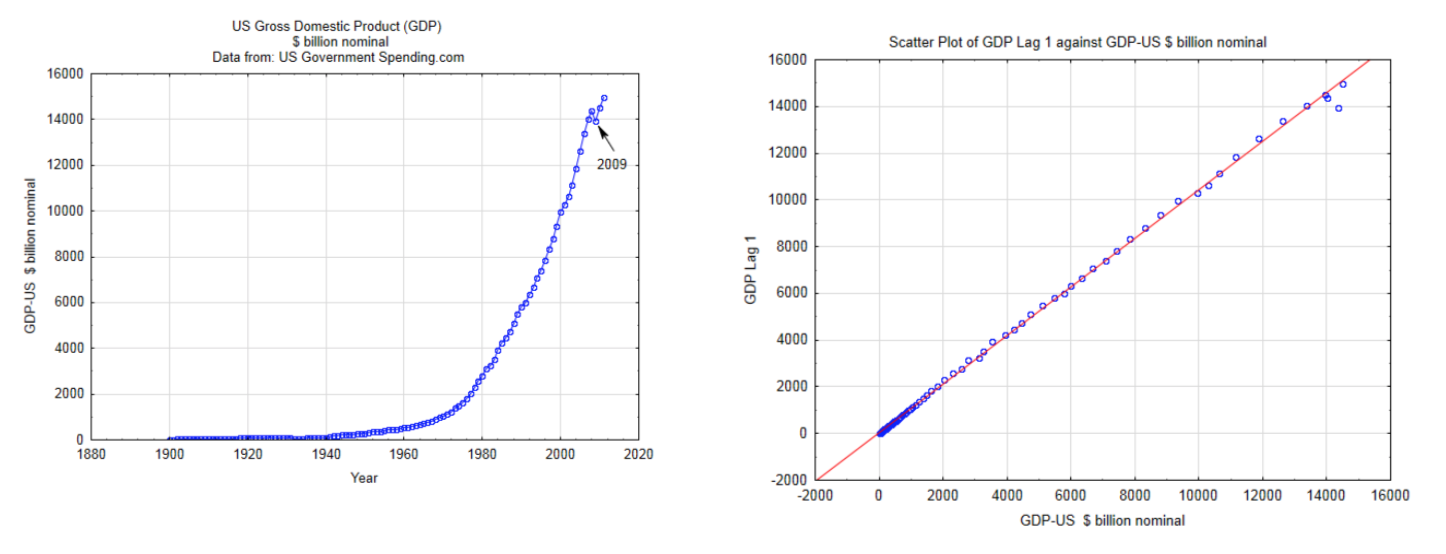
Para utilizar los métodos descritos en este capítulo, los datos deben ser independientes, cuantitativos, continuos y tener una distribución normal bivariada. El uso de datos cuantitativos discretos excede los alcances de este capítulo. Independencia significa que la magnitud de un valor de datos no afecta la magnitud de otro valor de datos. Esto a menudo se viola cuando se utilizan datos de series temporales. Por ejemplo, los datos anuales del PIB (producto interno bruto) no deben utilizarse como una de las variables aleatorias para el análisis de datos bivariados debido a que el tamaño de la economía en un año tiene una tremenda influencia en el tamaño de la misma al año siguiente. Esto se muestra en las dos gráficas a continuación. La gráfica de la izquierda es una gráfica de series temporales del PIB real para Estados Unidos. La gráfica de la derecha es una gráfica de dispersión que utiliza el PIB para EU como la variable x y el PIB para EU un año después (lag 1) para el valor y. El hecho de que estos puntos estén en una línea tan recta indica que los datos no son independientes. En consecuencia, estos datos no deben ser utilizados en el tipo de análisis que se discutirán en este capítulo.
Una distribución normal bivariada es aquella en la que los valores y se distribuyen normalmente para cada valor x y los valores x se distribuyen normalmente para cada valor y. Si esto pudiera ser graficado en tres dimensiones, la superficie se vería como una montaña con un pico redondeado.
Volveremos ahora al ejemplo del capítulo 4 en el que se exploró la relación entre la brecha de riqueza, medida por el Coeficiente de Gini, y la pobreza. La vida puede ser más difícil para quienes se encuentran en la pobreza y ciertamente la influencia que pueden tener en el país es mucho más limitada que aquellos que son ricos. Dado que las personas en pobreza deben canalizar sus energías hacia la supervivencia, tienen menos tiempo y energía para dedicarse a cosas que beneficiarían a la humanidad en su conjunto. Por lo tanto, es de interés de todas las personas encontrar la manera de reducir la pobreza y con ello aumentar el número de personas que puedan ayudar al mundo a mejorar.
Hay muchas variables posibles que podrían contribuir a la pobreza. A continuación se muestra una lista parcial. No todas son variables cuantitativas y algunas pueden ser difíciles de medir, pero aún pueden tener un impacto en los niveles de pobreza
- Educación
- Nivel de ingresos de los padres
- Nivel de ingresos de la comunidad
- Disponibilidad de empleo
- Salud Mental
- Conocimiento
- Motivación y determinación
- Discapacidades físicas o enfermedades
- Brecha de riqueza
- Raza/etnidad/estatus migratorio/género
- Porcentaje de la población que está ocupada
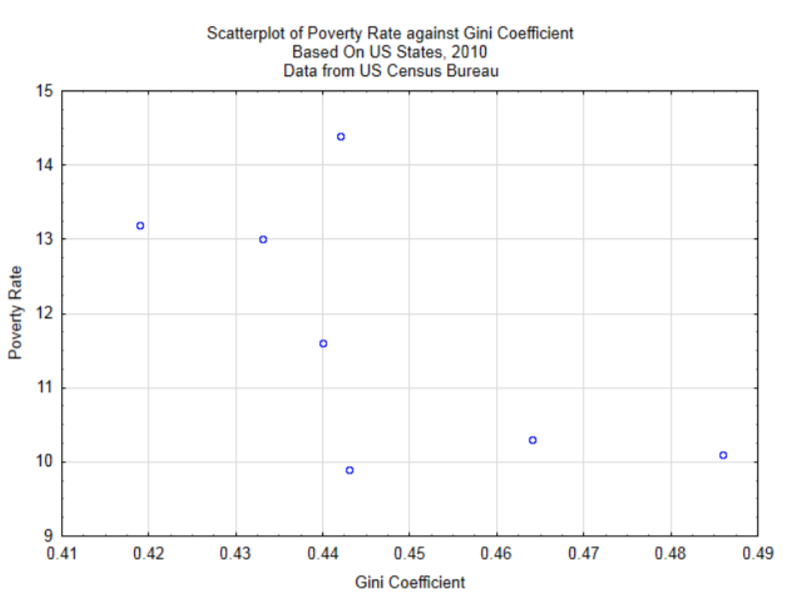
En el Capítulo 4, solo se exploró la relación entre la brecha de riqueza y el nivel de pobreza. Se recopilaron datos de siete estados para determinar si existe correlación entre estas dos variables. El diagrama de dispersión se reproduce a continuación. La correlación es -0.65.
Como recordatorio, la correlación es un número entre -1 y 1. La correlación poblacional se representa con la letra griega\(\rho\), mientras que el coeficiente de correlación muestral se representa con la letra\(r\). Una correlación de 0 indica que no hay correlación, mientras que una correlación de 1 o -1 indica una correlación perfecta. La cuestión es si la población subyacente tiene una relación lineal significativa. La evidencia de esto proviene de la muestra. Las hipótesis que normalmente se prueban son:
\(H_0: \rho = 0\)
\(H_1: \rho \ne 0\)
Esta es una prueba de dos colas para una hipótesis alternativa no direccional. Un resultado significativo indica únicamente que la correlación no es 0, no indica la dirección de la correlación.
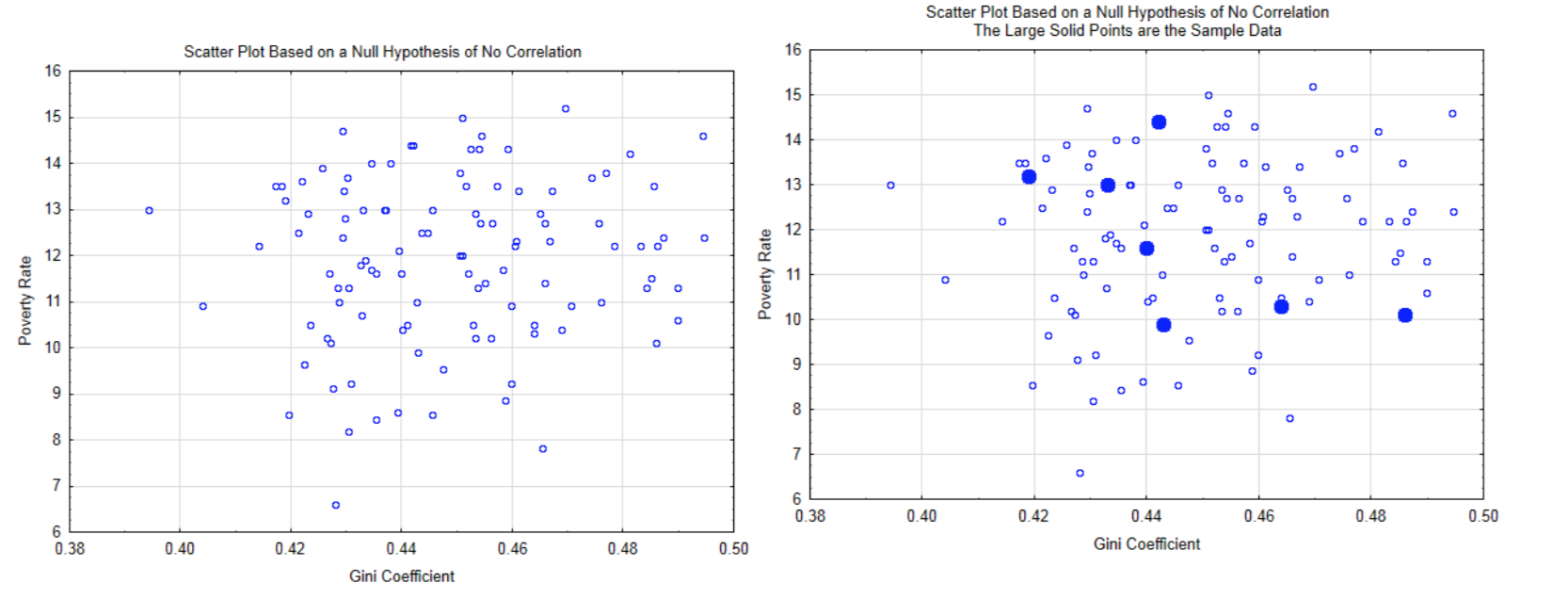
La lógica detrás de esta prueba de hipótesis se basa en el supuesto de que la hipótesis nula es verdadera, lo que significa que no hay correlación en la población. Un ejemplo se muestra en la gráfica de dispersión de la izquierda. A partir de esta distribución, se calcula la probabilidad de obtener los datos de muestra (mostrados en círculos sólidos en la gráfica de la derecha), o datos más extremos (formando una línea más recta).
La prueba utilizada para determinar si la correlación es significativa es una prueba t. La fórmula es:
\[t = \dfrac{r\sqrt{n - 2}}{\sqrt{1 - r^2}}.\]
Hay n - 2 grados de libertad.
Esto se puede demostrar con el ejemplo de los coeficientes de Gini y las tasas de pobreza previstos en el Capítulo 4 y utilizando un nivel de significancia de 0.05. La correlación es -0.650. El tamaño de la muestra es de 7, por lo que hay 5 grados de libertad. Después de sustituir en el estadístico de prueba,\(t = \dfrac{-0.650 \sqrt{7 - 2}}{\sqrt{1 - (-0.650)^2}}\), el valor del estadístico de prueba es -1.91. Basado en la tabla t con 5 grados de libertad, el valor p bilateral es mayor que 0.10 (0.1140 real). En consecuencia, no existe una correlación significativa entre el coeficiente de Gini y las tasas de pobreza.
Otra variable explicativa que se puede investigar por su correlación con las tasas de pobreza es la relación empleo-población (por ciento). Este es el porcentaje de la población que se emplea al menos una hora en el mes
. 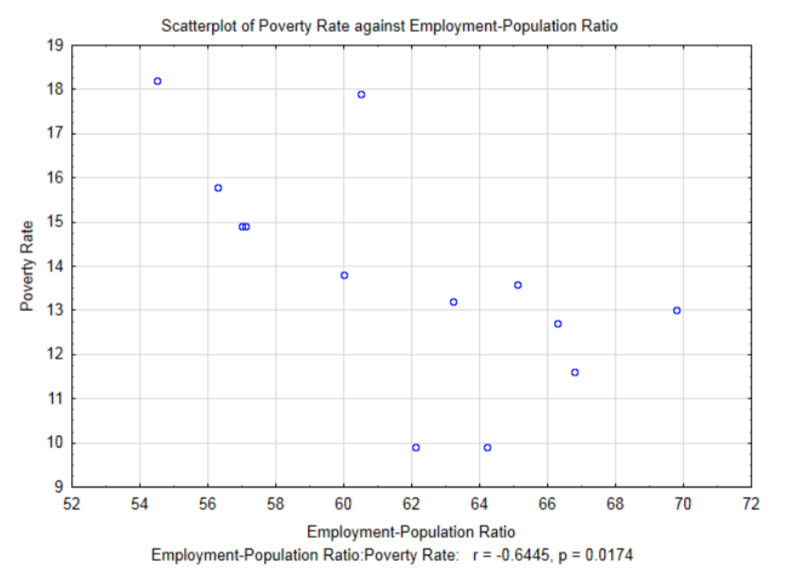
La correlación para estos datos es -0.6445,\(t\) = -2.80 y\(p\) = 0.0174. Observe en el nivel 0.05 de significancia, esta correlación es significativa. Antes de explorar el significado de una correlación significativa, compare los resultados de la correlación entre el Coeficiente de Gini y la tasa de pobreza que fue de -0.650 y los resultados de la correlación entre la Relación Empleo-Población y las tasas de pobreza que es -0.6445. La correlación anterior no fue significativa mientras que la posterior fue significativa a pesar de que es menor que la anterior. Este es un buen ejemplo de por qué el conocimiento de un coeficiente de correlación no es suficiente información para determinar si la correlación es significativa. El otro factor que influye en la determinación de significancia es el tamaño de la muestra. Los datos de relación empleo-población/tasas de pobreza se determinaron a partir de un tamaño muestral mayor (13 frente a 7). El tamaño de la muestra juega un papel importante en la determinación de si se apoya la alternativa. Con muestras muy grandes, se puede demostrar que las correlaciones de muestra muy pequeñas son significativas. La cuestión es si significativo corresponde con importante.
El efecto del tamaño de la muestra sobre las posibles correlaciones se muestra en las cuatro distribuciones siguientes. Estas distribuciones se crearon partiendo de una población que tuvo una correlación de\(\rho = 0.000\) .10,000 muestras de tamaño 5,15,35, y se extrajeron 300 de esta población, con reemplazo.
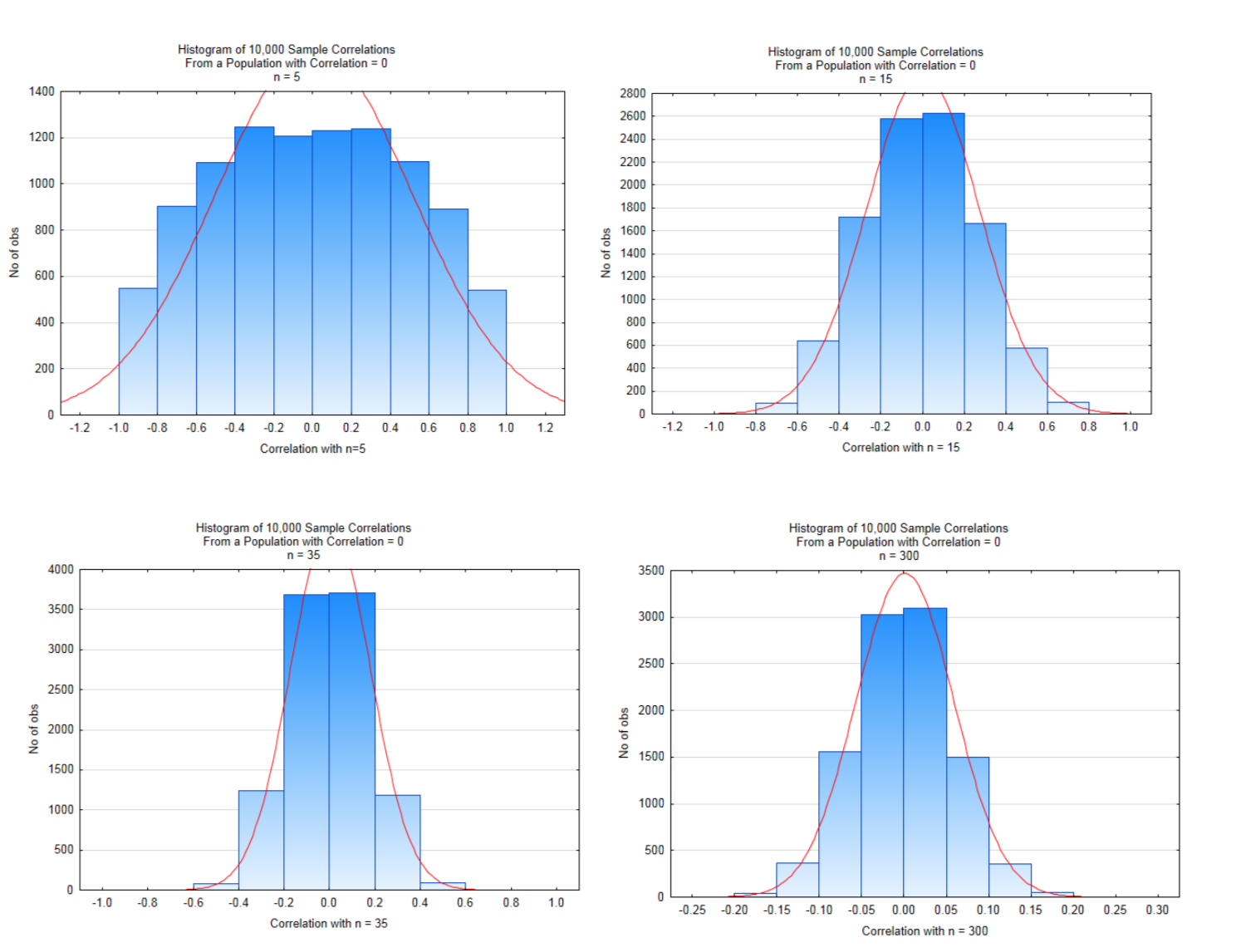
Observe cuidadosamente las escalas del eje x y las alturas de las barras. Los valores cercanos a la mitad de las gráficas son valores probables, mientras que los valores en el extremo izquierdo y derecho de la gráfica son valores poco probables que, al probar una hipótesis, posiblemente conducirían a una conclusión significativa. Con tamaños de muestra pequeños, la magnitud de la correlación debe ser muy grande para concluir que existe correlación significativa. A medida que aumenta el tamaño de la muestra, la magnitud de la correlación puede ser mucho menor para concluir que hay correlación significativa. Los valores críticos para cada uno de estos se muestran en la tabla siguiente y se basan en una prueba de dos colas con un nivel de significancia de 5%.
| n | 5 | 15 | 35 | 300 |
|---|---|---|---|---|
| t | 2.776 | 2.145 | 2.032 | 1.968 |
| |r| | 0.848 | 0.511 | 0.334 | 0.113 |
En el histograma de la parte inferior derecha en el que el tamaño muestral era de 300, una correlación que supera 0.113 conduciría a una conclusión de correlación significativa, sin embargo, existe la cuestión de si una correlación tan pequeña es muy significativa, aunque sea significativa. Podría ser significativo o puede que no. El investigador deberá determinar eso para cada situación.
Volviendo al análisis de los coeficientes de Gini y las tasas de pobreza, ya que no hubo una correlación significativa entre estas dos variables, entonces no tiene sentido tratar de utilizar los Coeficientes de Gini para estimar las tasas de pobreza o enfocarse en los cambios en la brecha de riqueza como una forma de mejorar la tasa de pobreza. Podría haber otras razones para querer cambiar la brecha de riqueza, pero su impacto en las tasas de pobreza no parece ser una de las razones. Por otro lado, debido a que existe una correlación significativa entre la Relación Empleo-Población y las tasas de pobreza, entonces es razonable utilizar la relación entre ellas como modelo para estimar las tasas de pobreza para Ratios Empleo-Población específicos. Si se puede determinar que esta relación es causal, entonces justifica mejorar la relación empleo-población para ayudar a reducir las tasas de pobreza. Es decir, la gente necesita empleos para salir de la pobreza.
Dado que el Coeficiente de Correlación Momento del Producto de Pearson mide la fuerza de la relación lineal entre las dos variables, entonces es razonable encontrar la ecuación de la línea que mejor se ajuste a los datos. Esta línea se llama la línea de regresión de mínimos cuadrados o la línea de mejor ajuste. Se ha agregado una línea de regresión a la gráfica para la Relación Empleo-Población y Tasas de Pobreza. Observe que hay una pendiente negativa a la línea. Esto corresponde al signo del coeficiente de correlación.
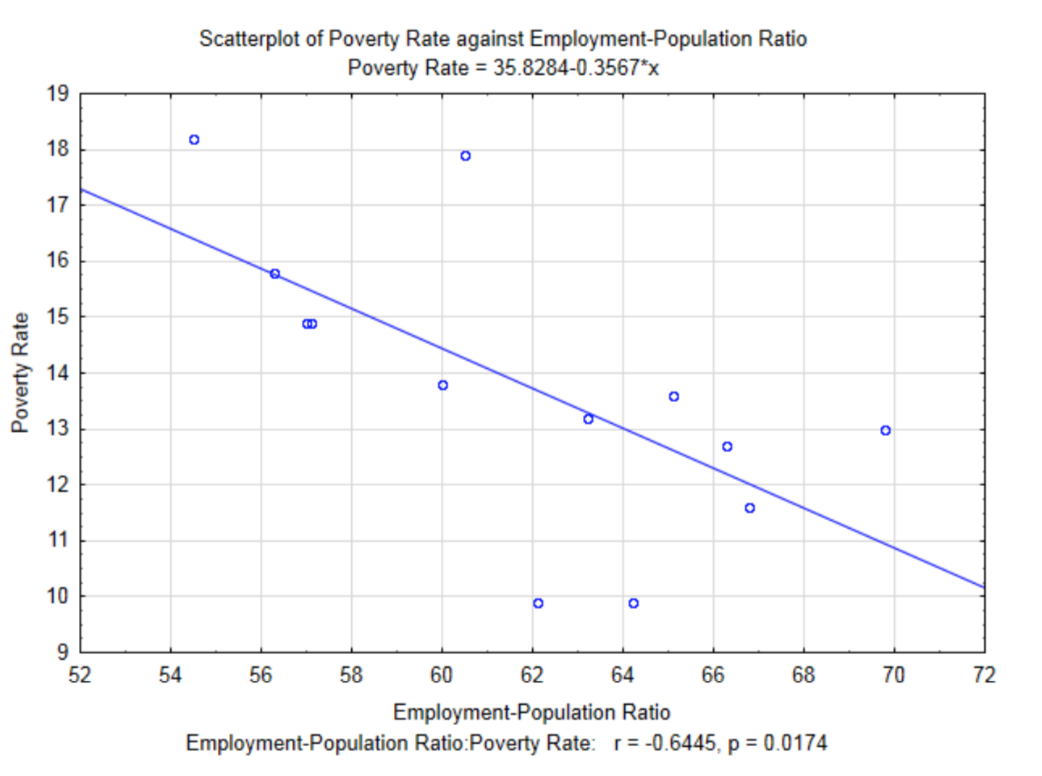
La ecuación de la línea, tal y como aparece en el subtítulo de la gráfica es\(y = 35.8284 – 0.3567x\), donde\(x\) está la Relación Empleo-Población y\(y\) es la tasa de pobreza. Como estudiante de álgebra, te enseñaron que una ecuación lineal se puede escribir en forma de\(y = mx + b\). En estadística, las ecuaciones de regresión lineal se escriben en la forma\(y = b + mx\) excepto que tradicionalmente se muestran como\(y' = a + bx\) donde\(y'\) representa el valor y predicho por la línea,\(a\) representa la\(y\) intersección y\(b\) representa la pendiente.
Para calcular los valores de\(a\) y\(b\), primero se necesitan otros 5 valores. Estas son la correlación (r), la media y desviación estándar para\(x\) (\(\bar{x}\)y\(s_x\)) y la media y desviación estándar para\(y\) (\(\bar{y}\)y\(s_y\)). Primero encuentra\(b\) usando la fórmula:\(b = r(\dfrac{s_y}{s_x})\). A continuación, sustituya\(\bar{y}\)\(\bar{x}\), y\(b\) en la ecuación lineal básica\(\bar{y} = a + b\bar{x}\) y resuelva para\(a\).
Para este ejemplo\(r = -0.6445\),\(bar{x} = 61.76\),\(s_x = 4.67\),\(bar{y} = 13.80\), y\(s_y = 2.58\).
\(b = r(\dfrac{s_y}{s_x})\)
\(b = -0.6445(\dfrac{2.58}{4.67}) = -0.3561\)
\(\bar{y} = a + b\bar{x}\)
\(1380 = a + -0.3561(61.76)\)
\(a = 35.79\)
Por lo tanto, la ecuación de regresión final es\(y' = 35.79 - 0.3561x\). La diferencia entre esta ecuación y la de la gráfica es el resultado de los errores de redondeo utilizados para estos cálculos.
La ecuación de regresión nos permite estimar el valor y, pero no proporciona una indicación de la precisión de la estimación. En otras palabras, ¿cuál es el efecto de la relación entre\(x\) y\(y\) sobre el\(y\) valor?
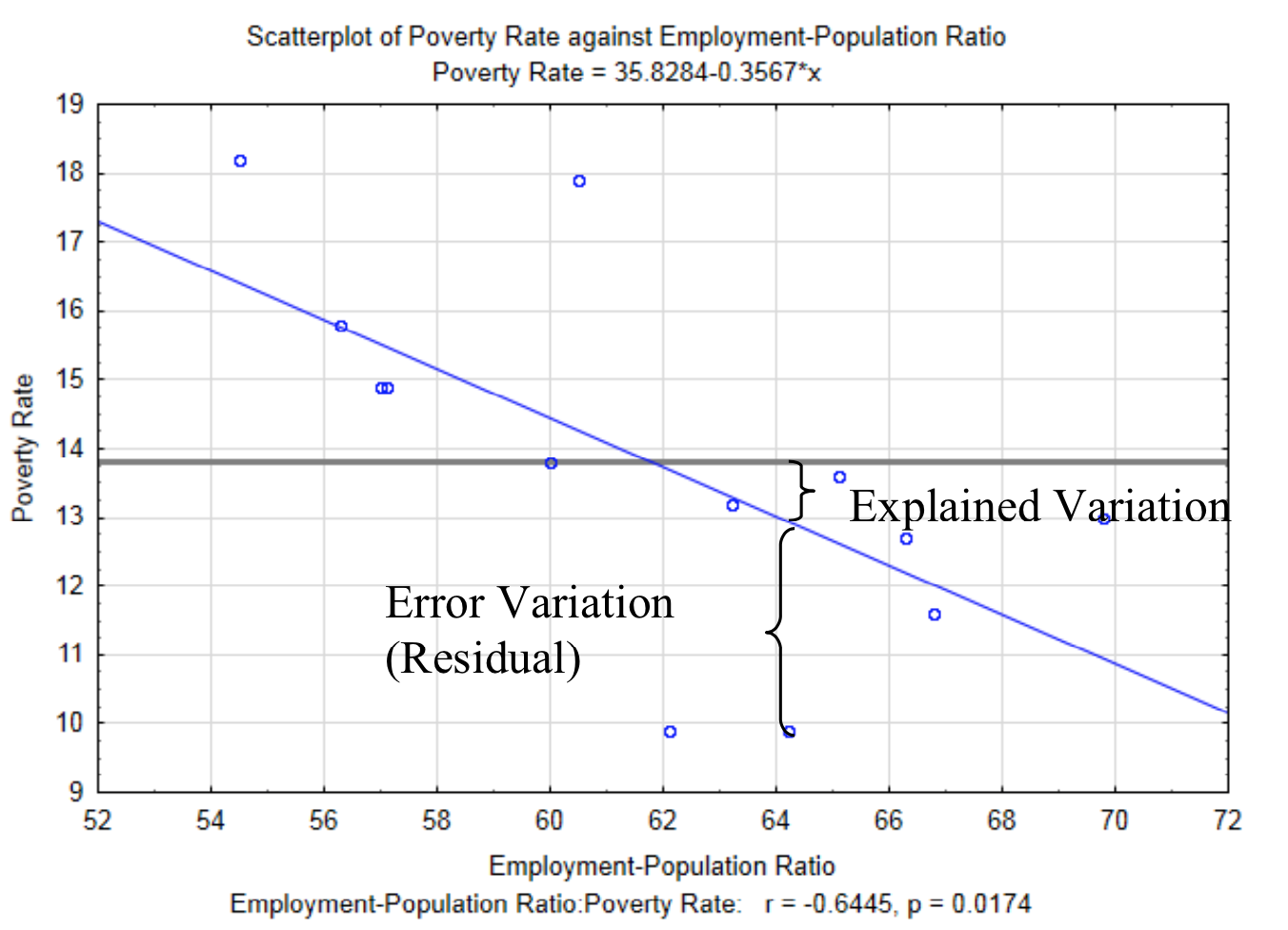
Determinar la influencia de la relación entre\(x\) y\(y\) comienza con la idea de que existe variación entre el\(y\) valor y la media de todos los\(y\) valores (\(bar{y}\)). Esto es algo que has visto con datos cuantitativos univariados. Hay dos razones por las que los\(y\) valores no son equivalentes a la media. Estos se denominan variación explicada y variación de error. La variación explicada es la variación que es consecuencia de la relación que\(y\) tiene con\(x\). En otras palabras,\(y\) no equivale a la media de todos los\(y\) valores porque la relación que muestra la línea de regresión influye en ella. La variación de error es la variación entre un punto real y el\(y\) valor predicho por la línea de regresión que es consecuencia de todos los demás factores que impactan en la variable aleatoria de respuesta. Esta distancia vertical entre cada punto de datos real y el\(y\) valor predicho (\(y'\)) se denomina residual. La variación explicada y la variación de error se muestran en la gráfica siguiente. La línea horizontal a 13.8 es la media de todos los\(y\) valores.
La variación total viene dada por la suma de la distancia cuadrada que cada valor es del\(y\) valor promedio. Esto se muestra como\(\sum_{i = 1}^{n} (y_i - \bar{y})^2\).
La variación explicada viene dada por la suma de las distancias cuadradas el\(y\) valor predicho por la ecuación de regresión (\(y'\)) es del\(y\) valor promedio,\(\bar{y}\). Esto se muestra como
\[\sum_{i = 1}^{n} (y_i' - \bar{y})^2.\]
La variación del error viene dada por la suma de las distancias cuadradas que el valor real de\(y\) los datos proviene del\(y\) valor predicho (\(y'\)). Esto se muestra como\(\sum_{i = 1}^{n} (y_i - y_i ')^2\).
La relación entre estos se puede mostrar con una ecuación de palabras y una ecuación algebraica.
Variación Total = Variación Explicada + Variación de Error
\[\sum_{i = 1}^{n} (y_{i} - \bar{y})^{2} = \sum_{i = 1}^{n} (y_{i}' - \bar{y})^{2} + \sum_{i = 1}^{n} (y_{i} - y_{i} ')^2\]
La razón principal de esta discusión es llevarnos a una comprensión de la influencia matemática (aunque no necesariamente causal) de la\(x\) variable sobre la\(y\) variable. Dado que esta influencia es la variación explicada, entonces podemos encontrar la relación entre la variación explicada y la variación total. Definimos esta relación como el coeficiente de determinación. La relación está representada por\(r^2\).
\(r^2 = \dfrac{\sum_{i = 1}^{n} (y_i' - \bar{y})^2}{\sum_{i = 1}^{n} (y_i - \bar{y})^2}\)
El coeficiente de determinación es el cuadrado del coeficiente de correlación. Lo que representa es la proporción de la varianza de una variable que resulta de la influencia matemática de la varianza de la otra variable. El coeficiente de determinación siempre será un valor entre 0 y 1, es decir\(0 \le r^2 \le 1\). Si bien\(r^2\) se presenta de esta manera, a menudo se habla de ello en términos de porcentaje, lo que resulta multiplicando el\(r^2\) valor por 100.
En el diagrama de dispersión de la tasa de pobreza frente a la relación empleo-población, la correlación es\(r = - 0.6445\), así\(r^2 = 0.4153\). Por lo tanto, concluimos que 41.53% de la influencia en la varianza en la tasa de pobreza proviene de la varianza en la relación empleo-población. La influencia restante que se considera variación de error proviene de algunos de los otros ítems de la lista de posibles variables que podrían afectar la pobreza.
No existe una escala definitiva para determinar los niveles deseables para\(r^2\). Mientras que los valores cercanos a 1 muestran una fuerte relación matemática y los valores cercanos a 0 muestran una relación débil, el investigador debe contemplar el significado real del\(r^2\) valor en el contexto de su investigación.
Tecnología
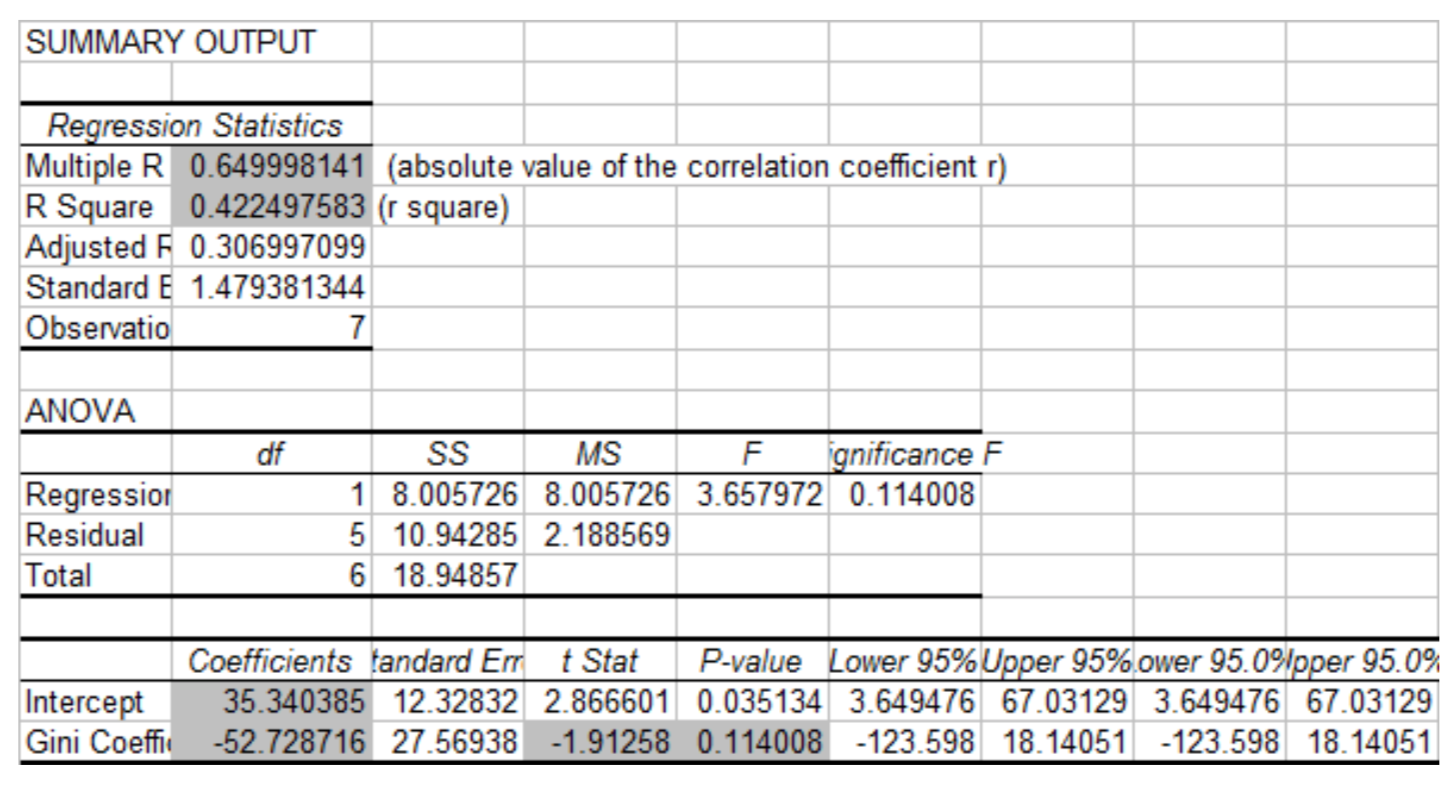
Calcular ecuaciones de correlación y regresión a mano puede ser muy tedioso y estar sujeto a errores de redondeo. En consecuencia, la tecnología se emplea rutinariamente en el análisis de regresión. Aquí se utilizarán los datos que se utilizaron al comparar los Coeficientes de Gini con las tasas de pobreza.
| Coeficiente de Gini | Tasa de Pobreza |
|---|---|
| 0.486 | 10.1 |
| 0.443 | 9.9 |
| 0.44 | 11.6 |
| 0.433 | 13 |
| 0.419 | 13.2 |
| 0.442 | 14.4 |
| 0.464 | 10.3 |
ti 84 Calculadora
Para ingresar los datos, use Stat — Edit — Enter para llegar a las listas que se utilizaron en el Capítulo 4. Borrar enumera uno y dos moviendo el cursor hacia arriba hasta L1, presionando el botón de borrar y luego moviendo el cursor hacia abajo. Haz lo mismo para L2.
Ingresar los Coeficientes de Gini en L1, la Tasa de Pobreza en L2. Deben permanecer emparejados de la misma manera que están en la tabla.
Para determinar el valor de t, el valor p, los valores r y r2 y los valores numéricos en la ecuación de regresión, utilice Stat — Tests — E: LineGetTest. Ingresa la Xlist como L1 y la Ylist como L2. La hipótesis alternativa se muestra como\(\beta\) &\(\rho\):\(\ne\) 0. Coloque el cursor sobre Calcular y presione enter.
La salida es:
LineGetTest
\(y = a + bx\)
\(\beta \ne 0\) y\(\rho \ne 0\)
t = -1.912582657
p = 0.1140079665
df = 5
b = -52.72871602
\(s = 1.479381344\) (error estándar)
\(r^2 = 0.4224975727\)
\(r = -0.6499981406\)
El Excel de Microsoft contiene un complemento que debe ser instalado para completar el análisis de regresión. En versiones más recientes de Excel (2010), este complemento puede ser instalado por
- Seleccione la pestaña de archivo
- Seleccionar opciones
- En el lado izquierdo, seleccione Complementos
- En la parte inferior, junto a donde dice Complementos de Excel, haga clic en Ir Marque la primera casilla, que dice Herramientas de análisis luego haga clic en Aceptar. Es posible que necesite su disco Excel en este punto.
Para hacer el Análisis real:
- Seleccione la pestaña de datos
- Seleccione la opción de análisis de datos (cerca de la parte superior derecha de la pantalla)
- Seleccione Regresión
- Rellene los espacios para los rangos de datos y y x.
- Haga clic en Aceptar.
Se creará una nueva hoja de trabajo que contenga una salida de resumen. Algunos de los números se muestran en gris para ayudarte a saber qué números buscar. Observe cómo corresponden a la salida del TI 84 y a los cálculos realizados anteriormente en este capítulo.