Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

8: Plaza Chi

Última actualización

31 oct 2022
Guardar como PDF
- 7.E: Análisis de Datos Cuantitativos Bivariados (Ejercicios)
- 8.E: Chi Cuadrado (Ejercicios)

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

En el capítulo 5, se desarrolló la teoría inferencial para datos categóricos con base en la distribución binomial. Recordemos que la distribución binomial muestra la probabilidad del posible número de éxitos en una muestra de tamaño n cuando solo hubo dos posibles resultados independientes, éxito y fracaso. Sin embargo, ¿qué sucede si hay más de dos posibles resultados?

Considera las siguientes tres preguntas.

¿La calculadora TI 84 genera números iguales de 0-9 al usar el generador de enteros aleatorios?
Hacer algo sobre el cambio climático ha sido un reto para la humanidad. El sitio web Edge.Org tenía una propuesta presentada por Lee Smolin, físico del Instituto Perimeter y autor del libro Time Reborn. (www.edge.org/conversation/del... ooperation/ #rc 30 de nov de 2013.) La esencia de la propuesta es que se debe colocar un impuesto al carbono sobre todo el carbono que se utilice pero en lugar de que el dinero vaya al gobierno va a cuentas individuales de jubilación climática. Cada persona tendría esa cuenta. Cada cuenta tendría dos categorías de posibles inversiones que un individuo podría elegir. Las inversiones de categoría A serían en cosas que mitiguen el cambio climático (por ejemplo, solar, eólica, etc.). Las inversiones de categoría B estarían en cosas que podrían funcionar bien si no ocurre el cambio climático (por ejemplo, servicios públicos que queman carbón, desarrollos inmobiliarios costeros y empresas de automóviles que no producen autos eficientes en combustible o eléctricos). ¿Existe correlación entre la opinión de una persona sobre el cambio climático y su elección de inversión?
Los huracanes se clasifican en la categoría 1,2,3,4,5. ¿Es diferente la distribución de los huracanes en los años 1951- 2000 de lo que era en 1901-1950?

Antes de que se pueda hacer un análisis, es necesario comprender el tipo de datos que se recogen para cada una de estas preguntas.

En la pregunta 1, los datos que se recopilarán son los números 0 a 9. Si bien los números suelen considerarse cuantitativos, en este caso simplemente queremos saber si la calculadora produce cada número específico. Por lo tanto, en realidad se trata de la frecuencia con la que se producen estos números. Si el proceso utilizado por la calculadora es suficientemente aleatorio, entonces las frecuencias para todos los números deberían ser iguales si se toma una muestra lo suficientemente grande. Entonces, a pesar de parecer datos cuantitativos, en realidad se trata de datos categóricos, con 10 categorías diferentes y siendo los datos que se seleccionó un número.

En la pregunta 2, imagina una encuesta de dos preguntas en la que se haga a la gente:

¿Crees que el cambio climático está ocurriendo porque los humanos han estado usando fuentes de carbono que llevan a un aumento de los gases de efecto invernadero? Sí No
¿Cuál de las siguientes representa más de cerca la elección que tomaría para las inversiones de su cuenta de jubilación climática individual? Categoría A Categoría B

Para esta pregunta, hay una población. Cada persona que realice la encuesta proporcionaría dos respuestas. El objetivo es determinar si existe correlación entre su opinión sobre el cambio climático y su elección de inversión. Una forma alternativa de decir esto es que las dos variables son independientes entre sí, lo que significa que una respuesta no afecta a la otra, o no son independientes lo que significa que la opinión sobre el cambio climático y la estrategia de inversión están relacionadas.

En la pregunta 3, hay dos poblaciones. La primera población es huracanes en 1901-50 y la segunda población es huracanes en 1951-2000. Hay 5 categorías de huracanes y el objetivo es ver si la distribución de huracanes en estas categorías es la misma o diferente.

Los problemas se ajustan a una de las siguientes clases de problemas, en orden: bondad de ajuste, prueba de independencia y prueba de homogeneidad. A continuación se muestra el uso de estos problemas y sus hipótesis.

Bondad de ajuste

La prueba de bondad de ajuste se utiliza cuando una variable aleatoria categórica con más de dos niveles tiene una distribución esperada.

$H_0$ : La distribución es la misma que se esperaba

$H_1$ : La distribución es diferente a la esperada
Prueba de independencia

La prueba de independencia se utiliza cuando existen dos variables aleatorias categóricas para una misma unidad (o persona) y el objetivo es determinar una correlación entre ellas.

$H_0$ : Las dos variables aleatorias son independientes (sin correlación)

$H_1$ : Las dos variables aleatorias no son independientes (correlación)

Si los datos son significativos, que el conocimiento de la de una de las variables aleatorias aumenta la probabilidad de conocer el valor de la otra variable aleatoria en comparación con el azar.
Prueba de homogeneidad
La prueba de homogeneidad se utiliza cuando hay muestras tomadas de dos (o más) poblaciones con el objetivo de determinar si la distribución de una variable aleatoria es similar o diferente en las dos poblaciones.

$H_0$ : Las dos poblaciones son homogéneas

$H_1$ : Las dos poblaciones no son homogéneas

Dado que todos los problemas tienen datos que se pueden contar exactamente una vez, la estrategia es determinar en qué se diferencia la distribución de los recuentos de la distribución esperada. El análisis de todos estos problemas utiliza la misma fórmula estadística de prueba llamada $chi ^2$ (Chi Square).

$\chi^2 = \sum \dfrac{(O - E)^2}{E}$
La distribución que se utiliza para probar las hipótesis es el conjunto de $chi ^2$ distribuciones. Estas distribuciones están sesgadas positivamente. No pueden ser negativos. Cada distribución se basa en el número de grados de libertad. A diferencia de las distribuciones t en las que los grados de libertad se basaron en el tamaño de la muestra, en el caso de $chi ^2$ , los grados de libertad se basan en el número de niveles de la (s) variable (s) aleatoria (s).

Las siguientes distribuciones muestran 10,000 muestras de tamaño n = 100 en las que se calcularon y graficaron los estadísticos de $chi ^2$ prueba. Los números de grados de libertad en estas cuatro gráficas son 1,2,5, y 9.

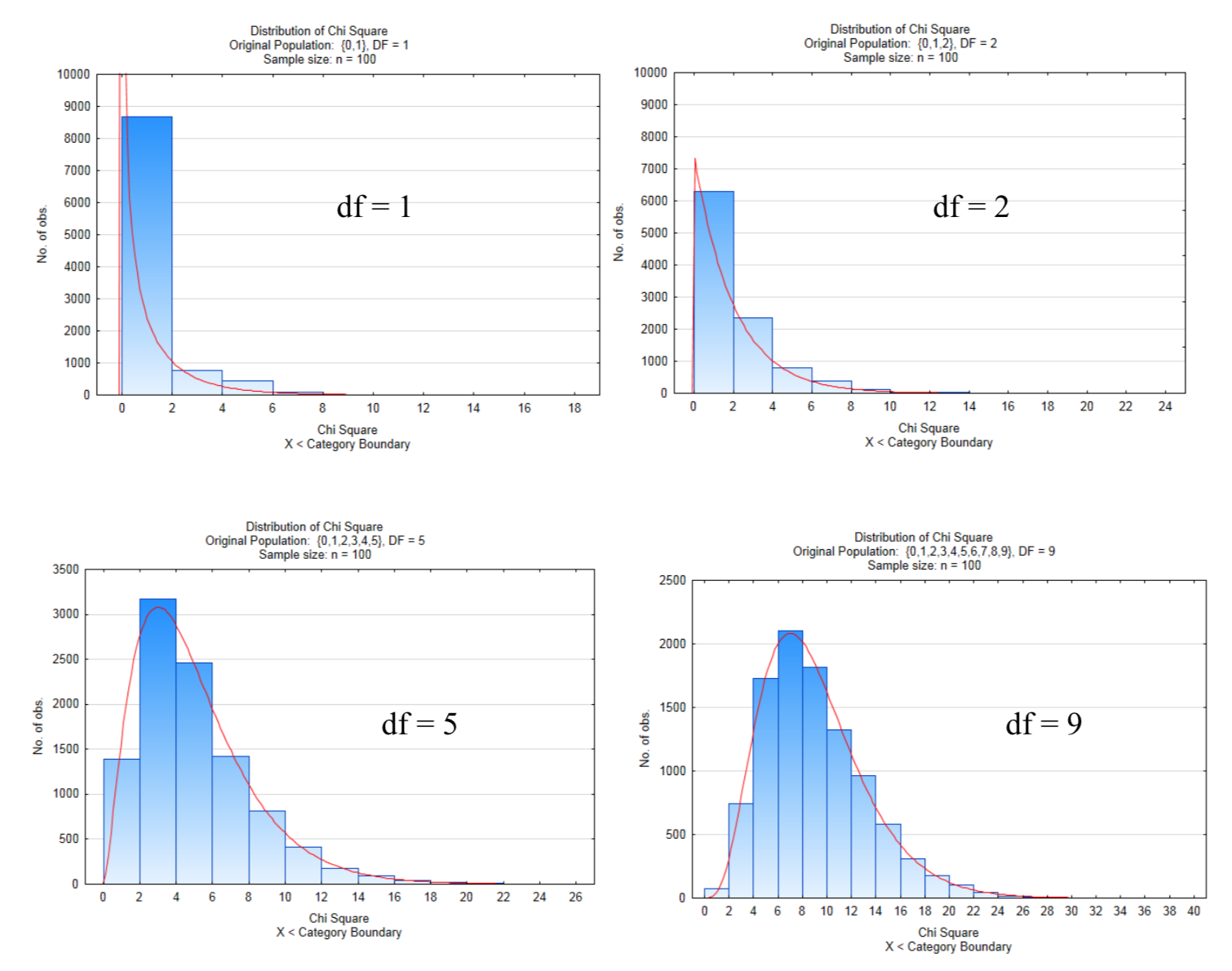
2019-05-17 1.50.05.png

Observe cómo la distribución de Chi Square se vuelve menos sesgada y se acerca a una distribución normal a medida que aumenta el número de grados de libertad. Un incremento en el número de grados de libertad corresponde a un incremento en el número de niveles del factor explicativo. La manera en que se encuentran los grados de libertad es diferente para la prueba de bondad de ajuste en comparación con la prueba de independencia y prueba de homogeneidad. Cada método se explicará a su vez.

Prueba de bondad de ajuste

1. ¿La calculadora TI 84 genera números iguales de 0-9 al usar el generador de enteros aleatorios?

En este experimento, 12 números entre 1 y 100 fueron generados aleatoriamente por la calculadora TI 84. Estos 12 números se utilizaron como valores de semilla. Después de sembrar la calculadora con cada número, se generaron aleatoriamente 10 números nuevos entre 0 y 9 usando la función randint en la calculadora. Así, se produjeron un total de 120 números entre 0 y 9. La frecuencia de estos números se muestra en la tabla siguiente.

0	1	2	3	4	5	6	7	8	9
15	11	12	14	10	14	10	11	14	9

Las hipótesis a probar son:

$H_0$ : La frecuencia de celda observada es igual a la frecuencia celular esperada para todas las celdas

$H_1$ : La frecuencia celular observada no es igual a la frecuencia celular esperada para al menos una celda. Usar un nivel de significancia 0.05

Esto se puede representar simbólicamente como

$H_0$ : $o_1 = \epsilon_1$ para todas las celdas

$H_1$ : $o_1 \ne \epsilon_1$ para al menos una celda

donde ο es la letra griega minúscula omicron que representa la frecuencia celular observada en la población subyacente y ε es la letra griega minúscula épsilon que representa la frecuencia celular esperada. La frecuencia celular esperada siempre debe ser 5 o superior. Si no lo es, las células deben reagruparse.

La tabla anterior muestra las frecuencias observadas, pero ¿cuáles son las frecuencias esperadas? En teoría, si el proceso es verdaderamente aleatorio, entonces cada número ocurriría con la misma frecuencia si el muestreo se hiciera un número muy grande de veces. Si este es el caso, entonces en una muestra de tamaño 120, con 10 alternativas posibles, el número esperado de frecuencias para cada alternativa debe ser 12. De la tabla, vemos que la mayoría de las frecuencias no son 12, pero lo que se necesita es una manera de determinar si la cantidad de variación que existe es suficiente para sugerir que las frecuencias observadas no son iguales a las frecuencias esperadas. Tal conclusión implicaría que la calculadora no produce un conjunto verdaderamente aleatorio de números. La estrategia es encontrar $\chi^2$ y luego usar la $\chi^2$ distribución adecuada para encontrar el valor p. Una forma de encontrar $\chi^2 = \sum \dfrac{(O - E)^2}{E}$ es con una mesa.

Observado	Esperado	O - E	$(O - E)^2$	$\dfrac{(O - E)^2}{E}$
15	12	3	\ ((O - E) ^2\)” style="vertical-align:middle; ">9	\ (\ dfrac {(O - E) ^2} {E}\)” style="vertical-align:middle; "> $\dfrac{9}{12}$
11	12	-1	\ ((O - E) ^2\)” style="vertical-align:middle; ">1	\ (\ dfrac {(O - E) ^2} {E}\)” style="vertical-align:middle; "> $\dfrac{1}{12}$
12	12	0	\ ((O - E) ^2\)” style="vertical-align:middle; ">0	\ (\ dfrac {(O - E) ^2} {E}\)” style="vertical-align:middle; "> $\dfrac{0}{12}$
14	12	2	\ ((O - E) ^2\)” style="vertical-align:middle; ">4	\ (\ dfrac {(O - E) ^2} {E}\)” style="vertical-align:middle; "> $\dfrac{4}{12}$
10	12	-2	\ ((O - E) ^2\)” style="vertical-align:middle; ">4	\ (\ dfrac {(O - E) ^2} {E}\)” style="vertical-align:middle; "> $\dfrac{4}{12}$
14	12	2	\ ((O - E) ^2\)” style="vertical-align:middle; ">4	\ (\ dfrac {(O - E) ^2} {E}\)” style="vertical-align:middle; "> $\dfrac{4}{12}$
10	12	-2	\ ((O - E) ^2\)” style="vertical-align:middle; ">4	\ (\ dfrac {(O - E) ^2} {E}\)” style="vertical-align:middle; "> $\dfrac{4}{12}$
11	12	-1	\ ((O - E) ^2\)” style="vertical-align:middle; ">1	\ (\ dfrac {(O - E) ^2} {E}\)” style="vertical-align:middle; "> $\dfrac{1}{12}$
14	12	2	\ ((O - E) ^2\)” style="vertical-align:middle; ">4	\ (\ dfrac {(O - E) ^2} {E}\)” style="vertical-align:middle; "> $\dfrac{4}{12}$
9	12	-3	\ ((O - E) ^2\)” style="vertical-align:middle; ">9	\ (\ dfrac {(O - E) ^2} {E}\)” style="vertical-align:middle; "> $\dfrac{9}{12}$
			\ ((O - E) ^2\)” style="vertical-align:middle; ">	\ (\ dfrac {(O - E) ^2} {E}\)” style="vertical-align:middle; "> $\chi^2 = \dfrac{40}{12} = 3.33$

Si r representa el número de filas, entonces el número de grados de libertad en una prueba de bondad de ajuste es:

df = r — 1.

Para esta prueba de bondad de ajuste, hay 10 filas de datos. En consecuencia hay 9 grados de libertad.

El valor p para se $\chi^2$ puede encontrar usando la tabla de las Distribuciones de Chi Cuadrado al final de este capítulo o su calculadora.

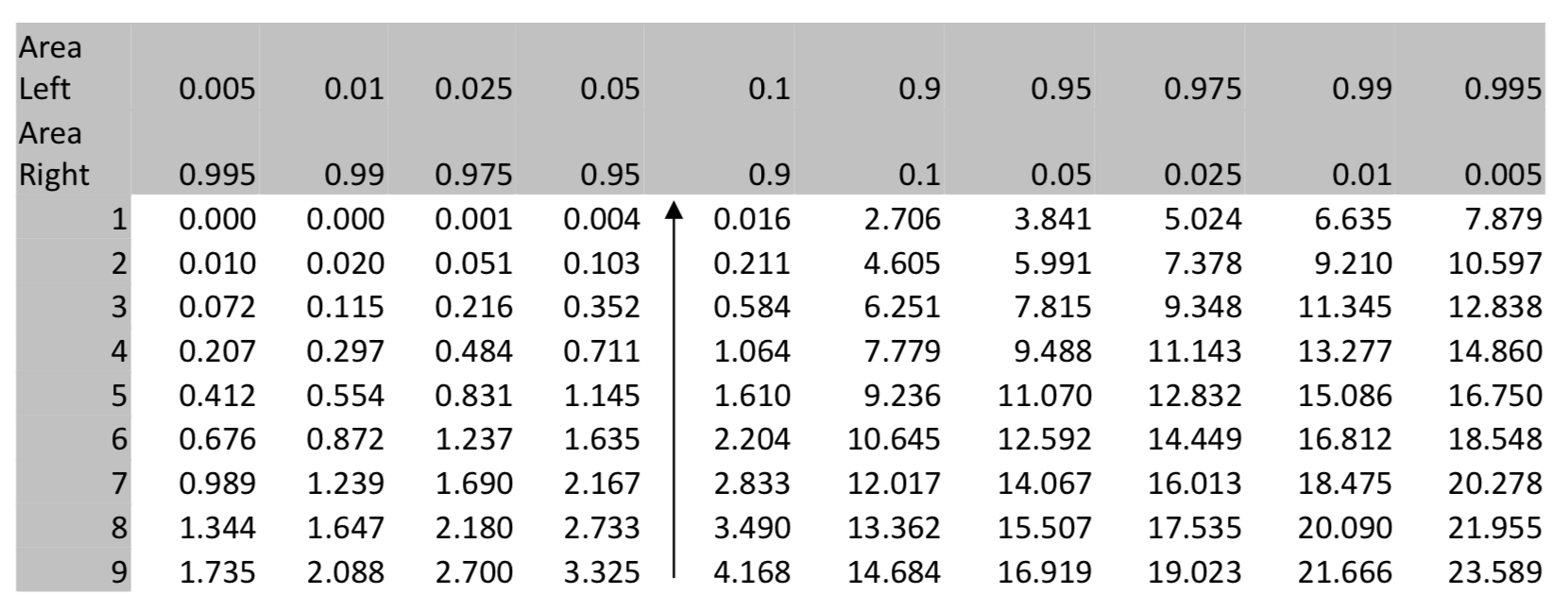
Las Distribuciones Chi-Cuadradas también se pueden utilizar para encontrar el valor p. Usando la siguiente tabla, encuentra los grados de libertad en la columna izquierda, localiza el $\chi^2$ valor en la fila, luego mueve a la fila que muestra el área a la derecha y usa un signo de desigualdad para mostrar el valor p. Si el valor p es mayor que $\alpha$ , entonces use el símbolo mayor que. Si es menor que α, use el símbolo menor que, pero en cualquier caso, use la mayor precisión posible. Por ejemplo, si α es 0.05 pero el área a la derecha es menor que 0.025, entonces se prefiere p < 0.025 sobre p < 0.05.

En este ejemplo, $\chi^2$ = 3.33, hay 9 grados de libertad, por lo que el valor p > 0.9.

2019-05-17 2.03.02.png

$\chi^2 = 3.33$

El uso de $\chi^2$ cdf (bajo, alto, df) en la calculadora TI 84 da como resultado $\chi^2$ cdf (3.33, 1E99,9) = 0.9496.

Dado que este valor p es claramente superior a 0.05, se puede escribir la conclusión:

Al nivel de significancia del 5%, los valores de celda observados no son significativamente diferentes a los valores esperados de celda ( $\chi^2$ = 3.33, p = 0.9496, df=9). La calculadora TI84 parece producir un buen conjunto de enteros aleatorios.

En el caso de la calculadora, si es aleatoria en la generación de números, esperaríamos el mismo número de valores en cada categoría. Es decir, esperaríamos obtener el mismo número de 0s, 1s, 2s, etc. ya que la muestra consistió en 120 ensayos con 10 posibilidades para cada resultado, el valor esperado es 12 porque 120 dividido por 10 es 12. Pero, ¿qué pasa si el resultado esperado no es el mismo en todos los casos?

En el otoño de 2013, nuestro colegio estaba conformado por 54% caucásicos, 14% hispano/latinos, 11% afroamericanos, 10% asiáticos/isleños del Pacífico, 1% nativos americanos, 3% internacionales y 7% otros. Si quisiéramos determinar si la distribución racial/étnica de los estudiantes de estadística es diferente a la de toda la escuela, podríamos realizar una encuesta a los estudiantes de estadística para obtener los datos observados. La siguiente tabla contiene datos hipotéticos observados. Ya que hay 300 alumnos en la muestra y con base en la matrícula universitaria, 54% del cuerpo estudiantil es blanco, entonces el número esperado de alumnos en la clase que son blancos se encuentra multiplicando 300 por 0.54. Se toma el mismo enfoque para cada carrera. Esto se muestra en la tabla. Observe que el total en la columna esperada es el mismo que en la columna observada.

Raza/Etnicidad	Observado	Esperado
Caucásico/blanco (54%)	154	0.54 (300) = 162
H ispánico/Latino (14%)	48	0.14 (300) = 42
Un fricano americano/negro (11%)	36	0.11 (300) = 33
Un siano/isleño del Pacífico (10%)	35	0.10 (300) = 30
Nativo Americano (1%)	6	0.01 (300) = 3
Internacional (3%)	9	0.03 (300) = 9
Otros (7%)	12	0.07 (300) = 21
Total	300	Total 300

El resto de la prueba de bondad de ajuste se realiza igual que con el ejemplo de la calculadora y no se demostrará aquí.

Prueba de la Plaza Chi para la Independencia

La Prueba de Chi Cuadrado para la Independencia se utiliza cuando un investigador quiere determinar una relación entre dos variables categóricas aleatorias recolectadas en una misma unidad (o persona). Las preguntas de muestra incluyen:

¿Existe una relación entre la afiliación religiosa de una persona y su preferencia de partido político?
¿Existe una relación entre la disposición de una persona a comer alimentos genéticamente modificados y su disposición a usar la medicina genéticamente modificada?
¿Existe una relación entre el campo de estudio de un egresado universitario y su capacidad de pensar críticamente?
¿Existe una relación entre la calidad del sueño que recibe una persona y su actitud durante el día siguiente?

Como ejemplo, aprenderemos la mecánica de la prueba para la independencia utilizando el ejemplo hipotético de respuestas a las dos preguntas sobre cambio climático e inversiones.

¿Crees que el cambio climático está ocurriendo porque los humanos han estado usando fuentes de carbono que llevan a un aumento de los gases de efecto invernadero? Sí No
¿Cuál de las siguientes representa más de cerca la elección que tomaría para las inversiones de su cuenta de jubilación climática individual? Categoría A Categoría B

Categoría A — solar, eólica Categoría B — Carbón, desarrollo del lado del océano

$H_0$ : Las dos variables aleatorias son independientes (sin correlación)
$H_1$ : Las dos variables aleatorias no son independientes (correlación)

Esto también se puede representar simbólicamente como

$H_0: o_1 = \epsilon_1$ para todas las células
$H_1: o_1 \ne \epsilon_1$ para al menos una célula
donde $o$ está la letra griega minúscula omicron que representa la frecuencia celular observada en la población subyacente y $\epsilon$ es la letra griega minúscula épsilon que representa la célula esperada frecuencia. La frecuencia celular esperada siempre debe ser 5 o superior. Si no lo es, las células deben reagruparse.

Utilizar un nivel de significancia de 0.05.

Debido a que esto se hará con datos simulados, será útil hacerlo dos veces, produciendo conclusiones opuestas cada vez.

Los datos se presentarán en una tabla de contingencia 2 x 2.

Versión 1 Observada	Sí, los humanos contribuyen al cambio climático	No, los humanos no contribuyen al cambio climático	Totales
Categoría A Inversiones (eólica, solar)	56	54
Categoría B Inversiones (carbón, desarrollos de costa oceánica)	47	43
Total

La prueba de independencia utiliza la misma fórmula que la prueba de bondad de ajuste. $\chi^2 = \sum \dfrac{(O - E)^2}{E}$ . Sin embargo, a diferencia de esa prueba, no hay una indicación clara de cuáles son los valores esperados. En cambio deben calcularse, que es un proceso de cuatro pasos.

Paso 1, Encuentra los totales de fila y columna y el total general.

Versión 1 Observada	Sí, los humanos contribuyen al cambio climático	No, los humanos no contribuyen al cambio climático	Totales
Categoría A Inversiones (eólica, solar)	56	54	110
Categoría B Inversiones (carbón, desarrollos de costa oceánica)	47	43	90
Total	103	97	200

Paso 2. Crear una nueva tabla para los valores esperados. El proceso de razonamiento para calcular los valores esperados consiste en considerar primero la proporción de todos los valores que caen en cada columna. En la primera columna hay 103 valores de 200 que es $\dfrac{}{} = 0.515$ . En la segunda columna hay 97 de 200 valores (0.485). Dado que 51.5% de los valores están en la primera columna, entonces se esperaría que 51.5% de los valores de la primera fila también estarían en la primera columna. Así, 0.515 (110) da un valor esperado de 56.65. De igual manera, 0.485 (90) producirá el valor esperado de 43.65 para la última celda. Como fórmula, esto se puede expresar como

$\dfrac{Column\ Total}{Grand\ Total} \cdot Row\ Total$

Versión 1 Observada	Sí, los humanos contribuyen al cambio climático	No, los humanos no contribuyen al cambio climático	Totales
Categoría A Inversiones (eólica, solar)	$\dfrac{103}{200} \cdot 110 = 56.65$	$\dfrac{97}{200} \cdot 110 = 53.35$	110
Categoría B Inversiones (carbón, desarrollos de costa oceánica)	$\dfrac{103}{200} \cdot 90 = 46.35$	$\dfrac{97}{200} \cdot 110 = 43.65$	90
Total	103	97	200

Paso 3. Use una tabla similar a la utilizada en la prueba de Bondad de Ajuste para calcular el Chi Cuadrado.

Observado	Esperado	$O - E$	$(O - E)^2$	$\dfrac{(O - E)^2}{E}$
56	56.65	-0.65	0.4225	0.0075
54	53.35	0.65	0.4225	0.0079
47	46.35	0.65	0.4225	0.0091
43	43.65	-0.65	0.4225	0.0097
				$\chi^2 = 0.0342$

Paso 4. Determinar los grados de libertad y encontrar el valor p

Si R es el número de Filas en la Tabla de contingencia y C es el número de columnas en la tabla de contingencia, entonces el número de grados de libertad para la prueba de independencia se encuentra como

df = (R - 1) (C - 1).

Para una tabla de contingencia de 2 x 2 como en este problema, solo hay 1 grado de libertad porque (2-1) (2-1) = 1.

El valor p para se $\chi^2$ puede encontrar usando la tabla o su calculadora.

En la tabla ubicamos 0.034 en la fila con 1 grado de libertad, luego nos movemos hacia arriba a la fila para el área a la derecha. Dado que el área a la derecha es mayor que 0.05, pero más específicamente es mayor que 0.1, el valor p se escribe como p > 0.1.

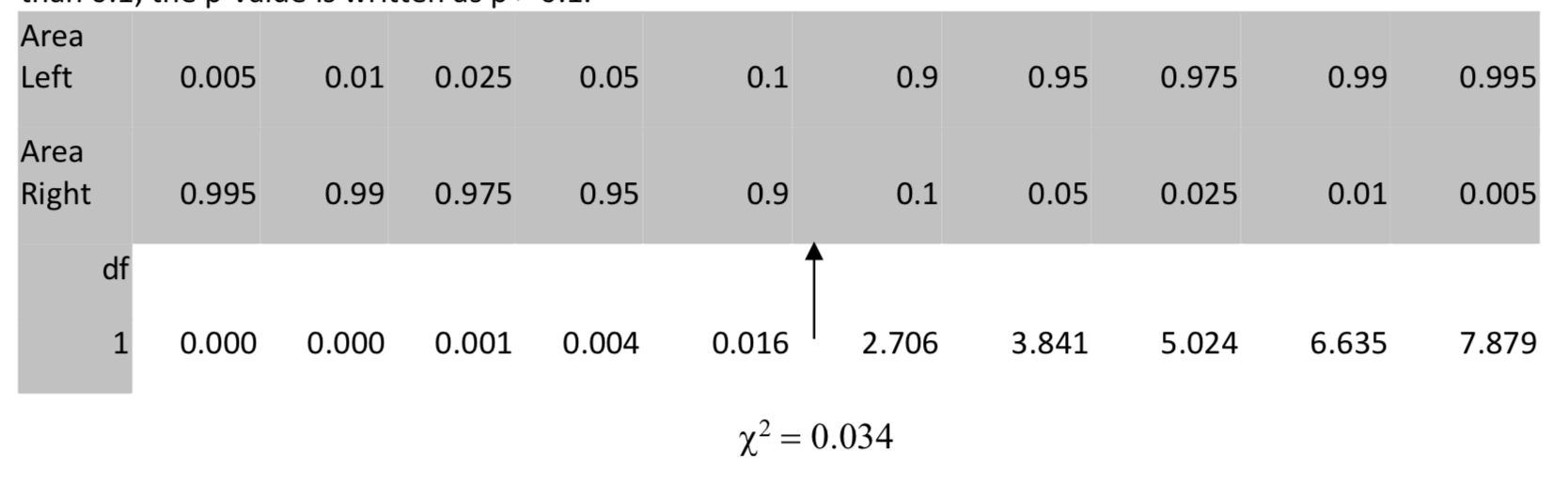
2019-05-17 2.34.09.png

En tu calculadora, usa $\chi^2$ cdf (bajo, alto, df). En este caso, $\chi^2$ cdf (0.0342, 1E99, 1) = 0.853.

Dado que los datos no son significativos, concluimos que la estrategia de inversión de las personas es independiente de su opinión sobre las contribuciones humanas al cambio climático.

La versión 2 de este problema utiliza la siguiente tabla de contingencia.

Versión 2 Observada	Sí, los humanos contribuyen al cambio climático	No, los humanos no contribuyen al cambio climático	Totales
Categoría A Inversiones (eólica, solar)	80	30
Categoría B Inversiones (carbón, desarrollos de costa oceánica)	30	60
Total

Esta vez, todo el problema se calculará usando la calculadora TI 84 en lugar de construir las tablas que se utilizaron en la Versión 1.

Paso 1. Matriz
Paso 2. Configura 1: [A] en una matriz de 2 x 2 seleccionando Editar Entrar y luego modificar la R x C según sea necesario. Paso 3. Ingresa las frecuencias tal y como se muestran en la tabla.
Paso 4. STAT TEST $\chi^2$ − Test
Observado: [A]
Esperado: [B] (no es necesario crear la matriz Esperada, la calculadora lo hará para usted.)
Seleccione Calcular para ver los resultados:
$\chi^2$ = 31.03764922
p=2.5307155e-8
df=1

En este caso, los datos son significativos. Esto significa que existe una correlación entre la opinión de cada persona sobre las contribuciones humanas al cambio climático y su elección de inversiones. Recuerda que la correlación no es causalidad.

Prueba de Chi Cuadrado para Homogeneidad

El tercer y último problema se refiere a la clasificación de los huracanes en dos décadas distintas, 1901-50 y 1951-2000. Una teoría sobre el cambio climático es que los huracanes podrían empeorar. ser trabajado usando tablas.

Los huracanes son clasificados por la Escala de Viento Huracanes Saffir-Simpson.2

Categoría 1 Vientos sostenidos 74-95 mph
Categoría 2 Vientos sostenidos 96-110 mph
Categoría 3 Vientos sostenidos 111-129 mph
Categoría 4 Vientos sostenidos 130-156 mph
Categoría 5 Vientos sostenidos 157 o superior.

Los huracanes de categoría 3, 4 y 5 se consideran importantes.

Este problema

La población de interés es la distribución de huracanes para las condiciones climáticas imperantes en su momento. Las hipótesis que se están probando son

$H_0$ : Las distribuciones son homogéneas

$H_1$ : Las distribuciones no son homogéneas

Esto también se puede representar simbólicamente como

$H_0: o_1 = \epsilon_1$ para todas las celdas
$H_1: o_1 \ne \epsilon_1$ para al menos una celda

donde $o$ es la letra griega minúscula omicron que representa la frecuencia celular observada en la población subyacente y $\epsilon$ es la letra griega minúscula épsilon que representa la frecuencia celular esperada. La frecuencia celular esperada siempre debe ser 5 o superior. Si no lo es, las células deben reagruparse.

Se utilizará una tabla de contingencia de 5 x 2 para mostrar las frecuencias que se observaron. Las frecuencias esperadas se calcularon de la misma manera que en la prueba de independencia. (http://www.nhc.noaa.gov/pastdec.shtml visto 12/7/13)

Observado	1901 - 1950	1951 - 2000	Totales
Categoría 1	37	29	66
Categoría 2	24	15	39
Categoría 3	26	21	47
Categoría 4	7	5	12
Categoría 5	1	2	3
Totales	95	72	167

Esperado	1901 - 1950	1951 - 2000	Totales
Categoría 1	37.54	28.46	66
Categoría 2	22.19	16.81	39
Categoría 3	26.74	20.26	47
Categoría 4	6.83	5.17	12
Categoría 5	1.71	1.29	3
Totales	95	72	167

Observe que las frecuencias celulares esperadas para huracanes de categoría 5 son menores a 5, por lo que será necesario que rehagamos este problema combinando grupos. El grupo 5 se combinará con el grupo 4 y se proporcionarán las tablas modificadas.

Observado	1901 - 1950	1951 - 2000	Total
Categoría 1	37	29	66
Categoría 2	24	15	39
Categoría 3	26	21	47
Categoría 4 y 5	8	7	15
Total	95	72	167

Observado	1901 - 1950	1951 - 2000	Total
Categoría 1	37.54	28.46	66
Categoría 2	22.19	16.81	39
Categoría 3	26.74	20.26	47
Categoría 4 y 5	8.53	6.47	15
Total	95	72	167

	Observado	Esperado	$O - E$	$(O - E)^2$	$\dfrac{(O - E)^2}{E}$
1901 - 50
Categoría 1	37	37.54	-0.54	0.30	0.008
Categoría 2	24	22.19	1.81	3.29	0.148
Categoría 3	26	26.74	-0.74	0.54	0.020
Categoría 4 y 5	8	8.53	-0.53	0.28	0.033
1951 - 2000
Categoría 1	29	28.46	0.54	0.30	0.010
Categoría 2	15	16.81	-1.81	3.29	0.196
Categoría 3	21	20.26	0.74	0.54	0.027
Categoría 4 y 5	7	6.47	0.53	0.28	0.044
					$\chi^2 = 0.487$

Si R es el número de Filas en la Tabla de contingencia y C es el número de columnas en la tabla de contingencia, entonces el número de grados de libertad para la prueba de homogeneidad se encuentra como

df = (R-1) (C-1).

Para una tabla de contingencia 4 $\times$ 2 como en este problema, hay 3 grados de libertad porque (4-1) (2-1) = 3 grados de libertad.

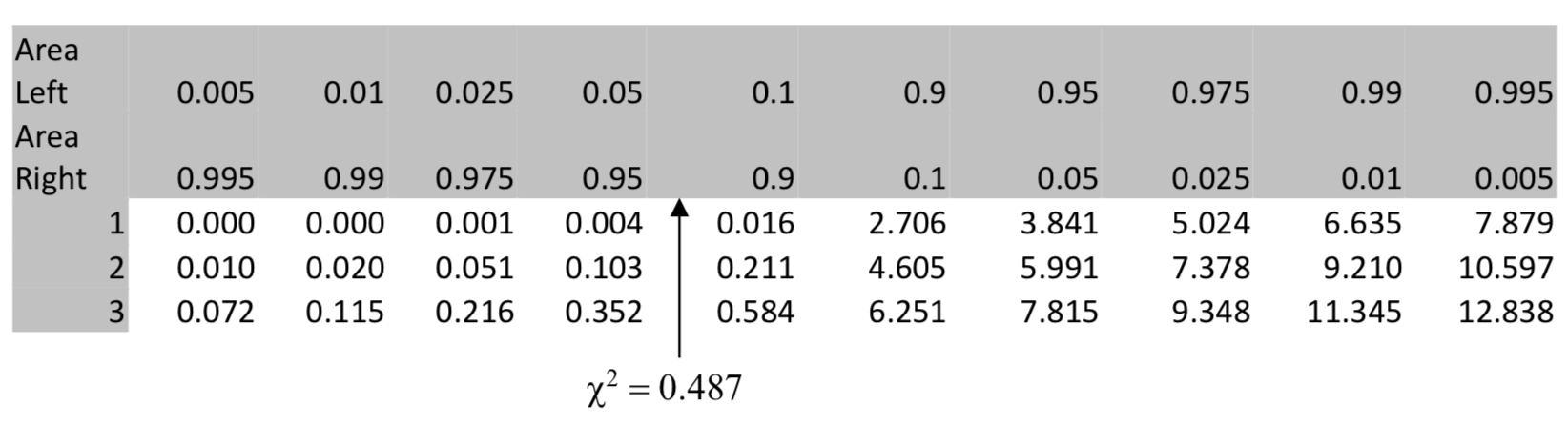
2019-05-17 3.00.37.png

En la tabla se muestra que el valor p es menor a 0.05. La calculadora confirma esto porque $\chi^2$ cdf (0.486, 1E99, 3) = 0.9218. En consecuencia, la conclusión es que no existe una diferencia significativa entre la distribución de huracanes en 1951-2000 y 1901-50.

Distinguir entre el uso de la prueba de independencia y homogeneidad

Si bien las matemáticas detrás tanto de la prueba de independencia como de la prueba de homogeneidad son las mismas, la intención detrás de su uso e interpretación de los resultados es diferente.

La prueba de independencia se utiliza cuando se determinan dos variables aleatorias, ambas consideradas como variables de respuesta, para cada unidad. La prueba de homogeneidad se utiliza cuando una de las variables aleatorias es la variable explicativa y los sujetos son seleccionados en función de su nivel de esta variable. La otra variable aleatoria es la variable de respuesta.

La determinación de qué prueba a utilizar se establece mediante el enfoque de muestreo. Si se definen claramente dos poblaciones de antemano y se realiza una selección aleatoria de cada población, entonces las poblaciones se compararán utilizando la prueba de homogeneidad. Si no se hace ningún esfuerzo para distinguir poblaciones de antemano, y se hace una selección aleatoria de esta población y luego se determinan los valores de las dos variables aleatorias, la prueba de independencia es apropiada.

Un ejemplo puede aclarar la sutil diferencia entre las dos pruebas. Considera que una variable aleatoria es la preferencia de una persona entre correr y nadar para hacer ejercicio y la otra variable aleatoria es la preferencia de una persona entre ver televisión o leer un libro. Si el investigador selecciona al azar a algunos corredores y algunos nadadores y pregunta a cada grupo sobre su preferencia por la televisión o leer un libro, la prueba de homogeneidad sería apropiada. Por otro lado, si el investigador encuestó a personas al azar y pregunta si prefieren correr o nadar y si prefieren la televisión o la lectura, entonces el objetivo será determinar si existe una correlación entre estas dos variables aleatorias mediante el uso de la prueba de independencia.

Distribuciones Chi Cuadradas
Área Izquierda	0.005	0.01	0.025	0.05	0.1	0.9	0.95	0.975	0.99	0.995
Área Derecha	0.995	0.99	0.975	0.95	0.9	0.1	0.05	0.025	0.01	0.005
df
1	0.000	0.000	0.001	0.004	0.016	2.706	3.841	5.024	6.635	7.879
2	0.010	0.020	0.051	0.103	0.211	4.605	5.991	7.378	9.210	10.597
3	0.072	0.115	0.216	0.352	0.584	6.251	7.815	9.348	11.345	12.838
4	0.207	0.287	0.484	0.711	1.064	7.779	9.488	11.143	13.277	14.860
5	0.412	0.554	0.831	1.145	1.610	9.236	11.070	12.832	15.086	16.750
6	0.676	0.872	1.237	1.635	2.204	10.645	12.592	14.449	16.812	18.548
7	0.989	1.239	1.690	2.167	2.833	12.017	14.067	16.013	18.475	20.278
8	1.344	1.647	2.180	2.733	3,490	13.362	15.507	17.535	20.090	21.955
9	1.735	2.088	2.700	3.325	4.168	14.684	16.919	19.023	21.666	23.589
10	2.156	2.558	3.247	3.940	4.865	15.987	18.307	20.483	23.209	25.188
11	2.603	3.053	3.816	4.575	5.578	17.275	19.675	21.920	24.725	26.757
12	3.074	3.571	4.404	5.226	6.304	18.549	21.026	23.337	26.217	28.300
13	3.565	4.107	5.009	5.892	7.041	19.812	22.362	24.736	27.688	29.819
14	4.075	4.660	5.629	6.571	7.790	21/064	23.685	26.119	29.141	31.319
15	4.601	5.229	6.262	7.261	8.547	22.307	24.996	27.488	30.578	32.801
16	5.142	5,812	6.908	7.962	9.312	23.542	26.296	28.845	32.000	34.267
17	5.697	6.408	7.564	8.672	10.085	24.769	27.587	30.191	33.409	35.718
18	6.265	7.015	8.231	9.390	10.865	25.989	28.869	31.526	34.805	37.156
19	6.844	7.633	8.907	10.117	11.651	27.204	30.144	32.852	36.191	38.582
20	7.434	8.260	9.591	10.851	12.443	28.412	31.410	34.170	37.566	39.997
21	8.034	8.897	10.283	11.591	13.240	29.615	32.671	35.479	38.932	41.401
22	8.643	9.542	10.982	12.338	14.041	30.813	33.924	36.781	40.289	42.796
23	9.260	10.196	11.689	13.091	14.848	32.007	35.172	38.076	41.638	44.181
24	9.886	10.856	12.401	13.848	15.659	33.196	36.415	39.365	42.980	45.558
25	10.520	11.524	13.120	14.611	16.473	34.382	37.652	40.646	44.314	46.928
26	11.160	12.198	13.844	15.379	17.292	35.563	38.885	41.923	45.642	48.290
27	11.808	12.878	14.573	16.151	18.114	36.741	40.113	43.195	46.963	49.645
28	12.461	13.565	15.398	16.928	18.939	37.916	41.337	44.461	48.278	50.994
29	13.121	14.256	16.047	17.708	19.768	39.087	42.557	45.722	49.588	52.335
30	13.787	14.953	16.791	18.493	20.599	40.256	43.773	46.979	50.892	53.672
40	20.707	22.164	24.433	26.509	29.051	51.805	55.758	59.342	63.691	66.766
50	27.991	29.707	32.357	34.764	37.689	63.167	67.505	71.420	76.154	79.490
60	35.534	37.485	40.482	43.188	46.459	74.397	79.082	83.298	88.379	91.952
70	43.275	45.442	48.758	51.739	55.329	85.527	90.531	95.023	100.425	104.215
80	51.172	53.540	57.153	60.391	64.278	96.578	101.879	106.629	112.329	116.321
90	59.196	61.754	65.647	69.126	73.291	107.565	113.145	118.136	124.116	128.299
100	67.328	70.065	74.222	77.929	82.358	118.498	124.342	129.561	135.807	140.170
110	75.550	78.458	82.867	86.792	91.471	129.385	135.480	140.916	147.414	151.948

Prueba de bondad de ajuste

Prueba de la Plaza Chi para la Independencia

Prueba de Chi Cuadrado para Homogeneidad

Support Center

How can we help?