1.3: ¿Qué pueden hacer las estadísticas por nosotros?

Hay tres cosas principales que podemos hacer con las estadísticas:

• Describir: El mundo es complejo y muchas veces necesitamos describirlo de una manera simplificada que podamos entender.
• Decidir: A menudo necesitamos tomar decisiones basadas en datos, generalmente ante la incertidumbre.
• Predecir: A menudo deseamos hacer predicciones sobre nuevas situaciones basadas en nuestro conocimiento de situaciones anteriores.

Veamos un ejemplo de estos en acción, centrado en una pregunta que a muchos de nosotros nos interesa: ¿Cómo decidimos qué es saludable comer?
Hay muchas fuentes diferentes de orientación, desde pautas dietéticas gubernamentales hasta libros de dieta y blogueros.
Centrémonos en una pregunta específica: ¿Las grasas saturadas en nuestra dieta son malas?

Una forma en que podríamos responder a esta pregunta es el sentido común.
Si comemos grasa entonces se va a convertir directamente en grasa en nuestros cuerpos, ¿verdad?
Y todos hemos visto fotos de arterias obstruidas con grasa, así que comer grasa va a obstruir nuestras arterias, ¿verdad?

Otra forma de responder a esta pregunta es escuchando figuras de autoridad. Las Guías Dietéticas de la Administración de Alimentos y Medicamentos de Estados Unidos tienen como una de sus Recomendaciones Clave que “Un patrón de alimentación saludable limita las grasas saturadas” .Se podría esperar que estas pautas se basen en la buena ciencia, y en algunos casos lo son, pero como Nina Teicholz esbozó en su libro “Big Fat Sorpresa” (Teicholz 2014), esta recomendación en particular parece estar basada más en el dogma de los investigadores de nutrición que en evidencia real.

Por último, podríamos mirar la investigación científica real. Empecemos por mirar un gran estudio llamado el estudio PURE, que ha examinado las dietas y los resultados de salud (incluida la muerte) en más de 135 mil personas de 18 países diferentes. En uno de los análisis de este conjunto de datos (publicado en The Lancet en 2017; Dehghan et al. (2017)), los investigadores de PURE reportaron un análisis de cómo la ingesta de diversas clases de macronutrientes (incluyendo grasas saturadas e hidratos de carbono) se relacionó con la probabilidad de morir durante el tiempo en que se siguió a la gente. Las personas fueron seguidas por una mediana de 7.4 años, lo que significa que la mitad de las personas en el estudio fueron seguidas por menos y la mitad fueron seguidas por más de 7.4 años. La Figura 1.1 traza algunos de los datos del estudio (extraídos del trabajo), mostrando la relación entre la ingesta tanto de grasas saturadas como de carbohidratos y el riesgo de morir por cualquier causa.

Figura 1.1: Gráfica de datos del estudio PURE, mostrando la relación entre la muerte por cualquier causa y la ingesta relativa de grasas saturadas e hidratos de carbono.

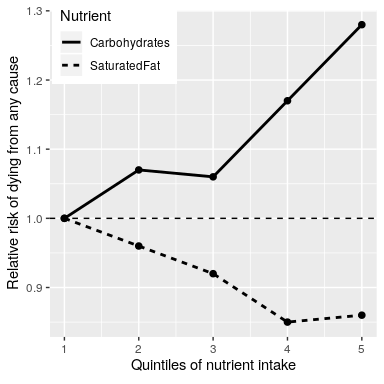
Esta trama se basa en diez números. Para obtener estos números, los investigadores dividieron el grupo de 135,335 participantes del estudio (que llamamos la “muestra”) en 5 grupos (“quintiles”) luego de ordenarlos en términos de su ingesta de cualquiera de los nutrientes; el primer quintil contiene el 20% de las personas con menor consumo, y el quinto quintil contiene el 20% con la ingesta más alta. Luego, los investigadores calcularon la frecuencia con la que las personas de cada uno de esos grupos morían durante el tiempo que estaban siendo seguidos. La cifra lo expresa en términos del riesgo relativo de morir en comparación con el quintil más bajo: Si este número es mayor a 1 significa que las personas del grupo tienen más probabilidades de morir que las personas del quintil más bajo, mientras que si es menor de uno significa que las personas en el grupo tiene menos probabilidades de morir. La cifra es bastante clara: Las personas que comían más grasas saturadas tuvieron menos probabilidades de morir durante el estudio, con la tasa de mortalidad más baja observada para las personas que estaban en el cuarto quintil (es decir, que comieron más grasa que el 60% más bajo pero menos que el 20% superior). Se observa lo contrario para los carbohidratos; cuantos más carbohidratos comió una persona, más probabilidades tenían de morir durante el estudio. Este ejemplo muestra cómo podemos usar estadísticas para describir un conjunto de datos complejo en términos de un conjunto de números mucho más simple; si tuviéramos que mirar los datos de cada uno de los participantes del estudio al mismo tiempo, estaríamos sobrecargados de datos y sería difícil ver el patrón que emerge cuando ellos se describen de manera más sencilla.

Los números en la Figura 1.1 parecen mostrar que las muertes disminuyen con las grasas saturadas y aumentan con la ingesta de carbohidratos, pero también sabemos que hay mucha incertidumbre en los datos; hay algunas personas que murieron temprano a pesar de que comieron una dieta baja en carbohidratos, y, de manera similar, algunas personas que comieron una tonelada de carbohidratos pero vivió hasta una vejez madura. Dada esta variabilidad, queremos decidir si las relaciones que vemos en los datos son lo suficientemente grandes como para que no esperemos que ocurran aleatoriamente si no hubiera realmente una relación entre la dieta y la longevidad. Las estadísticas nos proporcionan las herramientas para tomar este tipo de decisiones, y muchas veces la gente desde el exterior ve esto como el propósito principal de la estadística. Pero como veremos a lo largo del libro, esta necesidad de decisiones en blanco y negro basadas en evidencia borrosa a menudo ha llevado a los investigadores por mal camino.

Con base en los datos también nos gustaría hacer predicciones sobre resultados futuros. Por ejemplo, una compañía de seguros de vida podría querer usar datos sobre la ingesta de grasas y carbohidratos de una persona en particular para predecir cuánto tiempo es probable que viva. Un aspecto importante de la predicción es que nos obliga a generalizar desde los datos que ya tenemos a alguna otra situación, muchas veces en el futuro; si nuestras conclusiones se limitaran a las personas específicas del estudio en un momento determinado, entonces el estudio no sería muy útil. En general, los investigadores deben asumir que su muestra particular es representativa de una población mayor, lo que requiere que obtengan la muestra de una manera que proporcione una imagen imparcial de la población. Por ejemplo, si el estudio PURE hubiera reclutado a todos sus participantes de sectas religiosas que practican el vegetarianismo, entonces probablemente no quisiéramos generalizar los resultados a personas que siguen diferentes estándares dietéticos.