4.2: Resumir datos usando tablas

Una forma sencilla de resumir datos es generar una tabla que represente recuentos de diversos tipos de observaciones. Este tipo de mesa se ha utilizado desde hace miles de años (ver Figura 4.1).

Figura 4.1: Una tablilla sumeria del Louvre, que muestra un contrato de compraventa de una casa y campo. Dominio público, vía Wikimedia Commons.

Veamos algunos ejemplos del uso de tablas, nuevamente usando el conjunto de datos NHANES. Escriba el comando help (NHANES) en la consola de RStudio y desplácese por la página de ayuda, que debería abrirse dentro del panel de Ayuda si está utilizando RStudio. Esta página proporciona información sobre el conjunto de datos, así como una lista de todas las variables incluidas en el conjunto de datos. Echemos un vistazo a una variable simple, llamada “PhysActive” en el conjunto de datos. Esta variable contiene uno de tres valores diferentes: “Sí” o “No” (indicando si la persona reporta o no haber realizado “deportes, fitness o actividades recreativas de intensidad moderada o vigorosa”), o “NA” si faltan los datos para ese individuo. Existen diferentes razones por las que podrían faltar los datos; por ejemplo, esta pregunta no se hizo a niños menores de 12 años, mientras que en otros casos un adulto puede haber declinado responder a la pregunta durante la entrevista.

4.2.1 Distribuciones de frecuencia

Veamos cuántas personas entran en cada una de estas categorías. Lo haremos en R seleccionando la variable de interés (PhysActive) del conjunto de datos NHANES, agrupando los datos por los diferentes valores de la variable, y luego contando cuántos valores hay en cada grupo:

PhysActive	AbsoluteFrequency
No	2473
Sí	2972
NA	1334

Esta tabla muestra las frecuencias de cada uno de los diferentes valores; hubo 2473 individuos que respondieron “No” a la pregunta, 2972 quienes respondieron “Sí”, y 1334 para los que no se dio respuesta. A esto lo llamamos distribución de frecuencias porque nos dice qué tan frecuente es cada uno de los valores posibles dentro de nuestra muestra.

Esto nos muestra la frecuencia absoluta de las dos respuestas, para todos los que realmente dieron una respuesta. De esto podemos ver que hay más gente diciendo “Sí” que “No”, pero puede ser difícil distinguir por números absolutos qué tan grande es la diferencia. Por esta razón, a menudo preferiríamos presentar los datos usando frecuencia relativa, que se obtiene dividiendo cada frecuencia por la suma de todas las frecuencias:

\(\ relative frequency_{i}=\frac{\text {absolute frequency}_{i}}{\sum_{j=1}^{N} \text {absolute frequency}_{j}}\)

$$$$La frecuencia relativa proporciona una manera mucho más fácil de ver qué tan grande es el desequilibrio. También podemos interpretar las frecuencias relativas como porcentajes multiplicándolas por 100. En este ejemplo, también bajaremos los valores de NA, ya que nos gustaría poder interpretar las frecuencias relativas de personas activas versus inactivas.

Tabla 4.1: Frecuencias y porcentajes absolutos y relativos para la variable PhysActive

PhysActive	AbsoluteFrequency	RelativoRequency	Porcentaje
No	2473	0.45	45
Sí	2972	0.55	55

Esto nos permite ver que 45.4 por ciento de los individuos en la muestra de NHANES dijo “No” y 54.6 por ciento dijo “Sí”.

4.2.2 Distribuciones acumuladas

La variable PhysActive que examinamos anteriormente solo tenía dos valores posibles, pero a menudo deseamos resumir datos que pueden tener muchos más valores posibles. Cuando esos valores son cuantitativos, entonces una forma útil de resumirlos es a través de lo que llamamos una representación de frecuencia acumulativa: en lugar de preguntar cuántas observaciones toman un valor específico, preguntamos cuántas tienen un valor de al menos algún valor específico.

Veamos otra variable en el conjunto de datos de NHANES, llamada SleePhrsNight que registra cuántas horas informa el participante durmiendo los días de semana habituales. Vamos a crear una tabla de frecuencias como lo hicimos anteriormente, luego de eliminar a cualquiera que no diera respuesta a la pregunta.

Tabla 4.2: Distribución de frecuencia para el número de horas de sueño por noche en el conjunto de datos NHANES

SleePhrsNight	AbsoluteFrequency	RelativoRequency	Porcentaje
2	9	0.00	0.18
3	49	0.01	0.97
4	200	0.04	3.97
5	406	0.08	8.06
6	1172	0.23	23.28
7	1394	0.28	27.69
8	1405	0.28	27.90
9	271	0.05	5.38
10	97	0.02	1.93
11	15	0.00	0.30
12	17	0.00	0.34

Ya podemos comenzar a resumir el conjunto de datos con solo mirar la tabla; por ejemplo, podemos ver que la mayoría de las personas reportan dormir entre 6 y 8 horas. Trazemos los datos para ver esto con mayor claridad. Para ello podemos trazar un histograma que muestra el número de casos que tienen cada uno de los diferentes valores; ver panel izquierdo de la Figura 4.2. La biblioteca ggplot2 () tiene una función de histograma incorporada (geom_histogram ()) que usaremos a menudo. También podemos trazar las frecuencias relativas, a las que a menudo nos referiremos como densidades - ver el panel derecho de la Figura 4.2.

Figura 4.2: Izquierda: Histograma que muestra el número (izquierda) y la proporción (derecha) de personas que reportan cada valor posible de la variable SleePhrsNight.

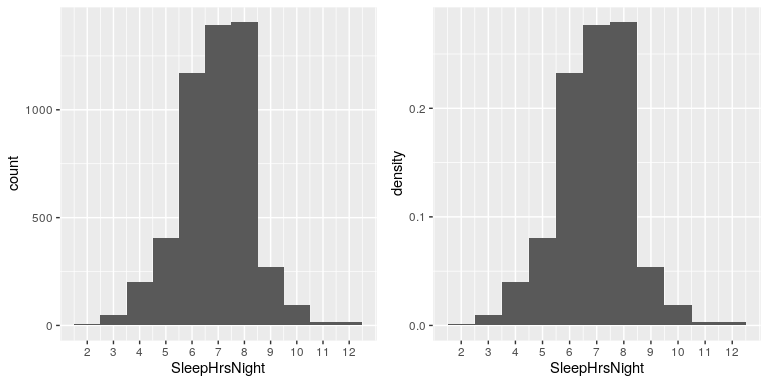
¿Y si queremos saber cuántas personas reportan dormir 5 horas o menos? Para encontrar esto, podemos calcular una distribución acumulativa. Para calcular la frecuencia acumulada para algún valor j, sumamos las frecuencias para todos los valores hasta e incluyendo j:

$$$$

frecuencia acumulativa frecuencia\(_{j}=\sum_{i=1}^{j}\) absoluta\(_{i}\)

Tabla 4.3: Distribuciones de frquencia absoluta y acumulativa para la variable SleePhrsNight

SleePhrsNight	AbsoluteFrequency	CumulativeRequency
2	9	9
3	49	58
4	200	258
5	406	664
6	1172	1836
7	1394	3230
8	1405	4635
9	271	4906
10	97	5003
11	15	5018
12	17	5035

En el panel izquierdo de la Figura 4.3 trazamos los datos para ver cómo se ven estas representaciones; los valores absolutos de frecuencia se trazan en líneas continuas, y las frecuencias acumulativas se trazan en líneas discontinuas Vemos que la frecuencia acumulativa está aumentando monótonamente —es decir, sólo puede subir o mantenerse constante, pero nunca puede disminuir. Nuevamente, generalmente encontramos que las frecuencias relativas son más útiles que las absolutas; esas se trazan en el panel derecho de la Figura 4.3.

Figura 4.3: Gráfica de los valores relativos (sólidos) y relativos acumulativos (discontinuos) para frecuencia (izquierda) y proporción (derecha) para los posibles valores de SleePhrsNight.

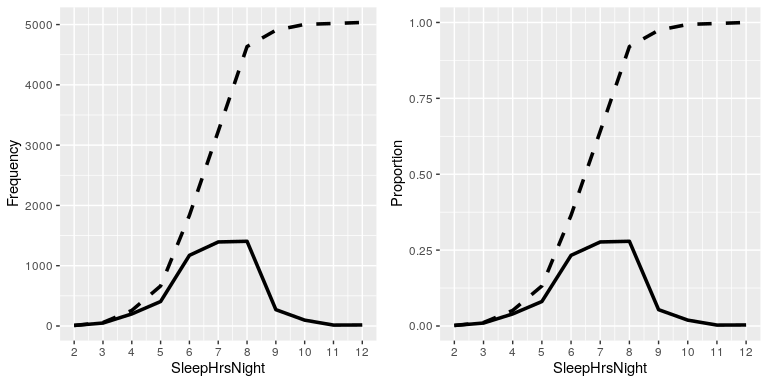
4.2.3 Trazado de histogramas

Figura 4.4: Histograma de las variables Edad (izquierda) y Altura (derecha) en NHANES.

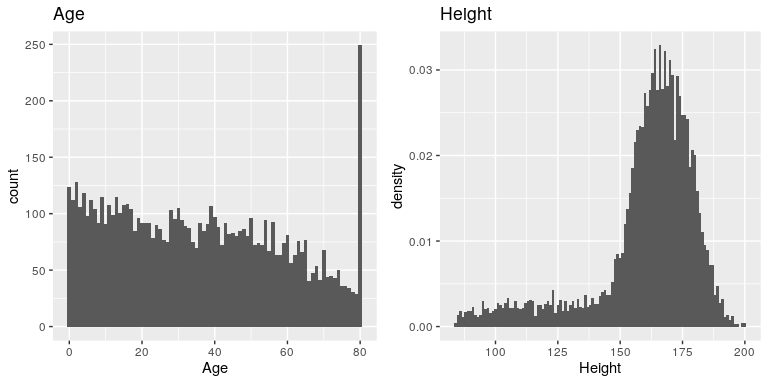
Las variables que examinamos anteriormente fueron bastante simples, teniendo sólo unos pocos valores posibles. Ahora veamos una variable más compleja: Edad. Primero trazemos la variable Edad para todos los individuos en el conjunto de datos NHANES (ver panel izquierdo de la Figura 4.4). ¿Qué ves ahí? Primero, debes notar que el número de individuos en cada grupo de edad está disminuyendo con el tiempo. Esto tiene sentido porque la población está siendo muestreada aleatoriamente, y así la muerte a lo largo del tiempo conduce a un menor número de personas en los rangos de edad mayores. Segundo, probablemente notes un gran pico en la gráfica a los 80 años. ¿De qué crees que se trata?

Si miras la función de ayuda para el conjunto de datos de NHANES, verás la siguiente definición: “Edad en años en el cribado del participante del estudio. Nota: Los sujetos de 80 años o más se registraron como 80”. La razón de esto es que el número relativamente pequeño de individuos con edades muy altas haría potencialmente más fácil identificar a la persona específica en el conjunto de datos si supiera su edad exacta; los investigadores generalmente prometen a sus participantes mantener su identidad confidencial, y esta es una de las cosas que pueden hacer para ayudar a proteger a sus sujetos de investigación. Esto también resalta el hecho de que siempre es importante saber de dónde provienen los datos y cómo se han procesado; de lo contrario podríamos interpretarlos indebidamente, pensando que los niños de 80 años habían estado de alguna manera sobrerrepresentados en la muestra.

Veamos otra variable más compleja en el conjunto de datos de NHANES: Altura. El histograma de valores de altura se traza en el panel derecho de la Figura 4.4. Lo primero que debes notar de esta distribución es que la mayor parte de su densidad se centra alrededor de unos 170 cm, pero la distribución tiene una “cola” a la izquierda; hay un pequeño número de individuos con alturas mucho menores. ¿Qué crees que está pasando aquí?

Es posible que haya intuido que las pequeñas alturas provienen de los hijos en el conjunto de datos. Una forma de examinar esto es graficar el histograma con colores separados para niños y adultos (panel izquierdo de la Figura 4.5). Esto demuestra que todas las alturas muy cortas en efecto provenían de niños de la muestra. Vamos a crear una nueva versión de NHANES que solo incluya adultos, y luego trazar el histograma solo para ellos (panel derecho de la Figura 4.5). En esa trama que la distribución se ve mucho más simétrica. Como veremos más adelante, este es un buen ejemplo de una distribución normal (o gaussiana).

Figura 4.5: Histograma de alturas para NHANES. A: valores trazados por separado para niños (gris) y adultos (negro). B: valores sólo para adultos. C: Igual que B, pero con ancho de contenedor = 0.1

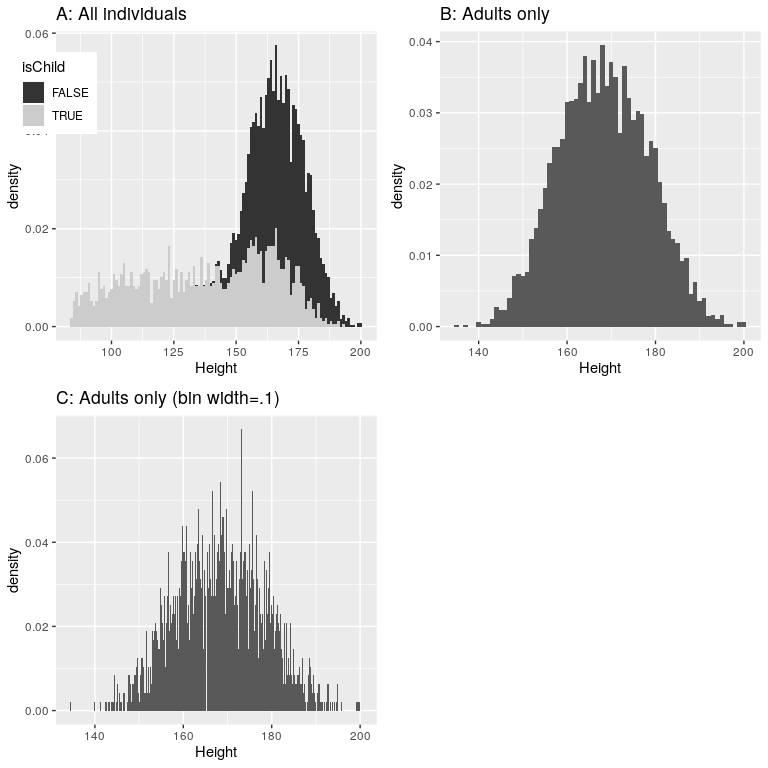
4.2.4 Contenedores de histograma

En nuestro ejemplo anterior con la variable sueño, los datos fueron reportados en números enteros, y simplemente contamos el número de personas que reportaron cada valor posible. No obstante, si observas algunos valores de la variable Altura en NHANES, verás que se midió en centímetros hasta el primer decimal:

Cuadro 4.4: Algunos valores del marco de datos NHANES.

Altura
170
170
168
155
174
174

El Panel C de la Figura 4.5 muestra un histograma que cuenta la densidad de cada valor posible. Ese histograma se ve realmente dentado, lo que se debe a la variabilidad en valores decimales específicos. Por ejemplo, el valor 173.2 ocurre 32 veces, mientras que el valor 173.3 solo ocurre 15 veces. Probablemente no pensemos que realmente haya una diferencia tan grande entre la prevalencia de estos dos pesos; más probablemente esto se deba solo a la variabilidad aleatoria en nuestra muestra de personas.

En general, cuando creamos un histograma de datos que son continuos o donde hay muchos valores posibles, ubicaremos los valores para que en lugar de contar y trazar la frecuencia de cada valor específico, contemos y trazemos la frecuencia de valores que caen dentro de un rango específico. Es por eso que la gráfica se veía menos dentada arriba en el Panel B de 4.5; en este panel establecemos el ancho de bin en 1, lo que significa que el histograma está calculando combinando valores dentro de bins con un ancho de uno; así, los valores 1.3, 1.5 y 1.6 contarían todos hacia la frecuencia del mismo bin, que abarcaría desde valores iguales a uno hacia arriba a través de valores menores a 2.

Tenga en cuenta que una vez que se ha seleccionado el tamaño de bin, entonces el número de bins es determinado por los datos:$$$$

número de contenedores\(=\frac{\text { range of scores }}{\text { bin width }}\)

No existe una regla dura y rápida sobre cómo elegir el ancho óptimo de la papelera. Ocasionalmente será obvio (como cuando solo hay unos pocos valores posibles), pero en muchos casos requeriría ensayo y error. Existen métodos que intentan encontrar automáticamente un tamaño de bin óptimo, como el método Freedman-Diaconis (que se implementa dentro de la función nClass.fd () en R); utilizaremos esta función en algunos ejemplos posteriores.