4.3: Representaciones idealizadas de distribuciones

Los conjuntos de datos son como copos de nieve, en que cada uno es diferente, pero sin embargo hay patrones que a menudo se ven en diferentes tipos de datos. Esto nos permite utilizar representaciones idealizadas de los datos para resumirlos aún más. Tomemos los datos de estatura del adulto trazados en 4.5, y trazémoslos junto a una variable muy diferente: la frecuencia del pulso (latidos por minuto), también medidos en NHANES (ver Figura 4.6).

Figura 4.6: Histogramas para altura (izquierda) y pulso (derecha) en el conjunto de datos NHANES, con la distribución normal superpuesta para cada conjunto de datos.

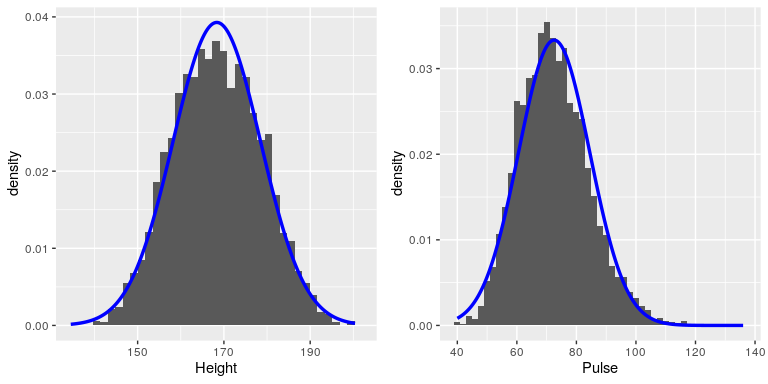
Si bien estas parcelas ciertamente no se ven exactamente iguales, ambas tienen la característica general de ser relativamente simétricas alrededor de un pico redondeado en el medio. Esta forma es, de hecho, una de las formas de distribución comúnmente observadas cuando recopilamos datos, a los que llamamos distribución normal (o gaussiana). Esta distribución se define en términos de dos valores (a los que llamamos parámetros de la distribución): la ubicación del pico central (que llamamos la media) y el ancho de la distribución (que se describe en términos de un parámetro llamado desviación estándar). La Figura 4.6 muestra la distribución normal apropiada trazada encima de cada uno de los histrogramas.Se puede ver que aunque las curvas no se ajustan exactamente a los datos, hacen un trabajo bastante bueno al caracterizar la distribución, ¡con solo dos números!

Como veremos más adelante en el curso cuando discutamos el teorema del límite central, hay una profunda razón matemática por la cual muchas variables en el mundo exhiben la forma de una distribución normal.

4.3.1 Asimetría

Los ejemplos de la Figura 4.6 siguieron bastante bien la distribución normal, pero en muchos casos los datos se desviarán de manera sistemática de la distribución normal. Una forma en la que los datos pueden desviarse es cuando son asimétricos, de tal manera que una cola de la distribución es más densa que la otra. Nos referimos a esto como “asimetría”. La asimetría ocurre comúnmente cuando la medición está restringida a no ser negativa, como cuando estamos contando cosas o midiendo los tiempos transcurridos (y así la variable no puede tomar valores negativos).

Un ejemplo de asimetría se puede ver en los tiempos de espera promedio en las líneas de seguridad aeroportuaria del Aeropuerto Internacional de San Francisco, trazados en el panel izquierdo de la Figura 4.7. Se puede ver que si bien la mayoría de los tiempos de espera son menores a 20 minutos, hay una serie de casos en los que son mucho más largos, ¡más de 60 minutos! Este es un ejemplo de una distribución “sesgada a la derecha”, donde la cola derecha es más larga que la izquierda; estos son comunes al mirar recuentos o tiempos medidos, que no pueden ser menores que cero. Es menos común ver distribuciones “sesgadas a la izquierda”, pero pueden ocurrir, por ejemplo al mirar valores fraccionarios que no pueden tomar un valor mayor que uno.

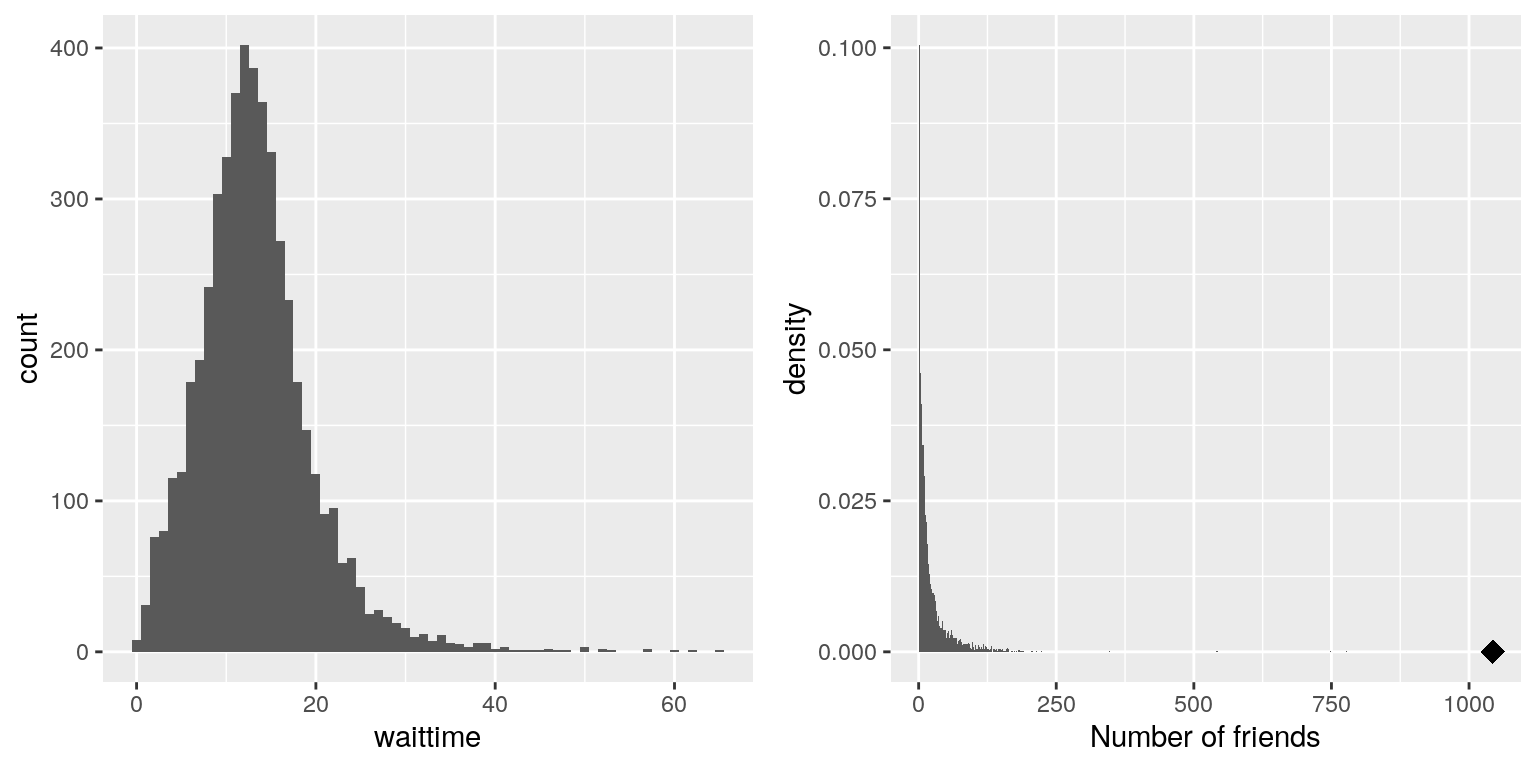
Figura 4.7: Ejemplos de distribuciones sesgadas a la derecha y de cola larga. Izquierda: Promedio de tiempos de espera para la seguridad en SFO Terminal A (Ene-Oct 2017), obtenidos de https://awt.cbp.gov/. Derecha: Histograma del número de amigos de Facebook entre 3,663 individuos, obtenido de la Base de Datos de la Red Grande de Stanford. La persona con el número máximo de amigos es indicada por el diamante.

4.3.2 Distribuciones de cola larga

Históricamente, las estadísticas se han centrado mucho en los datos que normalmente se distribuyen, pero hay muchos tipos de datos que no se parecen en nada a la distribución normal. En particular, muchas distribuciones del mundo real son “de cola larga”, lo que significa que la cola derecha se extiende mucho más allá de los miembros más típicos de la distribución. Uno de los tipos de datos más interesantes donde ocurren distribuciones de cola larga surge del análisis de las redes sociales. Por ejemplo, veamos los datos de amigos de Facebook de la base de datos de Stanford Large Network y trazemos el histograma del número de amigos a través de las 3,663 personas en la base de datos (ver panel derecho de la Figura 4.7). Como podemos ver, esta distribución tiene una cola derecha muy larga — la persona promedio tiene 24.09 amigos, mientras que la persona con más amigos (denotada por el punto azul) tiene 1043!

Las distribuciones de cola larga son cada vez más reconocidas en el mundo real. En particular, muchas características de sistemas complejos se caracterizan por estas distribuciones, desde la frecuencia de las palabras en el texto, hasta el número de vuelos dentro y fuera de diferentes aeropuertos, hasta la conectividad de las redes cerebrales. Hay varias formas diferentes en las que pueden producirse distribuciones de cola larga, pero una común ocurre en los casos del llamado “efecto Mateo” de la Biblia cristiana:

Porque a cada quien tiene se le dará más, y tendrá abundancia; pero del que no tiene, incluso lo que tiene le será quitado. — Mateo 25:29, Versión Estándar Revisada

Esto suele parafrasearse como “los ricos se hacen más ricos”. En estas situaciones, las ventajas se suman, de tal manera que quienes tienen más amigos tienen acceso a aún más nuevos amigos, y los que tienen más dinero tienen la capacidad de hacer cosas que incrementan aún más sus riquezas.

A medida que avance el curso veremos varios ejemplos de distribuciones de cola larga, y debemos tener en cuenta que muchas de las herramientas en estadística pueden fallar cuando se enfrentan a datos de cola larga. Como señaló Nassim Nicholas Taleb en su libro “El cisne negro”, tales distribuciones de cola larga jugaron un papel crítico en la crisis financiera de 2008, debido a que muchos de los modelos financieros utilizados por los comerciantes asumieron que los sistemas financieros seguirían la distribución normal, lo que claramente no lo hicieron.