14.3: Generando Números Aleatorios

Última actualización
Guardar como PDF

Page ID: 150567

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ejecutar una simulación de Monte Carlo requiere que generemos números aleatorios. Generar números verdaderamente aleatorios (es decir, números que son completamente impredecibles) solo es posible a través de procesos físicos, como la descomposición de los átomos o el tirado de dados, que son difíciles de obtener y/o demasiado lentos para ser útiles para la simulación por computadora (aunque se pueden obtener del NIST Aleatoriedad Baliza).

En general, en lugar de números verdaderamente aleatorios utilizamos números pseudo-aleatorios generados usando un algoritmo informático; estos números parecerán aleatorios en el sentido de que son difíciles de predecir, pero la serie de números en realidad se repetirá en algún momento. Por ejemplo, el generador de números aleatorios utilizado en R se repetirá después $2^ {19937} - 1$ números. Eso es mucho más que el número de segundos en la historia del universo, y generalmente pensamos que esto está bien para la mayoría de los propósitos en el análisis estadístico.

En R, existe una función para generar números aleatorios para cada una de las principales distribuciones de probabilidad, tales como:

runif () - distribución uniforme (todos los valores entre 0 y 1 por igual)
rnorm () - distribución normal
rbinom () - distribución binomial (por ejemplo, rodar los dados, voltear monedas)

La Figura 14.1 muestra ejemplos de números generados usando las funciones runif () y rnorm (), generados usando el siguiente código:

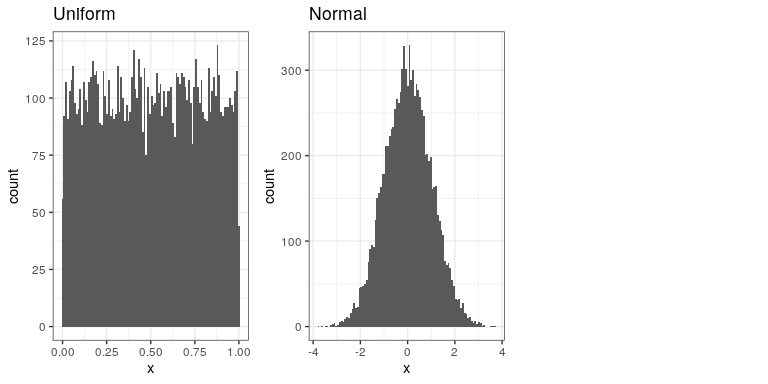
Figura 14.1: Ejemplos de números aleatorios generados a partir de una distribución uniforme (izquierda) o normal (derecha).

También puede generar números aleatorios para cualquier distribución si tiene una función cuantil para la distribución. Esta es la inversa de la función de distribución acumulativa; en lugar de identificar las probabilidades acumulativas para un conjunto de valores, la función cuantil identifica los valores para un conjunto de probabilidades acumulativas. Usando la función quantile, podemos generar números aleatorios a partir de una distribución uniforme, y luego mapearlos en la distribución de interés a través de su función quantile.

Por defecto, R generará un conjunto diferente de números aleatorios cada vez que ejecute una de las funciones generadoras de números aleatorios descritas anteriormente. Sin embargo, también es posible generar exactamente el mismo conjunto de números aleatorios, estableciendo lo que se llama la semilla aleatoria a un valor específico. Esto lo haremos en muchos de los ejemplos de este libro, para asegurarnos de que los ejemplos sean reproducibles.

Si ejecutamos la función rnorm () dos veces, nos dará diferentes conjuntos de números pseudoaleatorios cada vez:

print(rnorm(n = 5))

## [1]  1.48  0.18  0.21 -0.15 -1.72

print(rnorm(n = 5))

## [1] -0.691 -2.231  0.391  0.029 -0.647

Sin embargo, si establecemos la semilla aleatoria en el mismo valor cada vez usando la función set.seed (), entonces nos dará la misma serie de números pseudoaleatorios cada vez:

set.seed(12345)
print(rnorm(n = 5))

## [1]  0.59  0.71 -0.11 -0.45  0.61

set.seed(12345)
print(rnorm(n = 5))

## [1]  0.59  0.71 -0.11 -0.45  0.61