20.4: Estimación de distribuciones posteriores

En el ejemplo anterior solo había dos resultados posibles —el explosivo está ahí o no— y queríamos saber cuál resultado probablemente fue dado los datos. Sin embargo, en otros casos queremos utilizar la estimación bayesiana para estimar el valor numérico de un parámetro. Digamos que queremos saber sobre la efectividad de un nuevo medicamento para el dolor; para probarlo, podemos administrar el medicamento a un grupo de pacientes y luego preguntarles si su dolor mejoró o no después de tomar el medicamento. Podemos utilizar el análisis bayesiano para estimar la proporción de personas para las que el medicamento será efectivo utilizando estos datos.

20.4.1 Especificar el

TBD: MH: ¿UTILIZAR PREVIO PRECIOSO

En este caso, no tenemos ninguna información previa sobre la efectividad del medicamento, por lo que usaremos una distribución uniforme como nuestra anterior, ya que todos los valores son igualmente probables bajo una distribución uniforme. Para simplificar el ejemplo, solo veremos un subconjunto de 99 valores posibles de efectividad (de .01 a .99, en pasos de .01). Por lo tanto, cada valor posible tiene una probabilidad previa de 1/99.

20.4.2 Recopilar algunos datos

Necesitamos algunos datos para estimar el efecto del medicamento. Digamos que administramos el medicamento a 100 individuos, encontramos que 64 responden positivamente al medicamento.

20.4.3 Cálculo de la probabilidad

Podemos calcular la probabilidad de los datos bajo cualquier valor particular del parámetro de efectividad usando la función dbinom () en R. En la Figura 20.2 se pueden ver las curvas de verosimilitud sobre números de respondedores para varios valores diferentes de$P$. Mirando esto, parece que nuestros datos observados son relativamente más probables bajo la hipótesis de$P_ {responder} =0.7$, algo menos probable bajo la hipótesis de$P_ {responder} =0.5$, y bastante improbable bajo la hipótesis de$P_ {responder} =0.3$. Una de las ideas fundamentales de la inferencia bayesiana es que debemos elevar nuestra creencia en los valores de nuestro parámetro de interés en proporción a la probabilidad de que estén los datos por debajo de esos valores, equilibrados con lo que creemos sobre los valores de los parámetros antes de haber visto los datos (nuestro conocimiento previo).

Figura 20.2: Probabilidad de cada posible número de respondedores bajo varias hipótesis diferentes (p (responder) =0.5 (sólido), 0.7 (punteado), 0.3 (discontinua). El valor observado se muestra en la línea vertical

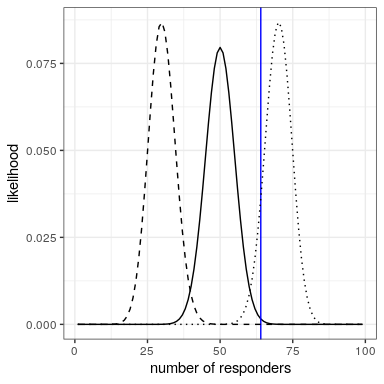
20.4.4 Computación de la probabilidad marginal

Además de la probabilidad de los datos bajo diferentes hipótesis, necesitamos conocer la probabilidad general de los datos, combinando todas las hipótesis (es decir, la probabilidad marginal). Esta probabilidad marginal es principalmente importante porque ayuda a asegurar que los valores posteriores sean verdaderas probabilidades. En este caso, nuestro uso de un conjunto de valores discretos de parámetros posibles facilita el cálculo de la probabilidad marginal, ya que podemos simplemente calcular la probabilidad de cada valor de parámetro bajo cada hipótesis y sumarlos.

MH: no estoy seguro de que haya habido una discusión clara de la probabilidad marginal hasta este punto. es un constructo confuso y también muy profundo.. la probabilidad general de los datos es la probabilidad de los datos bajo cada hipótesis, promediada togeteher (weifhted por) la probabilidad previa de esas hipótesis. es la probabilidad de que los datos estén bajo sus creencias previas sobre las hipótesis.

podría valer la pena pensar en dos ejemplos, donde la probabilidad de los datos bajo la hipótesis de interés es la misma, pero donde la probabilidad marginal cambia es decir, la hipótesis es bastante buena para predecir los datos, mientras que otras hipótesis son malas vs. otras hipótesis siempre son buenas (quizás mejor)

20.4.5 Computación de la parte posterior

Ahora tenemos todas las partes que necesitamos para calcular la distribución de probabilidad posterior a través de todos los valores posibles de$p_{respond}$

Figura 20.3: Distribución de probabilidad posterior para los datos observados trazados en línea continua contra distribución previa uniforme (línea punteada). El valor máximo a posteriori (MAP) está representado por el símbolo de diamante.

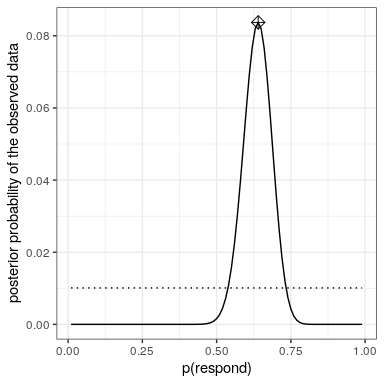
20.4.6 Estimación máxima a posteriori (MAP)

Dados nuestros datos nos gustaría obtener una estimación de$p_{respond}$

20.4.7 Intervalos creíbles

Muchas veces nos gustaría saber no solo una estimación para la posterior, sino un intervalo en el que estamos seguros de que la posterior cae. Anteriormente discutimos el concepto de intervalos de confianza en el contexto de la inferencia frecuentista, y tal vez recuerdes que la interpretación de los intervalos de confianza fue particularmente enrevesada: Fue un intervalo que contendrá el valor del parámetro 95% del tiempo. Lo que realmente queremos es un intervalo en el que estemos seguros de que el verdadero parámetro cae, y las estadísticas bayesianas nos pueden dar tal intervalo, que llamamos intervalo creíble.

TBD: UTILIZAR CORRESPONDIENTE

La interpretación de este intervalo creíble está mucho más cerca de lo que habíamos esperado que pudiéramos obtener de un intervalo de confianza (pero no pudimos): Nos dice que hay un 95% de probabilidad de que el valor de$p$cae entre estos dos valores. Es importante destacar que demuestra que tenemos alta confianza en que$p_ {respond} > 0.0$, lo que significa que la droga parece tener un efecto positivo.

En algunos casos el intervalo creíble puede calcularse numéricamente con base en una distribución conocida, pero es más común generar un intervalo creíble por muestreo a partir de la distribución posterior y luego calcular cuantiles de las muestras. Esto resulta particularmente útil cuando no tenemos una manera fácil de expresar numéricamente la distribución posterior, lo que suele ser el caso en el análisis real de datos bayesianos. Uno de esos métodos (muestreo de rechazo) se explica con más detalle en el Apéndice al final de este capítulo.

20.4.8 Efectos de diferentes antecedentes

En el ejemplo anterior usamos un prior plano, lo que significa que no teníamos ninguna razón para creer que ningún valor particular de$p$era más o menos probable. No obstante, digamos que en cambio habíamos comenzado con algunos datos previos: En un estudio anterior, los investigadores habían probado a 20 personas y encontraron que 10 de ellas habían respondido positivamente. Esto nos habría llevado a comenzar con una creencia previa de que el tratamiento tiene un efecto en el 50% de las personas. Podemos hacer el mismo cálculo que el anterior, pero utilizando la información de nuestro estudio anterior para informar a nuestro anterior (ver oanel A en la Figura 20.4).

MH: me pregunto qué estás haciendo aquí: ¿es esto lo mismo que hacer una inferencia bayesiana asumiendo 10/20 datos y usando el posterior de eso como el previo para este análisis? eso es lo que normalmente sería lo directo que hay que hacer.

Obsérvese que la verosimilitud y probabilidad marginal no cambiaron, solo la previa cambió. El efecto del cambio en el previo a fue acercar la parte posterior a la masa del nuevo previo, la cual se centra en 0.5.

Ahora veamos qué pasa si llegamos al análisis con una creencia previa aún más fuerte. Digamos que en lugar de haber observado previamente a 10 respondedores de 20 personas, el estudio anterior había probado a 500 personas y había encontrado a 250 respondedores. Esto debería en principio darnos un previo mucho más fuerte, y como vemos en el panel B de la Figura 20.4, eso es lo que sucede: El previo está mucho más concentrado alrededor de 0.5, y el posterior también está mucho más cerca del anterior. La idea general es que la inferencia bayesiana combina la información del previo y la verosimilitud, ponderando la fuerza relativa de cada uno.

Este ejemplo también destaca la naturaleza secuencial del análisis bayesiano: el posterior de un análisis puede convertirse en el previo para el siguiente análisis.

Por último, es importante darse cuenta de que si los antecedentes son lo suficientemente fuertes, pueden abrumar por completo los datos. Digamos que tienes un previo absoluto que$p$es 0.8 o mayor, de tal manera que establece la probabilidad previa de todos los demás valores en cero. ¿Qué pasa si luego calculamos el posterior?

Figura 20.4: A: Efectos de los antecedentes sobre la distribución posterior. La distribución posterior original basada en un previo plano se grafica en azul. El previo basado en la observación de 10 respondedores de 20 personas se traza en la línea punteada negra, y el posterior usando este previo se grafica en rojo. B: Efectos de la fuerza del prior sobre la distribución posterior. La línea azul muestra el posterior obtenido utilizando el previo basado en 50 cabezas de cada 100 personas. La línea negra punteada muestra el previo basado en 250 cabezas de 500 volteretas, y la línea roja muestra la posterior basada en esa previa. C: Efectos de la fuerza del prior sobre la distribución posterior. La línea azul muestra la posterior obtenida utilizando un previo absoluto que establece que p (responder) es 0.8 o mayor. El previo se muestra en la línea punteada negra.

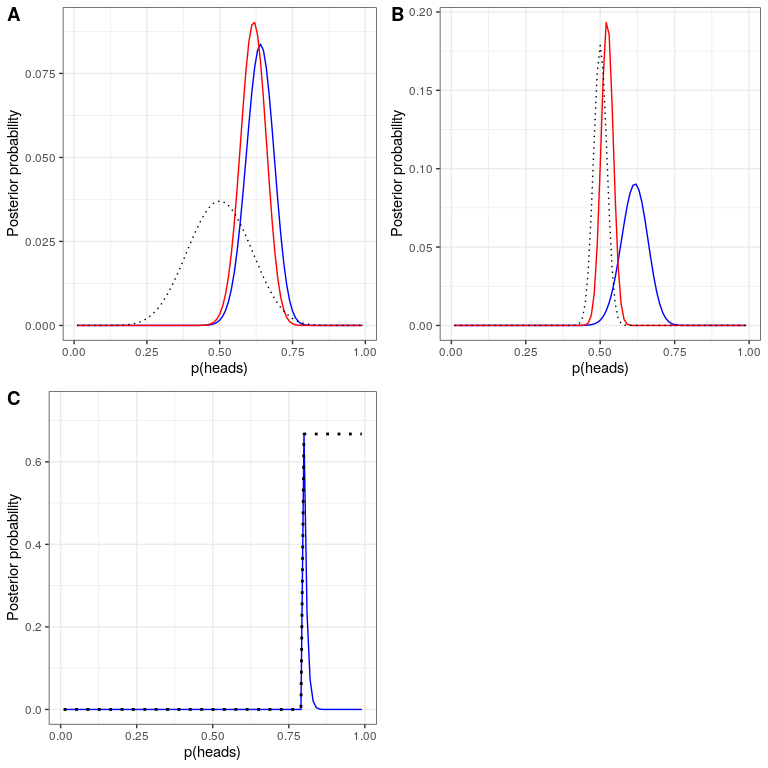
En el panel C de la Figura 20.4 vemos que hay densidad cero en la parte posterior para cualquiera de los valores donde el anterior se fijó en cero - los datos son abrumados por el previo absoluto.