28.5: Comparación de observaciones pareadas

Última actualización
Guardar como PDF

Page ID: 150525

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

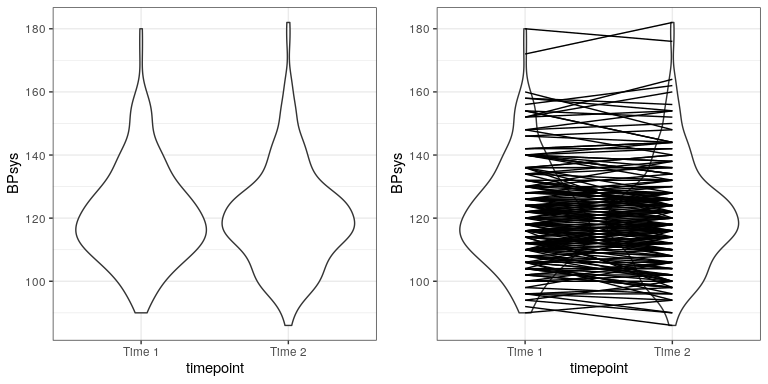
Izquierda: Parcela violín de presión arterial sistólica en primera y segunda grabación, de NHANES. Derecha: Misma trama de violín con líneas que conectan los dos puntos de datos para cada individuo. — Figura 28.2: Izquierda: Gráfica violín de presión arterial sistólica en primer y segundo registro, de NHANES. Derecha: Misma trama de violín con líneas que conectan los dos puntos de datos para cada individuo.

En la investigación experimental, a menudo utilizamos diseños dentro de sujetos, en los que comparamos a una misma persona en múltiples mediciones. Las medidas que provienen de este tipo de diseño a menudo se denominan medidas repetidas. Por ejemplo, en el conjunto de datos NHANES se midió la presión arterial tres veces. Digamos que nos interesa probar si existe una diferencia en la presión arterial media entre la primera y la segunda medición (Figura 28.2). Vemos que no parece haber mucha diferencia en la presión arterial media entre puntos de tiempo (aproximadamente un punto). Primero probemos una diferencia usando una prueba t de muestras independientes, que ignora el hecho de que pares de puntos de datos provienen de los mismos individuos.

## 
##  Two Sample t-test
## 
## data:  BPsys by timepoint
## t = 0.6, df = 398, p-value = 0.5
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -2.1  4.1
## sample estimates:
## mean in group BPSys1 mean in group BPSys2 
##                  121                  120

Este análisis no muestra diferencias significativas. Sin embargo, este análisis es inapropiado ya que asume que las dos muestras son independientes, cuando en realidad no lo son, ya que los datos provienen de los mismos individuos. Podemos trazar los datos con una línea para cada individuo para mostrar esto (ver Figura?? ).

En este análisis, lo que realmente nos importa es si la presión arterial de cada persona cambió de manera sistemática entre las dos mediciones, así que otra forma de representar los datos es computar la diferencia entre los dos puntos de tiempo para cada individuo, y luego analizar estas puntuaciones de diferencia en lugar de analizar las mediciones individuales. En la Figura 28.3, se muestra un histograma de estas puntuaciones de diferencia, con una línea azul que denota la diferencia media.

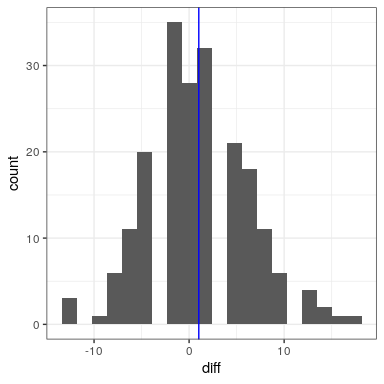
Figura 28.3: Histograma de puntuaciones de diferencia entre la primera y la segunda medición de PA. La línea vertical representa la diferencia media en la muestra.

28.5.1 Prueba de signos

Una forma sencilla de probar las diferencias es usar la prueba de signos. Para ello, tomamos las diferencias y calculamos su signo, y luego usamos una prueba binomial para preguntar si la proporción de signos positivos difiere de 0.5.

## 
##  Exact binomial test
## 
## data:  npos and nrow(NHANES_sample)
## number of successes = 96, number of trials = 200, p-value = 0.6
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
##  0.41 0.55
## sample estimates:
## probability of success 
##                   0.48

Aquí vemos que la proporción de individuos con signos positivos (0.48) no es lo suficientemente grande como para ser sorprendente bajo la hipótesis nula de $p=0.5$ . Sin embargo, un problema con la prueba de signos es que está desechando información sobre la magnitud de las diferencias, y así podría estar faltando algo.

28.5.2 Prueba t pareada

Una estrategia más común es usar una prueba t pareada, que equivale a una prueba t de una muestra para determinar si la diferencia media entre las mediciones es cero. Podemos calcular esto usando la función t.test () en R y estableciendo paired=true.

## 
##  Paired t-test
## 
## data:  BPsys by timepoint
## t = 3, df = 199, p-value = 0.007
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  0.29 1.75
## sample estimates:
## mean of the differences 
##                       1

Con estos análisis vemos que de hecho existe una diferencia significativa entre las dos mediciones. Calculemos el factor Bayes para ver cuánta evidencia aporta el resultado:

## Bayes factor analysis
## --------------
## [1] Alt., r=0.707 : 3 ±0%
## 
## Against denominator:
##   Null, mu = 0 
## ---
## Bayes factor type: BFoneSample, JZS

Esto nos muestra que aunque el efecto fue significativo en una prueba t pareada, en realidad aporta muy poca evidencia a favor de la hipótesis alternativa.

La prueba t pareada también se puede definir en términos de un modelo lineal; consulte el Apéndice para más detalles al respecto.