28.6: Comparando más de dos medias

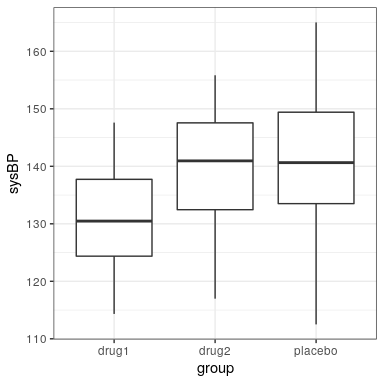
A menudo queremos comparar más de dos medias para determinar si alguna de ellas difiere entre sí. Digamos que estamos analizando datos de un ensayo clínico para el tratamiento de la hipertensión arterial. En el estudio, los voluntarios son aleatorizados a una de tres condiciones: Fármaco 1, Medicamento 2 o placebo. Generemos algunos datos y graficémoslos (ver Figura 28.4)

Figura 28.4: Gráfica de caja que muestra la presión arterial para tres grupos diferentes en nuestro ensayo clínico.

28.6.1 Análisis de varianza

Primero quisiéramos probar la hipótesis nula de que las medias de todos los grupos son iguales —es decir, ninguno de los tratamientos tuvo efecto alguno. Podemos hacer esto usando un método llamado análisis de varianza (ANOVA). Este es uno de los métodos más utilizados en la estadística psicológica, y aquí solo rayaremos la superficie. La idea básica detrás de ANOVA es una que ya discutimos en el capítulo sobre el modelo lineal general, y de hecho ANOVA es solo un nombre para una implementación específica de dicho modelo.

Recuerda del último capítulo que podemos particionar la varianza total en los datos ($SS$) en la varianza que se explica por el modelo ($SS$) y la varianza que no es ($SS$). Entonces podemos calcular un cuadrado medio para cada uno de estos dividiéndolos por sus grados de libertad; para el error esto es$N - p$(donde$p$es el número de medias que hemos calculado), y para el modelo esto es$p - 1$:

$$MS_ {modelo} =\ frac {SS_ {modelo}} {df_ {modelo}} =\ frac {SS_ {modelo}} {p-1}$$

$$MS_ {error} =\ frac {SS_ {error}} {df_ {error}} =\ frac {SS_ {error}} {N - p}$$

Con ANOVA, queremos probar si la varianza contabilizada por el modelo es mayor de lo que esperaríamos por casualidad, bajo la hipótesis nula de no diferencias entre medias. Mientras que para la distribución t el valor esperado es cero bajo la hipótesis nula, ese no es el caso aquí, ya que las sumas de cuadrados son siempre números positivos. Afortunadamente, existe otra distribución estándar que describe cómo se distribuyen las proporciones de sumas de cuadrados bajo la hipótesis nula: La distribución F (ver figura 28.5). Esta distribución tiene dos grados de libertad, que corresponden a los grados de libertad para el numerador (que en este caso es el modelo), y el denominador (que en este caso es el error).

Figura 28.5: Distribuciones F bajo la hipótesis nula, para diferentes valores de grados de libertad.

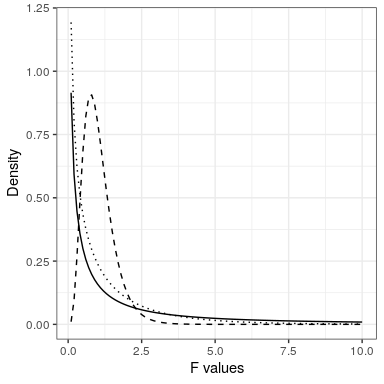
Para crear un modelo ANOVA, ampliamos la idea de codificación ficticia que encontraste en el último capítulo. Recuerde que para la prueba t comparando dos medias, creamos una única variable ficticia que tomó el valor de 1 para una de las condiciones y cero para las demás. Aquí ampliamos esa idea creando dos variables ficticias, una que codifica para el padecimiento Medicamento 1 y otra que codifica para el padecimiento Medicamento 2. Al igual que en la prueba t, tendremos una condición (en este caso, placebo) que no tiene una variable ficticia, y así representa la línea base con la que se comparan las otras; su media define la intercepción del modelo. Vamos a crear la codificación ficticia para los medicamentos 1 y 2.

Ahora podemos encajar un modelo usando el mismo enfoque que usamos en el capítulo anterior:

## 
## Call:
## lm(formula = sysBP ~ d1 + d2, data = df)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -29.084  -7.745  -0.098   7.687  23.431 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   141.60       1.66   85.50  < 2e-16 ***
## d1            -10.24       2.34   -4.37  2.9e-05 ***
## d2             -2.03       2.34   -0.87     0.39    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 9.9 on 105 degrees of freedom
## Multiple R-squared:  0.169,  Adjusted R-squared:  0.154 
## F-statistic: 10.7 on 2 and 105 DF,  p-value: 5.83e-05

El resultado de este comando nos proporciona dos cosas. Primero, nos muestra el resultado de una prueba t para cada una de las variables ficticias, que básicamente nos dicen si cada una de las afecciones difiere por separado del placebo; parece que el Medicamento 1 lo hace mientras que el Medicamento 2 no. No obstante, hay que tener en cuenta que si quisiéramos interpretar estas pruebas, necesitaríamos corregir los valores p para dar cuenta de que hemos realizado múltiples pruebas de hipótesis; veremos un ejemplo de cómo hacerlo en el siguiente capítulo.

Recuerde que la hipótesis que empezamos queriendo probar fue si había alguna diferencia entre alguna de las condiciones; nos referimos a esto como una prueba de hipótesis ómnibus, y es la prueba que proporciona el estadístico F. El estadístico F básicamente nos dice si nuestro modelo es mejor que un modelo simple que solo incluye una intercepción. En este caso vemos que la prueba F es altamente significativa, consistente con nuestra impresión de que sí parecía haber diferencias entre los grupos (que de hecho sabemos que hubo, porque creamos los datos).