1.5: Relaciones de equivalencia
- Page ID
- 152059
Teoría Básica
Una relación\(\approx\) sobre un conjunto no vacío\(S\) que es reflexiva, simétrica y transitiva es una relación de equivalencia sobre\(S\). Así, para todos\( x, \, y, \, z \in S \),
- \( x \approx x \), la propiedad reflexiva.
- Si\( x \approx y \) entonces\( y \approx x \), la propiedad simétrica.
- Si\( x \approx y \) y\( y \approx z \) entonces\( x \approx z \), la propiedad transitiva.
Como sugieren el nombre y la notación, una relación de equivalencia pretende definir un tipo de equivalencia entre los elementos de\(S\). Al igual que los órdenes parciales, las relaciones de equivalencia ocurren de forma natural en la mayoría de las áreas de las matemáticas,
Supongamos que\( \approx \) es una relación de equivalencia sobre\( S \). La clase de equivalencia de un elemento\(x \in S\) es el conjunto de todos los elementos que son equivalentes a\(x\), y se denota\[ [x] = \{y \in S: y \approx x\} \]
Resultados
El resultado más importante es que una relación de equivalencia en un conjunto\(S\) define una partición de\(S\), por medio de las clases de equivalencia.
Supongamos que\(\approx\) es una relación de equivalencia en un conjunto\(S\).
- Si\(x \approx y\) entonces\([x] = [y]\).
- Si\(x \not \approx y\) entonces\([x] \cap [y] = \emptyset\).
- La colección de clases de equivalencia (distintas) es una partición de\( S \) en conjuntos no vacíos.
Prueba
- Supongamos que\( x \approx y \). Si\( u \in [x] \) entonces\( u \approx x \) y\( u \approx y \) por lo tanto por la propiedad transitiva. De ahí\( u \in [y] \). Del mismo modo, si\( u \in [y] \) entonces\( u \approx y \). Pero\( y \approx x \) por la propiedad simétrica, y\( u \approx x \) por lo tanto por la propiedad transitiva. De ahí\( u \in [x] \).
- Supongamos que\( x \not \approx y \). Si\( u \in [x] \cap [y] \), entonces\( u \in [x] \) y\( u \in [y] \), así\( u \approx x \) y\( u \approx y \). Pero luego\( x \approx u \) por la propiedad simétrica, y luego\( x \approx y \) por la propiedad transitiva. Esto es una contradicción, entonces\( [x] \cap [y] = \emptyset \).
- De (a) y (b), las clases de equivalencia (distintas) son disjuntas. Si\( x \in S \), entonces\( x \approx x \) por la propiedad reflexiva, y por lo tanto\( x \in [x] \). Por lo tanto\( \bigcup_{x \in S} [x] = S \).
En ocasiones se denota el conjunto\(\mathscr{S}\) de clases de equivalencia\(S / \approx\). La idea es que las clases de equivalencia son nuevos objetos
obtenidos mediante la identificación
de elementos en los\(S\) que son equivalentes. Por el contrario, cada partición de un conjunto define una relación de equivalencia en el conjunto.
Supongamos que\(\mathscr{S}\) es una colección de conjuntos no vacíos que particionan un conjunto dado\(S\). Definir la relación\( \approx \) sobre\( S \) por\( x \approx y \) si y solo si\( x \in A \) y\( y \in A \) para algunos\( A \in \mathscr{S} \).
- \( \approx \)es una relación de equivalencia.
- \( \mathscr{S} \)es el conjunto de clases de equivalencia.
Prueba
- Si\( x \in S \), entonces\( x \in A \) para algunos\( A \in \mathscr{S} \), desde\( \mathscr{S} \) particiones\( S \). De ahí\( x \approx x \), y así se mantiene la propiedad reflexiva. A continuación,\( \approx \) es trivialmente simétrico por definición. Por último, supongamos que\( x \approx y \) y\( y \approx z \). Entonces\( x, \, y \in A \) para algunos\( A \in \mathscr{S} \) y\( y, \, z \in B \) para algunos\( B \in \mathscr{S} \). Pero entonces\( y \in A \cap B \). Los sets en\( \mathscr{S} \) son disjuntos, entonces\( A = B \). De ahí\( x, \, z \in A \), así\( x \approx z \). Así\( \approx \) es transitivo.
- Si\( x \in S \), entonces\( x \in A \) para un único\( A \in \mathscr{S} \), y luego por definición,\( [x] = A \).
A veces se denota la relación de equivalencia\(\approx\) asociada a\(\mathscr{S}\) una partición dada\(S / \mathscr{S}\). La idea, por supuesto, es que los elementos del mismo conjunto de la partición sean equivalentes.
El proceso de formar una partición a partir de una relación de equivalencia, y el proceso de formar una relación de equivalencia a partir de una partición son inversos entre sí.
- Si comenzamos con una relación de equivalencia\(\approx\) on\(S\), formamos la partición asociada, y luego construimos la relación de equivalencia asociada con la partición, entonces terminamos con la relación de equivalencia original. En notación modular,\(S \big/ (S / \approx)\) es lo mismo que\(\approx\).
- Si comenzamos con una partición\(\mathscr{S}\) de\(S\), formamos la relación de equivalencia asociada, y luego formamos la partición asociada con la relación de equivalencia, entonces terminamos con la partición original. En notación modular,\(S \big/ (S / \mathscr{S})\) es lo mismo que\(\mathscr{S}\).
Supongamos que\( S \) es un conjunto no vacío. La relación de equivalencia más básica\( S \) es la relación de igualdad\( = \). En este caso\( [x] = \{x\} \) para cada uno\( x \in S \). En el otro extremo está la relación trivial\( \approx \) definida por\( x \approx y \) para todos\( x, \, y \in S \). En este caso\( S \) es la única clase de equivalencia.
Cada función\(f\) define una relación de equivalencia en su dominio, conocida como la relación de equivalencia asociada con\(f\). Además, las clases de equivalencia tienen una descripción simple en términos de las imágenes inversas de\(f\).
Supongamos que\(f: S \to T\). Definir la relación\(\approx\) en\(S\) por\(x \approx y\) si y solo si\(f(x) = f(y)\).
- La relación\(\approx\) es una relación de equivalencia sobre\(S\).
- El conjunto de clases de equivalencias es\(\mathscr{S} = \left\{f^{-1}\{t\}: t \in \range(f)\right\}\).
- La función\(F: \mathscr{S} \to T\) definida por\(F([x]) = f(x)\) está bien definida y es uno-a-uno.
Prueba
- Si\( x \in S \) entonces trivialmente\( f(x) = f(x) \), así\( x \approx x \). De ahí\( \approx \) que sea reflexivo. Si\( x \approx y \) entonces es\( f(x) = f(y) \) así trivialmente\( f(y) = f(x) \) y por lo tanto\( y \approx x \). Así\( \approx \) es simétrico. Si\( x \approx y \) y\( y \approx z \) entonces\( f(x) = f(y) \) y\( f(y) = f(z) \), tan trivialmente\( f(x) = f(z) \) y así\( x \approx z \). De ahí\( \approx \) que sea transitivo.
- Recordemos que\( t \in \range(f) \) si y solo si\( f(x) = t \) para algunos\( x \in S \). Entonces por definición,\( [x] = f^{-1}\{t\} = \{y \in S: f(y) = t\} = \{ y \in S: f(y) = f(x)\} \)
- De (3),\( [x] = [y] \) si y solo si y solo\( x \approx y \) si y solo si\( f(x) = f(y) \). Esto muestra tanto que\( F \) está bien definido, como que\( F \) es uno a uno.
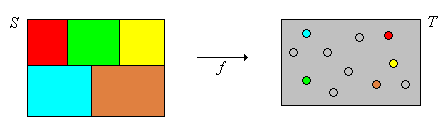
Supongamos otra vez eso\(f: S \to T\).
- Si\(f\) es uno a uno entonces la relación de equivalencia asociada\(f\) es la relación de igualdad, y por lo tanto\([x] = \{x\}\) para cada uno\(x \in S\).
- Si\(f\) es una función constante entonces la relación de equivalencia asociada a\(f\) es la relación trivial, y por lo tanto\(S\) es la única clase de equivalencia.
Prueba
- Si\( f \) es uno a uno, entonces\( x \approx y \) si y solo si y solo\( f(x) = f(y) \) si y solo si\( x = y \).
- Si\( f \) es constante en\( S \) entonces\( f(x) = f(y) \) y por lo tanto\( x \approx y \) para todos\( x, \, y \in S \).
Las relaciones de equivalencia asociadas a funciones son universales: toda relación de equivalencia es de esta forma:
Supongamos que\(\approx\) es una relación de equivalencia en un conjunto\(S\). Definir\(f: S \to \mathscr{P}(S)\) por\(f(x) = [x]\). Entonces\(\approx\) es la relación de equivalencia asociada con\(f\).
Prueba
De (6),\( x \approx y \) si y solo si y solo\( [x] = [y] \) si y solo si\( f(x) = f(y) \).
La intersección de dos relaciones de equivalencia es otra relación de equivalencia.
Supongamos que\(\approx\) y\(\cong\) son relaciones de equivalencia en un conjunto\(S\). Let\(\equiv\) denotar la intersección de\(\approx\) y\(\cong\) (pensado como subconjuntos de\(S \times S\)). Equivalentemente,\(x \equiv y\) si y sólo si\(x \approx y\) y\(x \cong y\).
- \(\equiv\)es una relación de equivalencia sobre\(S\).
- \([x]_\equiv = [x]_\approx \cap [x]_\cong\).
Supongamos que tenemos una relación reflexiva y transitiva, pero que deja de ser un orden parcial porque no es antisimétrica. La relación y su inversa conducen naturalmente a una relación de equivalencia, y luego a su vez, la relación original define un verdadero orden parcial sobre las clases de equivalencia. Esta es una construcción común, y los detalles se dan en el siguiente teorema.
Supongamos que\(\preceq\) es una relación sobre un conjunto\(S\) que es reflexiva y transitiva. Definir la relación\(\approx\) en\(S\) por\(x \approx y\) si y solo si\(x \preceq y\) y\(y \preceq x\).
- \(\approx\)es una relación de equivalencia sobre\(S\).
- Si\(A\) y\(B\) son clases de equivalencia y\(x \preceq y\) para algunos\(x \in A\) y\(y \in B\), entonces\(u \preceq v\) para todos\(u \in A\) y\(v \in B\).
- Definir la relación\(\preceq\) sobre la colección de clases de equivalencia\(\mathscr{S}\) por\(A \preceq B\) si y solo si\(x \preceq y\) para algunos (y por lo tanto todos)\(x \in A\) y\(y \in B\). Entonces\(\preceq\) es un orden parcial encendido\(\mathscr{S}\).
Prueba
- Si\( x \in S \) entonces\( x \preceq x \) ya\( \preceq \) es reflexivo. De ahí\( x \approx x \) que así\( \approx \) sea reflexivo. Claramente\( \approx \) es simétrico por la simetría de la definición. Supongamos que\( x \approx y \) y\( y \approx z \). Entonces\( x \preceq y \),\( y \preceq z \),\( z \preceq y \) y\( y \preceq x \). De ahí\( x \preceq z \) y\( z \preceq x \) desde\( \preceq \) es transitivo. Por lo\( x \approx z \) tanto, así\( \approx \) es transitivo.
- Supongamos que\( A \) y\( B \) son clases de equivalencia de\( \approx \) y que\( x \preceq y \) para algunos\( x \in A \) y\( y \in B \). Si\( u \in A \) y\( v \in B \), entonces\( x \approx u \) y\( y \approx v \). Por lo tanto\( u \preceq x \) y\( y \preceq v \). Por transitividad,\( u \preceq v \).
- Supongamos que\( A \in \mathscr{S} \). Si\( x, \, y \in A \) entonces\( x \approx y \) y por lo tanto\( x \preceq y \). Por lo tanto\( A \preceq A \) y así\( \preceq \) es reflexivo. Siguiente supongamos eso\( A, \, B \in \mathscr{S} \) y eso\( A \preceq B \) y\( B \preceq A \). Si\( x \in A \) y\( y \in B \) entonces\( x \preceq y \) y\( y \preceq x \). De ahí\( x \approx y \) que así\( A = B \). Por lo tanto\( \preceq \) es antisimétrico. Por último, supongamos que\( A, \, B, \, C \in \mathscr{S} \) y eso\( A \preceq B \) y\( B \preceq C \). Tenga en cuenta que\( B \ne \emptyset \) así que vamos\( y \in B \). Si\( x \in A, \, z \in C \) entonces\( x \preceq y \) y\( y \preceq z \). De ahí\( x \preceq z \) y por lo tanto\( A \preceq C \). Así\( \preceq \) es transitivo.
Un excelente ejemplo de la construcción en el teorema anterior ocurre cuando tenemos una función cuyo espacio de rango está parcialmente ordenado. Podemos construir un orden parcial sobre las clases de equivalencia en el dominio que están asociadas a la función.
Supongamos que\(S\) y\(T\) son conjuntos y que\(\preceq_T\) es un orden parcial encendido\(T\). Supongamos también eso\(f: S \to T\). Definir la relación\(\preceq_S\) en\(S\) por\(x \preceq_S y\) si y solo si\(f(x) \preceq_T f(y)\).
- \(\preceq_S\)es reflexiva y transitiva.
- La relación de equivalencia sobre\(S\) construido en (10) es la relación de equivalencia asociada con\(f\), como en (6).
- \(\preceq_S\)se puede extender a un orden parcial sobre las clases de equivalencia correspondientes a\(f\).
Prueba
- Si\( x \in S \) entonces\( f(x) \preceq_T f(x) \) ya\( \preceq_T \) es reflexivo, y por lo tanto\( x \preceq_S x \). Así\( \preceq_S \) es reflexivo. Supongamos eso\( x, \, y, \, z \in S \) y eso\(x \preceq_S y \) y\( y \preceq_S z \). Entonces\( f(x) \preceq_T f(y) \) y\( f(y) \preceq_T f(z) \). De ahí\( f(x) \preceq_T f(z) \) ya que\( \preceq_T \) es transitivo. Así\( \preceq_S \) es transitivo.
- Para la relación de equivalencia\( \approx \) sobre\( S \) construido en (10),\( x \approx y \) si y solo si\( x \preceq_S y \) y si y solo\( y \preceq_S x \) si y si\( f(x) \preceq_T f(y) \) y solo\( f(y) \preceq_T f(x) \) si y solo si\( f(x) = f(y) \), ya que\( \preceq_T \) es antisimétrico. Así\( \approx \) es la relación de equivalencia asociada a\( f \).
- Esto se desprende inmediatamente de (10) y partes (a) y (b). Si\( u, \, v \in \range(f) \), entonces\( f^{-1}(\{u\}) \preceq_S f^{-1}(\{v\}) \) si y solo si\( u \preceq_T v \).
Ejemplos y Aplicaciones
Funciones simples
Dar las clases de equivalencia explícitamente para las funciones desde\(\R\) dentro\(\R\) definidas a continuación:
- \(f(x) = x^2\).
- \(g(x) = \lfloor x \rfloor\).
- \(h(x) = \sin(x)\).
Responder
- \([x] = \{x, -x\}\)
- \([x] = \left[ \lfloor x \rfloor, \lfloor x \rfloor + 1 \right)\)
- \([x] = \{x + 2 n \pi: n \in \Z\} \cup \{(2 n + 1) \pi - x: n \in \Z\}\)
Cálculo
Supongamos que\(I\) es un intervalo fijo de\(\R\), y ese\(S\) es el conjunto de funciones diferenciables desde\(I\) dentro\(\R\). Considerar la relación de equivalencia asociada con el operador derivado\(D\) on\(S\), para que\(D(f) = f^{\prime}\). Para\(f \in S\), dar una descripción simple de\([f]\).
Responder
\([f] = \{f + c: c \in \R\}\)
Congruencia
Recordemos la relación\( \mid \) de división de\( \N_+\) a\( \Z \): Para\( d \in \N_+ \) y\( n \in \Z \),\( d \mid n \) significa que\( n = k d \) para algunos\( k \in \Z \). En palabras,\( d \) divide\( n \) o equivalentemente\( n \) es un múltiplo de\( d \). En el apartado anterior, demostramos que\( \mid \) es una orden parcial sobre\( \N_+ \).
Arreglar\( d \in \N_+ \).
- Definir la relación\(\equiv_d\) en\(\Z\) por\(m \equiv_d n\) si y solo si\(d \mid (n - m)\). La relación\(\equiv_d\) se conoce como módulo de congruencia\(d\).
- Dejar\(r_d: \Z \to \{0, 1, \ldots, d - 1\}\) definirse de manera que\(r(n)\) sea el resto cuando\(n\) se divide por\(d\).
Recordemos que por el teorema de la división euclidiana, llamado así por Euclides por supuesto, se\( n \in \Z \) puede escribir de manera única en la forma\( n = k d + q \) donde\( k \in \Z \) y\( q \in \{0, 1, \ldots, d - 1\} \), y luego\( r_d(n) = q \).
Congruencia módulo\( d \).
- \( \equiv_d \)es la relación de equivalencia asociada a la función\( r_d \).
- Hay\( d \) distintas clases de equivalencia, dadas por\( [q]_d = \{q + k d: k \in \Z\}\) for\( q \in \{0, 1, \ldots, d - 1\} \).
Prueba
- Recordemos que para la relación de equivalencia asociada a\( r_d \), los enteros\( m \) y\( n \) son equivalentes si y solo si\( r_d(m) = r_d(n) \). Por el teorema de la división\( n = k d + q \),\( m = j d + p \) y, dónde\( j, \, k \in \Z \) y\( p, \, q \in \{0. 1, \ldots, d - 1\} \), y estas representaciones son únicas. Así\( n - m = (k - j) d + (q - p) \), y así\( m \equiv_d n \) si y sólo si y sólo\( d \mid (n - m) \) si y sólo si y sólo\( p = q \) si y sólo si\( r_d(m) = r_d(n) \).
- Recordemos que las clases de equivalencia son\( r_d^{-1}\{q\} \) para\( q \in \range\left(r_d\right) = \{0, 1, \ldots, d - 1\} \). Por el teorema de la división,\( r_d^{-1}\{q\} = \{k d + q: k \in \Z\}\).
Dar explícitamente las clases de equivalencia para\( \equiv_4 \), congruencia mod 4.
Responder
- \( [0]_4 = \{0, 4, 8, 12, \ldots\} \cup \{-4, -8, -12, -16, \ldots\} \)
- \( [1]_4 = \{1, 5, 9, 13, \ldots\} \cup \{-3, -7, -11, -15, \ldots\} \)
- \( [2]_4 = \{2, 6, 10, 14, \ldots\} \cup \{-2, -6, -10, -14, \ldots\} \)
- \( [3]_4 = \{3, 7, 11, 15, \ldots\} \cup \{-1, -5, -9, -13, \ldots\} \)
Álgebra lineal
El álgebra lineal proporciona varios ejemplos de relaciones de equivalencia importantes e interesantes. Para poner el escenario, vamos a\(\R^{m \times n}\) denotar el conjunto de\(m \times n\) matrices con entradas reales, para\( m, \, n \in \N_+ \).
Recordemos que las siguientes son operaciones de fila en una matriz:
- Multiplica una fila por un número real distinto de cero.
- Intercambien dos filas.
- Agrega un múltiplo de una fila a otra fila.
Las operaciones de fila son esenciales para invertir matrices y resolver sistemas de ecuaciones lineales.
Las matrices\(A, \, B \in \R^{m \times n}\) son equivalentes de fila si se\(A\) pueden transformar en\(B\) mediante una secuencia finita de operaciones de fila. La equivalencia de fila es una relación de equivalencia sobre\(\R^{m \times n}\).
Prueba.
Si\( A \in \R^{m \times n} \), entonces\( A \) es fila equivalente a sí misma: simplemente no podemos hacer nada, o si lo prefiere, podemos multiplicar la primera fila de\( A \) por 1. Para la simetría, la clave es que cada operación de fila se puede revertir por otra operación de fila: multiplicar una fila por\( c \ne 0 \) se invierte multiplicando la misma fila de la matriz resultante por\( 1 / c \). El cambio de dos filas se invierte intercambiando las mismas dos filas de la matriz resultante. Agregar\( c \) tiempos fila\( i \) a fila\( j \) se invierte agregando\( -c \) tiempos fila\( i \) a fila\( j \) en la matriz resultante. Por lo tanto, si podemos\( A \) transformarnos en\( B \) por una secuencia finita de operaciones de fila, entonces podemos\( B \) transformarnos en\( A \) aplicando las operaciones de fila invertida en el orden inverso. La transitividad es clara: Si podemos\( A \) transformarnos en\( B \) por una secuencia de operaciones de fila y\( B \) en\( C \) por otra secuencia de operaciones de fila, entonces podemos\( A \) transformarnos en\( C \) juntando las dos secuencias.
Nuestra siguiente relación involucra la similitud, lo cual es muy importante en el estudio de las transformaciones lineales, el cambio de base y la teoría de los valores propios y vectores propios.
Las matrices\(A, \, B \in \R^{n \times n}\) son similares si existe un invertible\(P \in \R^{n \times n}\) tal que\(P^{-1} A P = B\). La similitud es una relación de equivalencia sobre\(\R^{n \times n}\).
Prueba
Si\( A \in \R^{n \times n} \) entonces\( A = I^{-1} A I \), dónde\( I \) está la matriz de\( n \times n \) identidad, entonces\( A \) es similar a sí misma. Supongamos que\( A, \, B \in \R^{n \times n} \) y eso\( A \) es similar a\( B \) así que\( B = P^{-1} A P\) para algunos invertibles\( P \in \R^{n \times n} \). Entonces\( A = P B P^{-1} = \left(P^{-1}\right)^{-1} B P^{-1} \) así\( B \) es similar a\( A \). Por último, supongamos que eso\( A, \, B, \, C \in R^{n \times n} \) y eso\( A \) es similar\( B \) y que\( B \) es similar a\( C \). Entonces\( B = P^{-1} A P \) y\( C = Q^{-1} B Q \) para algunos invertibles\( P, \, Q \in R^{n \times n} \). Entonces\( C = Q^{-1} P^{-1} A P Q = (P Q)^{-1} A (P Q) \), así\( A \) es similar a\( C \).
A continuación recordemos que para\( A \in \R^{m \times n} \), la transposición de\( A \) es la matriz\( A^T \in \R^{n \times m} \) con la propiedad de la que\( (i, j) \) entrada\( A \) es la\( (j, i) \) entrada de\( A^T \), para\( i, \, j \in \{1, 2, \ldots, m\} \). En pocas palabras,\( A^T\) es la matriz cuyas filas son las columnas de\( A \). Para el teorema que sigue, hay que recordar que\( (A B)^T = B^T A^T \) para\( A \in \R^{m \times n} \) y\( B \in \R^{n \times k} \), y\( \left(A^T\right)^{-1} = \left(A^{-1}\right)^T \) si\( A \in \R^{n \times n} \) es invertible.
Las matrices\( A, \, B \in \R^{n \times n} \) son congruentes si existe un invertible\( P \in \R^{n \times n} \) tal que\( B = P^T A P \). La congruencia es una relación de equivalencia sobre\( \R^{n \times n} \)
Prueba
Si\( A \in \R^{n \times n} \) entonces\( A = I^T A I \), donde de nuevo\( I \) está la matriz de\( n \times n \) identidad, así\( A \) es congruente consigo misma. Supongamos que\( A, \, B \in \R^{n \times n} \) y eso\( A \) es congruente con\( B \) así que\( B = P^T A P\) para algunos invertibles\( P \in \R^{n \times n} \). Entonces\( A = \left(P^T\right)^{-1} B P^{-1} = \left(P^{-1}\right)^T B P^{-1} \) así\( B \) es congruente con\( A \). Por último, supongamos que eso\( A, \, B, \, C \in R^{n \times n} \) y eso\( A \) es congruente con\( B \) y eso\( B \) congruente con\( C \). Entonces\( B = P^T A P \) y\( C = Q^T B Q \) para algunos invertibles\( P, \, Q \in R^{n \times n} \). Entonces\( C = Q^T P^T A P Q = (P Q)^T A (P Q) \), así\( A \) es congruente con\( C \).
La congruencia es importante en el estudio de las matrices ortogonales y el cambio de bases. Por supuesto, el término congruencia aplicado a las matrices no debe confundirse con el mismo término aplicado a los enteros.
Sistemas numéricos
Las relaciones de equivalencia juegan un papel importante en la construcción de estructuras matemáticas complejas a partir de estructuras matemáticas más simples. A menudo los objetos en la nueva estructura son clases de equivalencia de objetos construidos a partir de las estructuras más simples, módulo una relación de equivalencia que captura las propiedades esenciales de los nuevos objetos.
La construcción de sistemas numéricos es un excelente ejemplo de esta idea general. El siguiente ejercicio explora la construcción de números racionales a partir de enteros.
Definir una relación\(\approx\) sobre\(\Z \times \N_+\) por\((j, k) \approx (m, n)\) si y solo si\(j\,n = k\,m\).
- \(\approx\)es una relación de equivalencia.
- Definir\(\frac{m}{n} = [(m, n)]\), la clase de equivalencia generada por\((m, n)\), para\(m \in \Z\) y\(n \in \N_+\). Esta definición captura las propiedades esenciales de los números racionales.
Prueba
- Para\( (m, n) \in \Z \times \N_+ \), por\( m n = n m \) supuesto, así\( (m, n) \approx (m, n) \). De ahí\( \approx \) que sea reflexivo. Si\( (j, k), \, (m, n) \in \Z \times \N_+ \) y\( (j, k) \approx (m, n) \), entonces\( j n = k m \) tan trivialmente\( m k = n j\), y por lo tanto\( (m, n) \approx (j, k) \). Así\( \approx \) es simétrico. Por último, supongamos que\( (j, k), \, (m, n), \, (p, q) \in \Z \times \N_+ \) y eso\( (j, k) \approx (m, n) \) y\( (m, n) \approx (p, q) \). Entonces\( j n = k m \) y\( m q = n p \), así lo\( j n p = k m p \) que implica\( j m q = k m p \), y así\( j q = k p \). De ahí\( (j, k) \approx (p, q) \) que así\( \approx \) sea transitivo.
- Supongamos que\(\frac{j}{k}\) y\(\frac{m}{n} \) son números racionales en el sentido habitual, informal, dónde\( j, \, m \in \Z \) y\( k, \, n \in \N_+ \). Entonces\( \frac{j}{k} = \frac{m}{n} \) si y solo\( j n = k m \) si y solo si\( (j, k) \approx (m, n) \), entonces tiene sentido definir\( \frac{m}{n} \) como la clase de equivalencia generada por\( (m, n) \). La suma y la multiplicación se definen de la manera habitual: si\( (j, k), \, (m, n) \in \Z \times \N_+ \) entonces\[ \frac{j}{k} + \frac{m}{n} = \frac{j n + m k}{k n}, \ \ \frac{j}{k} \cdot \frac{m}{n} = \frac{j m}{k n} \] Las definiciones son consistentes; es decir, no dependen de las representaciones particulares de las clases de equivalencia.


