2.7: Medir espacios
- Page ID
- 152167
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección discutimos los espacios de medida positiva (que incluyen espacios de probabilidad) desde un punto de vista más avanzado. Las secciones de Teoría de Medidas y Estructuras Especiales de Conjuntos en el capítulo de Fundaciones son requisitos previos esenciales. Por otro lado, si no te interesan los aspectos teóricos de medición de la probabilidad, puedes saltarte con seguridad esta sección.
Medida Positiva
Definiciones
Supongamos que\( S \) es un conjunto, desempeñando el papel de un conjunto universal para una teoría matemática. Como hemos señalado antes,\( S \) generalmente viene con un\( \sigma \) -álgebra\( \mathscr S \) de subconjuntos admisibles de\( S \), por lo que\( (S, \mathscr S) \) es un espacio medible. En particular, este es el caso del modelo de un experimento aleatorio, donde\( S \) está el conjunto de resultados y\( \mathscr S \) la\( \sigma \) -álgebra de eventos, de manera que el espacio medible\( (S, \mathscr S) \) es el espacio muestral del experimento. Una medida de probabilidad es un caso especial de un objeto más general conocido como medida positiva.
Una medida positiva\((S, \mathscr S)\) es una función\(\mu: \mathscr S \to [0, \infty] \) que satisface los siguientes axiomas:
- \( \mu(\emptyset) = 0 \)
- Si\(\{A_i: i \in I\}\) es una colección disjunta contable, por pares, de conjuntos en\(\mathscr S\) entonces\[\mu\left(\bigcup_{i \in I} A_i\right) = \sum_{i \in I} \mu(A_i)\]
El triple\((S, \mathscr S, \mu)\) es un espacio de medida.
El axioma (b) se llama aditividad contable, y es la propiedad esencial. La medida de un conjunto que consiste en una unión contable de piezas disjuntas es la suma de las medidas de las piezas. Obsérvese también que dado que los términos en la suma son positivos, no hay problema con el orden de los términos en la suma, aunque claro,\( \infty \) es un valor posible.
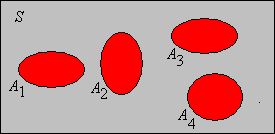.png)
Entonces, tal vez el término espacio medible para\( (S, \mathscr S) \) tenga un poco más de sentido ahora, un espacio medible es aquel que puede tener una medida positiva definida en él.
Supongamos que\( (S, \mathscr S, \mu) \) es un espacio de medida.
- Si\( \mu(S) \lt \infty \) entonces\( (S, \mathscr S, \mu) \) es un espacio de medida finita.
- Si\( \mu(S) = 1 \) entonces\( (S, \mathscr S, \mu) \) es un espacio de probabilidad.
Entonces las medidas de probabilidad son medidas positivas, pero las medidas positivas son importantes más allá de la aplicación a la probabilidad. Las medidas estándar en los espacios euclidianos son todas medidas positivas: la extensión de la longitud para subconjuntos medibles de\( \R \), la extensión del área para subconjuntos medibles de\( \R^2 \), la extensión del volumen para subconjuntos mensurables de\( \R^3 \), y la análogos de dimensiones superiores. De hecho, construiremos estas medidas en la siguiente sección sobre Existencia y Singularidad. Además, la medida de conteo\( \# \) es una medida positiva en los subconjuntos de un conjunto\( S \). En el capítulo sobre Distribuciones se exploran medidas aún más generales que pueden tomar valores positivos y negativos.
Propiedades
Los siguientes resultados dan algunas propiedades simples de un espacio de medida positiva\( (S, \mathscr S, \mu) \). Las pruebas son esencialmente idénticas a las pruebas de las correspondientes propiedades de probabilidad, salvo que la medida de un conjunto puede ser infinita por lo que debemos tener cuidado de evitar la temida forma indeterminada\( \infty - \infty \).
Si\( A, \, B \in \mathscr S \), entonces\( \mu(B) = \mu(A \cap B) + \mu(B \setminus A) \).
Prueba
Tenga en cuenta que\( B = (A \cap B) \cup (B \setminus A) \), y los conjuntos en la unión son disjuntos.
Si\( A, \, B \in \mathscr S \) y\( A \subseteq B \) entonces
- \( \mu(B) = \mu(A) + \mu(B \setminus A) \)
- \( \mu(A) \le \mu(B) \)
Prueba
La parte (a) se desprende del teorema anterior, ya que\( A \cap B = A \). La parte b) se desprende de la parte a).
Así\( \mu \) es una función creciente, relativa al orden parcial del subconjunto\( \subseteq \) encendido\( \mathscr S \) y el orden ordinario\( \le \) encendido\( [0, \infty] \). En particular, si\( \mu \) es una medida finita, entonces\( \mu(A) \lt \infty \) para cada\( A \in \mathscr S \). Tenga en cuenta también que si\( A, \, B \in \mathscr S \) y\( \mu(B) \lt \infty \) entonces\( \mu(B \setminus A) = \mu(B) - \mu(A \cap B) \). En el caso especial que\( A \subseteq B \), esto se convierte\( \mu(B \setminus A) = \mu(B) - \mu(A) \). En particular, estos resultados se mantienen para una medida finita y son como las reglas de diferencia para la probabilidad. Si\( \mu \) es una medida finita, entonces\( \mu(A^c) = \mu(S) - \mu(A) \). Este es el análogo de la regla del complemento en probabilidad, con pero con\( \mu(S) \) reemplazo 1.
El siguiente resultado es el análogo de la desigualdad de Boole para la probabilidad. Para una medida positiva general, el resultado se conoce como la propiedad subaditiva.
Supongamos que\( A_i \in \mathscr S \) para\( i \) en un conjunto de índices contables\( I \). Entonces\[ \mu\left(\bigcup_{i \in I} A_i \right) \le \sum_{i \in I} \mu(A_i) \]
Prueba
La prueba es exaclty como la de la desigualdad de Boole. Asumir eso\( I = \N_+ \). Dejar\( B_1 = A_1 \) y\( B_i = A_i \setminus (A_1 \cup \ldots \cup A_{i-1}) \) para\( i \in \{2, 3, \ldots\} \). Entonces\( \{B_i: i \in I\} \) es una colección disjunta de conjuntos en\( \mathscr S \) con la misma unión que\( \{A_i: i \in I\} \). También\( B_i \subseteq A_i \) para cada uno\( i \) así\( \mu(B_i) \le \mu(A_i) \). De ahí\[ \mu\left(\bigcup_{i \in I} A_i \right) = \mu\left(\bigcup_{i \in I} B_i \right) = \sum_{i \in I} \mu(B_i) \le \sum_{i \in I} \mu(A_i) \]
Para una unión de conjuntos con medida finita, se mantiene la fórmula de inclusión-exclusión, y la prueba es igual que la de probabilidad.
Supongamos que\(A_i \in \mathscr S\) para cada\(i \in I\) donde\(\#(I) = n\), y eso\( \mu(A_i) \lt \infty \) para\( i \in I \). Entonces\[\mu \left( \bigcup_{i \in I} A_i \right) = \sum_{k = 1}^n (-1)^{k - 1} \sum_{J \subseteq I, \; \#(J) = k} \mu \left( \bigcap_{j \in J} A_j \right)\]
Prueba
La prueba es por inducción en\(n\). La prueba para\( n = 2 \) es simple:\( A_1 \cup A_2 = A_1 \cup (A_2 \setminus A_1) \). La unión de la derecha es disjunta, por lo que usando la aditividad y la regla de diferencia,\[ \mu(A_1 \cup A_2) = \mu (A_1) + \mu(A_2 \setminus A_1) = \mu(A_1) + \mu(A_2) - \mu(A_1 \cap A_2) \] Supongamos ahora que la fórmula de inclusión-exclusión se mantiene para un dado\( n \in \N_+ \), y considerar el caso\( n + 1 \). Entonces\[ \bigcup_{i=1}^{n + 1} A_i = \left(\bigcup_{i=1}^n A_i \right) \cup \left[ A_{n+1} \setminus \left(\bigcup_{i=1}^n A_i\right) \right] \] como antes, el conjunto entre paréntesis y el conjunto entre corchetes son disjuntos. Así, usando el axioma de aditividad, la regla de diferencia, y la regla distributiva que tenemos\[ \mu\left(\bigcup_{i=1}^{n+1} A_i\right) = \mu\left(\bigcup_{i=1}^n A_i\right) + \mu(A_{n+1}) - \mu\left(\bigcup_{i=1}^n (A_{n+1} \cap A_i) \right) \] Por la hipótesis de inducción, la fórmula de inclusión-exclusión se mantiene para cada unión de\( n \) conjuntos a la derecha. Aplicar la fórmula y simplificar da la fórmula de inclusión-exclusión para\( n + 1 \) conjuntos.
El teorema de continuidad para conjuntos crecientes se mantiene para una medida positiva. El teorema de continuidad para eventos decrecientes se mantiene también, si los conjuntos tienen medida finita. Nuevamente, las pruebas son similares a las de una medida de probabilidad, a excepción de consideraciones de medida infinita.
Supongamos que\( (A_1, A_2, \ldots) \) es una secuencia de conjuntos en\( \mathscr S \).
- Si la secuencia va en aumento entonces\( \mu\left(\bigcup_{i=1}^\infty A_i \right) = \lim_{n \to \infty} \mu(A_n) \).
- Si la secuencia es decreciente y\( \mu(A_1) \lt \infty \) luego\( \mu\left(\bigcap_{i=1}^\infty A_i \right) = \lim_{n \to \infty} \mu(A_n) \).
Prueba
- Tenga en cuenta que si\( \mu(A_k) = \infty \) para algunos\( k \) entonces\( \mu(A_n) = \infty \) para\( n \ge k \) y\( \mu\left(\bigcup_{i=1}^\infty A_i \right) = \infty \). Así, supongamos que\( \mu(A_i) \lt \infty \) para cada uno\( i \). Dejar\( B_1 = A_1 \) y\( B_i = A_i \setminus A_{i-1} \) para\( i \in \{2, 3, \ldots\} \). Entonces\( (B_1, B_2, \ldots) \) es una secuencia disjunta con la misma unión que\( (A_1, A_2, \ldots) \). También,\( \mu(B_1) = \mu(A_1) \) y por la regla de diferencia apropiada,\( \mu(B_i) = \mu(A_i) - \mu(A_{i-1}) \) para\( i \in \{2, 3, \ldots\} \). De ahí\[ \mu\left(\bigcup_{i=1}^\infty A_i \right) = \mu \left(\bigcup_{i=1}^\infty B_i \right) = \sum_{i=1}^\infty \mu(B_i) = \lim_{n \to \infty} \sum_{i=1}^n \mu(B_i) \] Pero\( \sum_{i=1}^n \mu(B_i) = \mu(A_1) + \sum_{i=2}^n [\mu(A_i) - \mu(A_{i-1})] = \mu(A_n) \).
- Tenga en cuenta que\( A_1 \setminus A_n \) está aumentando en\( n \). Por lo tanto, usando el resultado de continuidad para conjuntos crecientes,\ begin {align}\ mu\ left (\ bigcap_ {i=1} ^\ infty a_i\ right) & =\ mu\ left [A_1\ setless\ bigcup_ {i=1} ^\ infty (A_1\ setless a_i)\ right] =\ mu (A_1) -\ mu\ left [\ bigcup_ {i=1}\ infty (A_1\ setmenos a_N)\ derecha]\\ & =\ mu (A_1) -\ lim_ {n\ a\ infty}\ mu (A_1\ setmenos a_n) =\ mu (A_1) -\ lim_ {n\ a\ infty}\ izquierda [\ mu (A_1) -\ mu (a_N)\ derecha] =\ lim_ {n\ a\ infty}\ mu (a_N)\ end {align}
Recordemos que si\( (A_1, A_2, \ldots) \) está aumentando,\( \bigcup_{i=1}^\infty A_i \) se denota\( \lim_{n \to \infty} A_n \), y si\( (A_1, A_2, \ldots) \) es decreciente,\( \bigcap_{i=1}^\infty A_i \) se denota\( \lim_{n \to \infty} A_n \). En ambos casos, el teorema de continuidad tiene la forma\( \mu\left(\lim_{n \to \infty} A_n\right) = \lim_{n \to \infty} \mu(A_n) \). El teorema de continuidad para eventos decrecientes falla sin la suposición adicional de medida finita. A continuación se da un simple contraejemplo.
El siguiente corolario de la ley de inclusión-exclusión da una condición para la aditividad contable que no requiere que los conjuntos sean disjuntos, sino sólo que las intersecciones tengan medida 0. El resultado se utiliza a continuación en el teorema al finalizar.
Supongamos que\( A_i \in \mathscr S \) para cada uno\( i \) en un conjunto de índices contables\( I \) y que\( \mu(A_i) \lt \infty \) para\( i \in I \) y\( \mu(A_i \cap A_j) = 0 \) para distintos\( i, \, j \in I \). Entonces\[ \mu\left(\bigcup_{i \in I} A_i \right) = \sum_{i \in I} \mu(A_i) \]
Prueba
Eso vamos a suponer\( I = \N_+ \). Porque\( n \in \N_+ \),\[ \mu\left(\bigcup_{i=1}^n A_i\right) = \sum_{i=1}^n \mu(A_i) \] como consecuencia inmediata de la ley de inclusión-exclusión, bajo el supuesto de que\( \mu(A_i \cap A_j) = 0 \) para distinto\( i, j \in \{1, 2, \ldots, n\} \). Siguiente\( \bigcup_{i=1}^n A_i \uparrow \bigcup_{i=1}^\infty A_i \) como\( n \to \infty \), y por lo tanto por el teorema de continuidad para eventos crecientes,\( \mu\left(\bigcup_{i=1}^n A_i\right) \to \mu\left(\bigcup_{i=1}^\infty A_i\right) \) como\( n \to \infty \). Por otro lado,\( \sum_{i=1}^n \mu(A_i) \to \sum_{i=1}^\infty \mu(A_i) \) como\( n \to \infty \) por la definición de una serie infinita de términos no negativos.
Más Definiciones
Si una medida positiva no es finita, entonces la siguiente definición da lo mejor que sigue.
El espacio de medida\( (S, \mathscr S, \mu) \) es \( \sigma \)-finito si existe una colección contable\(\{A_i: i \in I\} \subseteq \mathscr S\) con\( \bigcup_{i \in I} A_i = S \) y\( \mu(A_i) \lt \infty \) para cada uno\( i \in I \).
Entonces claro, si\(\mu\) es una medida finita en\((S, \mathscr S)\) entonces\(\mu\) es\(\sigma\) -finita, pero no a la inversa en general. Por otro lado, para\( i \in I \), vamos\( \mathscr S_i = \{A \in \mathscr S: A \subseteq A_i\} \). Entonces\( \mathscr S_i \) es un\( \sigma \) -álgebra de subconjuntos de\( A_i \) y\( \mu \) restringido a\( \mathscr S_i \) es una medida finita. El punto de esto (y la razón de la definición) es que a menudo las propiedades agradables de las medidas finitas se pueden extender a medidas\( \sigma \) -finitas. En particular, los espacios\( \sigma \) de medida finita juegan un papel crucial en la construcción de espacios de medida de producto, y para la finalización de un espacio de medida considerado a continuación.
Supongamos que\( (S, \mathscr S, \mu) \) es un espacio de medida\( \sigma \) -finito.
- Existe una secuencia creciente que satisface la definición\( \sigma \) finita
- Existe una secuencia disjunta que satisface la definición\( \sigma \) -finita.
Prueba
Sin pérdida de generalidad, podemos tomar\(\N_+\) como el índice establecido en la definición. Entonces existe\( A_n \in \mathscr S\) para\(n \in \N_+ \) tal que\( \mu(A_n) \lt \infty \) para cada uno\( n \in \N_+ \) y\( S = \bigcup_{n=1}^\infty A_n \). La prueba utiliza algunos de los mismos trucos que hemos visto antes.
- Vamos\( B_n = \bigcup_{i = 1}^n A_i \). Entonces\( B_n \in \mathscr S \) para\( n \in \N_+ \) y esta secuencia va en aumento. Además,\( \mu(B_n) \le \sum_{i=1}^n \mu(A_i) \lt \infty \) para\( n \in \N_+ \) y\( \bigcup_{n=1}^\infty B_n = \bigcup_{n=1}^\infty A_n = S \).
- Dejar\( C_1 = A_1 \) y dejar\( C_n = A_n \setminus \bigcup_{i=1}^{n-1} A_i \) para\( n \in \{2, 3, \ldots\} \). Entonces\( C_n \in \mathscr S \) para cada uno\( n \in \N_+ \) y esta secuencia es disjunta. Además,\( C_n \subseteq A_n \) así\( \mu(C_n) \le \mu(A_n) \lt \infty \) y\( \bigcup_{n=1}^\infty C_n = \bigcup_{n=1}^\infty A_n = S \).
Nuestra siguiente definición se refiere a conjuntos donde se concentra una medida, en cierto sentido.
Supongamos que\((S, \mathscr S, \mu)\) es un espacio de medida. Un átomo del espacio es un conjunto\(A \in \mathscr S\) con las siguientes propiedades:
- \(\mu(A) \gt 0\)
- Si\(B \in \mathscr S\) y\(B \subseteq A\) entonces cualquiera\(\mu(B) = \mu(A)\) o\(\mu(B) = 0\).
Un espacio de medida que no tiene átomos se llama no atómico o difuso.
En la teoría de la probabilidad, a menudo nos interesan particularmente los átomos que son conjuntos singleton. Obsérvese que\( \{x\} \in \mathscr S \) es un átomo si y sólo si\( \mu(\{x\}) \gt 0 \), ya que los únicos subconjuntos de\( \{x\} \) son\( \{x\} \) en sí mismos y\( \emptyset \).
Construcciones
Existen varias formas sencillas de construir nuevas medidas positivas a partir de las existentes. Como es habitual, comenzamos con un espacio medible\( (S, \mathscr S) \).
Supongamos que\( (R, \mathscr R) \) es un subespacio medible de\( (S, \mathscr S) \). Si\( \mu \) es una medida positiva en\( (S, \mathscr S) \) entonces\( \mu \) restringida a\( \mathscr R \) es una medida positiva en\( (R, \mathscr R) \). Si\( \mu \) es una medida finita en\( (S, \mathscr S) \) entonces\( \mu \) es una medida finita en\( (R, \mathscr R) \).
Prueba
El supuesto es que\( \mathscr R \) es un\( \sigma \) -álgebra de subconjuntos de\( R \) y\( \mathscr R \subseteq \mathscr S \). En particular\( R \in \mathscr S \). Dado que la propiedad de aditividad de\( \mu \) bodegas para un recuento, colección disjunta de eventos en\( \mathscr S \), se sostiene trivialmente para un recuento, colección disjunta de eventos en\( \mathscr R \). Por último, por el aumento de la propiedad,\( \mu(R) \le \mu(S) \) así que si\( \mu(S) \lt \infty \) entonces\( \mu(R) \lt \infty \).
Sin embargo, si\(\mu\) es\(\sigma\) -finito encendido\( (S, \mathscr S) \), no es necesariamente cierto que\(\mu\) es\(\sigma\) -finito on\( (R, \mathscr R) \). A continuación se da un contraejemplo. El teorema anterior se aplicaría, en particular, cuando\( R = S \) así\( \mathscr R \) es un sub\( \sigma \) -álgebra de\( \mathscr S \). A continuación, un múltiplo positivo de una medida positiva da otra medida positiva.
Si\( \mu \) es una medida positiva sobre\( (S, \mathscr S) \) y\( c \in (0, \infty) \), entonces también\( c \mu \) es una medida positiva sobre\( (S, \mathscr S) \). Si\( \mu \) es finito (\( \sigma \)-finito) entonces\( c \mu \) es finito (\( \sigma \)-finito) respectivamente.
Prueba
Claramente\( c \mu: \mathscr S \to [0, \infty] \). También\( (c \mu)(\emptyset) = c \mu(\emptyset) = 0 \). Siguiente si\( \{A_i: i \in I\} \) es una colección contable, disjunta de eventos en\( \mathscr S \) entonces\[ (c \mu)\left(\bigcup_{i \in I} A_i\right) = c \mu\left(\bigcup_{i \in I} A_i\right) = c \sum_{i \in I} \mu(A_i) = \sum_{i \in I} c \mu(A_i) \] Finalmente, ya que\( \mu(A) \lt \infty \) si y solo si es\( (c \mu)(A) \lt \infty \) para\( A \in \mathscr S \), las propiedades de finitud y\( \sigma \) -finitud se conservan trivialmente.
Una medida positiva finita no trivial\( \mu \) es prácticamente igual que una medida de probabilidad, y de hecho se puede volver a escalar en una medida de probabilidad\( \P \), como se hizo en la sección sobre Medidas de probabilidad:
Supongamos que\( \mu \) es una medida positiva\( (S, \mathscr S) \) con\( 0 \lt \mu(S) \lt \infty \). Entonces\( \P \) definido por\( \P(A) = \mu(A) / \mu(S) \) for\( A \in \mathscr S \) es una medida de probabilidad en\( (S, \mathscr S) \).
Prueba
\( \P \)es una medida por el resultado anterior, y trivialmente\( \P(S) = 1 \).
Las sumas de medidas positivas también son medidas positivas.
Si\( \mu_i \) es una medida positiva\( (S, \mathscr S) \) para cada uno\( i \) en un conjunto de índices contables\( I \) entonces también\( \mu = \sum_{i \in I} \mu_i \) es una medida positiva en\( (S, \mathscr S) \).
- Si\( I \) es finito y\( \mu_i \) es finito para cada uno\(i \in I\) entonces\(\mu\) es finito.
- Si\( I \) es finito y\(\mu_i\) es\( \sigma \) -finito para cada uno\( i \in I \) entonces\( \mu \) es\( \sigma \) -finito.
Prueba
Claramente\( \mu: \mathscr S \to [0, \infty] \). Primero\( \mu(\emptyset) = \sum_{i \in I} \mu_i(\emptyset) = 0 \). Siguiente si\( \{A_j: j \in J\} \) es una colección contable, disjunta de eventos en\( \mathscr S \) entonces\[ \mu\left(\bigcup_{j \in J} A_j\right) = \sum_{i \in I} \mu_i \left(\bigcup_{j \in J} A_j\right) = \sum_{i \in I} \sum_{j \in J} \mu_i(A_j) = \sum_{j \in J} \sum_{i \in I} \mu_i(A_j) = \sum_{j \in J} \mu(A_j) \] El intercambio de sumas es permisible ya que los términos son no negativos. Supongamos ahora que\( I \) es finito.
- Si\( \mu_i \) es finito para cada\( i \in I \) entonces\( \mu(S) = \sum_{i \in I} \mu_i(S) \lt \infty \) entonces\( \mu \) es finito.
- Supongamos que\( \mu_i \) es\( \sigma \) -finito para cada uno\( i \in I \). Entonces para cada uno\( i \in I \) existe una colección\( \mathscr A_i = \{A_{i j}: j \in \N\} \subseteq \mathscr S \) tal que\( \bigcup_{j=1}^\infty A_{i j} = S \) y\( \mu_i(A_{i j}) \lt \infty \) para cada uno\( j \in \N \). Para\( j \in \N \), vamos\( B_j = \bigcap_{i \in I} A_{i,j} \). Entonces\( B_j \in \mathscr S \) para cada uno\( j \in \N \) y\[ \bigcup_{j=1}^\infty B_j = \bigcup_{j=1}^\infty \bigcap_{i \in I} A_{i j} = \bigcap_{i \in I} \bigcup_{j=1}^\infty A_{i j} = \bigcap_{i \in I} S = S \] Por otra parte,\[ \mu(B_j) = \sum_{i \in I} \mu_i(B_j) \le \sum_{i \in I} \mu_i(A_{i j}) \lt \infty \] así\( \mu \) es\( \sigma \) -finnite.
En el contexto del último resultado, si\(I\) es contablemente infinito y\(\mu_i\) es finito para cada uno\(i \in I\), entonces no\(\mu\) es necesariamente\(\sigma\) -finito. A continuación se da un contraejemplo. En este caso,\(\mu\) se dice que es \(s\)-finito, pero ya hemos tenido suficientes definiciones, así que no vamos a perseguir esta. A partir de las propiedades de escala y suma, observe que una combinación lineal positiva de medidas positivas es una medida positiva. El siguiente método a veces se refiere como un cambio de variables.
Supongamos que\( (S, \mathscr S, \mu) \) es un espacio de medida. Supongamos también que\( (T, \mathscr T) \) es otro espacio medible y que\( f: S \to T \) es medible. Luego\( \nu \) se define de la siguiente manera una medida positiva en\( (T, \mathscr T) \)\[ \nu(B) = \mu\left[f^{-1}(B)\right], \quad B \in \mathscr T \] Si\( \mu \) es finita entonces\( \nu \) es finita.
Prueba
Claramente\(\nu: \mathscr T \to [0, \infty]\). La prueba es fácil ya que las imágenes inversas conservan todas las operaciones establecidas. Primero\( f^{-1}(\emptyset) = \emptyset \) así\( \nu(\emptyset) = 0 \). A continuación, si\( \left\{B_i: i \in I\right\} \) es una colección contable, disjunta de conjuntos en\( \mathscr T \), entonces\( \left\{f^{-1}(B_i): i \in I\right\} \) es una colección contable, disjunta de conjuntos en\( \mathscr S \), y\( f^{-1}\left(\bigcup_{i \in I} B_i\right) = \bigcup_{i \in I} f^{-1}(B_i) \). De ahí que\[ \nu\left(\bigcup_{i \in I} B_i\right) = \mu\left[f^{-1}\left(\bigcup_{i \in I} B_i\right)\right] = \mu\left[\bigcup_{i \in I} f^{-1}(B_i)\right] = \sum_{i \in I} \mu\left[f^{-1}(B_i)\right] = \sum_{i \in I} \nu(B_i) \] finalmente, si\(\mu\) es finito entonces\(\nu(T) = \mu[f^{-1}(T)] = \mu(S) \lt \infty\) así\(\nu\) es finito.
En el contexto del último resultado, si\(\mu\) es\(\sigma\) -finito on\((S, \mathscr S)\), no es necesariamente cierto que\(\nu\) es\(\sigma\) -finito on\((T, \mathscr T)\), aunque\(f\) sea uno-a-uno. A continuación se da un contraejemplo. La conclusión es que\(\sigma\) -finitud de\(\nu\) depende en gran medida de la naturaleza de la\(\sigma\) -álgebra\(\mathscr T\). Nuestro siguiente resultado muestra que es fácil construir explícitamente una medida positiva en un \( \sigma \)álgebra generada contablemente, es decir, un\( \sigma \) álgebra generada por una partición contable. Tales\( \sigma \) álgebras son importantes para los contraejemplos y para obtener conocimiento, y también porque muchos\( \sigma \) -álgebras que ocurren en las aplicaciones se pueden construir a partir de ellos.
Supongamos que\( \mathscr A = \{A_i: i \in I\} \) es una partición contable de\( S \) en conjuntos no vacíos, y eso\( \mathscr S = \sigma(\mathscr{A}) \), la\( \sigma \) -álgebra generada por la partición. Para\( i \in I \), definir\( \mu(A_i) \in [0, \infty] \) arbitrariamente. Para\( A = \bigcup_{j \in J} A_j \) dónde\( J \subseteq I \), definir\[ \mu(A) = \sum_{j \in J} \mu(A_j) \] Entonces\( \mu \) es una medida positiva sobre\( (S, \mathscr S) \).
- Los átomos de la medida son los conjuntos de la forma\(A = \bigcup_{j \in J} A_j\) donde\(J \subseteq I\) y donde\(\mu(A_j) \gt 0\) para uno y solo uno\(j \in J\).
- Si\(\mu(A_i) \lt \infty\) for\(i \in I\) y\(I\) es finito entonces\(\mu\) es finito.
- Si\(\mu(A_i) \lt \infty\) for\(i \in I\) y\(I\) es contablemente infinito entonces\(\mu\) es\(\sigma\) -finito.
Prueba
Recordemos que cada uno\( A \in \mathscr S \) tiene una representación única de la forma\( A = \bigcup_{j \in J} A_j \) donde\( J \subseteq I \). En particular,\( J = \emptyset \) en esta representación da\( A = \emptyset \). La suma sobre un conjunto de índices vacíos es 0, entonces\( \mu(\emptyset) = 0 \). A continuación supongamos que\( \{B_k: k \in K\} \) es una colección contable y disjunta de conjuntos en\( \mathscr S \). Entonces existe una colección disjunta\(\{J_k: k \in K\}\) de subconjuntos de\(I\) tales que\( B_k = \bigcup_{j \in J_k} A_j \). De ahí que\[ \mu\left(\bigcup_{k \in K} B_k\right) = \mu\left(\bigcup_{k \in K} \bigcup_{j \in J_k} A_j\right) = \sum_{k \in k}\sum_{j \in J_k} \mu(A_j) = \sum_{k \in K} \mu(B_k) \] el hecho de que los términos sean todos no negativos significa que no tenemos que preocuparnos por el orden de la suma.
- Nuevamente, cada uno\(A \in \mathscr S\) tiene la representación única\(A = \bigcup_{j \in J} A_j\) donde\(J \subseteq I\). Los subconjuntos de\(A\) eso están adentro\(\mathscr S\)\(\bigcup_{k \in K} A_k\) están aquí\(K \subseteq J\). De ahí\(A\) que sea un átomo si y sólo si\(\mu(A_j) \gt 0\) para uno y solo uno\(j \in J\).
- Si\(I\) es finito y\(\mu(A_i) \lt \infty\) entonces\(\mu(S) = \sum_{i \in I} \mu(A_i) \lt \infty\), así\(\mu\) es finito.
- Si\(I\) es infinitamente contable y\(\mu(A_i) \lt \infty\) para\(i \in I\) entonces\(\mathscr A\) satisface la condición\(\mu\) para ser\(\sigma\) -finito.
Una de las formas más generales de construir nuevas medidas a partir de las antiguas es a través de la teoría de la integración con respecto a una medida positiva, la cual se explora en el capítulo sobre Distribuciones. La construcción de medidas positivas más o menos desde cero
se considera en la siguiente sección sobre Existencia y Singularidad. Cerramos esta discusión con un resultado simple que es útil para contraejemplos.
Supongamos que el espacio de medida\( (S, \mathscr S, \mu) \) tiene un átomo\( A \in \mathscr S \) con\( \mu(A) = \infty \). Entonces el espacio no es\( \sigma \) -finito.
Prueba
Dejar\( \{A_i: i \in I\} \) ser una colección disjunta contable de conjuntos en\( \mathscr S \) esas particiones\( S \). Después\( \{A \cap A_i: i \in I\} \) particiones\( A \). Ya que\( \mu(A) = \sum_{i \in I} \mu(A \cap A_i) \), debemos tener\( \mu(A \cap A_i) \gt 0 \) para algunos\( i \in I \). Ya que\( A \) es un átomo y de\( A \cap A_i \subseteq A \) ello se deduce\( \mu(A \cap A_i) = \infty \). De ahí también por lo tanto\( \mu(A_i) = \infty \).
Medida y Topología
A menudo los espacios que ocurren en probabilidad y procesos estocásticos son espacios topológicos. Recordemos que un espacio topológico\( (S, \mathscr T) \) consiste en un conjunto\( S \) y una topología\( \mathscr T \) on\( S \) (la colección de conjuntos abiertos). Tanto la topología como la teoría de medidas juegan un papel importante, por lo que es natural querer que estos dos tipos de estructuras sean compatibles. Ya hemos visto el paso más importante en esta dirección: Recordemos que\( \mathscr S = \sigma(\mathscr T) \), la\( \sigma \) -álgebra generada por la topología, es la \( \sigma \)-álgebra de Borel on\( S \), llamada así por Émile Borel. Dado que el complemento de un conjunto abierto es un conjunto cerrado, también\(\mathscr S\) es la\(\sigma\) -álgebra generada por la colección de conjuntos cerrados. Además,\(\mathscr S\) contiene intersecciones contables de conjuntos abiertos (llamados \(G_\delta\)conjuntos) y uniones contables de conjuntos cerrados (llamados \(F_\sigma\)conjuntos).
Supongamos que\( (S, \mathscr T) \) es un espacio topológico y deja\(\mathscr S = \sigma(\mathscr T)\) ser el\(\sigma\) álgebra de Borel. Una medida\( \mu \) positiva\( (S, \mathscr S) \) es una medida de Borel y luego\((S, \mathscr S, \mu)\) es un espacio de medida de Borel.
La siguiente definición se refiere al subconjunto en el que se concentra una medida de Borel, en cierto sentido.
Supongamos que\((S, \mathscr S, \mu)\) es un espacio de medida de Borel. El soporte de\(\mu\) es\[\supp(\mu) = \{x \in S: \mu(U) \gt 0 \text{ for every open neighborhood } U \text{ of } x\}\] El conjunto\(\supp(\mu)\) está cerrado.
Prueba
Vamos\(A = \supp(\mu)\). Porque\(x \in A^c\), existe un barrio abierto\(V_x\) de\(x\) tal que\(\mu(V_x) = 0\). Si\(y \in V_x\), entonces también\(V_x\) es un barrio abierto de\(y\), entonces\(y \in A^c\). De ahí que\(V_x \subseteq A^c\) para cada\(x \in A^c\) y así\( A^c \) esté abierto.
El término medida de Borel tiene diferentes definiciones en la literatura. A menudo se requiere que el espacio topológico sea localmente compacto, Hausdorff, y con una base contable (LCCB). Entonces\( \mu \) se requiere una medida Borel para tener la condición adicional que\( \mu(C) \lt \infty \) si\( C \subseteq S \) es compacta. En este texto, utilizamos el término medidas de Borel en este sentido más restringido.
Supongamos que\((S, \mathscr S, \mu)\) es un espacio de medida de Borel correspondiente a una topolgia LCCB. Entonces el espacio es\(\sigma\) -finito.
Prueba
Dado que el espacio topológico es localmente compacto y tiene una base contable,\(S = \bigcup_{i \in I} C_i\) donde\(\{C_i: i \in I\}\) se encuentra una colección contable de conjuntos compactos. Dado que\(\mu\) es una medida Borel,\(\mu(C_i) \lt \infty\) y por lo tanto\(\mu\) es\(\sigma\) -finita.
Aquí hay un par de otras definiciones que son importantes para las medidas de Borel, nuevamente vinculando la topología y la medida de manera natural.
Supongamos nuevamente que\( (S, \mathscr S, \mu) \) es un espacio de medida de Borel.
- \( \mu \)es regular interior si es\( \mu(A) = \sup\{\mu(C): C \text{ is compact and } C \subseteq A\} \) para\( A \in \mathscr S \).
- \( \mu \)es regular exterior si es\( \mu(A) = \inf\{\mu(U): U \text{ is open and } A \subseteq U\} \) para\( A \in \mathscr S \).
- \( \mu \)es regular si es regular tanto interior como regular exterior.
Los espacios de medida que ocurren en probabilidad y procesos estocásticos suelen ser espacios Borel regulares asociados con topologías LCCB.
Conjuntos nulos y equivalencia
Los conjuntos de medida 0 en un espacio de medida resultan ser muy importantes precisamente porque a menudo podemos ignorar las diferencias entre objetos matemáticos en dichos conjuntos. En esta disusión, asumimos que tenemos un espacio de medida fija\((S, \mathscr S, \mu)\).
Un conjunto\(A \in \mathscr S\) es nulo si\(\mu(A) = 0\).
Considera una declaración
medible con\( x \in S \) como variable libre. (Técnicamente, tal declaración es un predicado sobre\( S \).) Si la declaración es verdadera para todos\( x \in S \) excepto para\( x \) en un conjunto nulo, decimos que la declaración se mantiene en casi todas partes encendida\( S \). Esta terminología se utiliza a menudo en la teoría de medidas y captura la importancia de la definición.
Let\( \mathscr D = \{A \in \mathscr S: \mu(A) = 0 \text{ or } \mu(A^c) = 0\}\), la colección de conjuntos nulos y co-nulos. Entonces\( \mathscr D \) es un sub\(\sigma\) -álgebra de\( \mathscr S \).
Prueba
Trivialmente\( S \in \mathscr D \) desde\(S^c = \emptyset\) y\(\mu(\emptyset) = 0\). Siguiente si\(A \in \mathscr D\) entonces\(A^c \in \mathscr D\) por la simetría de la definición. Por último, supongamos que\( A_i \in \mathscr D \) para\( i \in I \) donde\( I \) es un conjunto de índices contables. Si\( \mu(A_i) = 0 \) por cada\( i \in I \) entonces\( \mu\left(\bigcup_{i \in I} A_i \right) \le \sum_{i \in I} \mu(A_i) = 0 \) por la propiedad subaditiva. Por otro lado, si\( \mu(A_j^c) = 0 \) para algunos\( j \in J \) entonces\( \mu\left[\left(\bigcup_{i \in I} A_i \right)^c\right] = \mu\left(\bigcap_{i \in I} A_i^c\right) \le \mu(A_j^c) = 0 \). En cualquier caso,\( \bigcup_{i \in I} A_i \in \mathscr D \).
Por supuesto\(\mu\) restringido a no\(\mathscr D\) es muy interesante desde\(\mu(A) = 0\) o\(\mu(A) = \mu(S)\) para todos\(A \in \mathscr S\). Nuestra siguiente definición es un tipo de equivalencia entre conjuntos en\(\mathscr S\). Para hacer esto preciso, recordemos primero que la diferencia simétrica entre los subconjuntos\( A \) y\( B \) de\(S\) es\( A \bigtriangleup B = (A \setminus B) \cup (B \setminus A) \). Este es el conjunto que consta de puntos en uno de los dos conjuntos, pero no ambos, y corresponde a exclusivo o.
\(A, \, B \in \mathscr S\)Los conjuntos son equivalentes si\(\mu(A \bigtriangleup B) = 0 \), y denotamos esto por\( A \equiv B \).
Así\(A \equiv B\) si y sólo si y sólo\(\mu(A \bigtriangleup B) = \mu(A \setminus B) + \mu(B \setminus A) = 0\) si y sólo si\(\mu(A \setminus B) = \mu(B \setminus A) = 0\). En la terminología predicada antes mencionada, la afirmación\[ x \in A \text{ if and only if } x \in B \] es cierta para casi todos\( x \in S \). Como su nombre indica, la relación\( \equiv \) realmente es una relación de equivalencia\( \mathscr S \) y, por lo tanto,\( \mathscr S \) se divide en clases disjuntas de conjuntos mutuamente equivalentes. Dos conjuntos en la misma clase de equivalencia difieren en un conjunto de medida 0.
La relación\( \equiv \) es una relación de equivalencia sobre\( \mathscr S \). Es decir, para\( A, \, B, \, C \in \mathscr S \),
- \(A \equiv A\)(la propiedad reflexiva).
- Si\(A \equiv B\) entonces\(B \equiv A\) (la propiedad simétrica).
- Si\(A \equiv B\) y\(B \equiv C\) entonces\(A \equiv C\) (la propiedad transitiva).
Prueba
- La propiedad reflexiva es trivial desde entonces\(A \bigtriangleup A = \emptyset\).
- La propiedad simétrica también es trivial desde entonces\(A \bigtriangleup B = B \bigtriangleup A\).
- Para la propiedad transitiva, supongamos que\( A \equiv B \) y\( B \equiv C \). Tenga en cuenta que\( A \setminus C \subseteq (A \setminus B) \cup (B \setminus C) \), y por lo tanto\( \P(A \setminus C) = 0 \). Por un argumento simétrico,\( \P(C \setminus A) = 0 \).
La equivalencia se conserva bajo las operaciones estándar establecidas.
Si\( A, \, B \in \mathscr S \) y\( A \equiv B \) entonces\( A^c \equiv B^c \).
Prueba
Tenga en cuenta que\( A^c \setminus B^c = B \setminus A \) y\( B^c \setminus A^c = A \setminus B \), entonces\( A^c \bigtriangleup B^c = A \bigtriangleup B \).
Supongamos que\( A_i, \, B_i \in \mathscr S \) y eso\( A_i \equiv B_i \) para\( i \) en un conjunto de índices contables\( I \). Entonces
- \( \bigcup_{i \in I} A_i \equiv \bigcup_{i \in I} B_i \)
- \( \bigcap_{i \in I} A_i \equiv \bigcap_{i \in I} B_i \)
Prueba
- Tenga en cuenta que\[ \left(\bigcup_{i \in I} A_i\right) \bigtriangleup \left(\bigcup_{i \in I} B_i\right) \subseteq \bigcup_{i \in I} (A_i \bigtriangleup B_i) \] Para ver esto, tenga en cuenta que si\( x \) está en el set de la izquierda entonces ya sea\( x \in A_j \) para algunos\( j \in I \) y\( x \notin B_i \) para todos\( i \in I \), o\( x \notin A_i \) para todos\( i \in I \) y\( x \in B_j \) para algunos\( j \in I \). En cualquier caso,\( x \in A_j \bigtriangleup B_j \) para algunos\( j \in I \).
- De igual manera\[ \left(\bigcap_{i \in I} A_i\right) \bigtriangleup \left(\bigcap_{i \in I} B_i\right) \subseteq \bigcup_{i \in I} (A_i \bigtriangleup B_i) \] Si\( x \) está en el set de la izquierda entonces\( x \in A_i \) para todos\( i \in I \) y\( x \notin B_j \) para algunos\( j \in I \), o\( x \in B_i \) para todos\( i \in I \) o\( x \notin A_j \) para algunos\( j \in I \). En cualquier caso,\( x \in A_j \bigtriangleup B_j \) para algunos\( j \in I \)
En ambas partes, la prueba se completa señalando que el conjunto común a la derecha en las ecuaciones mostradas es nulo:\[ \mu\left[\bigcup_{i \in I} (A_i \bigtriangleup B_i) \right] \le \sum_{i \in I} \mu(A_i \bigtriangleup B_i) = 0 \]
Los conjuntos equivalentes tienen la misma medida.
Si\( A, \, B \in \mathscr S \) y\(A \equiv B\) entonces\(\mu(A) = \mu(B)\).
Prueba
Tenga en cuenta de nuevo eso\( A = (A \cap B) \cup (A \setminus B) \). Si\( A \equiv B \) entonces\( \mu(A) = \mu(A \cap B) \). Por un argumento simétrico,\( \mu(B) = \mu(A \cap B) \).
Lo contrario falla trivialmente, y a continuación se da un contraejemplo. Sin embargo, la colección de conjuntos nulos y la colección de conjuntos co-nulos forman clases de equivalencia.
Supongamos que\( A \in \mathscr S \).
- Si\(\mu(A) = 0\) entonces\(A \equiv B\) si y solo si\(\mu(B) = 0\).
- Si\(\mu(A^c) = 0\) entonces\(A \equiv B\) si y solo si\(\mu(B^c) = 0\).
Prueba
- Supongamos que\( \mu(A) = 0 \) y\( A \equiv B\). Entonces\( \mu(B) = 0 \) por el resultado anterior. Por el contrario, tenga en cuenta eso\( A \setminus B \subseteq A \) y\( B \setminus A \subseteq B \) así si\( \mu(A) = \mu(B) = 0 \) entonces\( \mu(A \bigtriangleup B) = 0 \) es así\( A \equiv B \).
- La parte b) se desprende de la parte a) y el resultado anterior sobre los complementos.
Podemos extender la noción de equivalencia a funciones mensurables con un espacio de alcance común. Así supongamos que\( (T, \mathscr T) \) es otro espacio medible. Si\( f, \, g: S \to T \) son medibles, entonces\( (f, g): S \to T \times T \) es medible con respecto al producto habitual\( \sigma \) -álgebra\( \mathscr T \otimes \mathscr T \). Suponemos que el conjunto diagonal\( D = \{(y, y): y \in T\} \in \mathscr T \otimes \mathscr T \), que casi siempre es cierto en las aplicaciones.
Las funciones medibles\(f, \, g: S \to T\) son equivalentes si\( \mu\{x \in S: f(x) \ne g(x)\} = 0 \). Nuevamente escribimos\( f \equiv g \).
Detalles
Tenga en cuenta que\(\{x \in S: f(x) \ne g(x)\} = \{x \in S: (f(x), g(x)) \in D\}^c \in \mathscr S\) por nuestra suposición, por lo que la definición tiene sentido.
En la terminología discutida anteriormente,\( f \equiv g \) significa que\( f(x) = g(x) \) casi en todas partes en\( S \). Al igual que con los conjuntos medibles, la relación\( \equiv \) realmente define una relación de equivalencia en la colección de funciones medibles desde\(S\) hasta\(T\). Así, la colección de tales funciones se divide en clases disjuntas de variables mutuamente equivalentes.
La relación\( \equiv \) es una relación de equivalencia sobre la colección de funciones medibles desde\(S\) hasta\(T\). Es decir, para medible\(f, \, g, \, h: S \to T\),
- \(f \equiv f\)(la propiedad reflexiva).
- Si\(f \equiv g\) entonces\(g \equiv f\) (la propiedad simétrica).
- Si\( f \equiv g\) y\(g \equiv h\) entonces\(f \equiv h\) (la propiedad transitiva).
Prueba
Las partes (a) y (b) son trivialmente. Para (c) señalar que\( f(x) = g(x) \) e\( g(x) = h(x) \) implica\( f(x) = h(x) \) para\( x \in S \). Negar esta afirmación da\( f(x) \ne h(x) \) implica\( f(x) \ne g(x) \) o\( g(x) \ne h(x) \). Entonces\[ \{x \in S: f(x) \ne h(x)\} \subseteq \{x \in S: f(x) \ne g(x)\} \cup \{ x \in S: g(x) \ne h(x)\} \] Desde\( f \equiv g \) y\( g \equiv h \), los dos sets de la derecha tienen medida 0. De ahí que también lo haga el set de la izquierda.
Supongamos agaom que\(f, \, g: S \to T\) son medibles y eso\(f \equiv g\). Entonces para cada\(B \in \mathscr T\), los sets\(f^{-1}(B) \equiv g^{-1}(B)\).
Prueba
Tenga en cuenta que\( f^{-1}(B) \bigtriangleup g^{-1}(B) \subseteq \{x \in S: f(x) \ne g(x)\} \).
Así si\( f, \, g: S \to T \) son medibles y\( f \equiv g \), entonces por el resultado anterior,\(\nu_f = \nu_g\) donde\(\nu_f, \, \nu_g\) están las medidas en\((T, \mathscr T)\) asociadas con\( f \) y\( g \), como arriba. Nuevamente, lo contrario falla con pasión.
A menudo sucede que una definición de funciones subsume la definición correspondiente para conjuntos, al considerar las funciones indicadoras de los conjuntos. Así es con equivalencia. En el siguiente resultado, podemos tomar\(T = \{0, 1\}\) con\(\mathscr T\) la colección de todos los subconjuntos.
Supongamos que\(A, \, B \in \mathscr S\). Entonces\(A \equiv B\) si y sólo si\(\bs{1}_A \equiv \bs{1}_B\).
Prueba
Tenga en cuenta que\( \left\{x \in S: \bs{1}_A(x) \ne \bs{1}_B(x) \right\} = A \bigtriangleup B \).
La equivalencia se conserva bajo composición. Para el siguiente resultado, supongamos que ese\((U, \mathscr U)\) es otro espacio medible más.
Supongamos que\(f, \, g: S \to T\) son medibles y eso\(h: T \to U\) es medible. Si\(f \equiv g\) entonces\(h \circ f \equiv h \circ g\).
Prueba
Tenga en cuenta que\( \{x \in S: h[f(x)] \ne h[g(x)]\} \subseteq \{x \in S: f(x) \ne g(x)\} \).
Supongamos nuevamente que\( (S, \mathscr S, \mu) \) es un espacio de medida. Let\( \mathscr V \) denotar la colección de todas las funciones aleatorias de valor real medibles desde\( S \) dentro\( \R \). (Como de costumbre,\(\R\) se le da el\(\sigma\) álgebra de Borel.) De nuestra anterior discusión sobre la teoría de medidas, sabemos que con las definiciones habituales de suma y multiplicación escalar,\( (\mathscr V, +, \cdot) \) es un espacio vectorial. Sin embargo, en la teoría de medidas, muchas veces no queremos distinguir entre funciones que son equivalentes, por lo que es bueno saber que la estructura del espacio vectorial se conserva cuando identificamos funciones equivalentes. Formalmente, vamos a\( [f] \) denotar la clase de equivalencia generada por\( f \in \mathscr V \), y dejar\( \mathscr W \) denotar la colección de todas esas clases de equivalencia. En notación modular,\( \mathscr W\) es\(\mathscr V \big/ \equiv \). Definimos suma y multiplicación escalar en\( \mathscr W \) por\[ [f] + [g] = [f + g], \; c [f] = [c f]; \quad f, \, g \in \mathscr V, \; c \in \R \]
\( (\mathscr W, +, \cdot) \)es un espacio vectorial.
Prueba
Todo lo que tenemos que mostrar es que la suma y la multiplicación escalar están bien definidas. Es decir, debemos demostrar que las definiciones no dependen de lo particularmente representativo de la clase de equivalencia. Entonces se heredan de las otras propiedades que definen un espacio vectorial\( (\mathscr V, +, \cdot) \). Así debemos demostrar que si\( f_1 \equiv f_2 \) y\( g_1 \equiv g_2 \), y si\( c \in \R \), entonces\( f_1 + g_1 \equiv f_2 + g_2 \) y\( c f_1 \equiv c f_2 \). Para el primer problema, tenga en cuenta que\((f_1, g_1)\) y\((f_2, g_2)\) son funciones medibles desde\(S\) hasta\(\R^2\). (\(\R^2\)se le da el producto\(\sigma\) -álgebra que también pasa a ser el\(\sigma\) álgebra de Borel correspondiente a la topolgia euclidiana estándar). Además,\((f_1, g_1) \equiv (f_2, g_2)\) ya que\[\{x \in S: (f_1(x), g_1(x)) \ne (f_2(x), g_2(x))\} = \{x \in S: f_1(x) \ne f_2(x)\} \cup \{x \in S: g_1(x) \ne g_2(x)\}\] Pero la función\((a, b) \mapsto a + b\) de\(\R^2\) hacia dentro\(\R\) es medible y por lo tanto de propiedad de composición, se deduce de eso\(f_1 + g_1 \equiv f_2 + g_2\). El segundo problema es más fácil. La función\(a \mapsto c a\) de\(\R\) dentro\(\R\) es medible así que de nuevo se follos de la propiedad de composición que\(c f_1 \equiv c f_2\).
A menudo no nos molestamos en usar la notación especial para la clase de equivalencia asociada a una función. Más bien, se entiende que las funciones equivalentes representan el mismo objeto. Los espacios de funciones en un espacio de medida se estudian más a fondo en el capítulo Distribuciones.
Finalización
Supongamos que\( (S, \mathscr S, \mu) \) es un espacio de medida y vamos a\( \mathscr N = \{A \in \mathscr S: \mu(A) = 0\} \) denotar la colección de conjuntos nulos del espacio. Si\( A \in \mathscr N \) y\( B \in \mathscr S \) es un subconjunto de\( A \), entonces sabemos que\( \mu(B) = 0 \) así\( B \in \mathscr N \) también. No obstante, en general podría haber subconjuntos de los\( A \) que no están en\( \mathscr S \). Esto lleva naturalmente a la siguiente definición.
El espacio de medida\( (S, \mathscr S, \mu) \) es completo si\( A \in \mathscr N \) e\( B \subseteq A \) implica\( B \in \mathscr S \) (y por lo tanto\( B \in \mathscr N \)).
Nuestro objetivo en esta discusión es mostrar que si\( (S, \mathscr S, \mu) \) es una medida\( \sigma \) -finita que no está completa, entonces se puede completar. Es decir, se\( \mu \) puede extender a\( \sigma \) -álgebra que incluye todos los conjuntos en\( \mathscr S \) y todos los subconjuntos de conjuntos nulos. El primer paso es extender la relación de equivalencia definida en nuestra discusión anterior a\( \mathscr P(S) \).
Para\( A, \, B \subseteq S \), definir\( A \equiv B \) si y sólo si existe\( N \in \mathscr N \) tal que\( A \bigtriangleup B \subseteq N \). La relación\( \equiv \) es una relación de equivalencia sobre\( \mathscr{P}(S) \): Por\( A, \, B, \, C \subseteq S \),
- \( A \equiv A \)(la propiedad reflexiva).
- Si\( A \equiv B \) entonces\( B \equiv A \) (la propiedad simétrica).
- Si\( A \equiv B \) y\( B \equiv C \) entonces\( A \equiv C \) (la propiedad transitiva).
Prueba
- Tenga en cuenta que\( A \bigtriangleup A = \emptyset \) y\( \emptyset \in \mathscr N \).
- Supongamos que\( A \bigtriangleup B \subseteq N \) donde\( N \in \mathscr N \). Entonces\( B \bigtriangleup A = A \bigtriangleup B \subseteq N\).
- Supongamos eso\( A \bigtriangleup B \subseteq N_1 \) y\( B \bigtriangleup C \subseteq N_2\) dónde\( N_1, \; N_2 \in \mathscr N \). Entonces\( A \bigtriangleup C \subseteq (A \bigtriangleup B) \cup (B \bigtriangleup C) \subseteq N_1 \cup N_2 \), y\( N_1 \cup N_2 \in \mathscr N \).
Entonces la relación de equivalencia\( \mathscr P(S) \) se\( \equiv \) divide en clases de equivalencia mutuamente disjuntas. Dos conjuntos en una clase de equivalencia difieren por un subconjunto de un conjunto nulo. En particular,\( A \equiv \emptyset \) si y sólo si\( A \subseteq N \) para algunos\( N \in \mathscr N \). La relación extendida\( \equiv \) se conserva bajo las operaciones establecidas, igual que antes. Nuestro siguiente paso es agrandar el\( \sigma \) álgebra\( \mathscr S \) agregando cualquier conjunto que sea equivalente a un conjunto en\( \mathscr S \).
Vamos\( \mathscr S_0 = \{A \subseteq S: A \equiv B \text{ for some } B \in \mathscr S \} \). Entonces\( \mathscr S_0 \) es una\( \sigma \) -álgebra de subconjuntos de\( S \), y de hecho es la\( \sigma \) -álgebra generada por\( \mathscr S \cup \{A \subseteq S: A \equiv \emptyset\} \).
Prueba
Tenga en cuenta que si\( A \in \mathscr S \) entonces\( A \equiv A \) es así\( A \in \mathscr S_0 \). En particular,\( S \in \mathscr S_0 \). También,\( \emptyset \in \mathscr S \) así que si\( A \equiv \emptyset \) entonces\( A \in \mathscr S_0 \). Supongamos\( A \in \mathscr S_0 \) eso\( A \equiv B \) para que para algunos\( B \in \mathscr S \). Entonces\( B^c \in \mathscr S \) y\( A^c \equiv B^c \) así\( A^c \in \mathscr S_0 \). Siguiente supongamos que\( A_i \in \mathscr S_0 \) para\( i \) en un conjunto de índices contables\( I \). Entonces para cada uno\( i \in I \) existe\( B_i \in \mathscr S \) tal que\( A_i \equiv B_i \). Pero entonces\( \bigcup_{i \in I} B_i \in \mathscr S \) y\( \bigcup_{i \in I} A_i \equiv \bigcup_{i \in I} B_i \), entonces\( \bigcup_{i \in I} A_i \in \mathscr S_0 \). Por lo tanto\( \mathscr S_0 \) es un\( \sigma \) -álgebra de subconjuntos de\( S \). Por último, supongamos que\( \mathscr T \) es un\( \sigma \) -álgebra de subconjuntos de\( S \) y eso\( \mathscr S \cup \{A \subseteq S: A \equiv \emptyset\} \subseteq \mathscr T \). Tenemos que demostrarlo\( \mathscr S_0 \subseteq \mathscr T \). Así, supongamos que\( A \in \mathscr S_0 \) Entonces existe\( B \in \mathscr S \) tal que\( A \equiv B \). Pero\( B \in \mathscr T \) y\( A \bigtriangleup B \in \mathscr T \) así\( A \cap B = B \setminus (A \bigtriangleup B) \in \mathscr T\). También\( A \setminus B \in \mathscr T \), entonces\( A = (A \cap B) \cup (A \setminus B) \in \mathscr T \).
Nuestro último paso es extender\( \mu \) a una medida positiva sobre el\( \sigma \) álgebra agrandada\( \mathscr S_0 \).
Supongamos\( A \in \mathscr S_0 \) eso\( A \equiv B \) para que para algunos\( B \in \mathscr S \). Definir\( \mu_0(A) = \mu(B) \). Entonces
- \( \mu_0 \)está bien definido.
- \( \mu_0(A) = \mu(A) \)para\( A \in \mathscr S \).
- \( \mu_0 \)es una medida positiva sobre\( \mathscr S_0 \).
El espacio de medida\( (S, \mathscr S_0, \mu_0) \) está completo y se conoce como la finalización de\( (S, \mathscr S, \mu) \).
Prueba
- Supongamos eso\( A \in \mathscr S_0 \) y\( A \equiv B_1 \) aquello y\( A \equiv B_2 \) dónde\( B_1, \, B_2 \in \mathscr S \). Entonces\(B_1 \equiv B_2 \) así por el resultado anterior\( \mu(B_1) = \mu(B_2) \). Así,\( \mu_0 \) está bien definido.
- Siguiente, si\( A \in \mathscr S \) entonces claro\( A \equiv A \) que así\( \mu_0(A) = \mu(A) \).
- Trivialmente\( \mu_0(A) \ge 0 \) para\( A \in \mathscr S_0 \). Así solo necesitamos mostrar la propiedad de aditividad contable. Para entender la prueba es necesario tener en cuenta varios hechos: las funciones\( \mu \) y\( \mu_0 \) acordar\( \mathscr S \) (propiedad (b)); la equivalencia se conserva bajo operaciones establecidas; conjuntos equivalentes tienen el mismo valor bajo\( \mu_0 \) (propiedad (a)). Dado que el espacio de medida\( (S, \mathscr S, \mu) \) es\( \sigma \) -finito, existe una colección disjunta contable\( \{C_i: i \in I\} \) de conjuntos en\( \mathscr S \) tal que\( S = \bigcup_{i \in I} C_i \) y\( \mu(C_i) \lt \infty \) para cada uno\( i \in I \). Supongamos primero eso\( A \in \mathscr S_0 \), para que exista\( B \in \mathscr S \) con\( A \equiv B \). Entonces\[\mu_0(A) = \mu_0\left[\bigcup_{i \in I} (A \cap C_i)\right] = \mu\left[\bigcup_{i \in I} (B \cap C_i)\right] = \sum_{i \in I} \mu(B \cap C_i) = \sum_{i \in I} \mu_0(A \cap C_i)\] Supongamos siguiente que\( (A_1, A_2, \ldots) \) es una secuencia de conjuntos disjuntos por pares en\( \mathscr S_0 \) para que exista una secuencia\( (B_1, B_2, \ldots) \) de conjuntos en\( \mathscr S \) tal que\( A_i \equiv B_i \) para cada uno\( i \in \N_+ \). Para fijo\( i \in I \),\[ \mu_0\left[\bigcup_{n=1}^\infty (A_n \cap C_i)\right] = \mu_0\left[\bigcup_{n=1}^\infty (B_n \cap C_i)\right] = \mu\left[\bigcup_{n=1}^\infty (B_n \cap C_i)\right] = \sum_{in=1}^\infty \mu(B_n \cap C_i) = \sum_{n=1}^\infty \mu_0(A_n \cap C_i) \] La próxima a la última igualdad usa la ley de inclusión-exclusión, ya que no sabemos (y probablemente no sea cierto) que la secuencia\( (B_1, B_2, \ldots) \) es disjunta. El uso de inclusión-exclusión es por lo\( (S, \mathscr S, \mu) \) que necesitamos ser\( \sigma \) -finitos. Finalmente, usando las ecuaciones mostradas anteriormente,\ begin {align*}\ mu_0\ left (\ bigcup_ {n=1} ^\ infty a_N\ right) & =\ sum_ {i\ in I}\ mu_0\ left [\ left (\ bigcup_ {n=1} ^\ infty a_n\ right)\ cap c_i\ right] =\ sum_ {i\ in I}\ mu_0\ izquierda (\ bigcup_ {n=1} ^\ infty a_n\ cap C_i\ derecha)\\ & =\ sum_ {i\ in I}\ suma_ {n=1} ^\ infty\ mu_0 (a_n\ cap C_i) =\ suma_ {n=1} ^\ infty\ suma_ {i\ en I}\ mu_0 (a_n\ cap C_i) =\ suma_ {n=1} ^\ infty\ mu_0 (a_n)\ end {align*}
Ejemplos y ejercicios
Como siempre, asegúrate de probar los ejercicios computacionales y pruebas antes de leer las respuestas y pruebas en el texto. Recordemos que un espacio de medida discreto consiste en un conjunto contable, con el\( \sigma \) álgebra de todos los subconjuntos, y con la medida de conteo\( \# \).
Contraejemplos
El teorema de continuidad para eventos decrecientes puede fallar si los eventos no tienen medida finita.
Considera\( \Z \) con medida de conteo\( \# \) sobre el\( \sigma \) álgebra de todos los subconjuntos. Dejemos\( A_n = \{ z \in \Z: z \le -n\} \) para\( n \in \N_+ \). El teorema de continuidad falla para\( (A_1, A_2, \ldots) \).
Prueba
La secuencia es decreciente y\( \#(A_n) = \infty \) para cada uno\( n \), pero\( \# \left(\bigcap_{i=1}^\infty A_i\right) = \#(\emptyset) = 0 \).
La igual medida ciertamente no implica conjuntos equivalentes.
Supongamos que\( (S, \mathscr S, \mu) \) es un espacio de medida con la propiedad de que existen conjuntos disjuntos\( A, \, B \in \mathscr S\) tal que\( \mu(A) = \mu(B) \gt 0 \). Entonces\( A \) y no\( B \) son equivalentes.
Prueba
Tenga en cuenta que\( A \bigtriangleup B = A \cup B \) y\( \mu(A \cup B) \gt 0 \).
Para un ejemplo concreto, podríamos tomar\( S = \{0, 1\} \) con el conteo de medidas\( \# \) sobre\( \sigma \) -álgebra de todos los subconjuntos, y\( A = \{0\} \),\( B = \{1\} \).
La propiedad\( \sigma \) -finita no es necesariamente heredada por un espacio de submedida. Para establecer el escenario para el contraejemplo, vamos a\( \mathscr R \) denotar el\( \sigma \) álgebra de Borel de\( \R \), es decir, la\( \sigma \) -álgebra generada por la topología euclidiana estándar. Existe una medida positiva\( \lambda \) sobre\( (\R, \mathscr R) \) que generaliza la longitud. La medida\( \lambda \), conocida como medida Lebesgue, se construye en el apartado de Existencia. A continuación vamos a\( \mathscr C \) denotar el\( \sigma \) -álgebra de conjuntos contables y cocontables:\[ \mathscr C = \{A \subseteq \R: A \text{ is countable or } A^c \text{ is countable}\} \] Eso\( \mathscr C \) es un\( \sigma \) -álgebra se mostró en la sección sobre teoría de medidas en el capítulo sobre fundaciones.
\( (\R, \mathscr C) \)es un subespacio de\( (\R, \mathscr R) \). Además,\( (\R, \mathscr R, \lambda) \) es\( \sigma \) -finito pero no\( (\R, \mathscr C, \lambda) \) lo es.
Prueba
Si\( x \in \R \), entonces el singleton\( \{x\} \) está cerrado y por lo tanto está adentro\( \mathscr R \). Un conjunto contable es una unión contable de singletons, así que si\( A \) es contable entonces\( A \in \mathscr R \). De ello se deduce que\( \mathscr C \subset \mathscr R \). A continuación, vamos a\( I_n \) denotar el intervalo\( [n, n + 1) \) para\( n \in \Z \). Entonces\( \lambda(I_n) = 1 \) para\( n \in Z \) y\( \R = \bigcup_{n \in \Z} I_n \), así\( (\R, \mathscr R, \lambda) \) es\( \sigma \) -finito. Por otro lado,\( \lambda\{x\} = 0 \) for\( x \in R \) (ya que el conjunto es un intervalo de longitud 0). Por lo tanto\( \lambda(A) = 0 \) si\( A \) es contable y\( \lambda(A) = \infty \) si\( A^c \) es contable. De ello se deduce que\( \R \) no se puede escribir como una unión contable de conjuntos en\( \mathscr C \), cada uno con medida finita.
Una suma de medidas finitas puede no ser\( \sigma \) -finita.
Dejar\( S \) ser un conjunto finito no vacío con el\( \sigma \) -álgebra\( \mathscr S \) de todos los subconjuntos. Vamos\( \mu_n = \# \) a contar la medida\( (S, \mathscr S) \) para\( n \in \N_+ \). Entonces\( \mu_n \) es una medida finita para cada uno\( n \in \N_+ \), pero no\( \mu = \sum_{n \in \N_+} \mu_n \) es\( \sigma \) -finita.
Prueba
Tenga en cuenta que\( \mu \) es la medida trivial sobre\( (S, \mathscr S) \) dada por\( \mu(A) = \infty \) if\( A \ne \emptyset \) (y por supuesto\( \mu(\emptyset) = 0 \)).
Propiedades Básicas
En los siguientes problemas,\( \mu \) es una medida positiva sobre el espacio medible\( (S, \mathscr S) \).
Supongamos eso\( \mu(S) = 20 \) y\(A, B \in \mathscr S\) aquello con\(\mu(A) = 5\),\(\mu(B) = 6 \),\(\mu(A \cap B) = 2\). Encuentra la medida de cada uno de los siguientes conjuntos:
- \(A \setminus B\)
- \(A \cup B\)
- \(A^c \cup B^c\)
- \(A^c \cap B^c\)
- \(A \cup B^c\)
Contestar
- 3
- 9
- 18
- 11
- 16
Supongamos eso\( \mu(S) = \infty \) y\(A, \, B \in \mathscr S\) aquello con\(\mu(A \setminus B) = 2\),\(\mu(B \setminus A) = 3\), y\(\mu(A \cap B) = 4\). Encuentra la medida de cada uno de los siguientes conjuntos:
- \(A\)
- \(B\)
- \(A \cup B\)
- \( A^c \cap B^c \)
- \( A^c \cup B^c \)
Contestar
- 6
- 7
- 9
- \(\infty\)
- \(\infty\)
Supongamos eso\( \mu(S) = 10 \) y\(A, \, B \in \mathscr S\) aquello con\(\mu(A) = 3\),\(\mu(A \cup B) = 7\), y\(\mu(A \cap B) = 2\). Encuentra la medida de cada uno de los siguientes eventos:
- \(B\)
- \(A \setminus B\)
- \(B \setminus A\)
- \(A^c \cup B^c\)
- \(A^c \cap B^c\)
Contestar
- 6
- 1
- 4
- 8
- 3
Supongamos que\( A, \, B, \, C \in \mathscr S \) con\( \mu(A) = 10 \)\( \mu(B) = 12 \),\( \mu(C) = 15 \),\( \mu(A \cap B) = 3 \),\( \mu(A \cap C) = 4 \),,\( \mu(B \cap C) = 5 \), y\( \mu(A \cap B \cap C) = 1S \). Encuentra las probabilidades de los distintos sindicatos:
- \( A \cup B \)
- \( A \cup C \)
- \( B \cup C \)
- \( A \cup B \cup C \)
Contestar
- 21
- 23
- 22
- 28


