2.6: Convergencia
- Page ID
- 152198
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Esta es la primera de varias secciones de este capítulo que están más avanzadas que los temas básicos de las cinco primeras secciones. En esta sección se discuten varios temas relacionados con la convergencia de eventos y variables aleatorias, tema de fundamental importancia en la teoría de la probabilidad. En particular los resultados que obtengamos serán importantes para:
- Propiedades de las funciones de distribución,
- La débil ley de los grandes números,
- La fuerte ley de los grandes números.
Como es habitual, nuestro punto de partida es un experimento aleatorio modelado por un espacio de probabilidad\( (\Omega, \mathscr{F}, \P) \). Entonces, para revisar,\( \Omega \) es el conjunto de resultados,\( \mathscr F \) el\( \sigma \) álgebra de eventos, y\( \P \) la medida de probabilidad en el espacio muestral\( (\Omega, \mathscr F) \).
Teoría Básica
Secuencias de eventos
Nuestra primera discusión trata sobre secuencias de eventos y diversos tipos de límites de tales secuencias. Los límites también son eventos. Comenzamos con dos definiciones simples.
Supongamos que\( (A_1, A_2, \ldots) \) es una secuencia de eventos.
- La secuencia va en aumento si\( A_n \subseteq A_{n+1} \) por cada\( n \in \N_+ \).
- La secuencia es decreciente si\( A_{n+1} \subseteq A_n \) por cada\( n \in \N_+ \).
Tenga en cuenta que estas son las definiciones estándar de creciente y decreciente, relativa al orden total ordinario\( \le \) en el conjunto de índices\( \N_+ \) y el orden parcial del subconjunto\( \subseteq \) en la colección de eventos. La terminología también se justifica por las variables indicadoras correspondientes.
Supongamos que\( (A_1, A_2, \ldots) \) es una secuencia de eventos, y vamos a\(I_n = \bs 1_{A_n}\) denotar la variable indicadora del evento\(A_n\) para\(n \in \N_+\).
- La secuencia de eventos va en aumento si y sólo si la secuencia de variables indicadoras va en aumento en el sentido ordinario. Es decir,\(I_n \le I_{n+1}\) para cada uno\(n \in \N_+\).
- La secuencia de eventos es decreciente si y sólo si la secuencia de variables indicadoras disminuye en el sentido ordinario. Es decir,\(I_{n+1} \le I_n\) para cada uno\(n \in \ _+\).
Prueba
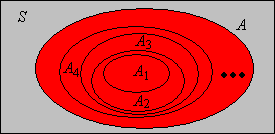
Figura\(\PageIndex{1}\): Una secuencia de eventos crecientes y su unión
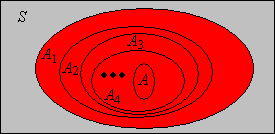
Figura\(\PageIndex{2}\): Una secuencia de eventos decrecientes y su intersección
Si una secuencia de eventos está aumentando o disminuyendo, podemos definir el límite de la secuencia de una manera que resulte bastante natural.
Supongamos que\( (A_1, A_2, \ldots) \) es una secuencia de eventos.
- Si la secuencia va en aumento, definimos\( \lim_{n \to \infty} A_n = \bigcup_{n=1}^\infty A_n \).
- Si la secuencia es decreciente, definimos\( \lim_{n \to \infty} A_n = \bigcap_{n=1}^\infty A_n \).
Una vez más, la terminología es aclarada por las variables indicadoras correspondientes.
Supongamos nuevamente que\( (A_1, A_2, \ldots) \) es una secuencia de eventos, y vamos a\(I_n = \bs 1_{A_n}\) denotar la variable indicadora de\(A_n\) for\(n \in \N_+\).
- Si la secuencia de eventos está aumentando, entonces\( \lim_{n \to \infty} I_n \) es la variable indicadora de\( \bigcup_{n = 1}^\infty A_n \)
- Si la secuencia de eventos es decreciente, entonces\( \lim_{n \to \infty} I_n \) es la variable indicadora de\( \bigcap_{n = 1}^\infty A_n \)
Prueba
- Si\( s \in \bigcup_{n=1}^\infty A_n\) entonces\( s \in A_k \) para algunos\( k \in \N_+ \). Ya que los eventos van en aumento,\( s \in A_n \) para cada uno\( n \ge k \). En este caso,\( I_n(s) = 1 \) para todos\( n \ge k \) y por lo tanto\( \lim_{n \to \infty} I_n(s) = 1 \). Por otro lado, si\( s \notin \bigcup_{n=1}^\infty A_n \) entonces\( s \notin A_n \) por cada\( n \in \N_+ \). En este caso,\( I_n(s) = 0\) para todos\( n \in \N_+ \) y por lo tanto\( \lim_{n \to \infty} I_n(s) = 0 \).
- Si\( s \in \bigcap_{n=1}^\infty A_n \) entonces\( s \in A_n \) para cada uno\( n \in \N_+ \). En este caso,\( I_n(s) = 1 \) para cada uno\( n \in \N_+ \) y por lo tanto\( \lim_{n \to \infty} I_n(s) = 1 \). Si\( s \notin \bigcap_{n=1}^\infty A_n\) entonces\( s \notin A_k \) para algunos\( k \in \N_+ \). Ya que los eventos van disminuyendo,\( s \notin A_n \) para todos\( n \ge k \). En este caso,\( I_n(s) = 0 \) para\( n \ge k \) y por lo tanto\( \lim_{n \to \infty} I_n(s) = 0 \).
Una unión arbitraria de eventos siempre se puede escribir como una unión de eventos crecientes, y una intersección arbitraria de eventos siempre se puede escribir como una intersección de eventos decrecientes:
Supongamos que\((A_1, A_2, \ldots)\) es una secuencia de eventos. Entonces
- \(\bigcup_{i = 1}^ n A_i\)está aumentando en\(n \in \N_+\) y\(\bigcup_{i = 1}^\infty A_i = \lim_{n \to \infty} \bigcup_{i = 1}^n A_i\).
- \(\bigcap_{i=1}^n A_i\)está disminuyendo en\(n \in \N_+\) y\(\bigcap_{i=1}^\infty A_i = \lim_{n \to \infty} \bigcap_{i=1}^n A_i\).
Prueba
- Trivialmente\( \bigcup_{i=1}^n A_i \subseteq \bigcup_{i=1}^{n+1} A_i \). El segundo enunciado simplemente significa eso\( \bigcup_{n=1}^\infty \bigcup_{i = 1}^n A_i = \bigcup_{i=1}^\infty A_i\).
- Trivialmente\( \bigcap_{i=1}^{n+1} A_i \subseteq \bigcap_{i=1}^n A_i \). El segundo enunciado simplemente significa eso\( \bigcap_{n=1}^\infty \bigcap_{i=1}^n A_i = \bigcap_{i=1}^\infty A_i \).
Existe una manera más interesante y útil de generar secuencias crecientes y decrecientes a partir de una secuencia arbitraria de eventos, utilizando el segmento de cola de la secuencia en lugar del segmento inicial.
Supongamos que\( (A_1, A_2, \ldots) \) es una secuencia de eventos. Entonces
- \(\bigcup_{i=n}^\infty A_i\)está disminuyendo en\(n \in \N_+\).
- \(\bigcap_{i=n}^\infty A_i\)está aumentando en\(n \in \N_+\).
Prueba
- Claramente\(\bigcup_{i=n+1}^\infty A_i \subseteq \bigcup_{i=n}^\infty A_i\)
- Claramente\(\bigcap_{i=n}^\infty A_i \subseteq \bigcap_{i=n+1}^\infty A_i\)
Dado que las nuevas secuencias definidas en los resultados anteriores son decrecientes y crecientes, respectivamente, podemos tomar sus límites. Estos son el límite superior y límite inferior, respectivamente, de la secuencia original.
Supongamos que\( (A_1, A_2, \ldots) \) es una secuencia de eventos. Definir
- \( \limsup_{n \to \infty} A_n = \lim_{n \to \infty} \bigcup_{i=n}^\infty A_i = \bigcap_{n=1}^\infty \bigcup_{i=n}^\infty A_i \). Este es el evento que ocurre si un solo si\( A_n \) ocurre por infinitamente muchos valores de\( n \).
- \( \liminf_{n \to \infty} A_n = \lim_{n \to \infty} \bigcap_{i=n}^\infty A_i = \bigcup_{n=1}^\infty \bigcap_{i=n}^\infty A_i \). Este es el evento que ocurre si un solo si\( A_n \) ocurre para todos pero finitamente muchos valores de\( n \).
Prueba
- A partir de la definición, el suceso\( \limsup_{n \to \infty} A_n \) ocurre si y sólo si para cada uno\( n \in \N_+ \) existe\( i \ge n \) tal que\( A_i \) se da.
- A partir de la definición, el suceso\( \liminf_{n \to \infty} A_n \) ocurre si y sólo si existe\( n \in \N_+ \) tal que\( A_i \) ocurre para cada uno\( i \ge n \).
Una vez más, la terminología y la notación son aclaradas por las variables indicadoras correspondientes. Es posible que deba revisar límite inferior y límite superior para secuencias de números reales en la sección de Órdenes Parciales.
Supongamos que\( (A_1, A_2, \ldots) \) es una secuencia de eventos, y et\(I_n = \bs 1_{A_n}\) denotan la variable indicadora de\(A_n\) for\(n \in \N_+\). Entonces
- \(\limsup_{n \to \infty} I_n \)es la variable indicadora de\(\limsup_{n \to \infty} A_n\).
- \(\liminf_{n \to \infty} I_n \)es la variable indicadora de\(\liminf_{n \to \infty} A_n\).
Prueba
- Por el resultado anterior,\( \lim_{n \to \infty} \bs 1\left(\bigcup_{i=n}^\infty A_i\right) \) es la variable indicadora de\( \limsup_{n \to \infty} A_n \). Pero\(\bs 1\left(\bigcup_{i=n}^\infty A_i\right) = \max\{I_i: i \ge n\}\) y por lo tanto\( \lim_{n \to \infty} \bs 1\left(\bigcup_{i=n}^\infty A_i\right) = \limsup_{n \to \infty} I_n \).
- Por el resultado anterior,\( \lim_{n \to \infty} \bs 1\left(\bigcap_{i=n}^\infty A_i\right) \) es la variable indicadora de\( \liminf_{n \to \infty} A_n \). Pero\(\bs 1\left(\bigcap_{i=n}^\infty A_i\right) = \min\{I_i: i \ge n\}\) y por lo tanto\( \lim_{n \to \infty} \bs 1\left(\bigcap_{i=n}^\infty A_i\right) = \liminf_{n \to \infty} I_n \).
Supongamos que\( (A_1, A_2, \ldots) \) es una secuencia de eventos. Entonces\(\liminf_{n \to \infty} A_n \subseteq \limsup_{n \to \infty} A_n\).
Prueba
Si\( A_n \) ocurre para todos pero finitamente muchos\( n \in \N_+ \) entonces ciertamente\( A_n \) ocurre para infinitamente muchos\( n \in \N_+ \).
Supongamos que\( (A_1, A_2, \ldots) \) es una secuencia de eventos. Entonces
- \(\left( \limsup_{n \to \infty} A_n \right)^c = \liminf_{n \to \infty} A_n^c\)
- \(\left( \liminf_{n \to \infty} A_n \right)^c = \limsup_{n \to \infty} A_n^c\).
Prueba
Estos resultados se derivan de las leyes de DeMorgan.
Los teoremas de la continuidad
En términos generales, una función es continua si conserva límites. Así, los siguientes resultados son los teoremas de continuidad de la probabilidad. La parte (a) es el teorema de continuidad para eventos crecientes y parte (b) el teorema de continuidad para eventos decrecientes.
Supongamos que\((A_1, A_2, \ldots)\) es una secuencia de eventos.
- Si la secuencia está aumentando entonces\(\lim_{n \to \infty} \P(A_n) = \P\left( \lim_{n \to \infty} A_n \right) = \P\left(\bigcup_{n=1}^\infty A_n\right)\)
- Si la secuencia es decreciente entonces\(\lim_{n \to \infty} \P(A_n) = \P\left( \lim_{n \to \infty} A_n \right) = \P\left(\bigcap_{n=1}^\infty A_n\right)\)
Prueba
- Dejar\(B_1 = A_1\) y dejar\(B_i = A_i \setminus A_{i-1}\) para\(i \in \{2, 3, \ldots\}\). Tenga en cuenta que la colección de eventos\(\{B_1, B_2, \ldots \}\) es disjunta por pares y tiene la misma unión que\(\{A_1, A_2, \ldots \}\). De la aditividad contable y la definición de series infinitas,\[ \P\left(\bigcup_{i=1}^\infty A_i\right) = \P\left(\bigcup_{i=1}^\infty B_i\right) = \sum_{i = 1}^\infty \P(B_i) = \lim_{n \to \infty} \sum_{i = 1}^n \P(B_i) \] Pero\( \P(B_1) = \P(A_1) \) y\( \P(B_i) = \P(A_i) - \P(A_{i-1}) \) para\( i \in \{2, 3, \ldots\} \). Por lo tanto\( \sum_{i=1}^n \P(B_i) = \P(A_n) \) y por lo tanto tenemos\( \P\left(\bigcup_{i=1}^\infty A_i\right) = \lim_{n \to \infty} \P(A_n) \).
La construcción en el teorema de continuidad para eventos crecientes 
- La secuencia de complementos\(\left(A_1^c, A_2^c, \ldots\right)\) va en aumento. De ahí usar la parte (a), la ley de DeMorgan, y la regla complementaria que tenemos\[ \P\left(\bigcap_{i=1}^\infty A_i \right) = 1 - \P\left(\bigcup_{i=1}^\infty A_i^c\right) = 1 - \lim_{n \to \infty} \P(A_n^c) = \lim_{n \to \infty} \left[1 - \P\left(A_n^c\right)\right] = \lim_{n \to \infty} \P(A_n) \]
Los teoremas de continuidad se pueden aplicar a las secuencias crecientes y decrecientes que construimos anteriormente a partir de una secuencia arbitraria de eventos.
Supongamos que\((A_1, A_2, \ldots)\) es una secuencia de eventos.
- \(\P\left( \bigcup_{i=1}^\infty A_i \right) = \lim_{n \to \infty} \P\left( \bigcup_{i = 1}^n A_i \right)\)
- \(\P\left( \bigcap_{i=1}^\infty A_i \right) = \lim_{n \to \infty} \P\left( \bigcap_{i = 1}^n A_i \right)\)
Prueba
Estos resultados se derivan inmediatamente de los teoremas de continuidad.
Supongamos que\( (A_1, A_2, \ldots) \) es una secuencia de eventos. Entonces
- \(\P\left(\limsup_{n \to \infty} A_n\right) = \lim_{n \to \infty} \P\left(\bigcup_{i=n}^\infty A_i\right)\)
- \(\P\left(\liminf_{n \to \infty} A_n\right) = \lim_{n \to \infty} \P\left(\bigcap_{i=n}^\infty A_i\right)\)
Prueba
Estos resultados se derivan directamente de las definiciones, y de los teoremas de continuidad.
El siguiente resultado muestra que el axioma de aditividad contable para una medida de probabilidad es equivalente a la aditividad finita y la propiedad de continuidad para eventos crecientes.
Temporalmente, supongamos que eso\( \P \) es solo finitamente aditivo, pero satisface la propiedad de continuidad para eventos crecientes. Entonces\( \P \) es contablemente aditivo.
Prueba
Supongamos que\( (A_1, A_2, \ldots) \) es una secuencia de eventos disjuntos por pares. Ya que estamos asumiendo que\( \P \) es finitamente aditivo tenemos\[ \P\left(\bigcup_{i=1}^n A_i\right) = \sum_{i=1}^n \P(A_i) \] Si dejamos\( n \to \infty \), el lado izquierdo converge a\( \P\left(\bigcup_{i=1}^\infty A_i\right) \) por la suposición de continuidad y el resultado anterior, mientras que el lado derecho converge a\( \sum_{i=1}^\infty \P(A_i) \) por la definición de una serie infinita.
Hay algunos matemáticos que rechazan el axioma de aditividad contable de medida de probabilidad a favor del axioma de aditividad finita más débil. Cualesquiera que sean los argumentos filosóficos, la vida es ciertamente mucho más difícil sin los teoremas de continuidad.
Los Lemmas de Borel-Cantelli
Los Lemmas de Borel-Cantelli, que llevan el nombre de Emil Borel y Francessco Cantelli, son herramientas muy importantes en la teoría de la probabilidad. El primer lema da una condición que es suficiente para concluir que infinitamente muchos eventos ocurren con probabilidad 0.
Primero Lema de Borel-Cantelli. Supongamos que\( (A_1, A_2, \ldots) \) es una secuencia de eventos. Si\(\sum_{n=1}^\infty \P(A_n) \lt \infty\) entonces\(\P\left(\limsup_{n \to \infty} A_n\right) = 0\).
Prueba
Del resultado anterior sobre superiores límite, tenemos\( \P\left(\limsup_{n \to \infty} A_n\right) = \lim_{n \to \infty} \P\left(\bigcup_{i = n}^\infty A_i \right) \). Pero a partir de la desigualdad de Boole,\( \P\left(\bigcup_{i = n}^\infty A_i \right) \le \sum_{i = n}^\infty \P(A_i) \). Ya que\( \sum_{i = 1}^\infty \P(A_i) \lt \infty \), tenemos\( \sum_{i = n}^\infty \P(A_i) \to 0 \) como\( n \to \infty \).
El segundo lema da una condición que es suficiente para concluir que infinitamente muchos eventos independientes ocurren con probabilidad 1.
Segundo Lema de Borel-Cantelli. Supongamos que\((A_1, A_2, \ldots)\) es una secuencia de eventos independientes. Si\(\sum_{n=1}^\infty \P(A_n) = \infty\) entonces\(\P\left( \limsup_{n \to \infty} A_n \right) = 1\).
Prueba
Tenga en cuenta primero que\(1 - x \le e^{-x}\) para cada\(x \in \R\), y hcnce\( 1 - \P(A_i) \le \exp\left[-\P(A_i)\right] \) para cada uno\( i \in \N_+ \). De los resultados anteriores sobre límites superiores y complementos,\[ \P\left[\left(\limsup_{n \to \infty} A_n\right)^c\right] = \P\left(\liminf_{n \to \infty} A_n^c\right) = \lim_{n \to \infty} \P \left(\bigcap_{i = n}^\infty A_i^c\right) \] Pero por la independencia y la desigualdad anterior,\[ \P\left(\bigcap_{i = n}^\infty A_i^c\right) = \prod_{i = n}^\infty \P\left(A_i^c\right) = \prod_{i = n}^\infty \left[1 - \P(A_i)\right] \le \prod_{i = n}^\infty \exp\left[-\P(A_i)\right] = \exp\left(-\sum_{i = n}^\infty \P(A_i) \right) = 0 \]
Para eventos independientes, ambos lemmas de Borel-Cantelli se aplican por supuesto, y conducen a una ley de cero uno.
Si\( (A_1, A_2, \ldots) \) es una secuencia de eventos independientes entonces\( \limsup_{n \to \infty} A_n \) tiene probabilidad 0 o 1:
- Si\(\sum_{n=1}^\infty \P(A_n) \lt \infty\) entonces\(\P\left( \limsup_{n \to \infty} A_n \right) = 0\).
- Si\(\sum_{n=1}^\infty \P(A_n) = \infty\) entonces\(\P\left( \limsup_{n \to \infty} A_n \right) = 1\).
Este resultado es en realidad un caso especial de una ley más general de cero uno, conocida como la ley Kolmogorov cero-uno, y llamada así por Andrei Kolmogorov. Esta ley se estudia en la sección más avanzada sobre la medida. También, podemos usar la ley cero-uno para derivar un teorema de cálculo que relaciona series infinitas y productos infintos. Esta derivación es un ejemplo del método probabilístico —el uso de la probabilidad para obtener resultados, aparentemente no relacionados con la probabilidad, en otras áreas de las matemáticas.
Supongamos que\( p_i \in (0, 1) \) para cada uno\( i \in \N_+ \). Entonces\[ \prod_{i=1}^\infty p_i \gt 0 \text{ if and only if } \sum_{i=1}^\infty (1 - p_i) \lt \infty \]
Prueba
Podemos construir fácilmente un espacio de probabilidad con una secuencia de eventos independientes\( (A_1, A_2, \ldots) \) tal que\( \P(A_i) = 1 - p_i \) para cada uno\( i \in \N_+ \). El resultado se desprende entonces de las pruebas de los dos lemmas de Borel-Cantelli.
Nuestro siguiente resultado es una simple aplicación del segundo lema de Borel-Cantelli a replicaciones independientes de un experimento básico.
Supongamos que\(A\) es un evento en un experimento aleatorio básico con\(\P(A) \gt 0\). En el experimento compuesto que consiste en replicaciones independientes del experimento básico, el evento \(A\)ocurre infinitamente a menudo
tiene probabilidad 1.
Prueba
Dejar\( p \) denotar la probabilidad de\( A \) en el experimento básico. En el experimento compuesto, tenemos una secuencia de eventos independientes\( (A_1, A_2, \ldots) \) con\( \P(A_n) = p \) para cada uno\( n \in \N_+ \) (estos son copias independientes
de\( A \)). Pero\( \sum_{n=1}^\infty \P(A_n) = \infty \) como\( p \gt 0 \) así se desprende el resultado del segundo lema de Borel-Cantelli.
Convergencia de variables aleatorias
Nuestra siguiente discusión se refiere a dos formas en que una secuencia de variables aleatorias definidas para nuestro experimento puede converger
. Estos son conceptos fundamentalmente importantes, ya que algunos de los resultados más profundos en la teoría de la probabilidad son teoremas de límite que involucran variables aleatorias. El caso especial más importante es cuando las variables aleatorias son de valor real, pero las pruebas son esencialmente las mismas para las variables con valores en un espacio métrico, por lo que usaremos la configuración más general.
Así, supongamos que\( (S, d) \) es un espacio métrico, y ese\(\mathscr S \) es el\( \sigma \) álgebra de Borel correspondiente (es decir, la\( \sigma \) -álgebra generada por la topología), de manera que nuestro espacio medible es\( (S, \mathscr S) \). Aquí está el caso especial más importante:
Porque\( n \in \N_+ \), es el espacio\( n \) -dimensional Euclideano es\( (\R^n, d_n) \) donde\[ d_n(\bs x, \bs y) = \sqrt{\sum_{i=1}^n (y_i - x_i)^2}, \quad \bs x = (x_1, x_2 \ldots, x_n), \, \bs y = (y_1, y_2, \ldots, y_n) \in \R^n \]
Los espacios euclidianos llevan el nombre de Euclides, por supuesto. Como se señaló anteriormente, el caso unidimensional donde\( d(x, y) = |y - x| \) for\( x, \, y \in \R \) es particularmente importante. Volviendo al espacio métrico general, recordemos que si\( (x_1, x_2, \ldots) \) es una secuencia en\( S \) y\( x \in S \), entonces\( x_n \to x\) como\( n \to \infty \) significa eso\( d(x_n, x) \to 0 \) como\( n \to \infty \) (en el sentido habitual del cálculo). Para el resto de nuestra discusión, asumimos que\( (X_1, X_2, \ldots) \) es una secuencia de variable aleatoria con valores en\( S \) y\( X \) es una variable aleatoria con valores en\( S \), todos definidos en el espacio de probabilidad\( (\Omega, \mathscr F, \P) \).
Decimos que\(X_n \to X\) como\(n \to \infty\) con probabilidad 1 si el evento que\( X_n \to X \) como\( n \to \infty \) tiene probabilidad 1. Es decir,\[\P\{\omega \in S: X_n(\omega) \to X(\omega) \text{ as } n \to \infty\} = 1\]
Detalles
Tenemos que asegurarnos de que la definición tenga sentido, en que la afirmación que\( X_n \) converge a\( X \) como\( n \to \infty \) define un evento válido. Tenga en cuenta que\(X_n\) no converge\(X\) como\(n \to \infty\) si y sólo si para algunos\(\epsilon \gt 0\),\(d(X_n, X) \gt \epsilon\) para infinitamente muchos\(n \in \N_+\). Tenga en cuenta que si esta condición se mantiene para un dado\( \epsilon \gt 0 \), entonces se mantiene para todos los más pequeños\( \epsilon \gt 0 \). Además, hay arbitrariamente pequeños racionales\( \epsilon \gt 0 \) por lo que\(X_n\) no converge\(X\) como\(n \to \infty\) si y sólo si para algunos racionales\(\epsilon \gt 0\),\(d(X_n, X) \gt \epsilon\) para infinitamente muchos\(n \in \N_+\). De ahí\[ \left\{X_n \to X \text{ as } n \to \infty\right\}^c = \bigcup_{\epsilon \in \Q_+} \limsup_{n \to \infty} \left\{d(X_n, X) \gt \epsilon\right\} \] donde\( \Q_+ \) está el conjunto de números racionales positivos. Un punto crítico a recordar es que este conjunto es contable. Entonces, construyendo un poco a la vez, tenga en cuenta que\( \left\{d(X_n, X) \gt \epsilon\right\} \) es un evento para cada uno\( \epsilon \in \Q_+ \) y\( n \in \N_+ \) desde\( X_n \) y\( X \) son variables aleatorias. A continuación, el límite superior de una secuencia de eventos es un evento. Por último, una unión contable de eventos es un evento.
Como buenos probabilistas, solemos suprimir las referencias al espacio muestral y escribir la definición simplemente como\( \P(X_n \to X \text{ as } n \to \infty) = 1 \). La afirmación de que un evento tiene probabilidad 1 suele ser la afirmación afirmativa más fuerte que podemos hacer en la teoría de la probabilidad. Así, la convergencia con probabilidad 1 es la forma más fuerte de convergencia. A veces se usan las frases con casi seguridad y casi en todas partes en lugar de la frase con probabilidad 1.
Recordemos que las métricas\( d \) y\( e \) on\( S \) son equivalentes si generan la misma topología en\( S \). Recordemos también que la convergencia de una secuencia es una propiedad topológica. Es decir, si\( (x_1, x_2, \ldots) \) es una secuencia en\( S \) y\( x \in S \), y si\( d, \, e \) son métricas equivalentes en\( S \), entonces\( x_n \to x \) como\( n \to \infty \) relativo a\( d \) if y solo si\( x_n \to x \) como\( n \to \infty \) relativo a\( e \). Entonces para nuestras variables aleatorias como se definió anteriormente, se deduce que\( X_n \to X \) como\( n \to \infty \) con probabilidad 1 relativo a\( d \) si y solo si\( X_n \to X \) como\( n \to \infty \) con probabilidad 1 relativo a\( e \).
Las siguientes declaraciones son equivalentes:
- \( X_n \to X \)como\( n \to \infty \) con probabilidad 1.
- \(\P\left[d(X_n, X) \gt \epsilon \text{ for infinitely many } n \in \N_+\right] = 0 \)para cada racional\(\epsilon \gt 0\).
- \(\P\left[d(X_n, X) \gt \epsilon \text{ for infinitely many } n \in \N_+\right] = 0\)para cada\(\epsilon \gt 0\).
- \(\P\left[d(X_k, X) \gt \epsilon \text{ for some } k \ge n\right] \to 0\)como\(n \to \infty\) para cada\(\epsilon \gt 0\).
Prueba
De los detalles en la definición anterior,\( \P(X_n \to X \text{ as } n \to \infty) = 1 \) si y sólo si\[ \P\left(\bigcup_{\epsilon \in \Q_+} \left\{d(X_n, X) \gt \epsilon \text{ for infinitely many } n \in \N_+\right\} \right) = 0 \] donde de nuevo\( \Q_+ \) es el conjunto de números racionales positivos. Pero por la desigualdad de Boole, una unión contable de eventos tiene probabilidad 0 si y solo si cada evento en la unión tiene probabilidad 0. Por lo tanto, (a) equivale a (b). El enunciado b) es claramente equivalente a (c) ya que existen arbitrariamente pequeños números racionales positivos. Finalmente, (c) es equivalente a (d) por el resultado de continuidad anterior.
Nuestro siguiente resultado da un criterio fundamental para la convergencia con probabilidad 1:
Si\(\sum_{n=1}^\infty \P\left[d(X_n, X) \gt \epsilon\right] \lt \infty\) por cada\(\epsilon \gt 0\) entonces\(X_n \to X\) como\(n \to \infty\) con probabilidad 1.
Prueba
Por el primer lema de Borel-Cantelli, si\(\sum_{n=1}^\infty \P\left[d(X_n, X) \gt \epsilon\right) \lt \infty\) entonces\(\P\left[d(X_n, X) \gt \epsilon \text{ for infinitely many } n \in \N_+\right) = 0\). De ahí que el resultado se deduce del teorema anterior.
Aquí está nuestro siguiente modo de convergencia.
Decimos que\(X_n \to X\) como\(n \to \infty\) en probabilidad si\[\P\left[d(X_n, X) \gt \epsilon\right] \to 0 \text{ as } n \to \infty \text{ for each } \epsilon \gt 0\]
La frase en probabilidad suena superficialmente como la frase con probabilidad 1. No obstante, como veremos pronto, la convergencia en probabilidad es mucho más débil que la convergencia con probabilidad 1. De hecho, la convergencia con probabilidad 1 a menudo se denomina convergencia fuerte, mientras que la convergencia en probabilidad a menudo se denomina convergencia débil.
Si\(X_n \to X\) como\(n \to \infty\) con probabilidad 1 entonces\(X_n \to X\) como\(n \to \infty\) en probabilidad.
Prueba
Vamos\( \epsilon \gt 0 \). Entonces\( \P\left[d(X_n, X) \gt \epsilon\right] \le \P\left[d(X_k, X) \gt \epsilon \text{ for some } k \ge n\right]\). Pero si\( X_n \to X \) como\( n \to \infty \) con probabilidad 1, entonces la expresión de la derecha converge a 0 como\( n \to \infty \) por la parte (d) del resultado anterior. De ahí\( X_n \to X \) como\( n \to \infty \) en probabilidad.
Lo contrario falla con pasión. A continuación se da un simple contraejemplo. Sin embargo, hay una conversación parcial que es muy útil.
Si\(X_n \to X\) como\(n \to \infty\) en probabilidad, entonces existe una subsecuencia\((n_1, n_2, n_3 \ldots)\) de\(\N_+\) tal que\(X_{n_k} \to X\) como\(k \to \infty\) con probabilidad 1.
Prueba
Supongamos que\( X_n \to X \) como\( n \to \infty \) en probabilidad. Entonces para cada uno\(k \in \N_+\) existe\(n_k \in \N_+\) tal que\(\P\left[d\left(X_{n_k}, X \right) \gt 1 / k \right] \lt 1 / k^2\). Podemos tomar las decisiones\(n_k \lt n_{k+1}\) para que para cada uno\(k\). De ello se deduce que\(\sum_{k=1}^\infty \P\left[d\left(X_{n_k}, X\right) \gt \epsilon \right] \lt \infty\) para cada\(\epsilon \gt 0\). Por el resultado anterior,\(X_{n_k} \to X\) como\(n \to \infty\) con probabilidad 1.
Tenga en cuenta que la prueba funciona porque\(1 / k \to 0\) como\(k \to \infty\) y\(\sum_{k=1}^\infty 1 / k^2 \lt \infty\). Dos secuencias cualesquiera con estas propiedades funcionarían igual de bien.
Hay otros dos modos de convergencia que discutiremos más adelante:
- Convergencia en la distribución.
- Convergencia en media,
Ejemplos y Aplicaciones
Monedas
Supongamos que tenemos una secuencia infinita de monedas etiquetadas\(1, 2, \ldots\) Además, la moneda\(n\) tiene probabilidad de cabezas\(1 / n^a\) para cada una\(n \in \N_+\), donde\(a \gt 0\) es un parámetro. Una vez tiramos cada moneda en secuencia. En términos de\(a\), encontrar la probabilidad de los siguientes eventos:
- infinitamente muchas cabezas ocurren
- infinitamente muchas colas ocurren
Contestar
\(H_n\)Sea el evento que arroje\(n\) los resultados en cabezas, y\(T_n\) el evento que arroje\(n\) resulte en colas.
- \(\P\left(\limsup_{n \to \infty} H_n\right) = 1\),\(\P\left(\limsup_{n \to \infty} T_n\right) = 1\) si\(a \in (0, 1]\)
- \(\P\left(\limsup_{n \to \infty} H_n\right) = 0\),\(\P\left(\limsup_{n \to \infty} T_n\right) = 1\) si\(a \in (1, \infty)\)
El siguiente ejercicio da un ejemplo sencillo de una secuencia de variables aleatorias que convergen en probabilidad pero no con probabilidad 1. Naturalmente, estamos asumiendo la métrica estándar en\( \R \).
Supongamos nuevamente que tenemos una secuencia de monedas etiquetadas\(1, 2, \ldots\), y esa moneda\(n\) aterriza boca arriba con probabilidad\(\frac{1}{n}\) para cada una\(n\). Lanzamos las monedas para producir una secuencia\((X_1, X_2, \ldots)\) de variables aleatorias indicadoras independientes con\[\P(X_n = 1) = \frac{1}{n}, \; \P(X_n = 0) = 1 - \frac{1}{n}; \quad n \in \N_+\]
- \(\P(X_n = 0 \text{ for infinitely many } n) = 1\), de manera que infinitamente muchas colas ocurren con probabilidad 1.
- \(\P(X_n = 1 \text{ for infinitely many } n) = 1\), de manera que infinitamente muchas cabezas ocurren con probabilidad 1.
- \(\P(X_n \text{ does not converge as } n \to \infty) = 1\).
- \(X_n \to 0\)como\(n \to \infty\) en probabilidad.
Prueba
- Esto se desprende del segundo lema de Borel-Cantelli, ya que\( \sum_{n = 1}^\infty \P(X_n = 0) = \infty \)
- Esto también se desprende del segundo lema de Borel-Cantelli, ya que\( \sum_{n = 1}^\infty \P(X_n = 1) = \infty \).
- Esto se desprende de las partes a) y b). Recordemos que la intersección de dos eventos con probabilidad 1 todavía tiene probabilidad 1.
- Supongamos\( 0 \lt \epsilon \lt 1 \). Entonces\( \P\left(\left|X_n - 0\right| \gt \epsilon\right) = \P(X_n = 1) = \frac{1}{n} \to 0 \) como\( n \to \infty \).
Espacios Discretos
Recordemos que un espacio medible\( (S, \mathscr S) \) es discreto si\( S \) es contable y\( \mathscr S \) es la colección de todos los subconjuntos de\( S \) (el conjunto de potencia de\( S \)). Además,\( \mathscr S \) es el\( \sigma \) álgebra de Borel correspondiente a la métrica\( d \) discreta\( S \) dada por\( d(x, x) = 0 \) para\( x \in S \) y\( d(x, y) = 1 \) para distinto\( x, \, y \in S \). ¿Cómo funcionan la convergencia con probabilidad 1 y la convergencia en probabilidad para la métrica discreta?
Supongamos que\( (S, \mathscr S) \) es un espacio discreto. Supongamos además que\( (X_1, X_2, \ldots) \) es una secuencia de variables aleatorias con valores en\( S \) y\( X \) es una variable aleatoria con valores en\( S \), todos definidos en el espacio de probabilidad\( (\Omega, \mathscr F, \P) \). En relación con la métrica discreta\( d \),
- \( X_n \to X \)como\( n \to \infty \) con probabilidad 1 si y sólo si\( \P(X_n = X \text{ for all but finitely many } n \in \N_+) = 1 \).
- \( X_n \to X \)como\( n \to \infty \) en probabilidad si y sólo si\( \P(X_n \ne X) \to 0 \) como\( n \to \infty \).
Prueba
- Si\( (x_1, x_2, \ldots) \) es una secuencia de puntos en\( S \) y\( x \in S \), entonces relativo a métrica\( d \),\( x_n \to x \) como\( n \to \infty \) si y sólo si\( x_n = x \) para todos pero finitamente muchos\( n \in \N_+ \).
- Si\( \epsilon \ge 1 \) entonces\( \P[d(X_n, X) \gt \epsilon] = 0 \). Si\( \epsilon \in (0, 1) \) entonces\( \P[d(X_n, X) \gt \epsilon] = \P(X_n \ne X) \).
Por supuesto, es importante darse cuenta de que un espacio discreto puede ser el espacio Borel para métricas distintas a la métrica discreta.


