1.2: Integración numérica

Hay muchas ocasiones en las que uno puede desear integrar una expresión numéricamente en lugar de analíticamente. A veces no se puede encontrar una expresión analítica para una integral, o, si se puede, es tan complicada que es tan rápida de integrar numéricamente como lo es tabular la expresión analítica. O uno puede tener una tabla de números para integrar en lugar de una ecuación analítica. Muchas computadoras y calculadoras programables tienen rutinas internas para la integración, a las que se puede recurrir (en riesgo) sin tener idea de cómo funcionan. Se supone que el lector de este capítulo, sin embargo, quiere poder llevar a cabo una integración numérica sin recurrir a una rutina existente que haya sido escrita por otra persona.

Existen muchos métodos diferentes de integración numérica, pero el conocido como Regla de Simpson es fácil de programar, rápido de realizar y generalmente muy preciso. (Thomas Simpson, 1710 - 1761, fue un matemático inglés, autor de Un nuevo tratado sobre los fluxiones.)

Supongamos\(y(x)\) que tenemos una función que deseamos integrar entre dos límites. Calculamos el valor de la función en los dos límites y a medio camino entre ellos, por lo que ahora conocemos tres puntos en la curva. Luego encajamos una parábola a estos tres puntos y encontramos el área debajo de eso.

En la figura\(\text{I.1}\),\(y(x)\) está la función que deseamos integrar entre los límites\(x_2 − δx\) y\(x_2 + δx\). Es decir, deseamos calcular el área bajo la curva. \(y_1\),\(y_2\) y\(y_3\) son los valores de

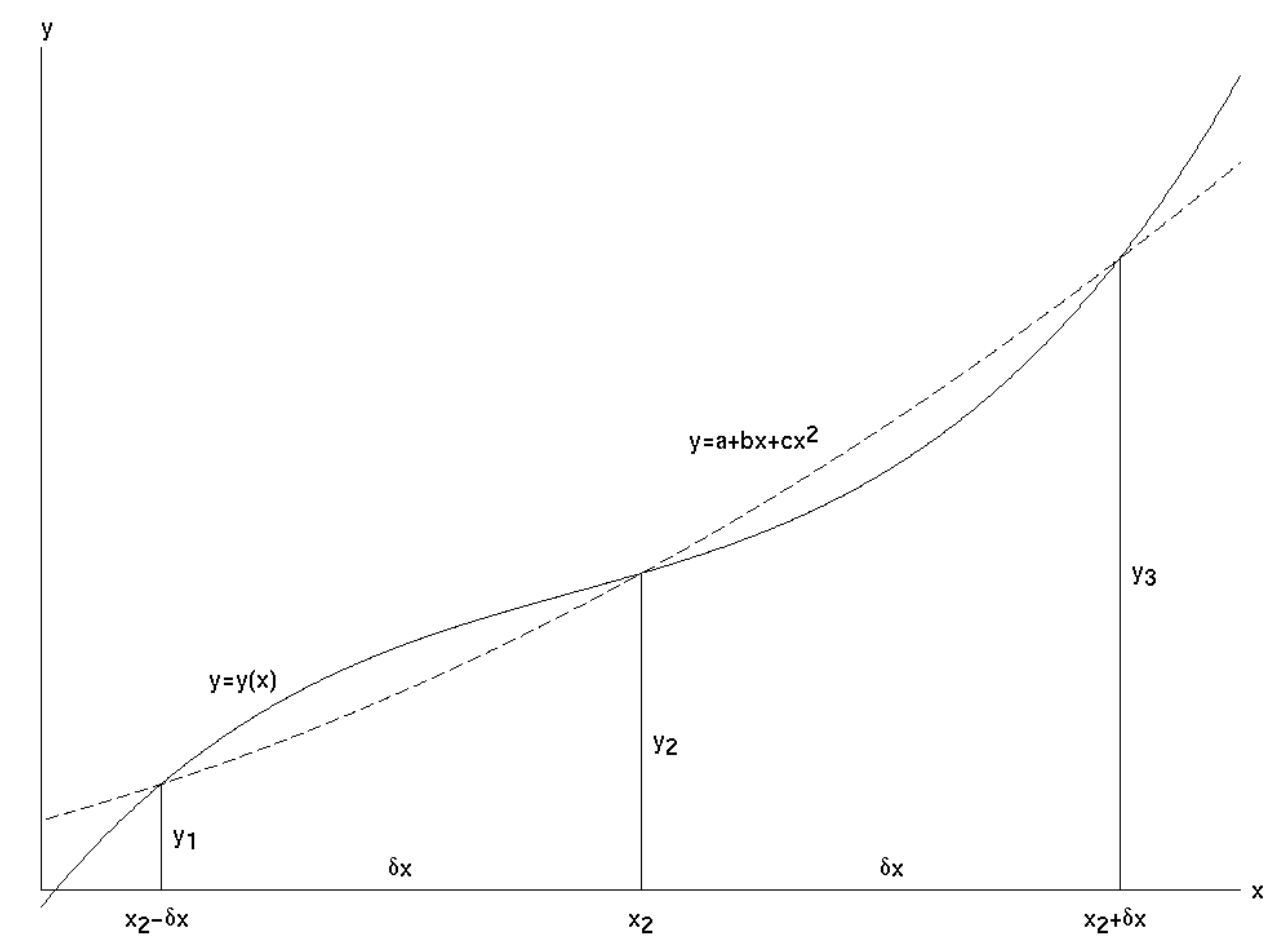
\(\text{FIGURE I.1}\)La Regla de Simpson nos da el área bajo la parábola (curva discontinua) que pasa por tres puntos en la curva\(y =y(x)\). Esto es aproximadamente igual al área debajo\(y = y(x)\).

la función en\(x_2 - δ_x, \ x_2\) y\(x_2 + δ_x\), y\(y = a + bx + cx^2\) es la parábola que pasa por los puntos\((x_2 - δx, y_1)\),\((x_2, y_2)\) y\((x_2 + δx, y_3)\).

Si la parábola va a pasar por estos tres puntos, debemos tener

\[y_1 = a + b(x_2 - δx) + c(x_2 - δx)^2 \label{1.2.1}\]

\[y_2 = a + bx + cx^2 \label{1.2.2}\]

\[y_3 = a + b(x_2 + δx) + c(x_2 + δx)^2 \label{1.2.3}\]

Podemos resolver estas Ecuaciones para encontrar los valores de\(a\),\(b\) y\(c\). Estos son

\[a=y_2 - \frac{x_2(y_3-y_1)}{2δx} + \frac{x_2^2 (y_3 - 2y_2 + y_1)}{2(δx)^2} \label{1.2.4}\]

\[b = \frac{y_3 - y_1}{2δx} - \frac{x_2 (y_3 - 2y_2 + y_1)}{(δx)^2} \label{1.2.5}\]

\[c = \frac{y_3 - 2y_2 + y_1}{2(δx)^2} \label{1.2.6}\]

Ahora el área debajo de la parábola (que se toma para ser aproximadamente el área debajo\(y(x)\)) es

\[\int_{x_2-δx}^{x_2+δx} \left( a+bx + cx^2 \right) dx = 2 \left[ a+bx_2 + cx_2^2 + \frac{1}{3} c (δx)^2 \right] δx \label{1.2.7}\]

Al sustituir los valores de\(a\),\(b\) y\(c\), obtenemos para el área bajo la parábola

\[\frac{1}{3} (y_1 + 4y_2 + y_3 ) δx \label{1.2.8}\]

y esta es la fórmula conocida como la Regla de Simpson.

Por un ejemplo, evaluemos\(\int_0^{\pi/2} \sin xdx\).

Evaluaremos la función en los límites inferior y superior y a medio camino entre ellos. Así

\ begin {array} {l l}
x= 0, & y=0\\
x =\ pi/4, & y=1/\ sqrt {2}\\
x =\ pi/2, & y=1\\
\ nonumber
\ end {array}

El intervalo entre valores consecutivos de\(x\) es\(δx = \pi/4\).

De ahí que la Regla de Simpson dé para el área

\[\frac{1}{3} \left( 0 + \frac{4}{\sqrt{2}}+ 1 \right) \frac{\pi}{4}\nonumber \]

que, a tres cifras significativas, lo es\(1.00\). Las gráficas de\(\sin x\) y\(a + bx + cx^2\) se muestran en la figura\(\text{I.2a}\). Los valores de\(a\),\(b\) y\(c\), obtenidos de las fórmulas anteriores, son

\[a=0, \quad b = \frac{\sqrt{32}-2}{\pi}, \quad c = \frac{8-\sqrt{128}}{\pi^2} \nonumber\]

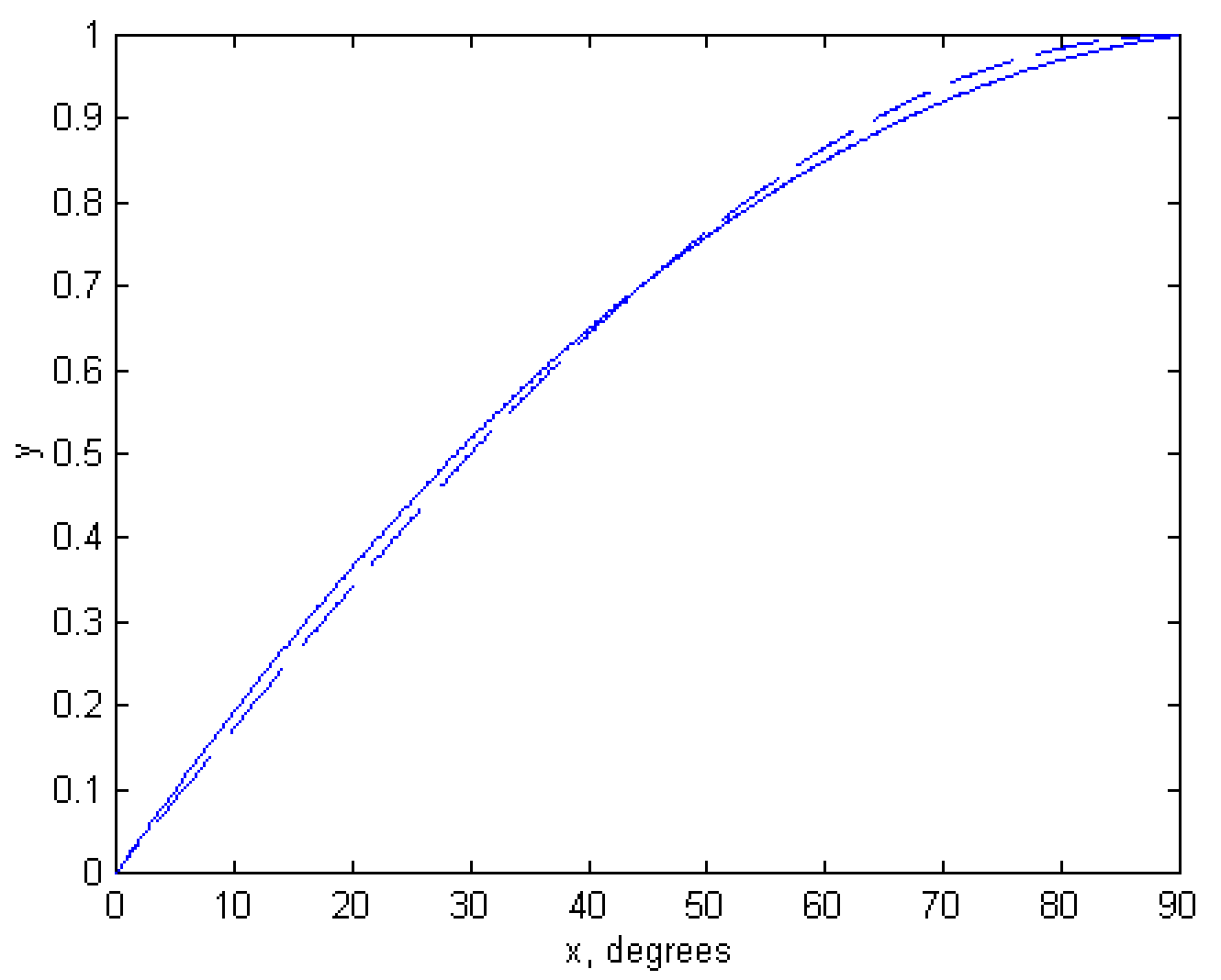
\(\text{FIGURE I.2a}\)

El resultado que acabamos de obtener es bastante espectacular, y no siempre somos tan afortunados. No todas las funciones pueden aproximarse tan bien por una parábola. Pero claro que el intervalo\(δx = \pi/4\) era ridículamente grosero. En la práctica subdividimos el intervalo en numerosos intervalos muy pequeños. Por ejemplo, considere la integral

\[\int_0^{\pi/4} \cos^{\frac{3}{2}} 2x \sin x\,dx .\nonumber\]

Subdividamos el intervalo\(0\)\(\pi/4\) en diez intervalos de ancho\(\pi /40\) cada uno. Evaluaremos la función en los puntos finales y los nueve puntos intermedios, así:

\ begin {array} {c c}
x &\ cos^ {\ frac {3} {2}} x\ sin xdx\\
0 & y_1 = 0.000\ 000\ 000\
\ pi/40 & y_2 = 0.077\ 014\ 622\
2\ pi/40 & y_3 = 0.145\ 091\ 486\
3\ pi/40 & y_4 = 0.196\ 339\ 002\\
4\ pi/ 40 & y_5 = 0.224\ 863\ 430\\
5\ pi/40 & y_6 = 0.227\ 544\ 930\
6\ pi/40 & y_7 = 0.204\ 585\ 473\
7\ pi/40 & y_8 = 0.159\ 828\ 877\
8\ pi/40 & y_9 = 0.100\ 969\ 971\\
9\ pi/40 & y_ {10} = 0.040\ 183 \ 066\\
10\ pi/40 & y_ {11} = 0.000\ 000\ 000\
\ nonumber
\ end {array}

La integral de\(0\) a\(2\pi /40\) es\(\frac{1}{3} (y_1 + 4y_2 + y_3) δx, \ δx\) ser el intervalo\(\pi/40\). La integral de\(3\pi/40\) a\(4\pi/40\) es\(\frac{1}{3} ( y_3 +4y_4 +y_5 ) δx\). Y así sucesivamente, hasta llegar a la integral de\(8\pi/40\) a\(10\pi/40\). Cuando sumamos todos estos, obtenemos para la integral de\(0\) a\(\pi /4\),

\[\frac{1}{3} \left( y_1 + 4y_2 + 2y_3 + 4y_4 + 2y_5 + ... ... + 4y_{10} + y_{11} \right) δx \nonumber\]

\[=\frac{1}{3} [ y_1 + y_{11} + (y_2 + y_4 + y_6 + y_8 + y_{10} ) + 2(y_3 + y_5 + y_7 + y_9 ) ] δx, \nonumber\]

que viene a\(0.108 \ 768 \ 816\).

Vemos que el cálculo es bastante rápido, y es fácilmente programable (¡pruébalo!). Pero, ¿qué tan buena es la respuesta? ¿Es bueno tres cifras significativas? ¿Cuatro? ¿Cinco?

Dado que es bastante fácil programar el procedimiento para una computadora, mi práctica es subdividir el intervalo sucesivamente en\(10\),\(100\),\(1000\) subintervalos, y ver si el resultado converge. En el presente ejemplo, con\(N\) subintervalos, encontré los siguientes resultados:

\ begin {array} {r c}
N &\ text {integral}\
\\\
10 & 0.108\ 768\ 816\
100 & 0.108\ 709\ 621\
1000 & 0.108\ 709\ 466\
10000 & 0.108\ 709\ 465\
\ nonumber
\ end { matriz}

Esto demuestra que, incluso con una división del curso en diez intervalos, se obtiene un resultado bastante bueno, pero sí hay que trabajar para cifras más significativas. Estaba usando una computadora central cuando hice el cálculo con\(10000\) intervalos, y la respuesta se mostraba en mi pantalla en lo que estimaría era aproximadamente una quinta parte de segundo.

Hay dos lecciones más que aprender de este ejemplo. Una es que a veces un cambio de variable hará las cosas mucho más rápidas. Por ejemplo, si uno hace uno de los (¿bastante obvio?) sustituciones de prueba\(y = \cos x\),\(y = \cos 2x\) o\(y^2 = \cos 2x\), la integral se convierte

\[ \int_{1/\sqrt{2}}^1 (2y^2 - 1 )^{3/2} dy, \quad \int_0^1 \sqrt{\frac{y^3}{8(1+y)}} dy \quad \text{or} \quad \int_0^1 \frac{y^4}{\sqrt{2(1+y^2)}}dy. \nonumber\]

No sólo es mucho más rápido calcular cualquiera de estos integrands que la expresión trigonométrica original, sino que encontré la respuesta\(0.108 \ 709 \ 465\) por regla de Simpson en el tercero de estos con solo\(100\) intervalos en lugar de\(10,000\), la respuesta que aparece en la pantalla aparentemente instantáneamente. (Los dos primeros requirieron algunos intervalos más.)

Ganar alrededor de una quinta parte de segundo puede parecer de pequeño momento, pero en verdad el cálculo fue más rápido por un factor de varios cientos. A veces se escuchan cálculos muy grandes que involucran cantidades masivas de datos que requieren ejecuciones de computadora durante la noche de ocho horas más o menos. Si la velocidad y eficiencia de programación pudiera incrementarse en un factor de unos pocos cientos, como en este ejemplo, el cómputo completo podría completarse en menos de un minuto.

La otra lección que hay que aprender es que la integral sí, después de todo, tiene una forma algebraica explícita. Deberías tratar de encontrarlo, no solo para la práctica de integración, sino para convencerte de que de hecho hay ocasiones en las que una solución numérica se puede encontrar más rápido que una analítica. La respuesta, por cierto, es\(\frac{\sqrt{18}\ln(1+\sqrt{2}) - 2}{16}.\)

Ahora puede que desee realizar la siguiente integración numéricamente, ya sea por calculadora manual o por computadora.

\[\int_0^2 \frac{x^2 dx}{\sqrt{2-x}} \nonumber\]

A primera vista, esto puede parecer solo otro ejercicio de rutina, pero muy pronto encontrarás una pequeña dificultad y te preguntarás qué hacer al respecto. La dificultad es que, en el límite superior de la integración, el integrando se vuelve infinito. Este tipo de dificultad, que no es infrecuente, a menudo se puede superar por medio de un cambio de variable. Por ejemplo, let\(x = 2 \sin^2 \theta\), y la integral se convierte

\[ 8 \sqrt{2} \int_0^{\pi/2} \sin^5 \theta d \theta \nonumber\]

y la dificultad se ha ido. El lector debe tratar de integrar esto numéricamente por la regla de Simpson, aunque también puede señalarse que tiene una respuesta analítica exacta, a saber\(\sqrt{8192}/15\).

Aquí hay otro ejemplo. Se puede demostrar que el período de oscilación de un simple péndulo de longitud que se\(l\) balancea a ambos\(90^\circ\) lados de la vertical es

\[P = \sqrt{\frac{8l}{g}} \int_0^{\pi/2} \sqrt{\sec \theta} d\theta . \nonumber\]

Como en el ejemplo anterior, el integrando se vuelve infinito en el límite superior. Dejo al lector encontrar un cambio adecuado de variable tal que el integrando sea finito en ambos límites, y luego integrarlo numéricamente. (Si se da por vencido, consulte la Sección 1.13.) A diferencia del último ejemplo, este no tiene una solución analítica simple en términos de funciones elementales. Se puede escribir en términos de funciones especiales (integrales elípticas) pero tienen que ser evaluadas numéricamente en cualquier caso, por lo que eso es de poca ayuda. Hago la respuesta

\[P = 2.3607 \pi \sqrt{\frac{l}{g}} . \nonumber\]

Para otro ejemplo, considere

\[\int_0^\infty \frac{dx}{x^5 \left( e^{1/x} - 1\right)}\nonumber\]

Esta integral ocurre en la teoría de la radiación de cuerpo negro. Para ayudarte a visualizar el integrando, éste y su primera derivada son cero a\(x = 0\)\(x = \infty\) y alcanza un valor máximo de\(21.201435\) at\(x = 0.201405\). La dificultad esta vez es el límite superior infinito. Pero, como en los dos ejemplos anteriores, podemos superar la dificultad haciendo un cambio de variable. Por ejemplo, si lo dejamos\(x = \tan \theta\), la integral se convierte

\[\int_0^{\pi/2} \frac{c^3 \left(c^2 + 1 \right) d\theta}{e^c - 1}, \text{where } c=\cot \theta = 1/x. \nonumber\]

El integrando es cero en ambos límites y es fácilmente calculable entre ellos, y el valor de la integral ahora puede ser calculado por la regla de Simpson de una manera sencilla. También tiene una solución analítica exacta, es decir\(\pi^4 /15\), aunque es difícil decir si es más fácil llegar a esto por análisis o por integración numérica.

Aquí hay otro:

\[\int_0^\infty \frac{x^2 dx}{(x^2+9)(x^2+4)^2} \nonumber\]

La dificultad inmediata es el límite superior infinito, pero eso se trata fácilmente haciendo un cambio de variable:\(x = \tan \theta\). La integral se convierte entonces

\[\int_{\theta=0}^{\pi/2} \frac{t(t+1)d\theta}{(t+9)(t+4)^2} \nonumber\]

en el que\(t = \tan^2 \theta\). El límite superior ahora es finito, y el integrando es fácil de calcular, excepto, quizás, en el límite superior. Sin embargo, después de alguna vacilación inicial el lector probablemente estará de acuerdo en que el integrando es cero en el límite superior. El integrand se ve así:

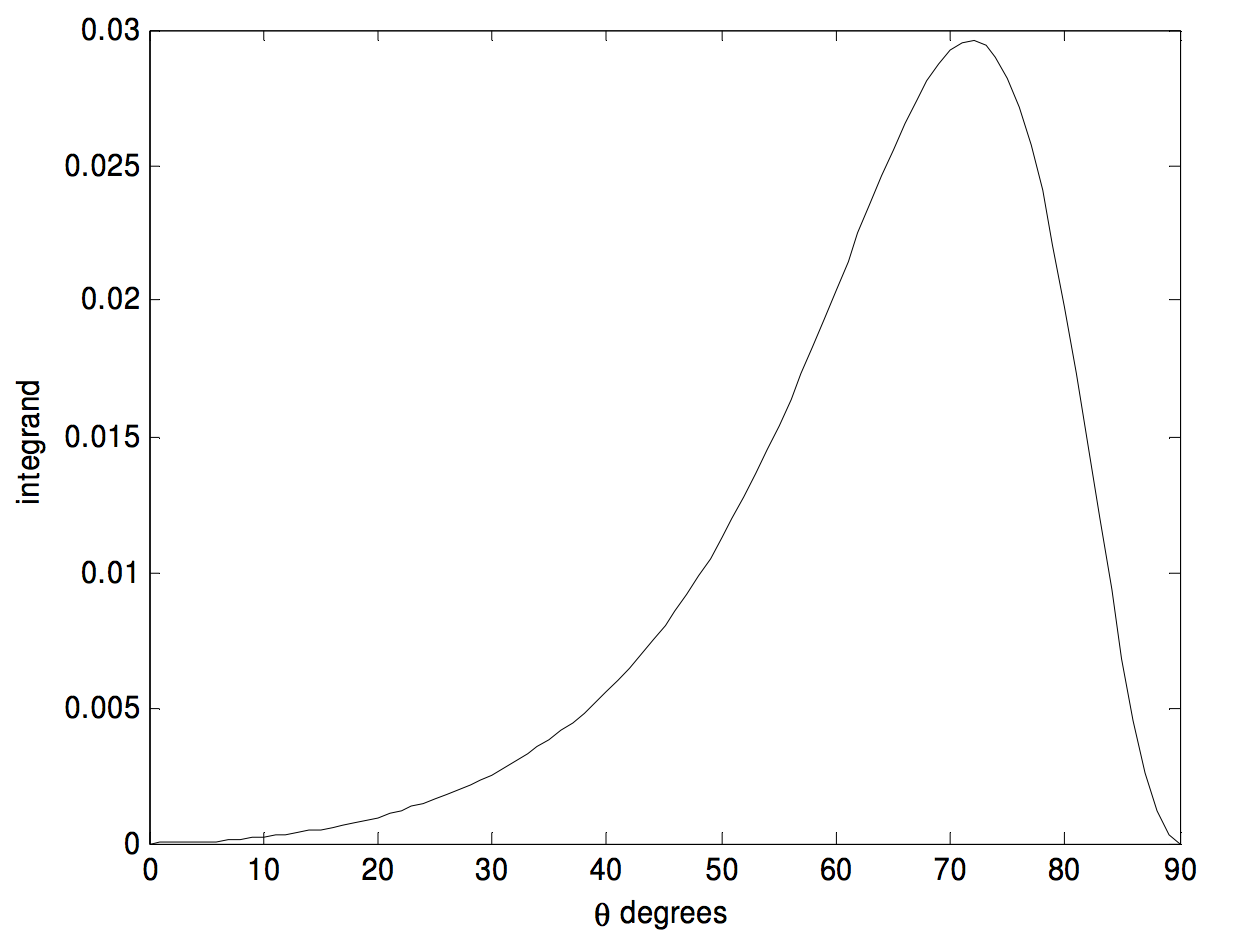
Alcanza un máximo de\(0.029 \ 5917\) at\(\theta = 71^\circ .789 \ 962\). La regla de Simpson me dio fácilmente una respuesta de\(0.015 \ 708\). La integral tiene una solución analítica (pruébalo) de\(\pi/200\).

Existen, por supuesto, métodos de integración numérica distintos a la regla de Simpson. Describo uno aquí sin pruebas. Yo lo llamo “integración de siete puntos”. Puede parecer complicado, pero una vez que lo has programado con éxito para una computadora, puedes olvidar los detalles, y a menudo es incluso más rápido y preciso que la regla de Simpson. Evalúa la función en\(6n + 1\) puntos, donde\(n\) es un entero, para que haya\(6n\) intervalos. Si, por ejemplo\(n = 4\), se evalúa la función en\(25\) puntos, incluidos los límites inferior y superior de integración. La integral es entonces:

\[\int_a^b f(x)dx = 0.3 \times (\Sigma_1 + 2 \Sigma_2 + 5 \Sigma_3 + 6\Sigma_4)δx, \label{1.2.9}\]

donde\(δx\) es el tamaño del intervalo, y

\[\Sigma_1 = f_1 + f_3 + f_5 + f_9 + f_{11} + f_{15} + f_{17} + f_{21} + f_{23} + f_{25} , \label{1.2.10}\]

\[\Sigma_2 = f_7 + f_{13} + f_{19} , \label{1.2.11}\]

\[\Sigma_3 = f_2 + f_6 + f_8 + f_{12} + f_{14} + f_{18} + f_{20} + f_{24} \label{1.2.12}\]

y\[\Sigma_4 = f_4 + f_{10} + f_{16} + f_{22} . \label{1.2.13}\]

Aquí, por supuesto,\(f_1 = f(a)\) y\(f_{25} = f(b)\). Puedes probar esto en las funciones que ya hemos integrado por regla de Simpson, y ver si es más rápido.

Intentemos una última integración antes de pasar a la siguiente sección. Vamos a probar

\[\int_0^{10} \frac{1}{1+8x^3} dx . \nonumber\]

Esto puede fácilmente (!) integrarse analíticamente, y tal vez le gustaría demostrar que es

\[\frac{1}{12} \ln \frac{147}{127} + \frac{1}{\sqrt{12}} \tan^{-1} \sqrt{507} + \frac{\pi}{\sqrt{432}} = 0.6039748 . \nonumber\]

Sin embargo, nuestro propósito en esta sección es aprender algunas habilidades de integración numérica. Usando la regla de Simpson, obtuve la respuesta anterior a siete decimales con\(544\) intervalos. Con integración de siete puntos, sin embargo, utilicé solo\(162\) intervalos para lograr la misma precisión, una reducción de\(70%\). De cualquier manera, el cálculo en una computadora rápida fue casi instantáneo. Sin embargo, si hubiera sido una integración realmente larga, la mayor eficiencia de la integración de siete puntos podría haber ahorrado horas. También vale la pena señalar que\(x \times x \times x\) es más rápido de calcular que\(x^3\). Además, si hacemos la sustitución y = 2x, la integral se vuelve

\[\int_0^{20} \frac{0.5}{1+y^3} dy . \nonumber\]

Esto reduce el número de multiplicaciones a realizar de\(489\) a\(326\) — es decir, una reducción adicional de un tercio. Pero todavía no hemos hecho lo mejor que pudimos hacer. Veamos la función\(\frac{0.5}{1+y^3}\), en la figura I.2b:

\(\text{FIGURE I2b}\)

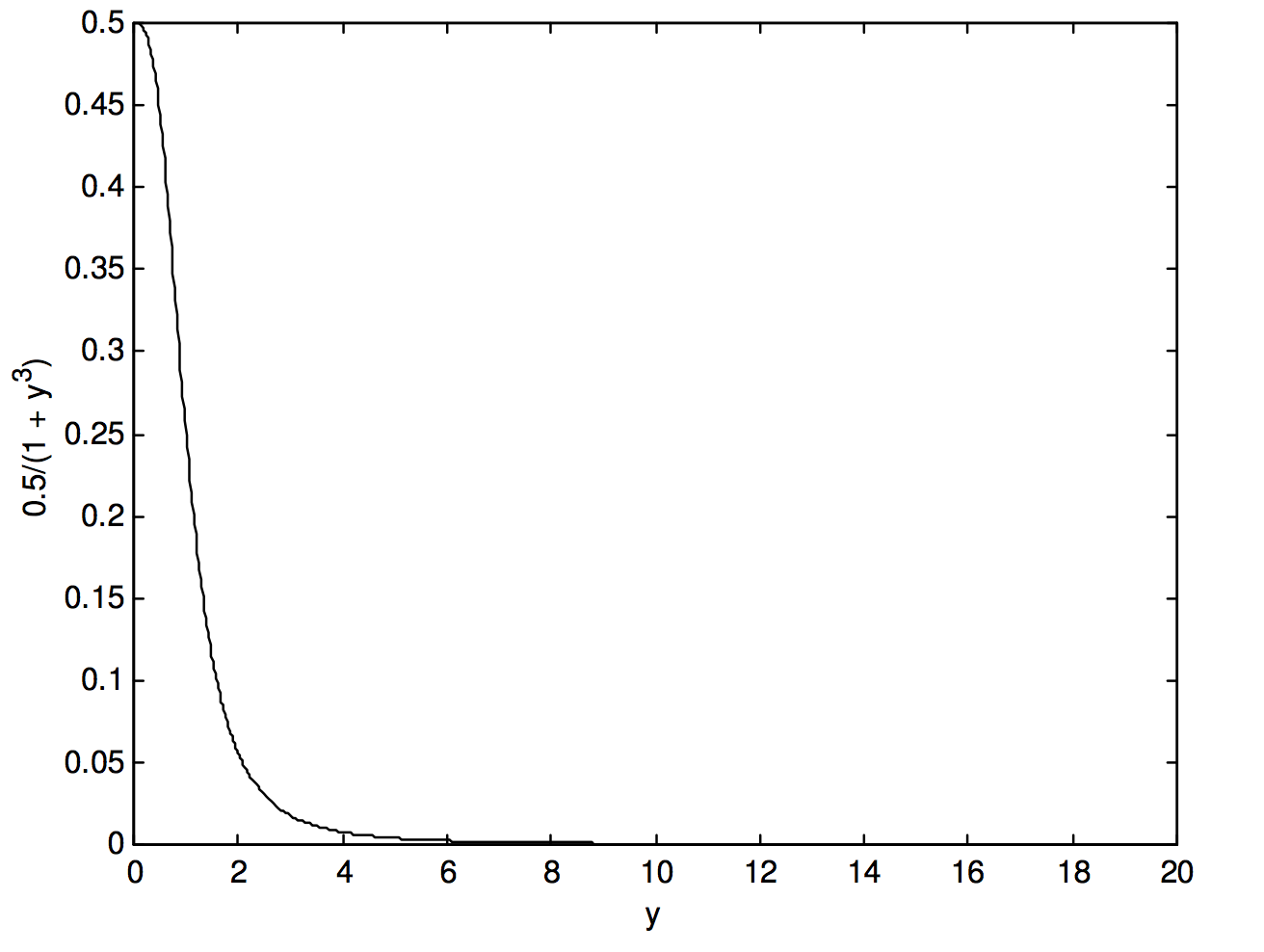
Vemos que más allá\(y = 6\), nuestros esfuerzos se han desperdiciado en gran medida. No necesitamos intervalos de integración tan finos. Encuentro que puedo obtener el mismo nivel de precisión − es decir, una respuesta de\(0.6039748\) − usando 48 intervalos de\(y = 0\) a\(6\) e\(24\) intervalos de\(y = 6\) a\(20\). Así, por diversos medios hemos reducido el número de veces que la función tuvo que ser evaluada desde nuestro original\(545\) a\(72\), así como reducir el número de multiplicaciones cada vez en un tercio, una reducción del tiempo de cómputos por\(91%\). Este último ejemplo muestra que a menudo es ventajoso usar intervalos finos de integración solo cuando la función está cambiando rápidamente (es decir, tiene una gran pendiente), y volver a intervalos más gruesos donde la función está cambiando solo lentamente.

El método de cuadratura gaussiana de integración numérica se describe en las Secciones 1.15 y 1.16.