1.4: La Solución de f (x) = 0

El título de esta sección pretende ser llamativo. Algunas ecuaciones son fáciles de resolver; otras parecen ser más difíciles. En esta sección, vamos a tratar de resolver cualquier Ecuación en toda la forma\(f(x) = 0\) (¡que cubre casi todo!) y en la mayoría de los casos tendremos éxito con facilidad.

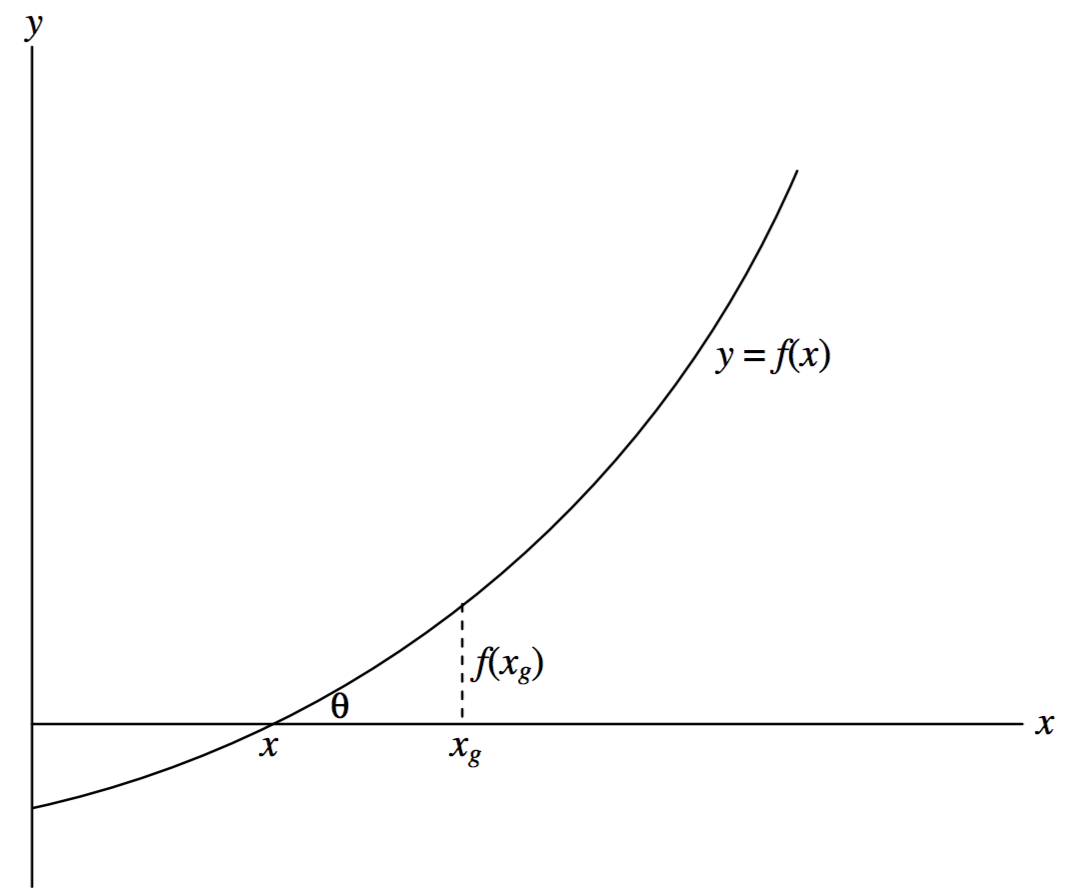
La Figura I.3 muestra una gráfica de la Ecuación\(y = f(x)\). Tenemos que encontrar el valor (o quizás valores) de\(x\) tal que\(f(x) = 0\).

Suponemos que la respuesta podría ser\(x_g\), por ejemplo. Calculamos\(f(x_g)\). No va a ser cero, porque nuestra conjetura está equivocada. La figura muestra nuestra suposición\(x_g\), el valor correcto\(x\), y\(f(x_g)\). La tangente del ángulo\(\theta\) es la derivada\(f^\prime (x)\), pero ahí no podemos calcular la derivada porque aún no sabemos\(x\). Sin embargo, podemos calcular\(f^\prime (x_g)\), que está cerca. En cualquier caso\(\tan \theta\), o\(f^\prime (x_g)\), es aproximadamente igual a\(f(x_g)/(x_g- x)\), de manera que

\[x \approx x_g - \frac{f(x_g)}{f^\prime (x_g)} \label{1.4.1}\]

estará mucho más cerca del verdadero valor de lo que era nuestra suposición original. Usamos el nuevo valor como nuestra próxima suposición, y seguimos iterando hasta

\[\left| \frac{x_g - x}{x_g} \right| \nonumber\]

es menor que cualquier precisión que deseemos. El método suele ser extraordinariamente rápido, incluso para una primera suposición salvajemente inexacta. El método se conoce como iteración Newton-Raphson. Hay algunos casos en los que el método no convergerá, y a menudo se pone énfasis en estos casos excepcionales en cursos matemáticos, dando la impresión de que el proceso de Newton-Raphson es de aplicabilidad limitada. Estos casos excepcionales, sin embargo, a menudo se inventan artificialmente para ilustrar las excepciones (de hecho citamos algunos a continuación), y en la práctica Newton-Raphson suele ser el método de elección.

\(\text{FIGURE I.3}\)

A menudo dejaré caer el subíndice torpe\(g\), y escribiré el esquema Newton-Raphson como

\[x = x - f(x) / f^\prime (x) , \label{1.4.2}\]

que significa “comenzar con algún valor de\(x\), calcular el lado derecho, y usar el resultado como un nuevo valor de\(x\)”. Se puede objetar que esto es un mal uso del\(=\) símbolo, y que lo anterior no es realmente una “Ecuación”, ya que\(x\) no puede igualar\(x\) menos algo. Sin embargo, cuando se\(x\) haya encontrado la solución correcta para, ésta va a satisfacer\(f(x) = 0\), y lo anterior es de hecho una Ecuación perfectamente buena y un uso válido del\(=\) símbolo.

Ejemplo\(\PageIndex{1}\)

Resolver la ecuación\(1/x = \ln x\)

Tenemos\(f = 1/x - \ln x = 0\)

Y\(f^\prime = -(1 + x)/ x^2\),

de la que\(x − f / f^\prime\) se convierte, después de cierta simplificación,

\[\frac{x[2 + x(1-\ln x)]}{1+x}, \nonumber\]

para que la iteración de Newton-Raphson sea

\[x = \frac{x[2 + x(1- \ln x )]}{1+x} . \nonumber\]

Queda la pregunta de cuál debería ser la primera conjetura. Sabemos (¡o deberíamos saber!) eso\(\ln 1 = 0\) y\(\ln 2 = 0.6931\), entonces la respuesta debe estar en algún lugar entre\(1\) y\(2\). Si lo intentamos\(x = 1.5\), las iteraciones sucesivas son

\ begin {array} {c}
1.735\ 081\ 403\\
1.762\ 915\ 391\\
1.763\ 222\ 798\\
1.763\ 222\ 834\\
1.763\ 222\ 835\
\ nonumber
\ end {array}

Esto convergió rápidamente desde una primera suposición bastante buena de\(1.5\). Muy a menudo la iteración de Newton-Raphson convergerá, incluso rápidamente, a partir de una primera suposición muy estúpida, pero en este ejemplo en particular hay límites a la estupidez, y al lector le gustaría probar que, para lograr la convergencia, la primera conjetura debe estar en el rango

\[0 < x < 4.319 \ 136 \ 566 \nonumber\]

Ejemplo\(\PageIndex{2}\)

Resolver la ecuación improbable\(\sin x = \ln x\)

Tenemos\(f = \sin x - \ln x\) y\(f^\prime = \cos x - 1/x\),

y después de alguna simplificación la iteración de Newton-Raphson se convierte en

\[x = x \left[ 1 + \frac{\ln x - \sin x}{x \cos x -1} \right] . \nonumber\]

Gráficas de\(\sin x\) y\(\ln x\) proporcionarán una primera conjetura, pero en lugar de eso y sin tener mucha idea de cuál podría ser la respuesta, podríamos intentar una bastante estúpida\(x = 1\). Las iteraciones posteriores producen

\ begin {array} {c}
2.830\ 487\ 722\\
2.267\ 902\ 211\
2.219\ 744\ 452\\
2.219\ 107\ 263\
2.219\ 107\ 149\\
2.219\ 107\ 149\ 107\ 149\
\ nonumber
\ end {array}

Ejemplo\(\PageIndex{3}\)

Resuelve la Ecuación\(x^2 = a\) (¡Una nueva forma de encontrar raíces cuadradas!)

\[ f= x^2 - a, \quad f^\prime = 2x. \nonumber\]

Después de un poco de simplificación, el proceso de Newton-Raphson se convierte en

\[x = \frac{x^2 + a}{2x}. \nonumber\]

Por ejemplo, ¿cuál es la raíz cuadrada de 10? Adivina 3. Las iteraciones posteriores son

\ begin {array} {c}
3.166\ 666\ 667\\
3.162\ 280\ 702\\
3.162\ 277\ 661\\
3.162\ 277\ 661\
\ nonumber
\ end {array}

Ejemplo\(\PageIndex{4}\)

Resolver la Ecuación\(ax^2 + bx + c = 0\) (¡una nueva forma de resolver ecuaciones cuadráticas!)

\[f = ax^2 + bx + c = 0, \nonumber\]

\[f^\prime = 2ax + b . \nonumber\]

Newton-Raphson:

\[x = x- \frac{ax^2 + bx + c}{2ax + b}, \nonumber\]

que se convierte, tras la simplificación,

\[x = \frac{ax^2-c}{2ax+b}. \nonumber\]

Esta es solo la iteración dada en la sección anterior, sobre la solución de Ecuaciones cuadráticas, y muestra por qué el método anterior convergió tan rápidamente y también cómo llegué realmente a la Ecuación (que fue a través del proceso de Newton-Raphson, ¡y no sumando arbitrariamente\(ax^2\) a ambos lados!)