1.12: Ajuste de una línea recta de mínimos cuadrados a un conjunto de puntos de observación

Muy a menudo tenemos un conjunto de puntos observacionales\((x_i , y_i), \ i = 1\) a\(N\), que parecen caer aproximadamente pero no del todo en línea recta, y deseamos trazar la “mejor” línea recta que pase lo más cerca posible de todos los puntos. Incluso las calculadoras manuales científicas más pequeñas en estos días tienen programas para hacer esto —pero es bueno entender con precisión qué es lo que se está calculando.

Muy a menudo los valores de\(x_i\) se conocen “exactamente” (o al menos a un alto grado de precisión) pero hay errores apreciables en los valores de\(y_i\). En la figura\(\text{I.6B}\) muestro un conjunto de puntos y una línea recta plausible que pasa cerca de los puntos.

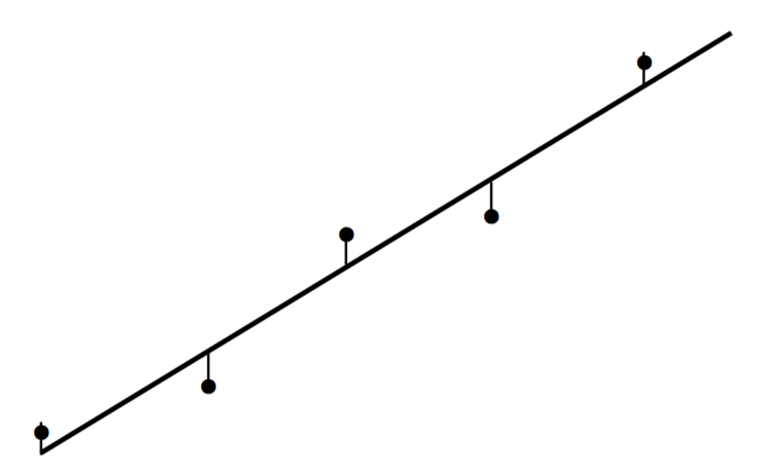
\(\text{FIGURE I.6B}\)

También se dibujan las distancias verticales desde cada punto desde la línea recta; estas distancias son los residuos de cada punto.

Es habitual elegir como la “mejor” línea recta esa línea de tal manera que la suma de los cuadrados de estos residuos sea menor. Bien puede preguntarse si podría tener al menos el mismo sentido elegir como la “mejor” línea recta esa línea de tal manera que la suma de los valores absolutos de los residuales sea menor. Eso ciertamente sí tiene sentido, y en algunas circunstancias puede incluso ser la línea apropiada para elegir. Sin embargo, la línea recta de “mínimos cuadrados” es bastante más fácil de calcular y es fácilmente susceptible de análisis estadístico. Tenga en cuenta también que el uso de las distancias verticales entre los puntos y la línea recta es apropiado solo si los valores de\(x_i\) son conocidos con una precisión mucho mayor que los valores de\(y_i\). En la práctica, este suele ser el caso —pero no siempre es así, en cuyo caso esta no sería la “mejor” línea apropiada para elegir.

La línea así descrita, es decir, la línea tal que la suma de los cuadrados de los residuos verticales es menor a menudo se llama vagamente la “línea recta de mínimos cuadrados”. Técnicamente, es la regresión lineal de mínimos cuadrados de\(y\) upon\(x\). Podría ser bajo algunas circunstancias que son los valores de los\(y_i\) que se conocen con gran precisión, mientras que puede haber errores apreciables en el\(x_i\). En ese caso queremos minimizar la suma de los cuadrados de los residuos horizontales, y luego calculamos la regresión lineal de mínimos cuadrados de\(x\) upon\(y\). Una vez más, podemos tener una situación en la que los errores en\(x\) y\(y\) son comparables (no necesariamente exactamente iguales). En ese caso podemos querer minimizar la suma de los cuadrados de los residuos perpendiculares de los puntos de la línea. Pero luego hay una dificultad de dibujar los\(y\) ejes\(x\) - y -a escalas iguales, lo que sería problemático si, por ejemplo,\(x\) fueran un tiempo y\(y\) una distancia.

Para empezar, sin embargo, asumiremos que los errores en\(x\) son insignificantes y queremos calcular la regresión de mínimos cuadrados de\(y\) on\(x\). También haremos la suposición de que todos los puntos tienen el mismo peso. Si no lo hacen, esto se trata fácilmente de manera obvia; así, si un punto tiene el doble de peso que otros puntos, simplemente cuente ese punto dos veces.

Entonces, supongamos que tenemos\(N\) puntos,\((x_i , y_i)\),\(i = 1\) a\(N\), y deseamos encajar una línea recta que se acerque lo más posible a todos los puntos. Deja que la línea sea\(y=a_1 x + a_0\). El residuo\(R_i\) del punto\(i\) th es

\[R_i = y_i - (a_1 x_i + a_0) . \label{1.12.1} \tag{1.12.1}\]

Tenemos ecuaciones lineales\(N\) simultáneas de este tipo para las dos incógnitas\(a_1\) y\(a_0\), y, para la regresión de mínimos cuadrados de\(y\) sobre\(x,\) tenemos que encontrar los valores de\(a_1\) y\(a_0\) tal que la suma de los cuadrados de los residuos sea menor. Ya sabemos cómo hacerlo desde la Sección 1.8, por lo que se soluciona el problema. (Solo asegúrate de entender que, en la Sección 1.8 estábamos usando\(x\) para las incógnitas y\(a\) para los coeficientes; ¡aquí estamos haciendo lo contrario!)

Ahora para un Ejercicio. Supongamos que nuestros puntos son los siguientes:

\ begin {array} {c c}
x & y\\
\\
1 & 1.00\\
2 & 2.50\\
3 & 2.75\\
4 & 3.00\\
5 & 3.50\\
\ end {array}

i.) Dibuja estos puntos en una hoja de papel cuadriculado y, usando tu ojo y una regla, dibuja lo que creas que es la mejor línea recta que pasa cerca de estos puntos.

ii.) Escribir un programa de computadora para calcular la regresión de mínimos cuadrados de\(y\) upon\(x\). Tienes que hacer esto tarde o temprano, así que bien podrías hacerlo ahora. De hecho ya deberías (después de leer la Sección 1.8) haber escrito un programa para resolver\(N\) Ecuaciones en\(n\) incógnitas, así que solo incorporas ese programa a esto.

iii.) Ahora calcula la regresión de mínimos cuadrados de\(y\) sobre\(x\). Yo lo hago\(y = 0.55x + 0.90\). ¡Dibuja esto en tu papel cuadriculado y mira lo cerca que estaba tu estimación de ojos y regla!

iv.) ¿Cómo va a calcular la regresión de mínimos cuadrados de\(x\) upon\(y\)? ¡Fácil! Solo usa el mismo programa, pero lee los\(x\) valores -para\(y\) y los\(y\) -valores para\(x\)! ¡No hace falta escribir un segundo programa! Yo lo hago\(y = 0.645x + 0.613\). Dibuja eso en tu papel cuadriculado y mira cómo se compara con la regresión de\(y\) upon\(x\).

Las dos líneas de regresión se cruzan en el centroide de los puntos, que en este caso se encuentra en (3.00, 2.55). Si los errores en\(x\) y\(y\) son comparables, una mejor línea razonable podría ser aquella que pasa por el centroide, y cuya pendiente es la media (¿aritmética? geométrica?) de las regresiones de\(y\) un\(x\) y\(x\) otro\(y\). Ahora bien, en la Sección 1.12 voy a hacer referencia a dónde se trata más a fondo esta cuestión.

Si las regresiones de\(y\) sobre\(x\) y\(x\) sobre\(y\) son respectivamente\(y = a_1 x + a_0\) y\(y = b_1 x + b_0\), la cantidad\(\sqrt{a_1/b_1}\) se denomina coeficiente de correlación r entre las variables x e y. Si los puntos están exactamente en línea recta, el coeficiente de correlación es 1. El coeficiente de correlación se utiliza a menudo para mostrar qué tan bien, o qué tan mal, se correlacionan dos variables, y a menudo se afirma que están altamente correlacionadas si\(r\) está cerca de 1 y solo débilmente correlacionadas si\(r\) está cerca de cero. No tengo la intención de empantanarme en las estadísticas formales en este capítulo, pero aquí está en orden una palabra de advertencia. Si solo tienes dos puntos, necesariamente están en línea recta, y el coeficiente de correlación es necesariamente 1 —pero no hay evidencia alguna que sea de que las variables estén correlacionadas de alguna manera. El coeficiente de correlación por sí mismo no indica cuán estrechamente correlacionadas están dos variables. La significancia del coeficiente de correlación depende del número de puntos, y la significancia es algo que se puede calcular numéricamente mediante pruebas estadísticas precisas.