1.13: Ajuste de un polinomio de mínimos cuadrados a un conjunto de puntos de observación

Comenzaré asumiendo que los valores de x son conocidos con un alto grado de precisión, y todos los errores están en los valores de\(y\). Es decir, calcularé una regresión polinomial de mínimos cuadrados de\(y\) sobre\(x\). De hecho voy a mostrar cómo calcular una regresión cuadrática de mínimos cuadrados de\(y\) sobre\(x\), un polinomio cuadrático que representa, por supuesto, una parábola. Lo que queremos hacer es calcular los coeficientes de\(a_0, \ a_1, \ a_2\) tal manera que la suma de los cuadrados del residuo sea menor, siendo el residual del punto\(i\) th

\[R_i = y_i - (a_0 + a_1 x_i + a_2 x_1^2 ). \label{1.13.1} \tag{1.13.1}\]

Tienes ecuaciones lineales\(N\) simultáneas de este tipo para las tres incógnitas\(a_0, \ a_1\) y\(a_2\). Ya sabes cómo encontrar la solución de mínimos cuadrados para estos, y de hecho, después de haber leído la Sección 1.8, ya tienes un programa para resolver las Ecuaciones. (Recuerda que aquí están las incógnitas\(a_0, \ a1\) y\(a_2\) —\(x\) ¡no! Sólo tienes que ajustar un poco tu notación.) Por lo tanto, no hay dificultad para encontrar la regresión cuadrática de mínimos cuadrados de\(y\) sobre\(x\), y de hecho la extensión a polinomios de mayor grado ahora será obvia.

Como Ejercicio, aquí hay algunos puntos que recientemente tuve en una aplicación real:

\ begin {array} {c c}
x & y\\
395.1 & 171.0\\
448.1 & 289.0\\
517.7 & 399.0\\
583.3 & 464.0\\
790.2 & 620.0\
\ end {array}

Dibuja estos en una hoja de papel cuadriculado y dibuja a mano una bonita curva suave pasando lo más cerca posible del punto. Ahora calcula la parábola de mínimos cuadrados (regresión cuadrática de\(y\) sobre\(x\)) y mira qué tan cerca estabas. Yo lo hago\(y = -961.34 + 3.7748x - 2.247 \times 10^{-3} x^2\). Se muestra en la Figura\(\text{I.6C}\).

Ahora les dejo para que resuelvan cómo ajustar una regresión cúbica de mínimos cuadrados (o de hecho cualquier polinomio) de\(y\) on\(x\) a un conjunto de puntos de datos. Para los datos anteriores, hago que el ajuste cúbico sea

\[y = -2537.605 + 12.4902x - 0.017777x^2 + 8.89 \times 10^{-6} x^3.\]

Esto se muestra en la Figura\(\text{I.6D}\), y, en la escala de este dibujo no se puede distinguir (dentro del rango cubierto por\(x\) en la figura) de la Ecuación cuártica que pasaría exactamente por los cinco puntos.

La curva cúbica es un ajuste “mejor” que la curva cuadrática o una línea recta en el sentido de que, cuanto mayor sea el grado de polinomio, más cerca está el ajuste y menos los residuos. Pero los polinomios de grado superior tienen más “meneo”, y hay que preguntarse si un polinomio de alto grado con muchos “meneo” es realmente un ajuste realista, y tal vez debería estar satisfecho con un ajuste cuadrático. Sobre todo, es importante entender que es muy peligroso usar la curva que has calculado para extrapolar más allá del rango\(x\) para el que tienes datos —y esto es especialmente cierto en el caso de los polinomios de mayor grado.

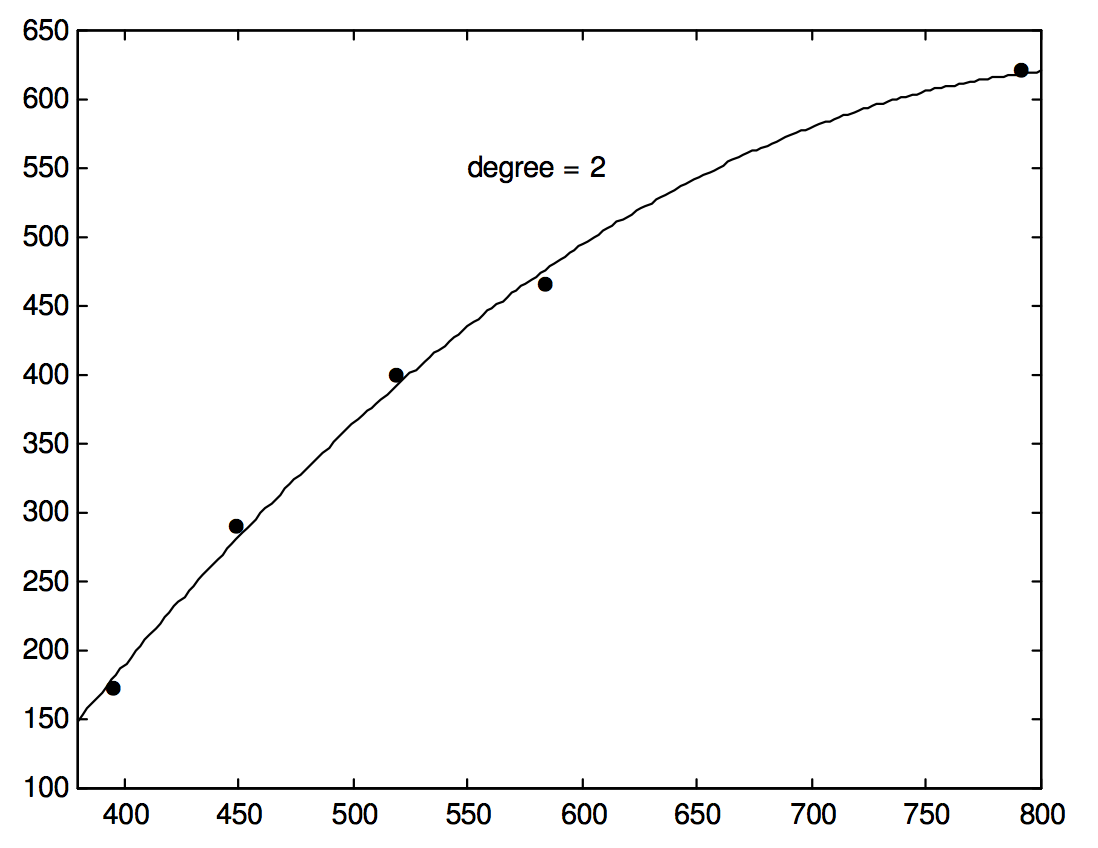
\(\text{FIGURE I.6C}\)

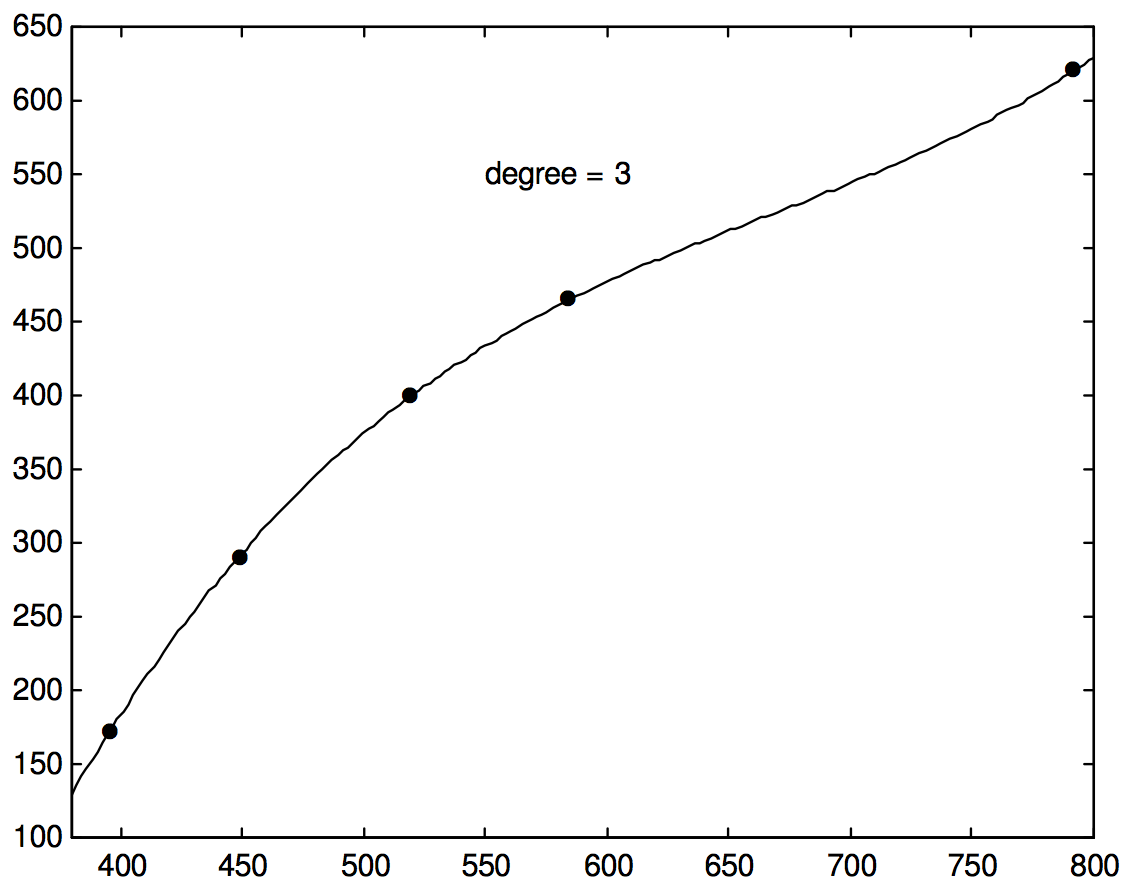
\(\text{FIGURE I.6D}\)

¿Qué sucede si los errores en no\(x\) son despreciables, y los errores en\(x\) y\(y\) son comparables en tamaño? En ese caso se quiere trazar una gráfica de\(y\) contra\(x\) en una escala tal que la unidad para\(x\) sea igual a la desviación estándar de los\(x\) -residuos del polinomio elegido y la unidad para\(y\) es igual a la desviación estándar de los\(y\) -residuos de la polinomio elegido. Para un relato detallado y minucioso de cómo hacer esto, le remito a un artículo de D. York en Canadian Journal of Physics, 44, 1079 (1966).