1.14: Polinomios de Legendre

Última actualización
Guardar como PDF

Page ID: 131198

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Considera la expresión

\[(1-2rx + r^2 ) ^{-1/2} , \label{1.14.1} \tag{1.14.1}\]

en los que\(|x|\) y\(|r|\) son ambos menores o iguales a uno. Expresiones similares a esta ocurren con bastante frecuencia en la física teórica, por ejemplo en el cálculo de los potenciales gravitacionales o electrostáticos de cuerpos de forma arbitraria. Véase, por ejemplo, el Capítulo 5, Secciones 5.11 y 5.12.

Ampliar la expresión\(\ref{1.14.1}\) por el teorema binomial como una serie de poderes de\(r\). Esto es sencillo, aunque no particularmente fácil, y se podría esperar pasar varios minutos en obtener los coeficientes de las primeras potencias de\(r\). Encontrarás que el coeficiente de\(r^l\) es una expresión polinómica en\(x\) de grado\(l\). De hecho, la expansión toma la forma

\[(1 - 2rx + r^2 )^{-1/2} = P_0 (x) + P_1 (x) r + P_2 (x) r^2 + P_3 (x) r^3 ... \label{1.14.2} \tag{1.14.2}\]

Los coeficientes de la potencia sucesiva de\(r\) son los polinomios de Legendre; el coeficiente de\(r^l\), que es\(P_l(x)\), es el polinomio de Legendre de orden\(l\), y es un polinomio en\(x\) incluir términos tan altos como\(x^l\). Introducimos estos polinomios en esta sección porque los necesitaremos en la Sección 1.15 sobre la derivación de la Cuadratura Gaussiana.

Si has tratado concienzudamente de expandir la expresión\(\ref{1.14.1}\), habrás encontrado que

\[P_0 (x) = 1, \quad P_1 (x) = x, \quad P_2 (x) = \frac{1}{2} (3x^2 - 1), \label{1.14.3} \tag{1.14.3}\]

aunque probablemente te diste por vencido con el agotamiento después de eso y no lo llevaste más lejos. Si miras detenidamente cómo derivaste los primeros polinomios, es posible que hayas descubierto por ti mismo que puedes obtener el siguiente polinomio en función de dos polinomios anteriores. Incluso puede haber descubierto por sí mismo la siguiente relación de recursión:

\[P_{l+1} = \frac{(2l+1)xP_l - lP_{l-1}}{l+1}. \label{1.14.4} \tag{1.14.4}\]

Esto nos permite obtener rápidamente polinomios Legendre de orden superior, ya sea numéricamente o en forma algebraica. Por ejemplo, poner\(l = 1\) y mostrar que la Ecuación 1.12.4 resulta en\(P_2 = \frac{1}{2} (3x^2 - 1)\). Entonces querrás calcular\(P_3\), y luego\(P_4\), y cada vez más y más. Otra forma de generarlos es formar la Ecuación

\[P_{l+1} = \frac{1}{2^l l!} \frac{d^l}{dx^l} (x^2 - 1)^l . \label{1.14.5} \tag{1.14.5}\]

Aquí están los primeros once polinomios de Legendre:

\ begin {array} {l}
P_0 = 1\\
P_1 = x\\
P_2 =\ frac {1} {2} (3x^2 - 1)\\
P_3 =\ frac {1} {2} (5x^3 - 3x)\\
P_4 =\ frac {1} {8} (35x^4 - 30x^2 + 3)\
P__5 =\ frac {1} {16} (63x^5 - 70x^3 + 15x)\\
P_6 =\ frac {1} {16} ( 231x^6 - 315x^4 + 105x^2 - 5)\\
P_7 =\ frac {1} {16} (429x^7 - 693x^5 + 315x^3 -35x)\\
P_8 =\ frac {1} {128} (6435x^8 - 12012x^6 + 6930x^4 -1260x^2 + 35\
P_9 =\ frac {1} {128} (12155x^9 - 25740x^7 + 18018x^5 - 4620x^3 + 315x)\\
P_ {10} =\ frac {1} {256} ( 46189 x^ {10} - 109395x^8 + 90090x^6 - 30030x^4 + 3465x^2 - 63)\
\ etiqueta {1.14.6}\ tag {1.14.6}
\ end {array}

Los polinomios con argumento\(\cos \theta\) se dan en la Sección 5.11 del Capítulo 5.

En lo que sigue en la siguiente sección, también vamos a querer conocer las raíces de las Ecuaciones\(P_l = 0\) para\(l > 1\). La inspección de las formas de estos polinomios mostrará rápidamente que todos los polinomios impares tienen una raíz de cero, y todas las raíces distintas de cero ocurren en pares positivos/negativos. Habiendo leído las Secciones 1.4 y 1.5, no tendremos dificultad para encontrar las raíces de estas Ecuaciones. Las raíces\(x_{l,i}\) se encuentran en la siguiente tabla, en la que también se enumeran ciertos coeficientes\(c_{l,i}\), que se explicarán en la Sección 1.15.

Raíces de\(P_l = 0\)

\ begin {array} {c c c}
l & x_ {l, i} & c_ {l, i}\
\\\
2 &\ pm 0.577\ 350\ 269\ 190 & 1.000\ 000\ 000\ 00
\\\
3 &\ pm 0.774\ 596\ 669\ 241 & 0.555\ 555\ 56\\
& 0.000\ 000\ 000\ 000 & 0.888\ 888\ 89\\\
\
4 &\ pm 0.861\ 136\ 311\ 594 & 0.347\ 854\ 845\ 14\
&\ pm 0.339\ 981\ 043\ 585 & 0.652\ 145\ 154\ 86\\
\
5 &\ pm 0.906\ 179\ 845\ 939 & 0.236\ 926\ 885\ 06\\
&\ pm 0.538\ 469\ 310\ 106 & 0.478\ 628\ 670\ 50\\
& 0.000\ 000\ 000 & 0.568\ 888\ 888\ 89\\
\
6 &\ pm 0.932\ 469\ 514\ 203 & 0.171\ 324\ 492\ 38\
&\ pm 0.661\ 209\ 386\ 466 & 0.360\ 761\ 573\ 05\\
&\ pm 0.238\ 619\ 186\ 083 & 0.467\ 913\ 934\ 57\
\\
7 &\ pm 0.949\ 107\ 912\ 343 & 0.129\ 484\ 966\ 17\
&\ pm 0.741\ 531\ 185\ 599 & 0.279\ 705\ 391\ 49\
&\ pm 0.405\ 845\ 151\ 377 & 0.381\ 830\ 050\\
& 0.000\ 000\ 000\ 000 & 0.417\ 959\ 183\ 68\\
\
8 &\ pm 0.960\ 289\ 856\ 498 & 0.101\ 228\ 536\ 29\
&\ pm 0.796\ 666\ 477\ 414 & 0.222 \ 381\ 034\ 45\
&\ pm 0.525\ 532\ 409\ 916 & 0.313\ 706\ 645\ 88\
&\ pm 0.183\ 434\ 642\ 496 & 0.362\ 683\ 783\ 38\
\\
9 &\ pm 0.968\ 160\ 239\ 508 & 0.081\ 274\ 388\ 36\
&\ pm 0 .836\ 031\ 107\ 327 & 0.180\ 648\ 160\ 69\
&\ pm 0.613\ 371\ 432\ 701 & 0.260\ 610\ 696\ 40\
&\ pm 0.324\ 253\ 423\ 404 & 0.312\ 347\ 077\ 04\\
& 0.000\ 000\ 000 & 0.330\ 239\ 355\ 00\
\ \
10 &\ pm 0.973\ 906\ 528\ 517 & 0.066\ 671\ 343\ 99\\
&\ pm 0.865\ 063\ 366\ 689 & 0.149\ 451\ 349\ 64\
&\ pm 0.679\ 409\ 568\ 299 & 0.219\ 086\ 362\ 24\
&\ pm 0.433\ 395\ 394\ 129 & 0.269\ 266\ 719\ 47\
&\ pm 0.148\ 874\ 338\ 982 & 0.295\ 524\ 224\ 66\\
\
11 &\ pm 0.978\ 228\ 658\ 146 & 0.055\ 668\ 567\ 12\
&\ pm 0.887\ 062\ 599\ 768 & 0.125\ 580\ 369\ 46\\
&\ pm 0. 730\ 152\ 005\ 574 & 0.186\ 290\ 210\ 93\
&\ pm 0.519\ 096\ 129\ 207 & 0.233\ 193\ 764\ 59\\
&\ pm 0.269\ 543\ 155\ 952 & 0.262\ 804\ 544\ 51\\
& 0.000\ 000\ 000 & 0.272\ 925\ 086\ 78\
\\
12 &\ pm 0.981\ 560\ 634\ 247 & 0.047\ 175\ 336\ 39\
&\ pm 0.904\ 117\ 256\ 370 & 0.106\ 939\ 325\ 99\
&\ pm 0.769\ 902\ 674\ 194 & 0.160\ 078\ 328\ 54\
&\ pm 0.587\ 317\ 954\ 287 & 0.203\ 167\ 426\ 72\
&\ pm 0.367\ 831\ 498\ 998 & 0.233\ 492\ 536\ 54\
&\ pm 0.125\ 233\ 408\ 511 & 0.249\ 147\ 045\ 81\
\\
13 &\ pm 0.984\ 183\ 054\ 719 & 0.040\ 484\ 004\ 77\
&\ pm 0. 917\ 598\ 399\ 223 & 0.092\ 121\ 499\ 84\
&\ pm 0.801\ 578\ 090\ 733 & 0.138\ 873\ 510\ 22\
&\ pm 0.642\ 349\ 339\ 440 & 0.178\ 145\ 980\ 76\
&\ pm 0.448\ 492\ 751\ 036 & 0.207\ 816\ 047\ 54\
&\ pm 0.230\ 458\ 315\ 955 & 0.226\ 283\ 180\ 26\\
& 0.000\ 000\ 000 & 0.232\ 551\ 553\ 23\\
\
14 &\ pm 0.986\ 283\ 808\ 697 & 0.035\ 119\ 460\ 33\
&\ pm 0.928\ 434\ 883\ 664 & 0.080 \ 158\ 087\ 16\
&\ pm 0.827\ 201\ 315\ 070 & 0.121\ 518\ 570\ 69\
&\ pm 0.687\ 292\ 904\ 812 & 0.157\ 203\ 167\ 16\
&\ pm 0.515\ 248\ 636\ 358 & 0.185\ 538\ 397\ 48\
&\ pm 0.319\ 112\ 368\ 928 & 0.205\ 198\ 463\ 72\\
&\ pm 0.108\ 054\ 948\ 707 & 0.215\ 263\ 853\ 46\
\\
15 &\ pm 0.987\ 992\ 518\ 020 & 0.030\ 753\ 242\ 00\
&\ pm 0.937\ 273\ 392\ 401 & 0.070\ 366\ 047\ 49\
&\ pm 0.848\ 206\ 583\ 410 & 0.107\ 159\ 220\ 47\
&\ pm 0.724\ 417\ 731\ 360 & 0.139\ 570\ 677\ 93\
&\ pm 0.570\ 972\ 172\ 609 & 0.166\ 269\ 205\ 82\
&\ pm 0.394\ 151\ 347\ 078 & 0.186\ 161 \ 000\ 02\\
&\ pm 0.201\ 194\ 093\ 997 & 0.198\ 431\ 485\ 33\\
& 0.000\ 000\ 000 & 0.202\ 578\ 241\ 92\\
\
16 &\ pm 0.989\ 400\ 934\ 992 & 0.027\ 152\ 459\ 41\
&\ pm 0.944\ 575\ 023\ 073 & 0.062\ 253\ 523\ 94\
&\ pm 0.865\ 631\ 202\ 388 & 0.095\ 158\ 511\ 68\
&\ pm 0.755\ 404\ 408\ 355 & 0.124\ 628\ 971\ 26\
&\ pm 0.617\ 876\ 244\ 403 & 0.149\ 595\ 988\ 82\
& ;\ pm 0.458\ 016\ 777\ 657 & 0.169\ 156\ 519\ 39\\
&\ pm 0.281\ 603\ 550\ 779 & 0.182\ 603\ 415\ 04\\
&\ pm 0.095\ 012\ 509\ 838 & 0.189\ 450\ 610\ 46\
\\
17 &\ pm 0.990\ 575\ 475\ 315 & 0.024\ 148\ 302\ 87\
&\ pm 0.950\ 675\ 521\ 769 & 0.055\ 459\ 529\ 38\
&\ pm 0.880\ 239\ 153\ 727 & 0.085\ 036\ 148\ 32\
&\ pm 0.781\ 514\ 003\ 897 & 0.111\ 883\ 847\ 19\
&\ pm 0.657\ 671\ 159\ 217 & 0.135\ 136\ 368\ 47\
&\ pm 0.512\ 690\ 537\ 086 & 0.154\ 045\ 761\ 08\
&\ pm 0.351\ 231\ 763\ 454 & 0.168\ 004\ 102\ 16\
&\ pm 0.178\ 484\ 181\ 496 & 0.176\ 562\ 705\ 37\\
& 0.000\ 000\ 000 & 0.179\ 446\ 470\ 35\\
\ end {array}

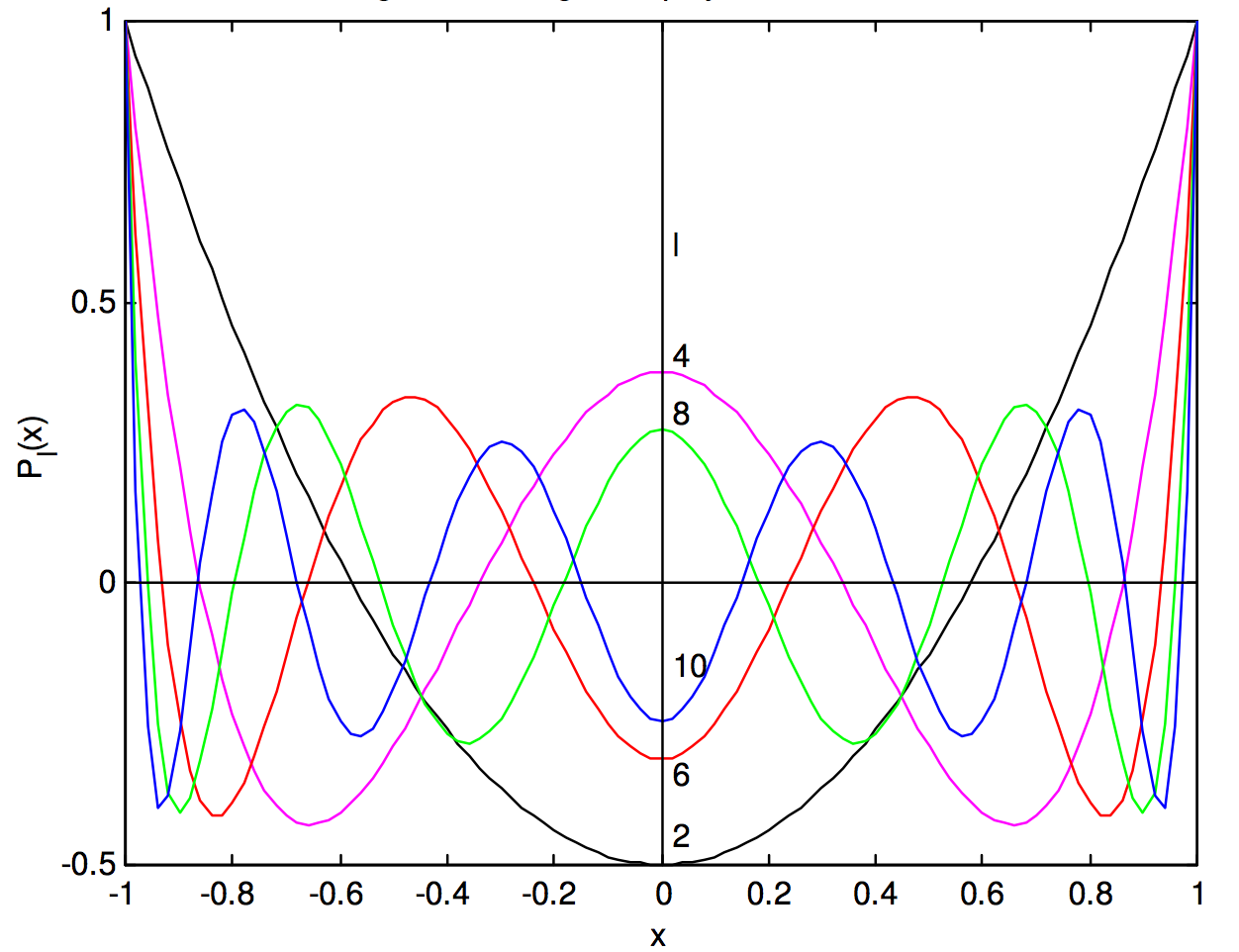
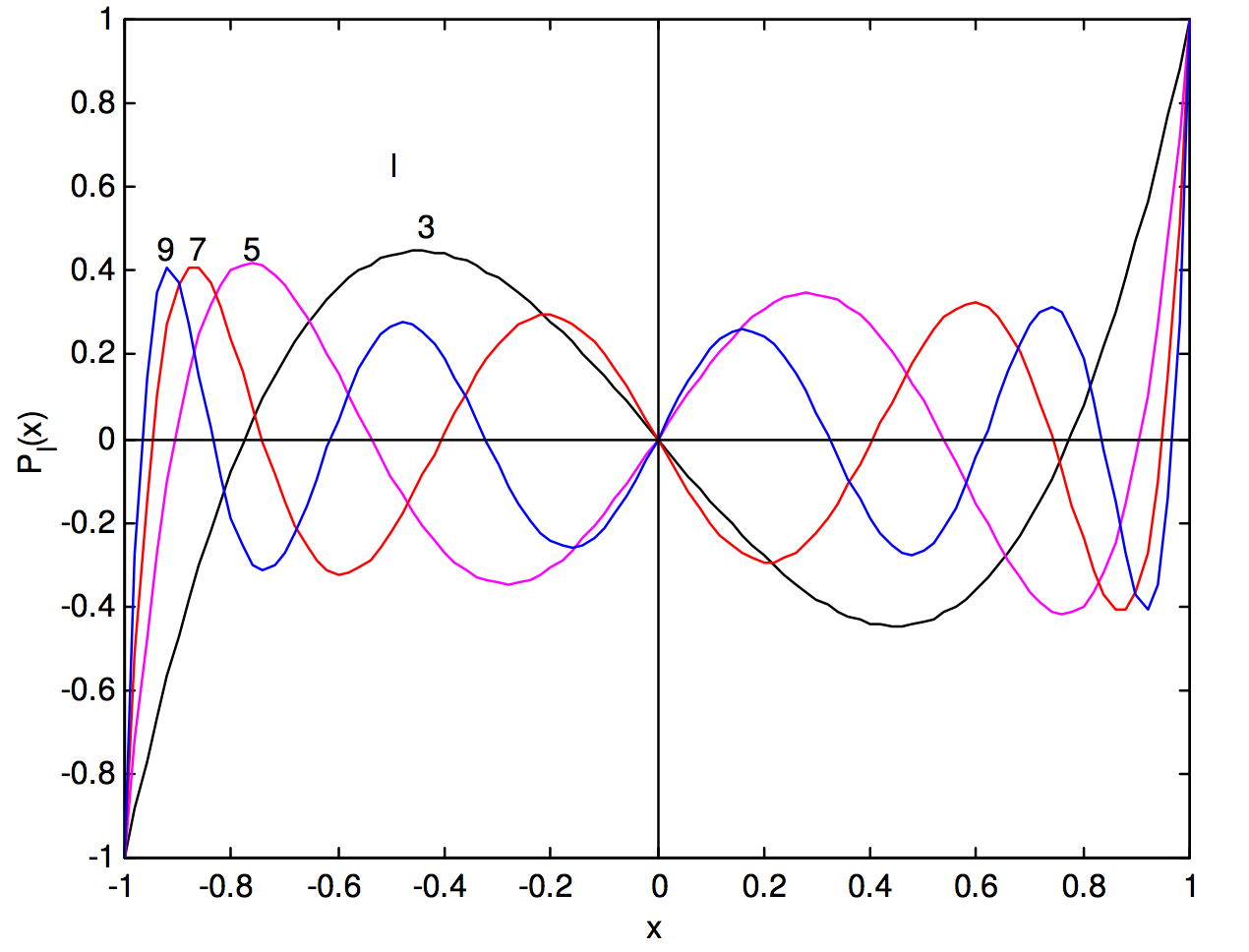
Por interés, dibujo gráficas de los polinomios de Legendre en cifras\(\text{I.7}\) y\(\text{I.8}\).

Figura\(\text{I.7}\). Polinomios de Legendre para par\(\text{I}\)
alt

Figura\(\text{I.8}\). Polinomios de Legendre para impar\(\text{I}\)
alt

Para mayor interés, debería ser fácil verificar, por sustitución, que los polinomios de Legendre son soluciones de la Ecuación diferencial

\[(1-x^2)y^{\prime \prime} - 2xy^\prime + l(l+1) y = 0. \label{1.14.7} \tag{1.14.7}\]

Los polinomios de Legendre son soluciones de esto y ecuaciones relacionadas que aparecen en el estudio de las vibraciones de una esfera sólida (armónicos esféricos) y en la solución de la Ecuación de Schrödinger para átomos similares a hidrógeno, y juegan un papel importante en la mecánica cuántica.