2.7: Ajuste de una sección cónica a través de cinco puntos

\(\text{FIGURE II.38}\)

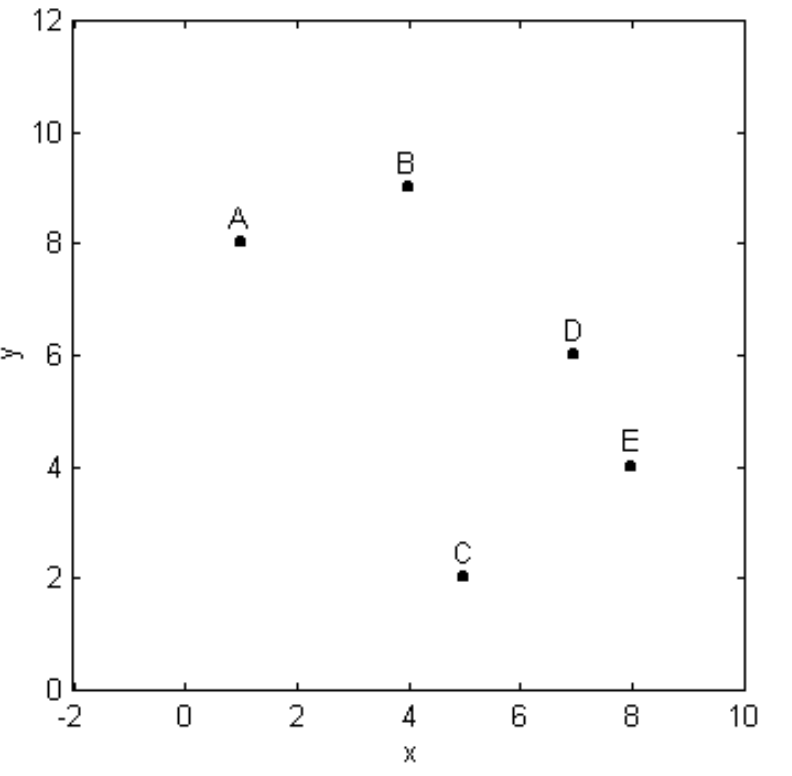
En la\(\text{II.38}\) figura se muestran los cinco puntos\(\text{A}(1,8), \ \text{B}(4,9), \ \text{C}(5,2), \ \text{D}(7,6), \ \text{E}(8,4)\). Problema: Dibuja una sección cónica a través de los cinco puntos.

Lo primero que hay que notar es que, dado que una sección cónica es de la forma

\[ax^2 + 2hxy + by^2 + 2gx + 2fy + 1 = 0 \label{2.8.1} \tag{2.8.1}\]

(recuerda que no hay pérdida de generalidad al tomar el término constante como 1), cinco puntos son necesarios y suficientes para definir una sección cónica de manera única. Una y sólo una sección cónica se puede dibujar a través de estos cinco puntos. Sólo tenemos que determinar los cinco coeficientes. La forma más directa (pero no la más rápida ni eficiente) de hacerlo es sustituir cada uno de los pares (x, y) en la Ecuación a su vez, obteniendo así cinco Ecuaciones lineales en los cinco coeficientes.

Hay una mejor manera.

Anotamos las Ecuaciones para las líneas rectas\(\text{AB}, \ \text{CD}, \ \text{AC}\) y\(\text{BD}\). Llamemos a estas Ecuaciones\(α = 0, \ β = 0, \ γ = 0\) y\(δ = 0\) respectivamente (figura\(\text{II.39}\)).

Entonces\(αβ = 0\) es la Ecuación que representa las dos líneas rectas\(\text{AB}\) y\(\text{CD}\), y\(γδ = 0\) es la Ecuación que representa las dos líneas rectas\(\text{AC}\) y\(\text{BD}\). La Ecuación\(αβ + λγδ = 0\), donde\(λ\) es una constante arbitraria, es una Ecuación de segundo grado que representa cualquier sección cónica que pase por los puntos\(\text{A}\),\(\text{B}\),\(\text{C}\) y\(\text{D}\). Al insertar las coordenadas de\(\text{E}\) en esta Ecuación, podemos encontrar el valor de\(λ\) que obliga a la Ecuación a pasar por los cinco puntos. Este modelo de falta de claridad quedará claro al seguir un cálculo real para los cinco puntos del presente ejemplo.

\(\text{FIGURE II.39}\)

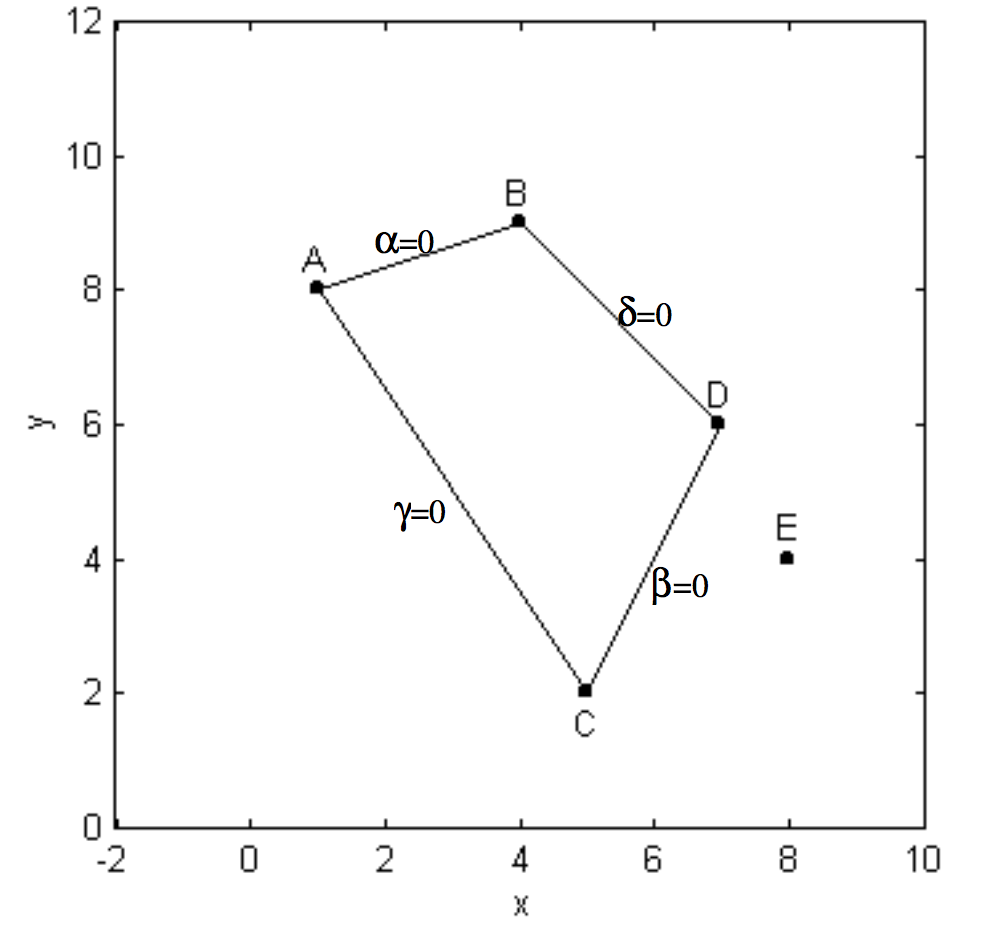
Las cuatro líneas rectas son

\(α=0: \quad x - 3y + 23 = 0\)

\(β=0: \quad 2x - y - 8 = 0\)

\(γ=0: \quad 3x + 2y - 19 = 0\)

\(δ=0: \quad x + y -13 = 0\)

Los dos pares de líneas son

\(αβ=0: \quad 2x^2 - 7xy + 3y^2 + 38x + y -184 = 0\)

\(γδ=0: \quad 3x^2 + 5xy + 2y^2 -58x -45y +247 =0\)

y la familia de secciones cónicas que atraviesa\(\text{A, B, C}\) y\(\text{D}\) es

\(αβ + λγδ = 0:\)

\((2+3λ)x^2 - (7-5λ)xy + (3+2λ)y^2 + (38-58λ)x + (1-45λ)y - 184 + 247λ = 0.\)

Ahora sustituya\(x = 8\),\(y = 4\) para obligar a la sección cónica a pasar por el punto\(\text{E}\). Esto da como resultado el valor

\(λ=\frac{76}{13}.\)

Por lo tanto, la ecuación a la sección cónica que pasa por los cinco puntos es

\(508x^2 + 578xy +382y^2 - 7828x - 6814y + 32760 = 0\)

Podemos, si se desea, dividir esta Ecuación por\(2\) (ya que todos los coeficientes son pares), o por\(32760\) (para hacer que el término constante sea igual a\(1\)) pero, para hacer más fácil el análisis que va a seguir, elijo dejar la Ecuación en la forma anterior, para que las constantes\(f\),\(g\) y \(h\)permanecen enteros.

Las constantes tienen los valores

\(a=508, b=382, c=32760, f=-3407, g=-3914, h=289\)

y los cofactores tienen los valores

\(\bar a = 906 \ 671, \quad \bar b = 1 \ 322 \ 684, \quad \bar c = 110 \ 535\)

\(\bar f = 599 \ 610, \quad \bar g = 510 \ 525, \quad \bar h = 3 \ 867 \ 358\)

Consultemos la tabla dicotómica. El valor del determinante es\(∆ = a\bar{a} + h\bar{h} + g\bar{g} (\text{or} \ h\bar{h} + b\bar{b} + f\bar{f}, \ \text{or} \ g\bar{g} + f\bar{f} + c\bar{c}\); pruebe las tres sumas para verificar si hay errores aritméticos). Se trata de\(∆ = −419 \ 939 \ 520\), así que procedemos a la opción\(5\). \(\bar{c} > 0\), por lo que procedemos a la opción\(6\). \(a\)y\(∆\) tienen signos opuestos, por lo que procedemos a\(7\). \(a\)no es igual\(b\), ni es\(h\) igual a cero. Por lo tanto tenemos una elipse. Se dibuja en figura\(\text{II.40}\).

\(\text{FIGURE II.40}\)

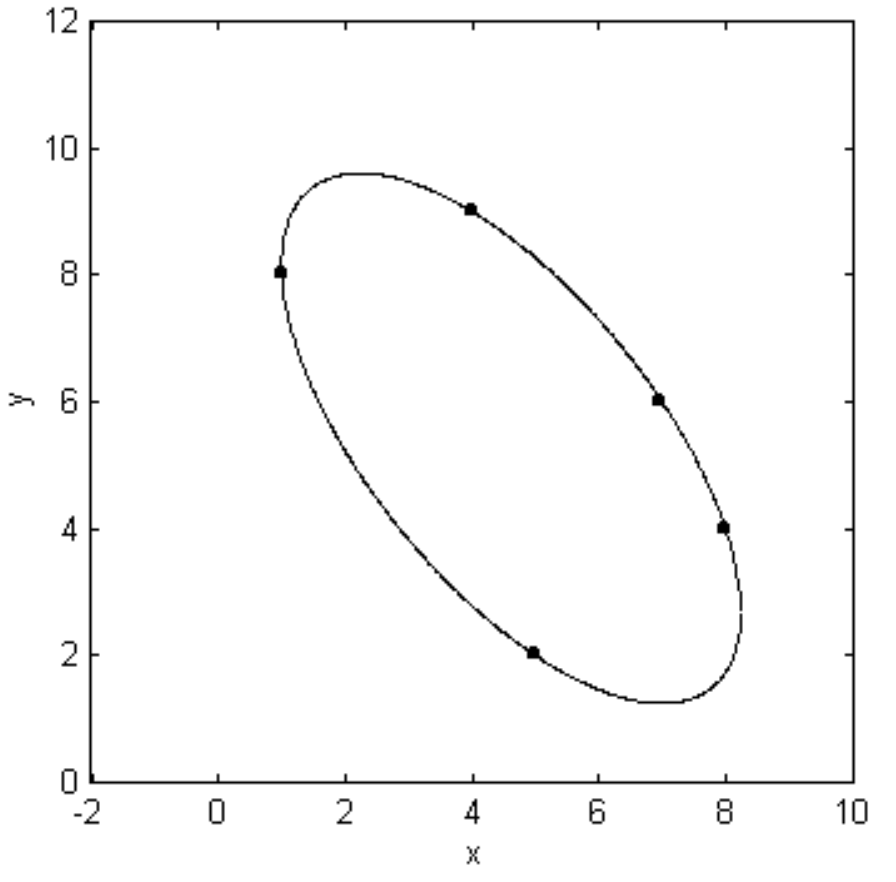
El centro de la elipse está en\((4.619, \ 5.425)\), y su eje mayor está inclinado en un ángulo\(128^\circ \ 51^\prime\) con respecto al\(x\) eje. Si ahora sustituimos\(x + 4.619\) por\(x\) y\(y + 5.425\) para\(y\), y luego\(x \cos 128^\circ 51^\prime + y \sin 128^\circ 51^\prime\) sustituimos el nuevo valor de\(x\) y\(−x \sin 128^\circ 51^\prime + y \cos 128^\circ 51^\prime\) por el nuevo valor de\(y\), la Ecuación asumirá su forma familiar para una elipse referida a sus ejes como ejes de coordenadas y su centro como origen.