2.6: La Sección Cónica General

La Ecuación\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \label{2.7.1} \tag{2.7.1}\]

representa una elipse cuyo eje mayor está a lo largo del\(x\) eje y cuyo centro está en el origen de las coordenadas. Pero, ¿y si su centro no está en el origen, y si el eje mayor está en algún ángulo sesgado con\(x\) respecto al eje? ¿Cuál será la Ecuación que represente tal elipse? Figura\(\text{II.37}\).

\(\text{FIGURE II.37}\)

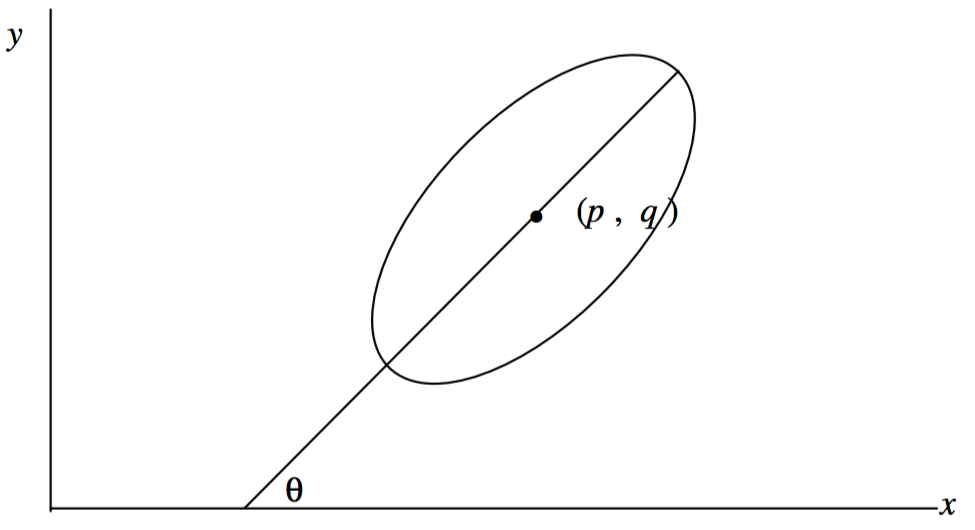
Si el centro se traduce del origen al punto\((p, q)\), la Ecuación que representa la elipse se encontrará reemplazando\(x\) por\(x − p\) y\(y\) por\(y − q\). Si el eje mayor está inclinado en un ángulo θ con\(x\) respecto al eje, la Ecuación que representa la elipse se encontrará reemplazando\(x\) por\(x \cos θ + y \sin θ\) y\(y\) por\(−x \sin θ + y \cos θ\). En cualquier caso, si la elipse se traduce o gira o ambos,\(x\) y cada uno\(y\) será reemplazado por expresiones lineales en\(x\) y\(y\), y la Ecuación resultante tendrá como máximo términos en\(x^2 , \ y^2 , \ xy, \ x, \ y\) y una constante. Lo mismo ocurre con una parábola o una hipérbola. Así, cualquiera de estas tres curvas estará representada por una Ecuación de la forma

\[ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0. \label{2.7.2} \tag{2.7.2}\]

(Los coeficientes\(a\) y no\(b\) son los ejes semi mayor y semi menor.) La notación aparentemente aleatoria para los coeficientes surge porque estas figuras son secciones planas de superficies tridimensionales (elipsoide, paraboloide e hiperboloide) las cuales son descritas por términos que involucran la coordenada así\(z\) como\(x\) y\(y\). La notación habitual para estas superficies tridimensionales es muy sistemática, pero cuando se\(z\) eliminan los términos en para el caso bidimensional, la notación aparentemente aleatoria\(a, \ b, \ c, \ f, \ g, \ h\) permanece. En cualquier caso, la Ecuación anterior se puede dividir por el término constante sin pérdida de generalidad, de manera que la Ecuación a una elipse, parábola o hipérbola se puede escribir, si se prefiere, como

\[ax^2 + 2hxy + by^2 + 2gx + 2fy + 1 = 0. \label{2.7.3} \tag{2.7.3}\]

¿Es cierto lo contrario? Es decir, ¿una Ecuación de esta forma siempre representa necesariamente una elipse, parábola o hipérbola?

No del todo. Por ejemplo,

\[6x^2 + xy - y^2 - 17x - y + 12 = 0 \label{2.7.4} \tag{2.7.4}\]

representa dos líneas rectas (se puede factorizar en dos términos lineales, pruébalo), mientras

\[2x^2 -4xy + 4y^2 -4x + 4 = 0 \label{2.7.5} \tag{2.7.5}\]

se satisface sólo por un solo punto. (Encuéntralo.)

No obstante, una sección plana de un cono puede ser de dos líneas o de un solo punto, así que quizás ahora podamos preguntarnos si la Ecuación general de segundo grado siempre debe representar una sección cónica. La respuesta es: cerca, pero no del todo.

Por ejemplo,

\[4x^2 + 12xy + 9y^2 + 14x + 21y + 6 = 0 \label{2.7.6} \tag{2.7.6}\]

representa dos líneas rectas paralelas, mientras

\[x^2 + y^2 + 3x + 4y + 15 = 0 \label{2.7.7} \tag{2.7.7}\]

no puede ser satisfecho por ningún real\((x,y)\).

Sin embargo, un plano puede intersectar un cilindro en dos líneas rectas paralelas, o una sola línea recta, o no en absoluto. Por lo tanto, si estiramos un poco la definición de un cono para incluir un cilindro como caso limitante especial, entonces podemos decir que la Ecuación general de segundo grado\(y\) en\(x\) y de hecho siempre representa una sección cónica.

¿Hay algún medio por el cual se pueda decir de un vistazo a una ecuación de segundo grado en particular, por ejemplo

\[8x^2 + 10xy -3y^2 -2x - 4y - 2 = 0, \label{2.7.8} \tag{2.7.8}\]

¿qué tipo de sección cónica se representa? La respuesta es sí, y esta pasa a ser una hipérbola. La discriminación se realiza mediante el examen de las propiedades del determinante

\ begin {array} {l | c c c |}
& a & h & g\
\ Delta = & h & b & f\\
& g & f & c\
\ etiqueta {2.7.9}\ tag {2.7.9}
\ end {array}

He ideado una tabla después del diseño de las tablas dicotómicas comúnmente utilizadas por los taxonomistas en biología, en la que el usuario se enfrenta a un pareado (o a veces triplete) de alternativas, y luego se dirige a la siguiente parte de la tabla. Le perdonaré al lector la derivación de la tabla; en cambio, describiré su uso.

En la tabla, he usado el símbolo\(\bar{a}\) para significar el cofactor de\(a\) en el determinante,\(\bar{h}\) el cofactor de\(h\),\(\bar{g}\) el cofactor de\(g\), etc. explícitamente, estos son

\[\bar{a} = bc - f^2 , \label{2.7.10} \tag{2.7.10}\]
\[\bar{b} = ca - g^2 , \label{2.7.11} \tag{2.7.11}\]
\[\bar{c} = ab - h^2 , \label{2.7.12} \tag{2.7.12}\]
\[\bar{f} = gh - af , \label{2.7.13} \tag{2.7.13}\]
\[\bar{g} = hf - bg \label{2.7.14} \tag{2.7.14}\]
y\[\bar{h} = fg - ch . \label{2.7.15} \tag{2.7.15}\]

La primera columna etiqueta las elecciones que se le pide al usuario que haga. Al principio, hay dos opciones que hacer,\(1\) y\(1^\prime\) La segunda columna dice cuáles son estas elecciones, y la cuarta columna dice a dónde ir a continuación. Así, si el determinante es cero, vaya a\(2\); de lo contrario, vaya a\(5\). Si hay un asterisco en la columna\(4\), ya está terminado. Columna\(3\) dice a qué tipo de sección cónica has llegado, y columna\(5\) da un ejemplo.

No importa de qué tipo sea la sección cónica, las coordenadas de su centro son\((\bar{g}/\bar{c}, \ \bar{f}/\bar{c} )\) y el ángulo\(θ\) que su eje mayor o transversal hace con el eje x viene dado por

\[\tan 2θ = \frac{2h}{a-b}. \label{2.7.16} \tag{2.7.16}\]

Así, si primero\(x\) se reemplaza por\(x + \bar{g} / \bar{c}\) y\(y\) con\(y + \bar{f}/\bar{c}\), y luego\(x\) se reemplaza el nuevo por\(x \cos θ − y \sin θ\) y el nuevo\(y\) con\(x \sin θ + y \cos θ\), la Ecuación tomará la forma familiar de una sección cónica con su eje mayor o transversal coincidente con el\(x\) eje y su centro en el origen. Cualquiera de sus propiedades, como la excentricidad, se puede deducir entonces de las ecuaciones familiares. Deberías probar esto con Ecuación\(\ref{2.7.8}\).

Clave de las Secciones Cónicas

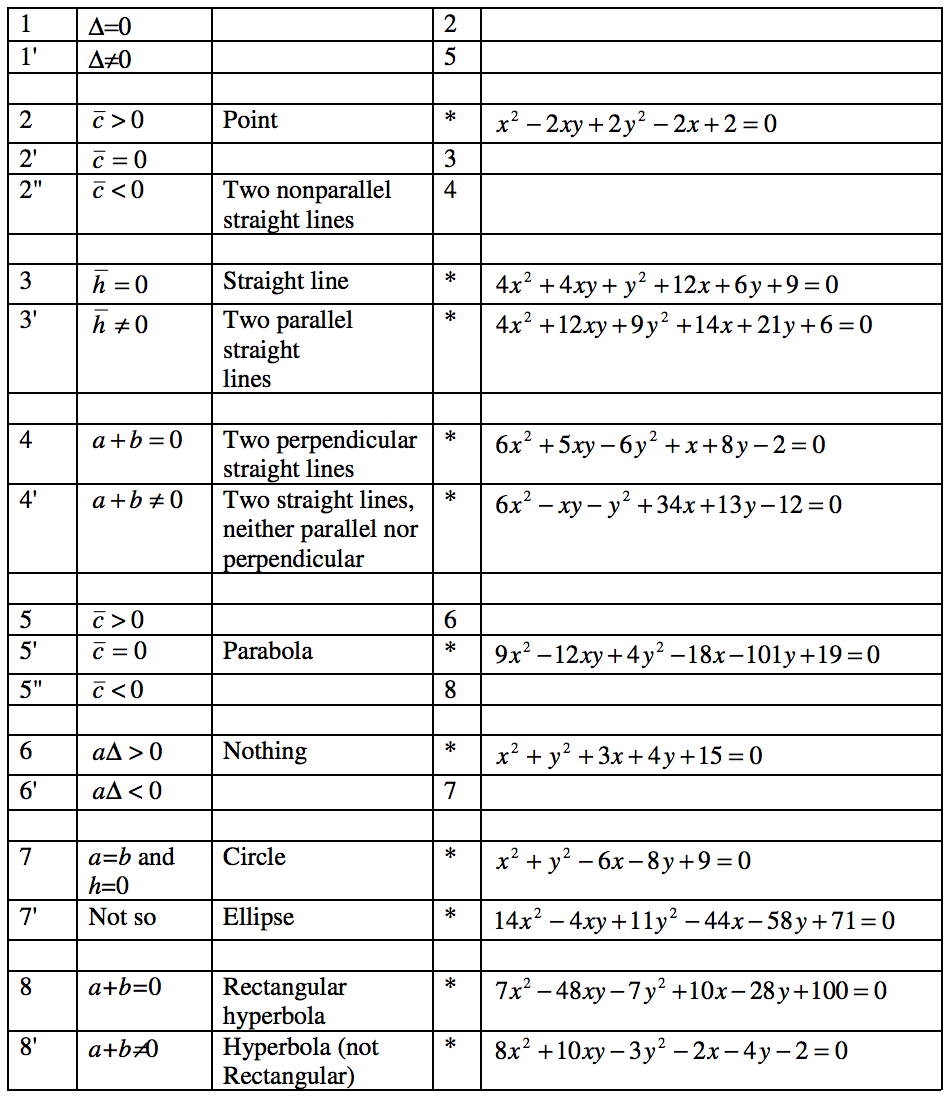
Ante una Ecuación general de segundo grado en\(x\) y\(y\), a menudo me parece conveniente desde el principio calcular los valores de los cofactores a partir de las Ecuaciones 2.7.10 − 2.7.15.

Aquí hay un ejercicio que tal vez te gustaría probar. Mostrar que la elipse\(ax^2 + 2hxy + by^2 + 2gx + 2fy + 1 = 0\) está contenida dentro del rectángulo cuyos lados están

\[x = \frac{\bar{g} \pm \sqrt{\bar{g}^2 - \bar{a} \bar{c}}}{\bar{c}} \label{2.7.18} \tag{2.7.18}\]

\[y = \frac{\bar{f} \pm \sqrt{\bar{f}^2 - \bar{b} \bar{c}}}{\bar{c}} \label{2.7.19} \tag{2.7.19}\]

En otras palabras, estas cuatro líneas son las tangentes vertical y horizontal a la elipse.

Esto probablemente no sea de mucha utilidad en la mecánica celeste, pero probablemente será útil para estudiar elipses Lissajous, o los parámetros Stokes de la luz polarizada. También es útil en la programación de una computadora para dibujar, por ejemplo, la elipse\(14x^2 - 4xy + 11y^2 - 44x -58y + 71 = 0\). Para ello, probablemente querrás comenzar en algún valor de\(x\) y calcular los dos valores correspondientes de\(y\), y luego pasar a otro valor de\(x\). Pero ¿a qué valor de\(x\) deberías empezar? La ecuación\(\ref{2.7.18}\) te lo dirá.

Pero, ¿qué\(\ref{2.7.19}\) significan las Ecuaciones\(\ref{2.7.18}\) y si la sección cónica Ecuación no\(ax^2 + 2hxy + by^2 + 2gx + 2fy + 1 = 0\) es una elipse? Siguen siendo útiles si la sección cónica es una hipérbola. Las ecuaciones\(\ref{2.7.18}\) y\(\ref{2.7.19}\) siguen siendo tangentes verticales y horizontales -pero en este caso la hipérbola queda totalmente fuera de los límites impuestos por estas tangentes. Si los ejes de la hipérbola son horizontales y verticales, uno u otro de Ecuaciones\(\ref{2.7.18}\) y\(\ref{2.7.19}\) fallará.

Si la sección cónica es una parábola, las ecuaciones\(\ref{2.7.18}\) y no\(\ref{2.7.19}\) son útiles, porque\(c = 0\). Sólo hay una tangente horizontal y sólo una tangente vertical. Ellos son dados por

\[x = \frac{\bar{a}}{2\bar{g}} \label{2.7.20} \tag{2.7.20}\]

y\[y = \frac{\bar{b}}{2\bar{f}} \tag{2.7.21} \label{2.7.21}\]

Si el eje de la parábola es horizontal o vertical, uno u otro de Ecuaciones\(\ref{2.7.20}\) y\(\ref{2.7.21}\) fallará.

Si la Ecuación de segundo grado representa una o dos líneas rectas, o un punto, o nada, me imagino que todas las Ecuaciones\(\ref{2.7.18}\) −\(\ref{2.7.21}\) fallarán, a menos que tal vez la Ecuación represente líneas horizontales o verticales. No he investigado esto; tal vez al lector le gustaría hacerlo.

Aquí hay un problema que tal vez te gustaría probar. La Ecuación\(8x^2 + 10xy - 3y^2 - 2x - 4y - 2 = 0\) representa una hipérbola. ¿Cuáles son las Ecuaciones a sus ejes, a sus asíntotas y a su hipérbola conjugada? O, más generalmente, si\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0\) representa una hipérbola, ¿cuáles son las Ecuaciones a sus ejes, a sus asíntotas y a su hipérbola conjugada?

Antes de comenzar, un punto digno de mención es que la hipérbola original, sus asíntotas, y la hipérbola conjugada) tienen el mismo centro, lo que significa que\(g\) y\(f\) son iguales para cada uno, y tienen los mismos ejes, lo que significa que\(a\)\(h\),, y\(b\) son los mismos para cada uno. Se diferencian sólo en el término constante.

Si haces el primer problema,\(8x^2 + 10xy - 3y^2 - 2x - 4y -2 = 0\), habrá una buena cantidad de trabajo numérico por hacer. Cuando lo hice no usé lápiz y papel ni calculadora de mano. Más bien me senté frente a una computadora haciendo los cálculos numéricos con una declaración Fortran para cada etapa del cálculo. No creo que pudiera haberlo hecho de otra manera sin cometer muchos errores. Lo primero que hice fue resolver los cofactores\(\bar{a}, \ \bar{h}, \ \bar{b}, \ \bar{g}, \ \bar{f}, \ \bar{c}\) y almacenarlos en la computadora, y también las coordenadas del centro\((x_0, y_0)\) de la hipérbola, que están dadas por\(x_0 = \bar{g}/\bar{c}, \ y_0 = \bar{f} / \bar{c}\).

Ya sea que haga el problema numérico particular, o el algebraico más general, le sugiero que proceda de la siguiente manera. Primero, remitir la hipérbola a un conjunto de coordenadas\(x^\prime , y^\prime\) cuyo origen coincide con los ejes de la hipérbola. Esto se hace reemplazando\(x\) con\(x^\prime + x_0\) y\(y\) con\(y' + y_0\). Esto dará como resultado una Ecuación de la forma\(ax^{\prime 2} + 2hx^\prime y^\prime + by^{\prime 2} + c^\prime = 0\). Los coeficientes de los términos cuadráticos permanecerán inalterados, los términos lineales habrán desaparecido y el término constante habrá cambiado. En esta etapa obtuve, para el ejemplo numérico,\(8x^{\prime 2} + 10x^\prime y^\prime - 3y^{\prime 2} - 1.8163 = 0\).

Ahora refiera la hipérbola a un conjunto de coordenadas\(x^{\prime \prime}, y^{\prime \prime}\) cuyos ejes son paralelos a los ejes de la hipérbola. Esto se logra reemplazando\(x^\prime\) con\(x^{\prime \prime} \cos θ − y^{\prime \prime} \sin θ\) y\(y^\prime\) con\(x^{\prime \prime} \sin θ + y^{\prime \prime} \cos θ\), donde\(\tan 2θ = 2h /(a − b)\). Aquí va a haber un pequeño problema, porque esto da dos valores de\(θ\) diferir por\(90^\circ\), y querrás decidir cuál quieres. En cualquier caso, el resultado será una Ecuación de la forma\(a^{\prime \prime} x^{\prime \prime 2} + b^{\prime \prime} y^{\prime \prime 2} + c^\prime = 0\), en la que\(a^{\prime \prime}\) y\(b^{\prime \prime}\) son de signo opuesto. Además, si llegas a entender el significado del ruido “La traza de una matriz es invariante bajo una transformación ortogonal”, podrás comprobar si hay errores aritméticos al anotarlo\(a^{\prime \prime} + b^{\prime \prime} = a + b\). Si esto no es así, has cometido un error. Además, el término constante debe ser inalterado por la rotación (tenga en cuenta el primo único en el\(c\)). En esta etapa, obtuve\( 9.933 x^{\prime \prime 2} - 4.933y^{\prime \prime 2} - 1.8163 = 0\). (Todo esto se hizo con declaraciones Fortran en la computadora -ningún cálculo real o escritura hecha por mí- y los números se almacenaron en la computadora a muchas cifras significativas).

En cualquier caso esta Ecuación se puede escribir en la forma familiar\(\dfrac{x^{\prime \prime 2}}{A^2}-\dfrac{y^{\prime \prime 2}}{B^2}=1\), que en este caso hice para ser\(\dfrac{x^{\prime \prime 2}}{0.4283^2}-\dfrac{y^{\prime \prime 2}}{0.6088^2}=1\). Ahora estamos en terreno familiar. Los ejes de la hipérbola son\( x^{\prime \prime} = 0\) y\(y^{\prime \prime} = 0\), las asíntotas son\(\dfrac{x^{\prime \prime 2}}{A^2} - \dfrac{y^{\prime \prime 2}}{B^2} = 0\) y la hipérbola conjugada es\(\dfrac{x^{\prime \prime 2}}{A^2} - \dfrac{y^{\prime \prime 2}}{B^2} = -1\).

Ahora, partiendo de\(\dfrac{x^{\prime \prime 2}}{A^2} - \dfrac{y^{\prime \prime 2}}{B^2} = -1\) para las asíntotas, o de\(\dfrac{x^{\prime \prime 2}}{A^2} - \dfrac{y^{\prime \prime 2}}{B^2} =-1\) para la hipérbola conjugada, invertimos el proceso. Vamos a las coordenadas de un solo cebado reemplazando\(x^{\prime \prime}\) con\(x^\prime \cos θ + y^\prime \sin θ\) y\(y^{\prime \prime}\) con −\(x^\prime \sin θ + y' \cos θ\), y luego a las coordenadas originales reemplazando\(x^\prime\) con\(x − x_0\) y\(y^\prime\) con\(y − y_0\).

Esto es lo que encuentro:

Hipérbola original:\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0\)

Hipérbola conjugada:\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c_{\text{conj}} = 0,\)
donde\(c_{\text{conj}} = -(2g \bar{g} + 2f \bar{f} + c \bar{c})/ \bar{c} = -(2gx_0 + 2fy_0 + c).\)

Asintotas:\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c_{\text{asymp}} = 0,\)
donde se\(c_{\text{asymp}}\) puede escribir en cualquiera de las siguientes formas equivalentes:
\[c_{\text{asymp}} = + (a \bar{g}^2 + 2h \bar{g} \bar{f} + b \bar{f}^2 ) / \bar{c}^2 = ax_0^2 + 2hx_0 y_0 + by_0^2 = -(g \bar{g} + f \bar{f}) / \bar{c} .\]
[La última de estas tres formas se puede derivar muy rápidamente recordando que una condición para una ecuación general de segundo grado en\(x\) y\(y\) para representar dos líneas rectas es que el determinante\(∆\) debe ser cero. Una mirada a este determinante demostrará que esto implica que\(g\bar{g} + f\bar{f} + c\bar{c} = 0.\)]

Ejes de hipérbolas:\((y - x \tan θ - y_0 + x_0 \tan θ) ( y + x \cot θ - y_0 - x_0 \cot θ) = 0,\)
donde\( \tan 2 θ = 2h / (a-b) . \)

Ejemplo:

Hipérbola original:\(8x^2 + 10xy - 3y^2 - 2x - 4y - 2 = 0\)

Hipérbola conjugada:\(8x^2 + 10xy - 3y^2 - 2x - 4y + \frac{80}{49} = 0\)

Asíntotas:\(8x^2 + 10xy - 3y^2 - 2x -4y - \frac{9}{49} = 0 , \)
que también se pueden escribir\((4x - y - \frac{9}{7})(2x + 3y + \frac{1}{7}) = 0\)

Ejes de hipérbolas:\(( y − 0.3866x + 0.3275)( y + 2.5866 x − 0.4613)\).

Estos se muestran en la siguiente figura: la hipérbola original en negro, el conjugado en azul.

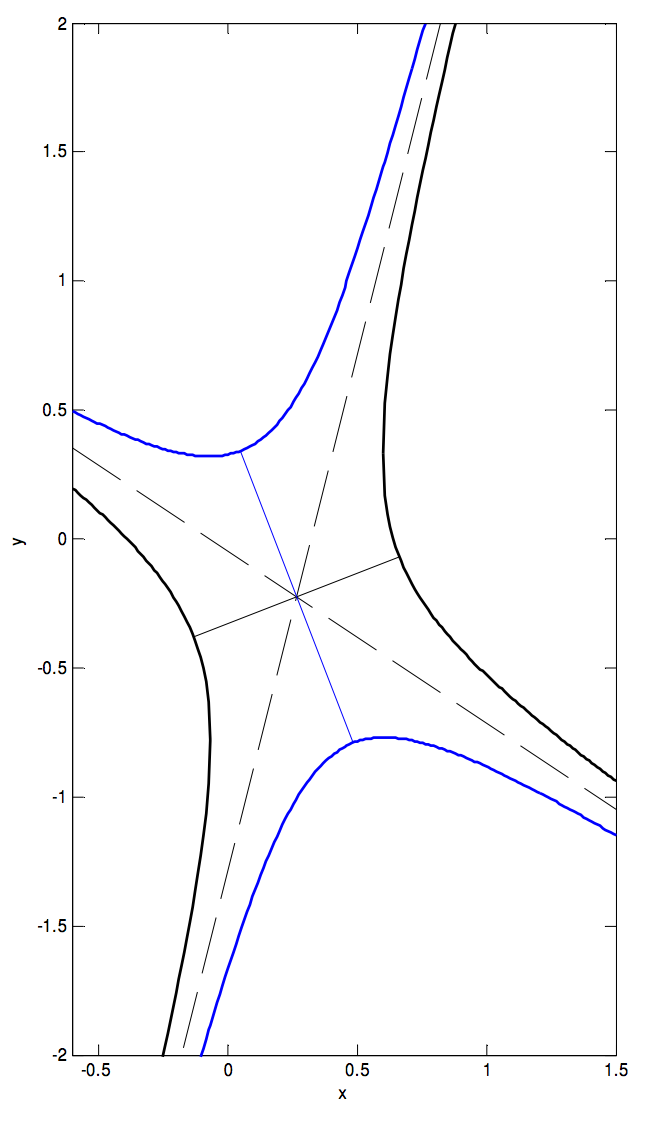
El centro está en (0.26531, −0.22449).

Las laderas de las dos asíntotas son 4 y\(−\frac{2}{3}\). De la Ecuación 2.2.16 encontramos que la tangente del ángulo entre las asíntotas es\(\tan 2ψ = \frac{14}{5}\), de manera que\(2ψ = 70^\circ .3\), y el ángulo entre la asíntota y el eje mayor de la hipérbola original es\(54^\circ .8\), o\(\tan ψ = 1.419\). Esto es igual (ver Ecuaciones 2.5.3 y 2.5.10) a\(\sqrt{e^2 - 1}\), por lo que la excentricidad de la hipérbola original es\(1.735\). De la Sección 2.2, en breve Ecuación 2,5,6, pronto encontramos que la excentricidad de la hipérbola conjugada es\(\csc ψ = 1.223\).

A mí se me ocurre una pregunta interesante. Hemos encontrado que, si\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0\) es una hipérbola, entonces las Ecuaciones a la hipérbola conjugada y las asíntotas son de una forma similar, es decir\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c_{\text{conj}} = 0\) y\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c_{\text{asymp}} = 0\), y encontramos expresiones para\(c_{\text{conj}}\) y\(c_\text{asymp}\). Pero, ¿y si no\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0\) es una hipérbola? ¿Y si es una elipse? ¿Qué representan las otras Ecuaciones, dado que una elipse no tiene ni conjugado ni asíntotas?

Por ejemplo,\(14x^2 - 4xy + 11y^2 - 44x -58y + 71 = 0\) es una elipse. ¿Qué son\(14x^2 - 4xy + 11y^2 - 44x - 58y + 191 = 0\) y\(14x^2 -4xy + 11y^2 - 44x - 58y + 131 = 0\)? Yo usé la clave en la página 47, y me decía que la primera de estas Ecuaciones no está satisfecha por ningún punto real, lo que supongo es la forma de la Ecuación de decirme que no existe tal cosa como el conjugado a una elipse. Se suponía que la segunda Ecuación serían las “asíntotas”, pero la clave me muestra que la Ecuación se satisface con un solo punto real, a saber (2, 3), que coincide con el centro de la elipse original. Eso no me lo esperaba. ¿Debería haberlo hecho?