3.2: Triángulos Planos

Esta sección es para servir como un breve recordatorio de cómo resolver un triángulo plano. Si bien puede haber una tentación de pasar rápidamente sobre esta sección, sí contiene una advertencia que se volverá aún más pertinente en la sección sobre triángulos esféricos.

Convencionalmente, un triángulo plano se describe por sus tres ángulos\(A\)\(B\),,\(C\) y tres lados\(a\)\(b\),\(c\), con un ser opuesto a\(A\),\(b\) opuesto a\(B\), y\(c\) opuesto a\(C\). Ver figura\(\text{III.1}\).

\(\text{FIGURE III.1}\)

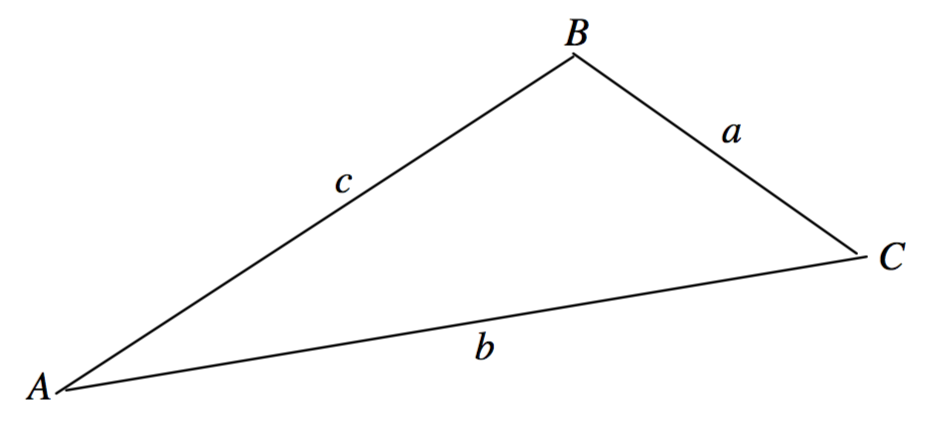
Se supone que el lector está familiarizado con las fórmulas seno y coseno para la solución del triángulo:

\[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} \label{3.2.1} \tag{3.2.1}\]

y\[a^2 = b^2 + c^2 - 2bc \cos A , \label{3.2.2} \tag{3.2.2}\]

y entiende que el arte de resolver un triángulo implica el reconocimiento de qué fórmula es apropiada bajo qué circunstancias. Dos ejemplos rápidos, cada uno con una advertencia, bastarán.

Ejemplo: Un triángulo plano tiene lados\(a = 7\) pulgadas,\(b = 4\) pulgadas y ángulo\(B = 28^\circ\). Encuentra el ángulo\(A\).

\(\text{FIGURE III.2}\)

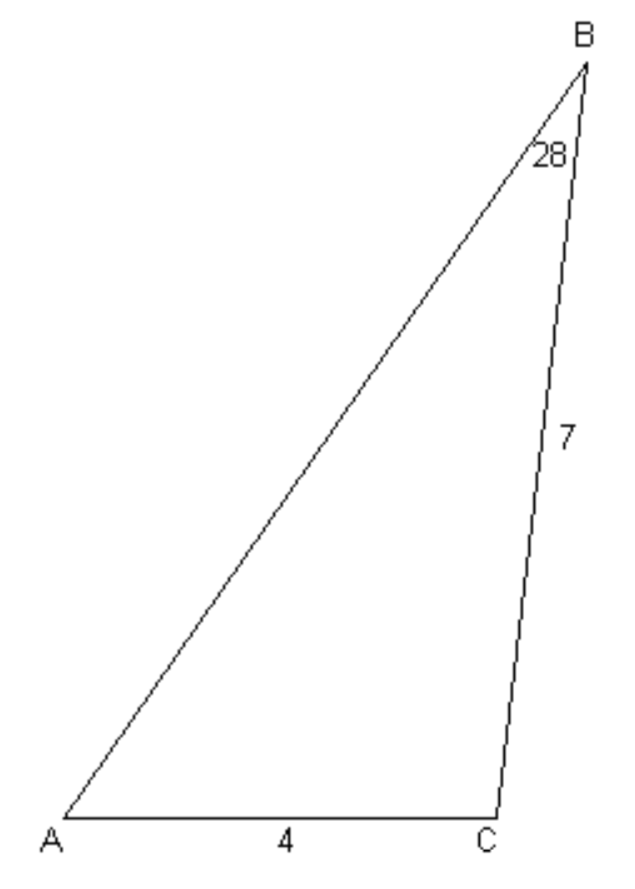
Ver figura\(\text{III.2}\)

Utilizamos la fórmula sinusoidal, para obtener

\(\sin A = \frac{7 \sin 28^\circ}{4} = 0.821575\)

\(A = 55^\circ 14^\prime .6\)

El escollo es que hay dos valores de\(A\) entre\(0^\circ\) y\(180^\circ\) que satisfacen\(\sin A = 0.821575\), a saber\(55^\circ \ 14^\prime.6\) y\(124^\circ \ 45^\prime.4\). La figura\(\text{III.3}\) muestra que, dados los datos originales, cualquiera de estos es una solución válida.

\(\text{FIGURE III.3}\)

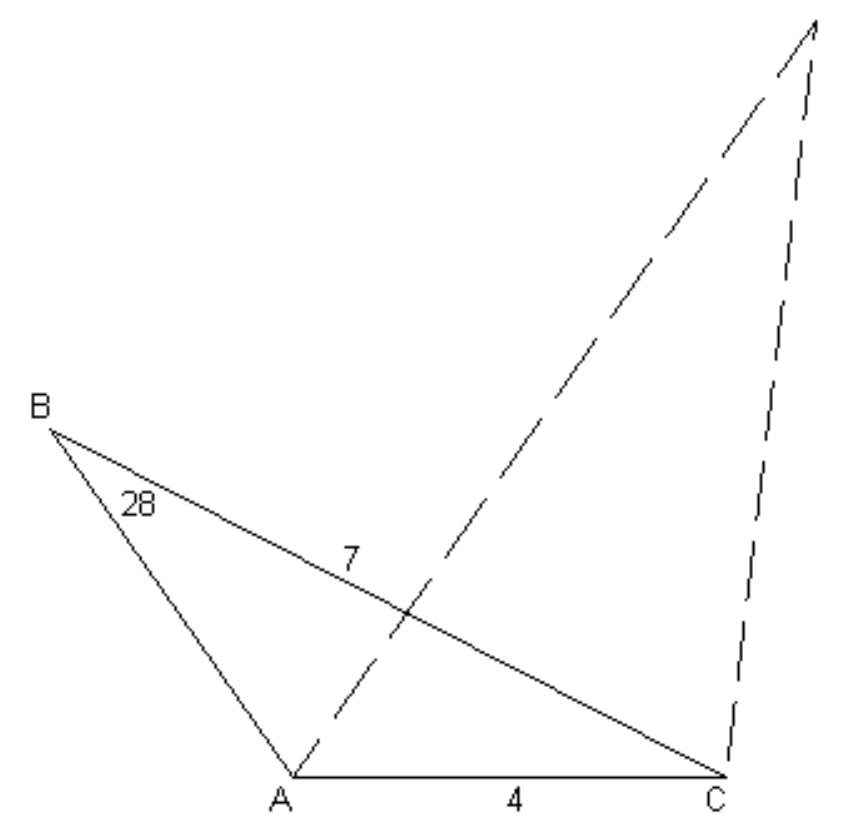
La lección que hay que aprender de esto es que todas las funciones trigonométricas inversas\((\sin^{-1} , \cos^{-1} , \tan^{-1} )\) tienen dos soluciones entre\(0^\circ\) y\(360^\circ\). La función\(\sin^{-1}\) es particularmente problemática ya que, para argumentos positivos, tiene dos soluciones entre\(0^\circ\) y\(180^\circ\). El lector siempre debe estar en guardia ante los “problemas de cuadrante” (es decir, determinar a qué cuadrante pertenece la solución deseada) y se le advierte que, a menos que se tenga especial cuidado en la programación de calculadoras o computadoras, los problemas de cuadrante se encuentran entre los problemas más frecuentes en la trigonometría, y especialmente en astronomía esférica.

Ejemplo: Encuentra\(x\) en el triángulo ilustrado en la figura\(\text{III.4}\).

\(\text{FIGURE III.4}\)

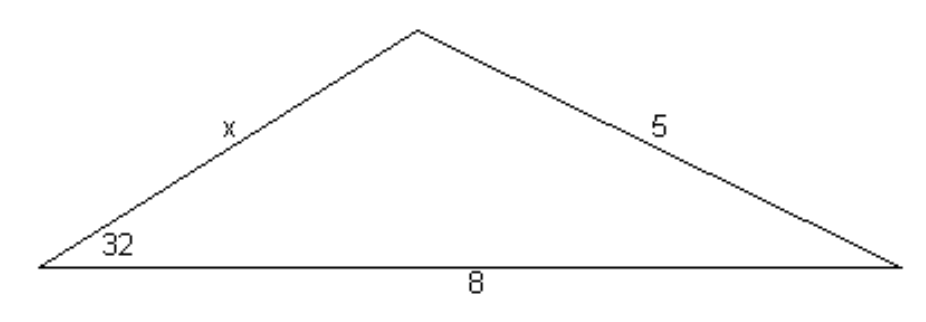
La aplicación de la regla coseno da como resultado

\(25 = x^2 + 64 - 16x \cos 32^\circ\)

Solución de los rendimientos de la ecuación cuadrática

\(x = 4.133 \ \text{or} \ 9.435\)

Esto ilustra que el problema de las “dos soluciones” no se limita solo a los ángulos. La figura\(\text{III.4}\) se dibuja a escala para una de las soluciones; el lector debe dibujar la segunda solución para ver cómo es que dos soluciones son posibles.

Ahora se invita al lector a probar los siguientes problemas “garantizados todos los diferentes” con calculadora manual. Algunos pueden tener dos soluciones reales. Algunos pueden no tener ninguno. El lector debe dibujar los triángulos con precisión, especialmente aquellos que tienen dos soluciones o ninguna solución. Es importante desarrollar una comprensión geométrica clara de los problemas trigonométricos, y no simplemente confiar en los cálculos automáticos de una máquina. El desarrollo de estas habilidades críticas ahora pagará dividendos en los problemas reales más complejos que se encuentran en la mecánica celeste y la computación orbital.

\(\text{PROBLEMS}\)

1. \(a = 6\ \ b = 4\ \ c = 7 \ C = ?\)

2. \(a= 5\ \ b = 3\ \ C = 43^\circ \ c = ?\)

3. \(a = 7\ \ b=9\ \ C = 110^\circ \ B=?\)

4. \( a = 4\ \ b=5\ \ A=29^\circ \ c = ? \)

5. \(a = 5\ \ b = 7\ \ A = 37^\circ \ B = ?\)

6. \(a = 8\ \ b=5\ \ A=54^\circ \ C=?\)

7. \(A=64^\circ \ B = 37^\circ \ a/c = ? \ b/c = ?\)

8. \(a = 3\ \ b = 8\ \ c = 4 \ C = ? \)

9. \(a = 4\ \ b=11\ \ A = 26^\circ \ c = ? \)

Ahora se invita además al lector a escribir un programa de computadora (en el idioma que sea más familiar) para resolver cada uno de los problemas anteriores para valores arbitrarios de los datos. Las longitudes deben leerse en entrada e imprimirse en salida a cuatro cifras significativas. Los ángulos deben ser leídos en entrada e impresos en salida en grados, minutos y décimas de minuto (e.g.\(47^\circ \ 12^\prime.9\)). La salida debe mostrar dos soluciones si hay dos, y debe imprimir “NO Solution” si no hay ninguna. Este ejercicio familiarizará al lector con la manipulación de ángulos, especialmente funciones trigonométricas inversas en cualquier lenguaje informático que se utilice, y será recompensado en futuras aplicaciones más avanzadas.

Soluciones a problemas.

1. \(C = 86^\circ 25^\prime.0\)
2. \(c=3.473\)
3. \(B=40^\circ 00^\prime.1\)
4. \(c=7.555 \text{ or } 1.191\)
5. \(B=57^\circ 24^\prime .6 \text{ or } 122^\circ 35^\prime .4\)
6. \(C=95^\circ 37^\prime .6 \text{ or } 23^\circ 37^\prime .6\)
7. \(a/c = 0.9165 \ b/c = 0.6131\)
8. No hay solución real
9. No hay solución real

El área de un triángulo plano es\(\frac{1}{2} × \text{base} × \text{height}\), y es fácil ver a partir de esto que

\[\text{Area} = \frac{1}{2} bc \sin A = \frac{1}{2} ca \sin B = \frac{1}{2} ab \sin C \label{3.2.3} \tag{3.2.3}\]

Al hacer uso\(\sin^2 A = 1 - \cos^2 A\) y\(\cos A = \left( b^2 + c^2 - a^2 \right)/(2bc)\), podemos expresarlo completamente en términos de las longitudes de los lados:

\[\text{Area} = \sqrt{s(s-a)(s-b)(s-c),} \label{3.2.4} \tag{3.2.4}\]

donde\(s\) está el semiperímetro\(\frac{1}{2}(a+b+c)\).