3.3: Coordenadas cilíndricas y esféricas

Se supone que el lector está al menos algo familiarizado con las coordenadas cilíndricas\((ρ, \phi, z)\) y las coordenadas esféricas\((r, θ, \phi)\) en tres dimensiones, y ofrezco aquí solo un breve resumen. La figura\(\text{III.5}\) ilustra las siguientes relaciones entre ellos y las coordenadas rectangulares\((x, y, z)\).

\[\begin{align} x &= ρ \cos \phi = r \sin θ \cos \phi \label{3.3.1} \\[8pt] y &= ρ \sin \phi = r \sin θ \sin \phi \label{3.3.2} \\[8pt] z &= r \cos θ \label{3.3.3} \end{align}\]

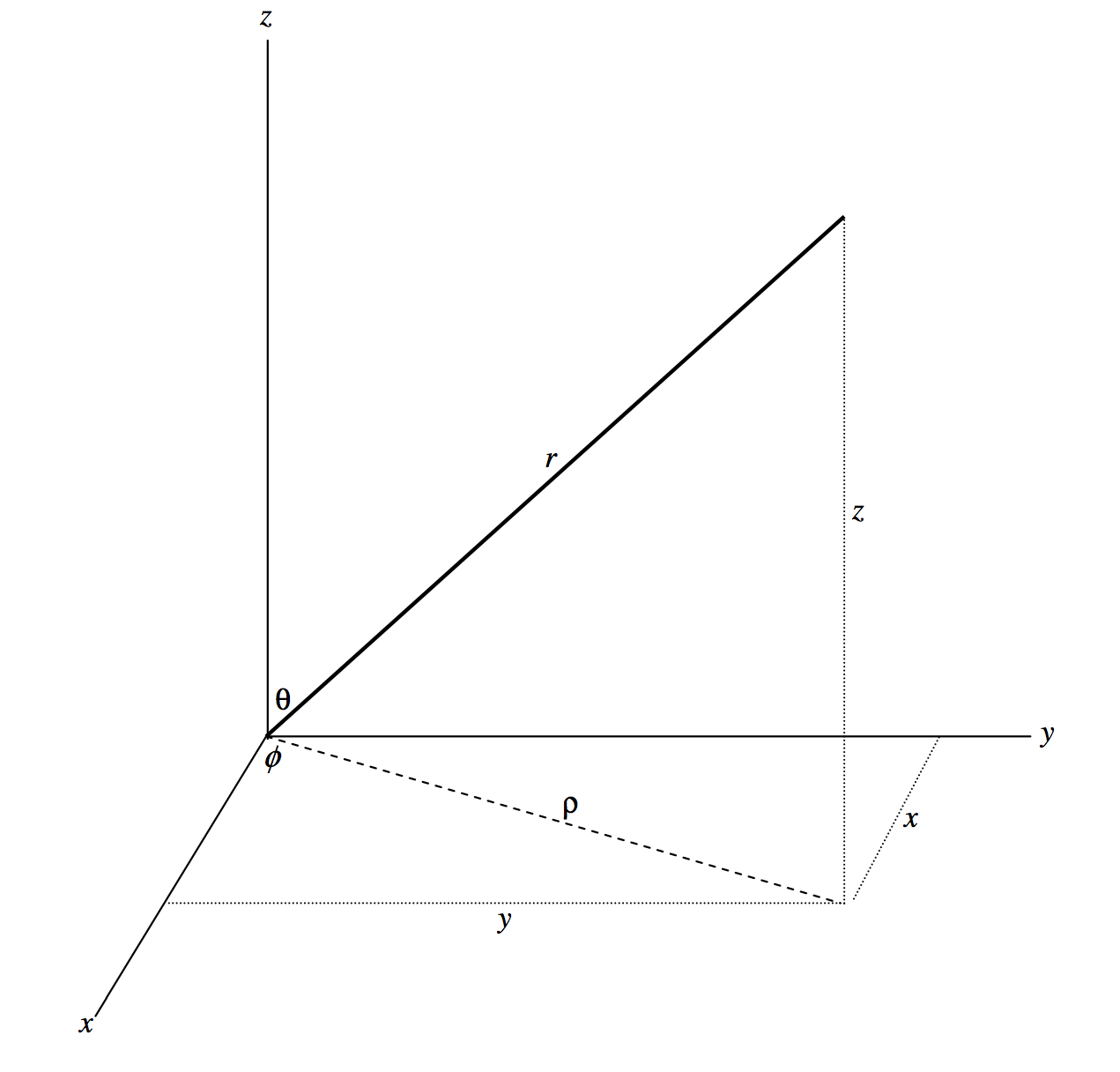
\(\text{FIGURE III.5}\)

Las relaciones inversas entre las coordenadas esféricas y rectangulares son

\[r = \sqrt{x^2 + y^2 + z^2} \label{3.3.4} \tag{3.3.4}\]

\[θ = \cos^{-1} \frac{z}{\sqrt{x^2 + y^2 + z^2}} \tag{3.3.5} \label{3.3.5}\]

\[\phi = \cos^{-1} \frac{x}{\sqrt{x^2 + y^2}} = \sin^{-1} \frac{y}{\sqrt{x^2 + y^2}} \label{3.3.6} \tag{3.3.6}\]

Las coordenadas\(r\),\(θ\) y\(\phi\) se denominan, respectivamente, las coordenadas “radial”, “polar” o “meridional”, y “azimutal” respectivamente.

Tenga en cuenta que\(r\) es esencialmente positivo (el símbolo √ denota el valor positivo o absoluto de la raíz cuadrada). El ángulo\(θ\) es necesariamente entre\(0^\circ\) y\(180^\circ\) y por lo tanto no hay ambigüedad cuadrante en la evaluación de\(θ\). El ángulo\(\phi\), sin embargo, puede estar entre\(0^\circ\) y\(360^\circ\). Por lo tanto, para determinar de\(\phi\) manera única,\(\phi\) deben evaluarse ambas fórmulas anteriores para, o los signos de\(x\) y\(y\) deben ser inspeccionados. No basta con calcular a\(\phi\) partir de\(\phi = \tan^{-1} (y/x)\) solo. El lector, sin embargo, debe ser consciente de que algunos lenguajes informáticos y algunas funciones de calculadora manual inspeccionarán los signos de\(x\) y\(y\) para usted y regresarán\(\phi\) en su cuadrante correcto. Por ejemplo, en\(\text{FORTRAN}\), la función\(\text{ATAN2(X,Y)}\) (o\(\text{DATAN2(X,Y)}\) en doble precisión) regresará de\(\phi\) manera única en su cuadrante correcto (aunque tal vez como un ángulo negativo, en cuyo caso\(360^\circ\) debería agregarse al ángulo de salida) siempre que los argumentos\(\text{X}\) y\(\text{Y}\) sean ingresados con sus signos correctos. Esto puede ahorrar una inmensa cantidad de problemas en la programación, y el lector debería familiarizarse con esta función.

Dirección Cosines

La dirección a un punto en el espacio tridimensional relativo al origen se puede describir, como hemos visto, por los dos ángulos\(θ\) y\(\phi\). Otra forma de describir la dirección a un punto, o la orientación de un vector, es dar los ángulos\(α, \ β, \ γ\) que el vector hace con los\(z\) ejes\(x\)\(y\) -, - y -respectivamente (ver figura\(\text{III.5}\)). El ángulo\(γ\) es el mismo que el ángulo\(θ\).

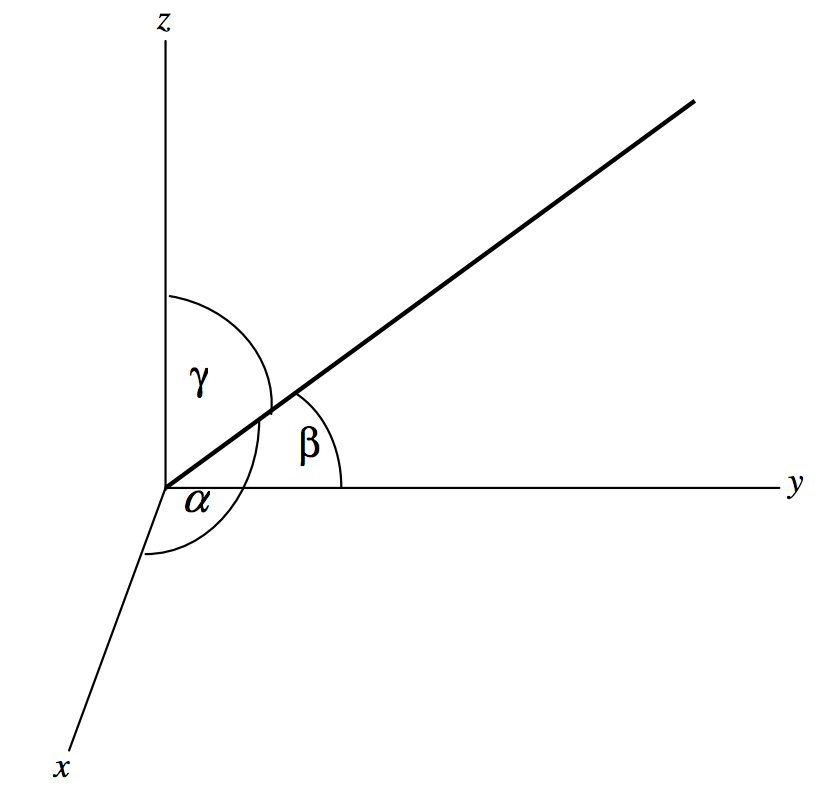
\(\text{FIGURE III.6}\)

Más comúnmente uno cita los cosenos de estos tres ángulos. Estos se llaman los cosenos de dirección, y a menudo se denotan por\((l,m,n)\). No debería pasar mucho tiempo para que el lector se convenza de que la relación entre los cosenos de dirección y los ángulos\(θ\) y\(\phi\) son

\[l = \cos α = \sin θ \cos \phi \label{3.3.7} \tag{3.3.7}\]

\[m = \cos β = \sin θ \sin \phi \label{3.3.8} \tag{3.3.8}\]

\[n = \cos γ = \cos θ \label{3.3.9} \tag{3.3.9}\]

Estos no son independientes, y están relacionados por

\[l^2 + m^2 + n^2 = 1. \label{3.3.10} \tag{3.3.10}\]

Un conjunto de números que son múltiplos de los cosenos de dirección -es decir, son proporcionales a ellos- se denominan relaciones de dirección.

Latitud y Longitud

La figura de la Tierra no es perfectamente esférica, pues está ligeramente aplanada en los polos. Por el momento, sin embargo, nuestro objetivo es familiarizarnos con las coordenadas esféricas y con la geometría de la esfera, por lo que supondremos que la Tierra es esférica. En ese caso, la posición de cualquier pueblo de la Tierra puede expresarse mediante dos coordenadas, la latitud\(\phi\), medida al norte o al sur del ecuador, y la longitud\(λ\), medida hacia el este o hacia el oeste desde el meridiano a través de Greenwich. Estos símbolos,\(\phi\) para latitud y\(λ\) para longitud, son desafortunados, pero a menudo se utilizan en este contexto. En cuanto a los símbolos\(θ\),\(\phi\) para las coordenadas esféricas que hemos utilizado hasta ahora, correspondería la longitud este\(\phi\) y la latitud a\(90^\circ − θ\).

Un plano que cruza una esfera lo hace en círculo. Si ese plano pasa por el centro de la esfera (de manera que el centro del círculo es también el centro de la esfera), el círculo se llama un gran círculo. Todos los meridianos (los círculos de longitud fija que pasan por los polos norte y sur) incluyendo el que pasa por Greenwich, son grandes círculos, y también lo es el ecuador. Los planos que no pasan por el centro de la esfera (como los paralelos de latitud) son pequeños círculos. El radio de un paralelo de latitud es igual al radio de la esfera multiplicado por el coseno de la latitud.

Hemos utilizado el ejemplo de latitud y longitud en una Tierra esférica para ilustrar los conceptos de círculos grandes y pequeños. Si bien no es esencial perseguirla en el presente contexto, mencionamos de pasada que la verdadera figura de la Tierra a nivel medio del mar es un geoide -que simplemente significa la forma de la Tierra. A una buena aproximación, el geoide es un esferoide oblato (es decir, una elipse girada alrededor de su eje menor) con semieje mayor\(a = 6378.140 \ \text{km}\) y semieje menor\(c = 6356.755 \text{ km}\). La relación\((a−c)/a\) se llama elipticidad geométrica de la Tierra y tiene el valor\(1/298.3\). El radio medio de la Tierra, en el sentido del radio de una esfera que tiene el mismo volumen que el geoide real, es a\(\sqrt[3]{a^2 c} = 6371.00 \text{ km}\).

Es necesario en geodesia precisa distinguir entre la latitud geográfica o geodésica\(\phi\) de un punto de la superficie terrestre y su latitud geocéntrica\(\phi^\prime\). Sus definiciones son evidentes a partir de la figura\(\text{III.7}\). En esta figura, la elipticidad de la Tierra es muy exagerada; en realidad apenas sería discernible. El ángulo\(\phi\) es el ángulo entre una ploma-bob y el ecuador. Esto difiere\(\phi^\prime\) en parte porque el campo gravitacional de un esferoide no es el mismo que el de una masa puntual igual en el centro, y en parte porque la plomada se aleja del eje de rotación de la Tierra por la fuerza centrífuga.

\(\text{FIGURE III.7}\)

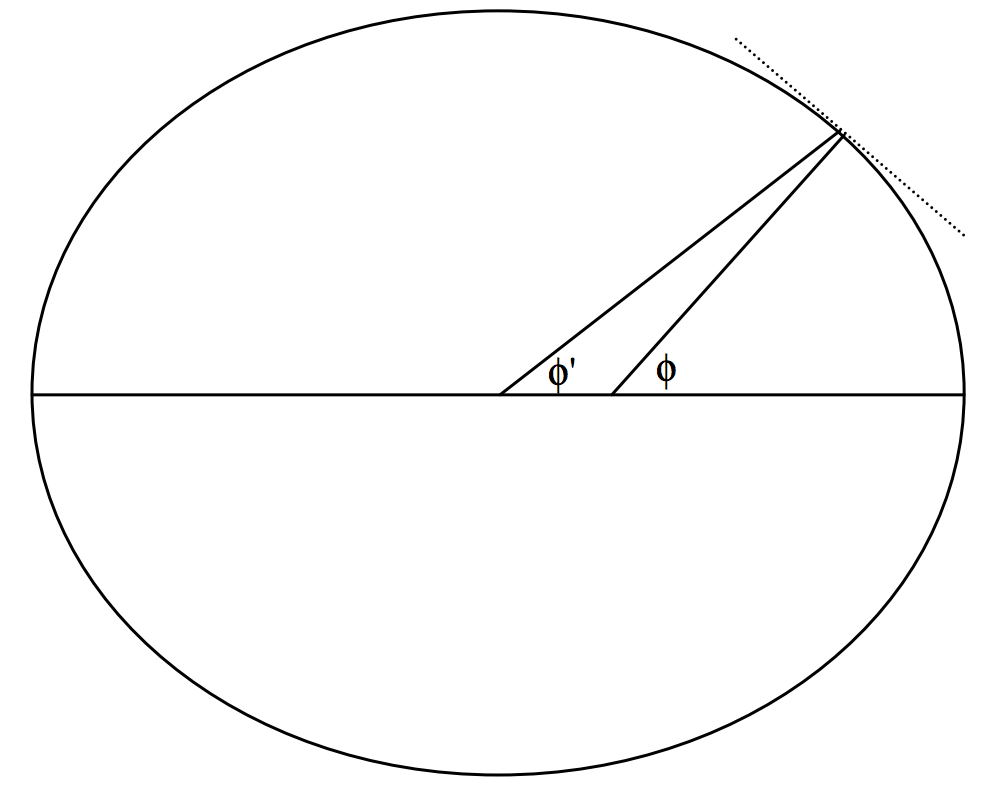
La relación entre\(\phi\) y\(\phi^\prime\) es

\[\phi - \phi^\prime = 692^\prime . 74 \sin 2 \phi - 1^\prime .16 \sin 4 \phi .\]