3.4: Componentes de velocidad y aceleración

Coordenadas polares bidimensionales

A veces los símbolos\(r\) y se\(θ\) utilizan para coordenadas polares bidimensionales, pero en esta sección utilizo\((ρ , \phi)\) para consistencia con las\((r, θ, \phi)\) de coordenadas esféricas tridimensionales. En lo que sigue estoy configurando vectores en\(\textbf{boldface}\). Si haces una impresión, debes tener en cuenta que algunas impresoras aparentemente no imprimen símbolos de letras griegas en negritas, aunque aparezcan en negritas en pantalla. Deberías estar al pendiente de esto. Los símbolos con ^ encima de ellos están pensados como vectores unitarios, por lo que sabrás que deben estar en negritas aunque tu impresora no lo reconozca. En caso de duda, mira lo que aparece en la pantalla.

\(\text{FIGURE III.8}\)

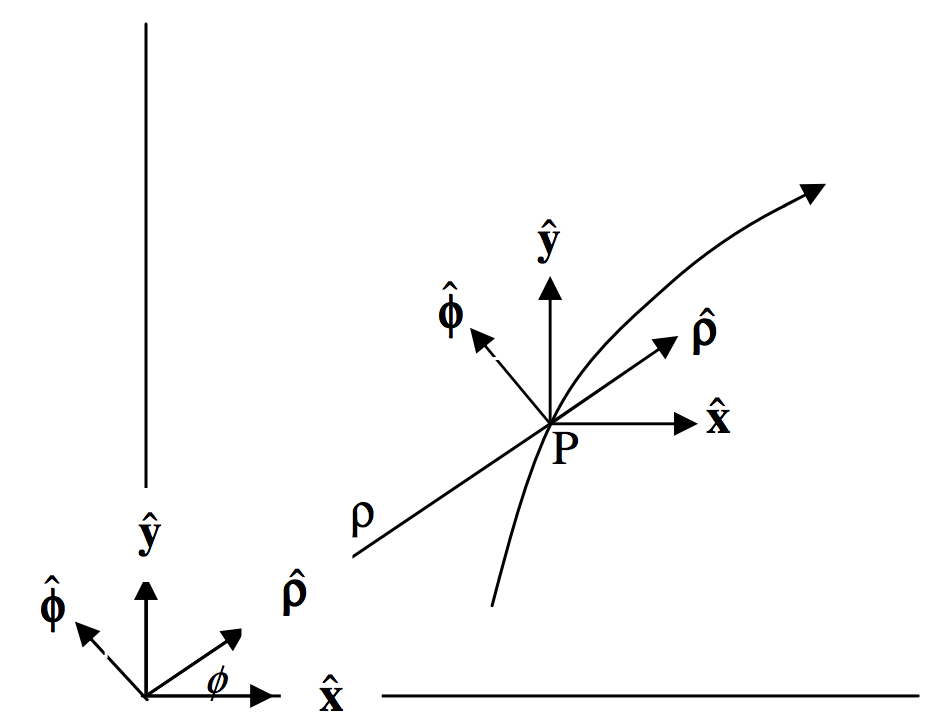
La figura\(\text{III.8}\) muestra un punto\(\text{P}\) moviéndose a lo largo de una curva tal que sus coordenadas polares están cambiando a velocidades\(\dot{ρ}\) y\(\dot{\phi}\). El dibujo también muestra vectores unitarios fijos \(\hat{x}\)y \(\hat{y}\)paralelos a los ejes\(x\) - y\(y\) -ejes, así como vectores unitarios \(\hat{\rho}\)y \(\hat{\phi}\)en las direcciones radial y transversal. Encontraremos expresiones para la velocidad a la que los vectores radiales y transversales unitarios están cambiando con el tiempo. (Al ser vectores unitarios, sus magnitudes no cambian, pero sus direcciones sí.)

Tenemos\[\boldsymbol{\hat{\rho}} = \cos \phi \boldsymbol{\hat{x}} + \sin \phi \boldsymbol{\hat{y}} \label{3.4.1} \tag{3.4.1}\]

y\[\boldsymbol{\hat{\phi}} = -\sin \phi \boldsymbol{\hat{x}} + \cos \phi \boldsymbol{\hat{y}}. \label{3.4.2} \tag{3.4.2}\]

\[\therefore \quad \boldsymbol{\dot{\rho}} = - \sin \phi \dot{\phi} \boldsymbol{\hat{x}} + \cos \phi \dot{\phi} \boldsymbol{\hat{y}} = \dot{\phi} (-\sin \phi \boldsymbol{\hat{x}} + \cos \phi \boldsymbol{\hat{y}}) \label{3.4.3} \tag{3.4.3}\]

\[\therefore \quad \boldsymbol{\hat{\rho}} = \dot{\phi} \boldsymbol{\hat{\phi}} \label{3.4.4} \tag{3.4.4}\]

De manera similar, diferenciando\(\ref{3.4.2}\) Ecuación. con respecto al tiempo y luego haciendo uso de la Ecuación\(\ref{3.4.1}\), encontramos

\[\boldsymbol{\dot{\hat{\phi}}} = - \dot{\phi} \boldsymbol{\hat{\rho}} \tag{3.4.5} \label{3.4.5}\]

Ecuaciones\(\ref{3.4.4}\) y\(\ref{3.4.5}\) dan la tasa de cambio de los vectores unitarios radiales y transversales. Vale la pena pensar detenidamente en lo que significan estas dos Ecuaciones.

El vector de posición del punto\(\text{P}\) puede ser representado por la expresión\(\boldsymbol{\rho} = \rho \boldsymbol{\hat{\rho}}\). La velocidad de\(\text{P}\) se encuentra diferenciando esto con respecto al tiempo:

\[\textbf{v} = \boldsymbol{\dot{\rho}} = \dot{\rho} \boldsymbol{\hat{\rho}} +\rho \boldsymbol{\dot{\hat{\rho}}} = \dot{\rho} \boldsymbol{\hat{\rho}} + \rho \dot{\phi} \boldsymbol{\hat{\phi}}. \label{3.4.6} \tag{3.4.6}\]

Los componentes radial y transversal de la velocidad son por lo tanto\(\dot{\phi}\) y\(\rho \dot{\phi}\) respectivamente. La aceleración se encuentra por diferenciación de Ecuación\(\ref{3.4.6}\), y tenemos que diferenciar los productos de dos y de tres cantidades que varían con el tiempo:

\ begin {array} {c c c c l}
\ textbf {a} & = &\ punto {\ textbf {v}} & = &\ ddot {\ rho}\ boldsymbol {\ hat {\ rho}} +\ punto {\ rho}\ símbolo en negrita {\ punto {\ sombrero {\ rho}} +\ punto {\ rho}\ punto {\ phi}\ negritasímbolo {\ sombrero {\ phi}} +\ rho\ ddot {\ phi}\ símbolo en negrita {\ sombrero {\ phi}} +\ rho\ punto {\ phi}\ símbolo en negrita {\ punto {\ sombrero {\ phi}}}\ \
&&& = &\ ddot {\ rho}\ negridsymbol {\ hat {\ rho}} +\ punto {\ rho}\ punto {\ phi}\ boldsymbol {\ hat {\ phi}} +\ punto {\ rho}\ punto {\ phi}\ boldsymbol {\ hat {\ phi}} +\ rho\ ddot {\ phi}\ boldsymbol {\ hat {\ phi}} -\ rho\ punto {\ phi} ^2\ negridsymbol {\ hat {\ rho}}\\
&&& = &\ left (\ ddot {\ rho} -\ rho\ punto {\ phi} ^2\ derecha)\ negridsymbol {\ sombrero {\ rho}} +\ izquierda (\ rho\ ddot {\ phi} + 2\ punto {\ rho}\ punto {\ phi}\ derecha)\ negritasímbolo {\ sombrero {\ phi}}. \
\ tag {3.4.7}\ label {3.4.7}
\ end {array}

Los componentes radial y transversal de la aceleración son por lo tanto\((\ddot{\rho} − \rho \dot{\phi}^2)\) y\((\rho \ddot{\phi} + 2 \dot{\rho} \dot{\phi})\) respectivamente.

Coordenadas esféricas tridimensionales

En la figura\(\text{III.9}\),\(\text{P}\) es un punto que se mueve a lo largo de una curva tal que sus coordenadas esféricas están cambiando a velocidades\(\dot{r}, \dot{θ}, \dot{\phi}\). Queremos saber qué tan rápido están cambiando los vectores unitarios\(\hat{\textbf{r}}\)\(\boldsymbol{\hat{\theta}}\),,\(\boldsymbol{\hat{\phi}}\) en las direcciones radial, meridional y acimutal.

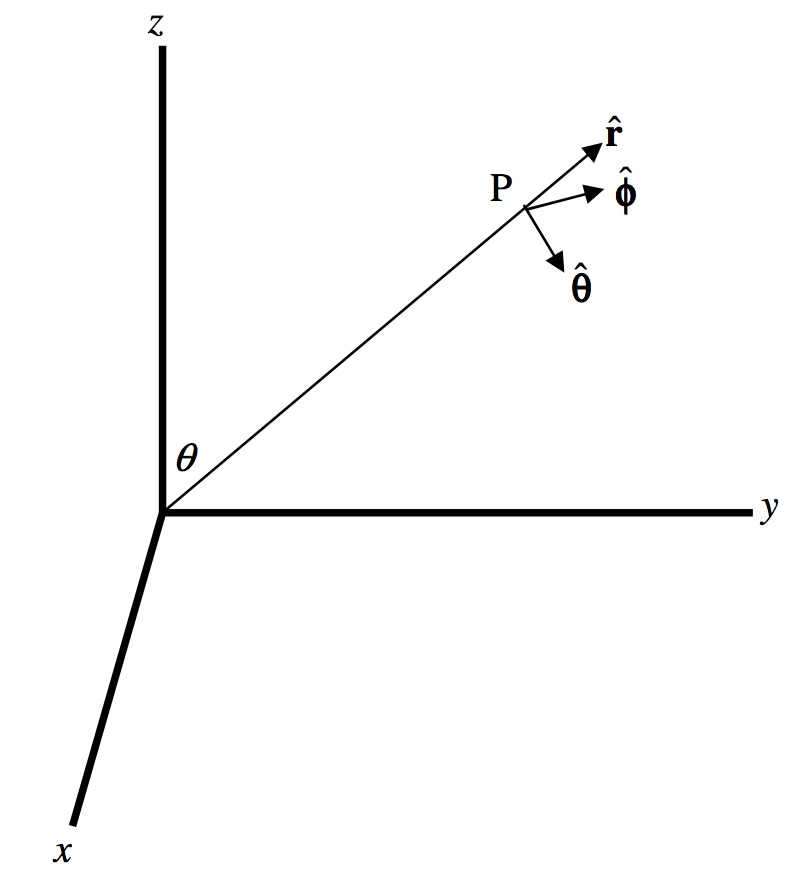
\(\text{FIGURE III.9}\)

Tenemos\[\hat{\textbf{r}} = \sin θ \cos \phi \hat{\textbf{x}} + \sin θ \sin \phi \hat{\textbf{y}} + \cos θ \hat{\textbf{z}} \label{3.4.8} \tag{3.4.8}\]

\[\boldsymbol{\hat{\theta}} = \cos θ \cos \phi \hat{\textbf{x}} + \cos θ \sin \phi \hat{\textbf{y}} - \sin θ \hat{\textbf{z}} \label{3.4.9} \tag{3.4.9}\]

\[\boldsymbol{\hat{\phi}} = - \sin \phi \hat{\textbf{x}} + \cos \phi \hat{\textbf{y}} \label{3.4.10} \tag{3.4.10}\]

\[\therefore \quad \hat{\textbf{r}} = (\cos θ \dot{θ} \cos \phi - \sin θ \sin \phi \dot{\phi} ) \hat{\textbf{x}} + (\cos θ \dot{θ} \sin \phi + \sin θ \cos \phi \dot{\phi} ) \hat{\textbf{y}} - \sin θ \dot{θ} \hat{\textbf{z}}. \label{3.4.11} \tag{3.4.11}\]

Vemos, comparando esto con Ecuaciones\(\ref{3.4.9}\) y\(\ref{3.4.10}\) que

\[\dot{\hat{\textbf{r}}} = \dot{θ} \boldsymbol{\hat{\theta}} + \sin θ \dot{\phi} \boldsymbol{\hat{\phi}} \label{3.4.12} \tag{3.4.12}\]

Por argumentos similares encontramos que

\[\boldsymbol{\dot{\hat{\theta}}} = \cos θ \dot{\phi} \boldsymbol{\hat{\phi}} - \dot{θ} \hat{\textbf{r}} \label{3.4.13} \tag{3.4.13}\]

y

\[\boldsymbol{\dot{\hat{\phi}}} = - \sin θ \dot{\phi} \hat{\textbf{r}} - \cos θ \dot{\phi} \boldsymbol{\hat{\theta}} \label{3.4.14} \tag{3.4.14}\]

Estas son las tasas de cambio de los vectores unitarios radiales, meridionales y acimutales. El vector de posición del punto\(\text{P}\) puede ser representado por la expresión\(\textbf{r} = r \ \hat{\textbf{r}}\). La velocidad de\(\text{P}\) se encuentra diferenciando esto con respecto al tiempo:

\ begin {array} {c c c}
\ textbf {v} & = &\ punto {\ textbf {r}} =\ punto {r}\ sombrero {\ textbf {r}} + r\ punto {\ sombrero {\ textbf {r}}} =\ punto {r}\ sombrero {r} + r (\ punto {θ}\ símbolo negrita {\ sombrero {\ sombrero {\ theta}} +\ sin θ\ punto {\ phi}\ símbolo en negrita {\ sombrero {\ phi}})\\
& = &\ punto {r}\ sombrero {\ textbf {r}} + r\\ punto {θ}\ boldsymbol {\ hat {\ theta}} + r\ sin θ\ punto {\ phi}\ boldsymbol {\ hat {\ phi}}\
\ etiqueta {3.4.15}\ tag {3.4.15}
\ end {array}

Los componentes radial, meridional y azimutal de la velocidad son por lo tanto\(\dot{r}, \ r \dot{θ}\) y\(r \sin θ \dot{\phi}\) respectivamente.

La aceleración se encuentra por diferenciación de Ecuación\(\ref{3.4.15}\).

Puede que no esté fuera de lugar aquí para una pista rápida sobre la diferenciación. La mayoría de los lectores sabrán diferenciar un producto de dos funciones. Si se quiere diferenciar un producto de varias funciones, por ejemplo cuatro funciones,\(a, \ b, \ c\) y\(d\), el procedimiento es

\((abcd)^\prime = a^\prime bcd + ab^\prime cd + abc^\prime d + abcd^\prime\).

En el último término de la Ecuación\(\ref{3.4.15}\), las cuatro cantidades varían con el tiempo, y estamos a punto de diferenciar el producto.

\[\textbf{a} = \dot{\textbf{v}} = \ddot{r} \hat{\textbf{r}} + \dot{r} ( \dot{θ} \boldsymbol{\hat{\theta}} + \sin θ \dot{\phi} \boldsymbol{\hat{\phi}}) + \dot{r} \dot{θ} \boldsymbol{\hat{\theta}} + r \ddot{\theta} \boldsymbol{\hat{\theta}} + r \dot{θ} ( \cos θ \dot{\phi} \boldsymbol{\hat{\phi}} - \dot{θ} \hat{\textbf{r}} ) + \dot{r} \sin θ \dot{\phi} \boldsymbol{\hat{\phi}} + r \cos θ \dot{θ} \dot{\phi} \boldsymbol{\hat{\phi}} + r \sin θ \ddot{\phi} \boldsymbol{\hat{\phi}} + r \sin θ \dot{\phi} ( - \sin θ \dot{\phi} \hat{\textbf{r}} - \cos θ \dot{\phi} \boldsymbol{\hat{\theta}}) \tag{3.4.16} \label{3.4.16}\]

Al reunir los coeficientes de\(\hat{\textbf{r}}, \boldsymbol{\hat{\theta}}, \boldsymbol{\hat{\phi}}\), encontramos que los componentes de la aceleración son:

• Radiales:\(\ddot{r} - r \dot{θ}^2 - r \sin^2 θ \dot{\phi}^2 \)
• Meridional:\(r \ddot{θ} + 2\dot{r} \dot{θ} - r \sin θ \cos θ \dot{\phi}^2 \)
• Azimutal:\(2 \dot{r} \dot{\phi} \sin θ + 2r \dot{θ} \dot{\phi} \cos θ + r \sin θ \ddot{\phi}\)

Colaborador

• Template:ContribTatum