3.5: Triángulos esféricos

Al igual que con los triángulos planos, denotamos los tres ángulos por\(A, \ B, \ C\) y los lados opuestos a ellos por\(a, \ b, \ c\). Tenemos la suerte de que tenemos a nuestra disposición cuatro fórmulas para la solución de un triángulo esférico, y, como ocurre con los triángulos planos, el arte de resolver un triángulo esférico implica entender qué fórmula es apropiada en determinadas circunstancias. Cada fórmula contiene cuatro elementos (lados y ángulos), tres de los cuales, en un problema dado, se supone que son conocidos, y el cuarto está por determinar.

Hay que anotar tres puntos importantes antes de anotar las fórmulas.

1. Las fórmulas son válidas sólo para triángulos en los que los tres lados son arcos de grandes círculos. No van a hacer, por ejemplo, para un triángulo en el que un lado es un paralelo de latitud.
2. Los lados de un triángulo esférico, así como los ángulos, se expresan todos en medida angular (grados y minutos) y no en medida lineal (metros o kilómetros). Un lado de\(50^\circ\) significa que el lado es un arco de un gran círculo que subtiende un ángulo de\(50^\circ\) en el centro de la esfera.
3. La suma de los tres ángulos de un triángulo esférico suman más de\(180^\circ\).

En esta sección ahora se dan las cuatro fórmulas sin prueba, las derivaciones se dan en una sección posterior. Las cuatro fórmulas pueden denominarse fórmula sinusoidal, fórmula coseno, fórmula coseno polar y fórmula cotangente. Debajo de cada fórmula se muestra un triángulo esférico en el que se resaltan los cuatro elementos contenidos en la fórmula.

La fórmula sinusoidal:\[\frac{\sin a}{\sin A} = \frac{\sin b}{\sin B} \left( = \frac{\sin c}{\sin C} \right) \label{3.5.1} \tag{3.5.1}\]

\(\text{FIGURE III.10}\)

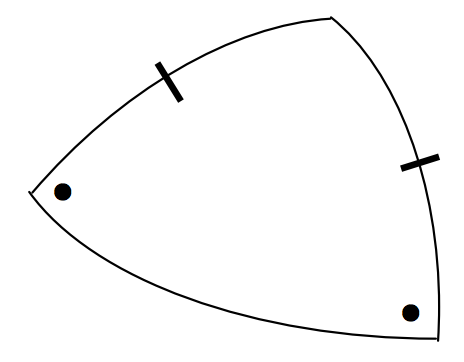
La fórmula del coseno:\[\cos a = \cos b \cos c + \sin b \sin c \cos A \label{3.5.2} \tag{3.5.2}\]

\(\text{FIGURE III.11}\)

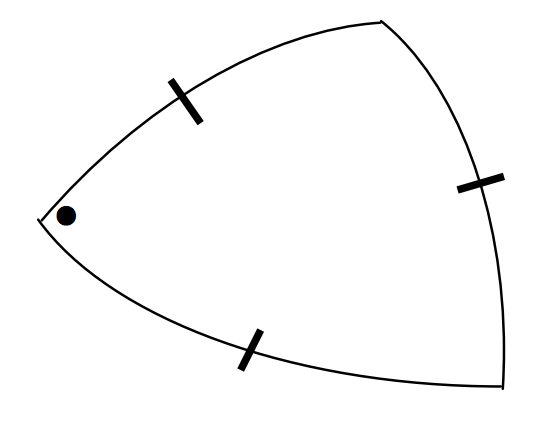
La fórmula del coseno polar:\[\cos A = - \cos B \cos C + \sin B \sin C \cos a \label{3.5.3} \tag{3.5.3}\]

\(\text{FIGURE III.12}\)

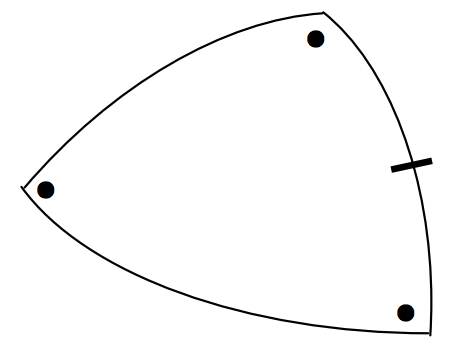
La fórmula cotangente:\[\cos b \cos A = \sin b \cot c - \sin A \cot C \label{3.5.4} \tag{3.5.4}\]

\(\text{FIGURE III.13}\)

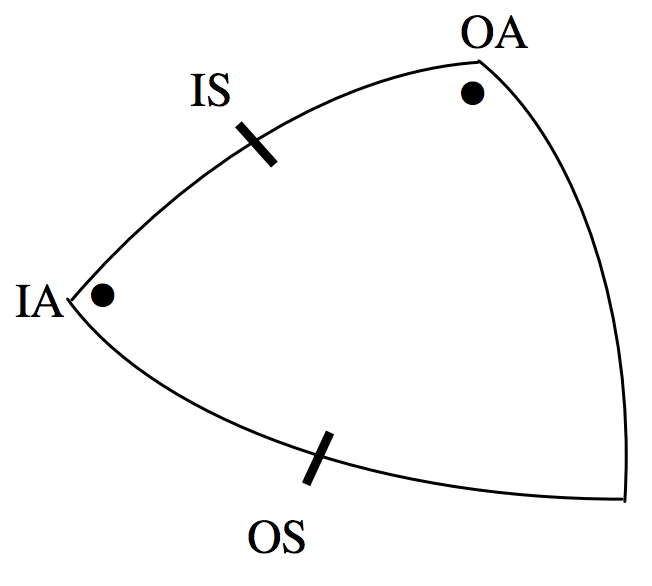
La fórmula cotangente es una fórmula particularmente útil y frecuentemente necesaria, y es lamentable que no sólo sea difícil comprometerse con la memoria sino que, incluso con la fórmula escrita frente a una, a menudo es difícil decidir cuál es\(b\), cuál es\(A\) y así sucesivamente. Sin embargo, cabe señalar a partir del dibujo que los cuatro elementos, ángulo lateral-ángulo lateral, se encuentran adyacentes entre sí en el triángulo, y pueden denominarse lado exterior (\(\text{OS}\)), ángulo interno (\(\text{IA}\)), lado interno (\(\text{IS}\)) y ángulo externo (\(\text{OA}\)) respectivamente. Mucha gente encuentra que la fórmula es mucho más fácil de usar cuando se escribe en el formulario

\[\cos (\text{IS}) \cos (\text{IA}) = \sin (\text{IS}) \cot (\text{OS}) - \sin (\text{IA}) \cot (\text{OA}) \label{3.5.5} \tag{3.5.5}\]

En breve se ofrecerá al lector una buena cantidad de ejemplos en el uso de estas fórmulas. Sin embargo, durante el transcurso del uso de las fórmulas, se encontrará que existe una necesidad frecuente de resolver ecuaciones trigonométricas engañosamente simples del tipo

\[4.737 \sin θ + 3.286 \cos θ = 5.296 \label{3.5.6} \tag{3.5.6}\]

Después quizás de una breve pausa, uno de varios métodos puede presentarse al lector, pero no todos los métodos son igualmente satisfactorios. Voy a sugerir cuatro posibles formas de resolver esta Ecuación. El primer método es aquel que le puede ocurrir muy rápidamente al lector por ser quizás bastante obvio -pero hay un cuento de precaución adjunto a él. Si bien el método puede parecer muy obvio, sí surge una dificultad, y se aconsejaría al lector que prefiera uno de los métodos menos obvios. Hay, por cierto, dos soluciones a la Ecuación entre\(0^\circ\) y\(360^\circ\). Ellos son\(31^\circ 58^\prime .6\) y\(78^\circ 31^\prime .5\).

Método i

El método obvio es aislar\(\cos θ\):

\[\cos θ = 1.611 \ 686 - 1.441 \ 570 \ \sin θ.\]

Si bien las constantes en el problema se dieron a cuatro cifras significativas, no se tiente a redondear los cálculos intermedios a cuatro. Es una falla común redondear prematuramente los cálculos intermedios. El redondaje se puede hacer al final.

Cuadrar ambos lados, y escribir el lado izquierdo,\(\cos^2 θ\), como\(1 − \sin^2 θ\). Ahora tenemos una Ecuación cuadrática en\(\sin θ\):

\[3.078 \ 125 \sin^2 θ - 4.646 \ 717 \sin θ + 1.597 \ 532 = 0. \]

Las dos soluciones para\(\sin θ\) son\(0.529 \ 579\) y\(0.908 \ 014\) y los cuatro valores de\(θ\) que satisfacen estos valores de\(\sin θ\) son\(31^\circ 58^\prime .6, \ 148^\circ \ 01^\prime .4, \ 78^\circ \ 31^\prime .5\) y\(101^\circ 28^\prime .5\).

Sólo dos de estos ángulos son soluciones de la Ecuación original. El movimiento fatal fue cuadrar ambos lados de la Ecuación original, de manera que hemos encontrado soluciones no solo para

\[\cos θ = 1.611 \ 686 - 1.441 \ 570 \sin θ\]

sino también a la diferente Ecuación

\[-\cos θ = 1.611 \ 686 - 1.441 \ 570 \ \sin θ.\]

Esta generación de soluciones extra siempre ocurre siempre que cuadramos una Ecuación. Por esta razón, se debe evitar el método (i), por muy tentador que sea, particularmente cuando se programa una computadora para realizar un cómputo de forma automática y acrítica.

En caso de duda si ha obtenido una solución correcta, sustituya su solución en la Ecuación original. Siempre debes hacer esto con cualquier Ecuación de cualquier tipo, de todos modos.

Método ii

Este método hace uso de las identidades

\[\sin θ = \frac{2t}{1+t^2}, \quad \cos θ = \frac{1-t^2}{1+t^2},\]

donde\(t = \tan \frac{1}{2} θ\).

Cuando se aplica a la Ecuación original, esto da como resultado la Ecuación cuadrática en\(t\):

\[8.582t^2 - 9.474t + 2.010 = 0\]

con soluciones\[t= 0.286528 \quad \text{and} \quad t = 0.817410\]

Los únicos valores de\(θ\) entre\(0^\circ\) y\(360^\circ\) que satisfacen estos son las dos soluciones correctas\(31^\circ \ 58^\prime .6\) y\(78^\circ \ 31^\prime .5\).

Se deja como ejercicio para mostrar, utilizando este método algebraicamente, que las soluciones a la Ecuación

\[a \sin θ + b \cos θ = c\]

están dadas por\[\tan \frac{1}{2} θ = \frac{a \pm \sqrt{a^2 + b^2 - c^2}}{b+ c}.\]

Esto demuestra que no hay soluciones reales si\(a^2 + b^2 < c^2\), una solución real si\(a^2 + b^2 = c^2\), y dos soluciones reales si\(a^2 + b^2 > c^2\).

Método iii

Dividimos la ecuación original

\[4.737 \sin θ + 3.286 \cos θ = 5.296\]

por la “hipotenusa” de\(4.737\) y\(3.286\); es decir, por\(\sqrt{(4.737^2 + 3.286^2)} = 5.765151\).

Por lo tanto\[0.821 \ 661 \ \sin θ + 0.569 \ 976 \cos θ = 0.918 \ 623 \]

Ahora vamos\(0.821 \ 661 = \cos α\) y\(0.569 976 = \sin α\) (que podemos, ya que estos números ahora satisfacen\(\sin^2 α \cos^2 α = 1\)) así que eso\(α = 34^\circ \ 44^\prime .91\).

Tenemos\[\cos α \sin θ + \sin α \cos θ = 0.918 \ 623 \]

o\[\sin(θ + α) = 0.918623\]

a partir de la cual\[θ + α = 66^\circ \ 43^\prime .54 \text{ or } 113^\circ \ 16^\prime .46\]

Por lo tanto\[θ = 31^\circ \ 58^\prime .6 \text{ or } 78^\circ \ 31^\prime .5\]

Método iv

Los métodos ii y iii dan soluciones explícitas, por lo que quizás no sea necesario utilizar métodos numéricos. Sin embargo, el lector podría querer resolver, mediante la iteración de Newton-Raphson, la Ecuación

\[f(θ) = a \sin θ + b \cos θ - c = 0,\]

para lo cual\[f^\prime ( θ ) = a \cos θ - b \sin θ.\]

Usando los valores de\(a, \ b\) y\(c\) del ejemplo anterior y usando el algoritmo Newton-Raphson, encontramos con una primera suposición de\(45^\circ\) las siguientes iteraciones, trabajando en radianes:

\ begin {array} {c c c}
0.785\ 398\
0.417\ 841\\
0.541\ 499\\
0.557\ 797\
0.558\ 104\
0.558\ 104 & = & 31^\ circ 58^\ prime .6\
\ final {array}

El lector debe verificar este cálculo y, usando una primera suposición diferente, mostrar que la iteración de NewtonRaphson conduce rápidamente a\(78^\circ \ 31^\prime .5\).

Habiendo ya despejado ese pequeño obstáculo, se invita al lector a resolver los problemas del triángulo esférico a continuación. Si bien estos doce problemas parecen un trabajo repetitivo sin sentido, de hecho son todos diferentes. Algunos tienen dos soluciones entre\(0^\circ\) y\(360^\circ\); otros tienen solo una. Después de resolver cada problema, el lector debe bosquejar cada triángulo -especialmente aquellos que tienen dos soluciones- para ver cómo surgen las ambigüedades dobles. El lector también debe escribir un programa de computadora que resuelva los doce tipos de problemas a puja del usuario. Las respuestas deben darse en grados, minutos y décimas de minuto, y deben ser correctas con esa precisión. Por ejemplo, la respuesta a uno de los problemas es\(47^\circ \ 37^\prime .3\). Una respuesta de\(47^\circ \ 37^\prime .2\) o\(47^\circ \ 37^\prime .4\) debe considerarse incorrecta. En la mecánica celeste, no hay lugar para respuestas que son “casi correctas”. Una respuesta es correcta o incorrecta. (Esto no significa, por supuesto, que se pueda medir un ángulo sin ningún error; pero la respuesta a un cálculo dado a una décima de minuto de arco debe ser correcta a una décima parte de un minuto de arco).

Ejercicio 1

Todos los ángulos y lados en grados

\ begin {array} {c c c c c}
10. & a=64 & b=33 & c=37 & C =? \\
11. & a=39 & b=48 & C=74 & c =? \\
12. & a=16 & b=37 & C=42 & B=? \\
13. & a=21 & b=43 & A=29 & c=? \\
14. & a=67 & b=54 & A=39 & B=? \\
15. & a=49 & b=59 & A=14 & C=? \\
16. & A=24 & B=72 & c=19 & a=? \\
17. & A=79 & B=84 & c=12 & C=? \\
18. & A=62 & B=49 & a=44 & b=? \\
19. & A=59 & B=32 & a=62 & c=? \\
20. & A=47 & B=57 & a=22 & C=? \\
21. & A=79 & B=62 & C=48 & c=? \\
\ fin {matriz}

Soluciones

10. \(28^\circ 18^\prime .2\)
11. \(49^\circ 32^\prime .4\)
12. \(117^\circ 31^\prime .0\)
13. \(30^\circ 46^\prime .7 \text{ or } 47^\circ 37^\prime .3\)
14. \(33^\circ 34^\prime .8\)
15. \(3^\circ 18^\prime .1 \text{ or } 162^\circ 03^\prime .9\)
16. \(7^\circ 38^\prime .2\)
17. \(20^\circ 46^\prime .6\)
18. \(36^\circ 25^\prime .5\)
19. \(76^\circ 27^\prime .7\)
20. \(80^\circ 55^\prime .7 \text{ or } 169^\circ 05^\prime .2\)
21. \(28^\circ 54^\prime .6\)

Derivación de las fórmulas

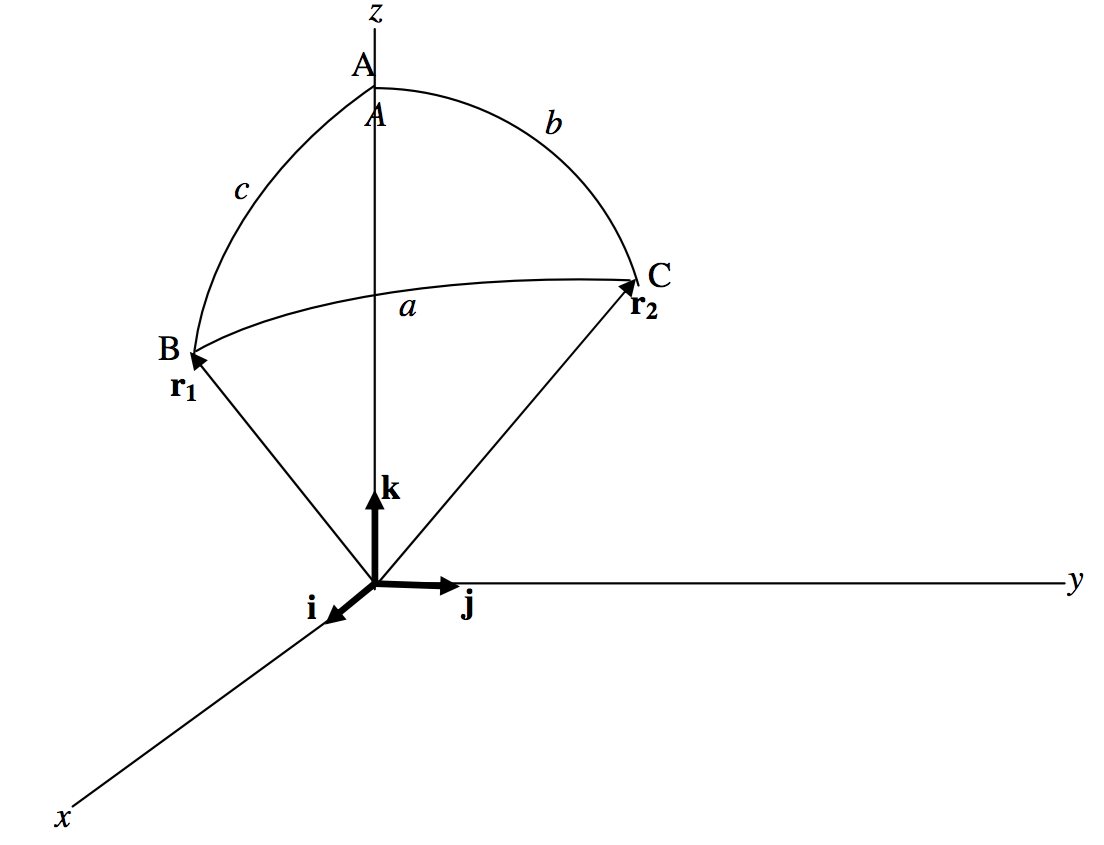
Antes de pasar a más problemas y aplicaciones de las fórmulas, es momento de derivar las cuatro fórmulas que, hasta ahora, acababan de darse sin pruebas. Comenzamos con la fórmula coseno. No hay pérdida de generalidad en la elección de ejes rectangulares de tal manera que el punto\(\text{A}\) del triángulo esférico\(\text{ABC}\) está en el\(z\) eje -y el punto\(\text{B}\) y por lo tanto el lado\(c\) están en el\(zx\) -plano. Se supone que la esfera es de radio unitario.

\(\text{FIGURE III.14}\)

Si\(\textbf{i}, \ \textbf{j}\) y\(\textbf{k}\) son vectores unitarios dirigidos a lo largo de\(z\) los ejes\(x\)\(y\) −, − y −respectivamente, la inspección de la figura mostrará que los vectores de posición de los puntos\(\text{B}\) y\(\text{C}\) con respecto al centro de la esfera son

\[\textbf{r}_1 = \textbf{i} \sin c + \textbf{k} \cos c \label{3.5.7} \tag{3.5.7}\]

y\[\textbf{r}_2 = \textbf{i} \sin b \cos A + \textbf{j} \sin b \sin A + \textbf{k} \cos b \label{3.5.8} \tag{3.5.8}\]

respectivamente.

El producto escalar de estos vectores (cada uno de unidad de magnitud) es solo el coseno del ángulo entre ellos, es decir\(\cos a\), del que obtenemos inmediatamente

\[\cos a = \cos b \cos c + \sin b \sin c \cos A. \label{3.5.9} \tag{3.5.9}\]

Para obtener la fórmula sinusoidal, aislamos\(\cos A\) de esta Ecuación, cuadramos ambos lados, y escribimos\(1 − \sin^2 A\) para\(\cos^2 A\). Por lo tanto,

\[(\sin b \sin c \cos A )^2 = (\cos a - \cos b \cos c )^2 , \label{3.5.10} \tag{3.5.10}\]

y cuando hayamos realizado estas operaciones obtenemos

\[\sin^2 A = \frac{\sin^2 b \sin^2 c - \cos^2 a - \cos^2 b \cos^2 c + 2\cos a \cos b \cos c}{\sin^2 b \sin^2 c} . \label{3.5.11} \tag{3.5.11}\]

En el numerador, escribe\(1 − \cos^2 b\) para\(\sin^2 b\) y\(1 − \cos^2 c\) para\(\sin^2 c\), y divide ambos lados por\(\sin^2 a\). Esto da como resultado

\[\frac{\sin^2 A}{\sin^2 a} = \frac{1-\cos^2 a - \cos^2 b - \cos^2 c + 2\cos a \cos b \cos c}{\sin^2 a \sin^2 b \sin^2 c}. \label{3.5.12} \tag{3.5.12}\]

En esta etapa el lector puede sentir que nos estamos empantanando en álgebra cada vez más pesada y no llegando a ninguna parte. Pero, después de una mirada cuidadosa a Ecuación\(\ref{3.5.12}\), se puede notar con cierto deleite que la siguiente línea es:

Por lo tanto\[\frac{\sin A}{\sin a} = \frac{\sin B}{\sin b} = \frac{\sin C}{\sin c}. \label{3.5.13} \tag{3.5.13}\]

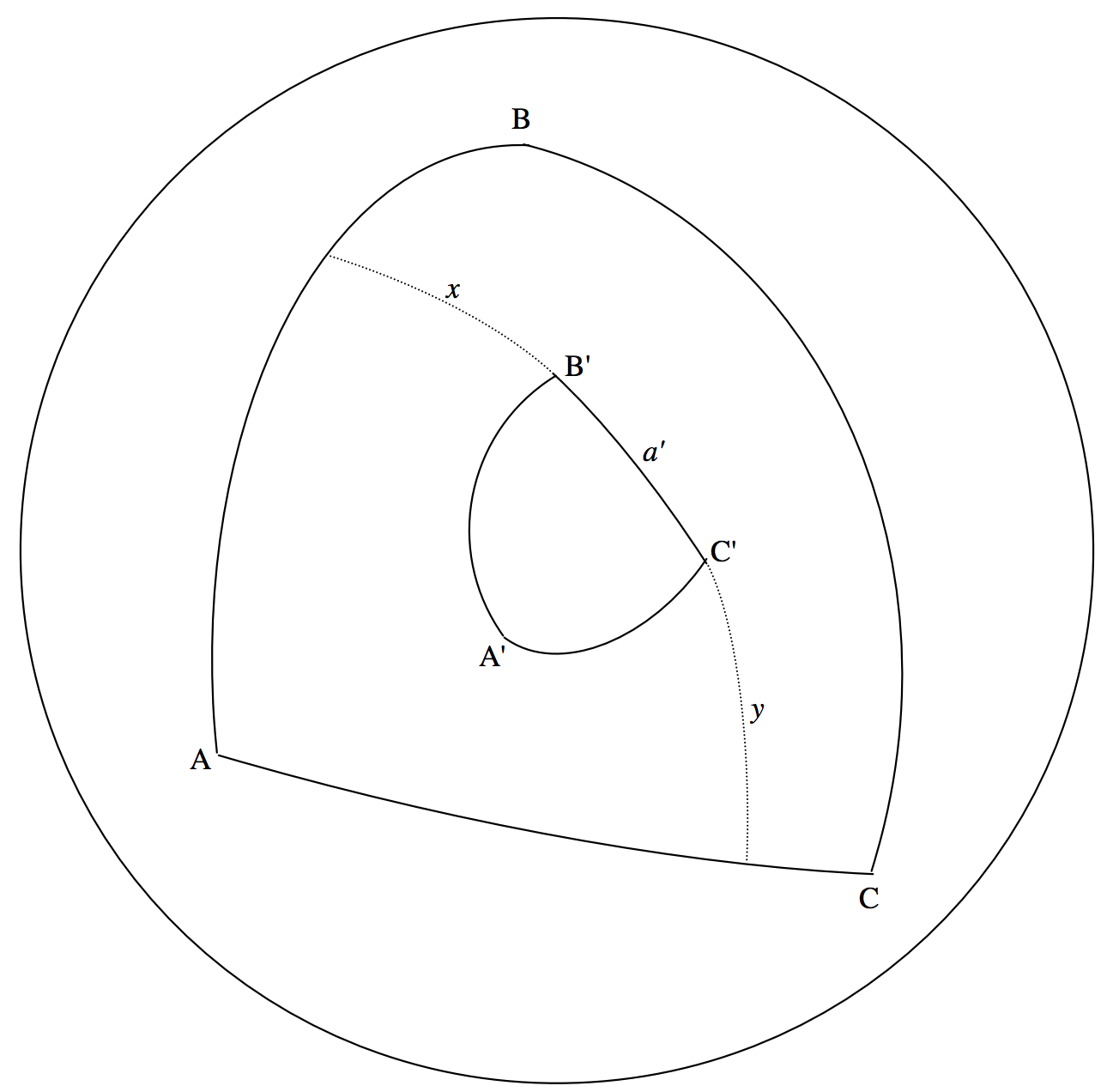
La derivación de la fórmula del coseno polar también puede traer un pequeño momento de deleite. En la figura\(\text{III.15}\),\(\text{A}^\prime \text{B}^\prime \text{C}^\prime\) es un triángulo esférico. \(\text{ABC}\)es también un triángulo esférico, llamado el triángulo polar a\(\text{A}^\prime \text{B}^\prime \text{C}^\prime\). Se forma de la siguiente manera. El lado\(\text{BC}\) es un arco de un gran círculo\(90^\circ\) desde\(\text{A}^\prime\); es decir,\(\text{BC}\) forma parte del ecuador del cual\(\text{A}^\prime\) es polo. Del mismo modo\(\text{CA}\) es\(90^\circ\) de\(\text{B}^\prime\) y\(\text{AB}\) es\(90^\circ\) de\(\text{C}^\prime\). En el dibujo, el lado\(\text{B}^\prime \text{C}^\prime\) del triángulo pequeño se ha extendido para encontrarse con los lados\(\text{AB}\) y\(\text{CA}\) del triángulo grande. Será evidente a partir del dibujo que el ángulo\(A\) de los grandes

\(\text{FIGURE III.15}\)

triángulo es igual a\(x + a^\prime + y\). Además, a partir de la forma en que\(\text{ABC}\) se formó el triángulo,\(x+ a^\prime\) y\(a^\prime + y\) son cada uno igual a\(90^\circ\). A partir de estas relaciones, vemos que

\[A + A = [(x + a^\prime) + y] + [x + (a^\prime + y)]\]

o\[2A = 180^\circ + x + y = 180^\circ + A - a^\prime \]

Por lo tanto\[A = 180^\circ - a^\prime\]

De manera similar,\[B = 180^\circ - b^\prime \text{ and } C = 180^\circ - c^\prime\]

Ahora, supongamos que\(f(A^\prime, B^\prime, C^\prime, a^\prime, b^\prime, c^\prime) = 0\) hay alguna relación entre los lados y los ángulos del triángulo\(\text{A}^\prime \text{B}^\prime \text{C}^\prime\). Podemos sustituir\(a^\prime\)\(180^\circ − A, \ b^\prime\) por\(180^\circ − B\), y así sucesivamente, y esto dará como resultado una relación entre\(A, \ B, \ C, \ a, \ b\) y\(c\); es decir, resultará en una relación entre los lados y ángulos del triángulo\(\text{ABC}\).

Por ejemplo, la Ecuación

\[\cos a^\prime = \cos b^\prime \cos c^\prime + \sin b^\prime \sin c^\prime \cos A^\prime \label{3.5.14} \tag{3.5.14}\]

es válido para el triángulo\(\text{A}^\prime \text{B}^\prime \text{C}^\prime\). Al hacer estas sustituciones, encontramos la siguiente fórmula válida para triángulo\(\text{ABC}\):

\[- \cos A = \cos B \cos C - \sin B \sin C \cos a, \label{3.5.15} \tag{3.5.15}\]

que es la fórmula del coseno polar.

Sin duda, al lector le gustará intentar partir de las fórmulas sinusoidal y cotangente para el triángulo\(\text{A}^\prime \text{B}^\prime \text{C}^\prime\) y deducir las correspondientes fórmulas polares para el triángulo\(\text{ABC}\), aunque esto, lamentablemente, puede dar lugar a alguna decepción anticlimática.

No conozco ninguna derivación particularmente interesante de la fórmula cotangente, y dejo al lector trabajar a través del álgebra más bien peatonal. Empezar desde

\[\cos a = \cos b \cos c + \sin b \sin c \cos A\]

y\[\cos c = \cos a \cos b + \sin a \sin b \cos C.\]

Eliminar\(\cos c\) (pero retener\(\sin c\)) de estas Ecuaciones, y escribir\(1 − \sin^2 b\) para\(\cos^2 b\). Finalmente sustituir\(\frac{\sin c \sin A}{\sin C}\)\(\sin a\), y, después de un poco de ordenar, debería resultar la fórmula cotangente.

En esta etapa, hemos tenido cierta práctica en la solución de las cuatro fórmulas triangulares esféricas, y las hemos derivado. En esta sección nos encontramos con ejemplos en los que el problema no es simplemente resolver un triángulo, sino adquirir algo de experiencia en la configuración de un problema y decidir qué triángulo tiene que resolverse.

Ejemplo 1

Las coordenadas del Observatorio Astrofísico Dominion, cerca de Victoria, Columbia Británica, son

Latitud\(48^\circ 31^\prime .3 \text{N}\) Longitud\(123^\circ 25^\prime .0 \text{W}\)

y las coordenadas del Observatorio David Dunlap, cerca de Toronto, Ontario, son

Latitud\(43^\circ 51^\prime .8 \text{N}\) Longitud\( 79^\circ 25^\prime .3 \text{W}\)

¿A qué distancia está Toronto de Victoria, y cuál es el acimut de Toronto respecto a Victoria?

El triángulo a dibujar y resolver es el triángulo\(\text{PVT}\), donde\(\text{P}\) está el polo norte de la Tierra,\(\text{V}\) es Victoria, y\(\text{T}\) es Toronto. En la figura\(\text{III.16}\) se marcan las colatitudes de las dos ciudades y la diferencia entre sus longitudes.

La gran distancia circular\(ω\) entre los dos observatorios viene dada fácilmente por la fórmula coseno:

\[\cos ω = \cos 41^\circ 28^\prime .7 \cos 46^\circ 08^\prime .2 + \sin 41^\circ 28^\prime .7 \sin 46^\circ 08^\prime .2 \cos 43^\circ 59^\prime .7\]

A partir de esto, encontramos\(ω = 30^\circ 22^\prime .7\) o\(0.53021\) radianes. El radio de la Tierra es\(6371 \ \text{km}\), por lo que la distancia entre los observatorios es\(3378 \ \text{km}\) o\(2099\) millas.

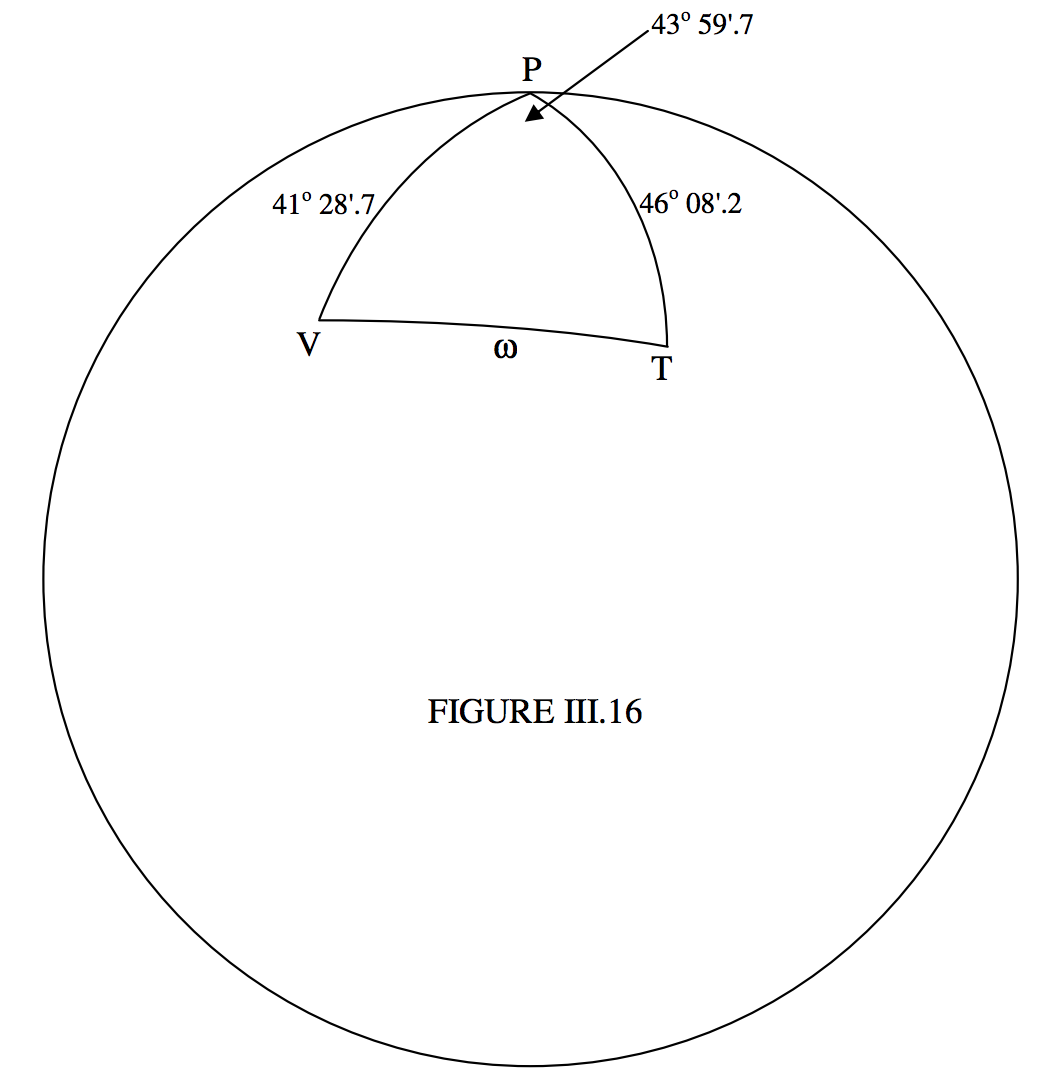
Ahora que hemos encontrado\(ω\), podemos encontrar el acimut, que es el ángulo\(V\), a partir de la fórmula sinusoidal:

\[\sin V = \frac{\sin 46^\circ 08^\prime .2 \ \sin 43^\circ 59^\prime .7}{\sin 30^\circ 22^\prime .7} = 0.990 \ 275\]

y por lo tanto\[V = 82^\circ 00^\prime .3\]

Pero ahora debemos recordar que\(\sin^{-1} 0.990 \ 275\) tiene dos valores entre\(0^\circ\) y\(180^\circ\), a saber,\(82^\circ 00^\prime .3\) y\(97^\circ 59^\prime .7\).

Por lo general, es obvio a partir de la inspección de un dibujo cuál de los dos valores de\(\sin^{-1}\) es el requerido. Desafortunadamente, en este caso, ambos valores están cerca\(90^\circ\), y puede que no sea inmediatamente obvio cuál de los dos valores requerimos. No obstante, se notará que Toronto tiene una latitud más meridional que Victoria, y esto debería resolver fácilmente la ambigüedad.

Podríamos, por supuesto, haber encontrado el acimut\(V\) usando la fórmula cotangente, sin tener que calcular\(ω\) primero. Así

\[\cos 41^\circ 28^\prime .7 \cos 43^\circ 59^\prime .7 = \sin 41^\circ 28^\prime .7 \cot 46^\circ 08^\prime .2 - \sin 43^\circ 59^\prime .7 \cot V\]

Sólo hay una solución para\(V\) entre\(0^\circ\) y\(180^\circ\), y es la correcta, a saber\(82^\circ 00^\prime .3\). Un buen dibujo le mostrará al lector por qué la solución correcta fue el ángulo agudo más que el obtuso (en nuestro dibujo el ángulo se hizo para estar cerca para\(90^\circ\) no sesgar al lector de una manera u otra), sino en cualquier caso a todos los lectores, especialmente a aquellos que quedaron atrapados en elegir el ángulo obtuso , deben tomar atenta nota de las dificultades que pueden ocasionar la ambigüedad de la función\(\sin^{-1}\). En efecto, es el firme consejo del autor el no usar nunca la fórmula sinusoidal, a pesar de la facilidad de memorizarla. La fórmula cotangente es más difícil de comprometer con la memoria, pero es mucho más útil y no tan propensa a errores de cuadrante.

Ejemplo 2

Considera dos puntos\(\text{B}\),\(\text{A}\) y, en latitud\(20^\circ \text{N}\)\(25^\circ \text{E}\), longitud y latitud\(72^\circ \text{N}\), longitud\(44^\circ \text{E}\). ¿Dónde están los polos del gran círculo pasando por estos dos puntos? Presentaremos dos métodos para hacer el problema. Primero, resolviendo triángulos esféricos. Y segundo, amablemente me sugirió Achintya Pal, utilizando los métodos de geometría de coordenadas algebraicas.

Llamemos a la colatitud y longitud del primer punto\((θ_1 , \phi_1)\) y del segundo punto\((θ_2, \phi_2)\) Consideraremos la pregunta respondida si podemos encontrar las coordenadas\((θ_0, \phi_0)\) de los polos\(\text{Q}\) y\(\text{Q}^\prime\) del gran círculo que pasa por los dos puntos. En figura\(\text{III.17}\),\(\text{P}\) es el polo norte de la Tierra,\(\text{A}\) y\(\text{B}\) son los dos puntos en cuestión, y\(\text{Q}\) es uno de los dos polos del gran círculo uniéndose\(\text{A}\) y\(\text{B}\). La figura también muestra el triángulo\(\text{PQA}\). Supondremos que el origen de las longitudes (“Greenwich”) está detrás del plano del papel. Las longitudes orientales de\(\text{Q}\),\(\text{A}\) y\(\text{B}\) son, respectivamente,\(\phi_0, \phi_1, \phi_2\); y sus colatitudes son\(θ_0 , θ_1 ,θ_2\).

\[0=\cos θ_0 \cos θ_1 + \sin θ_0 \sin θ_1 \cos (\phi_1 - \phi_0), \label{3.5.16} \tag{3.5.16}\]

de la cual

\[\tan θ_0 = -\frac{1}{\tan θ_1 \cos (\phi_1 - \phi_0)}. \label{3.5.17} \tag{3.5.17}\]

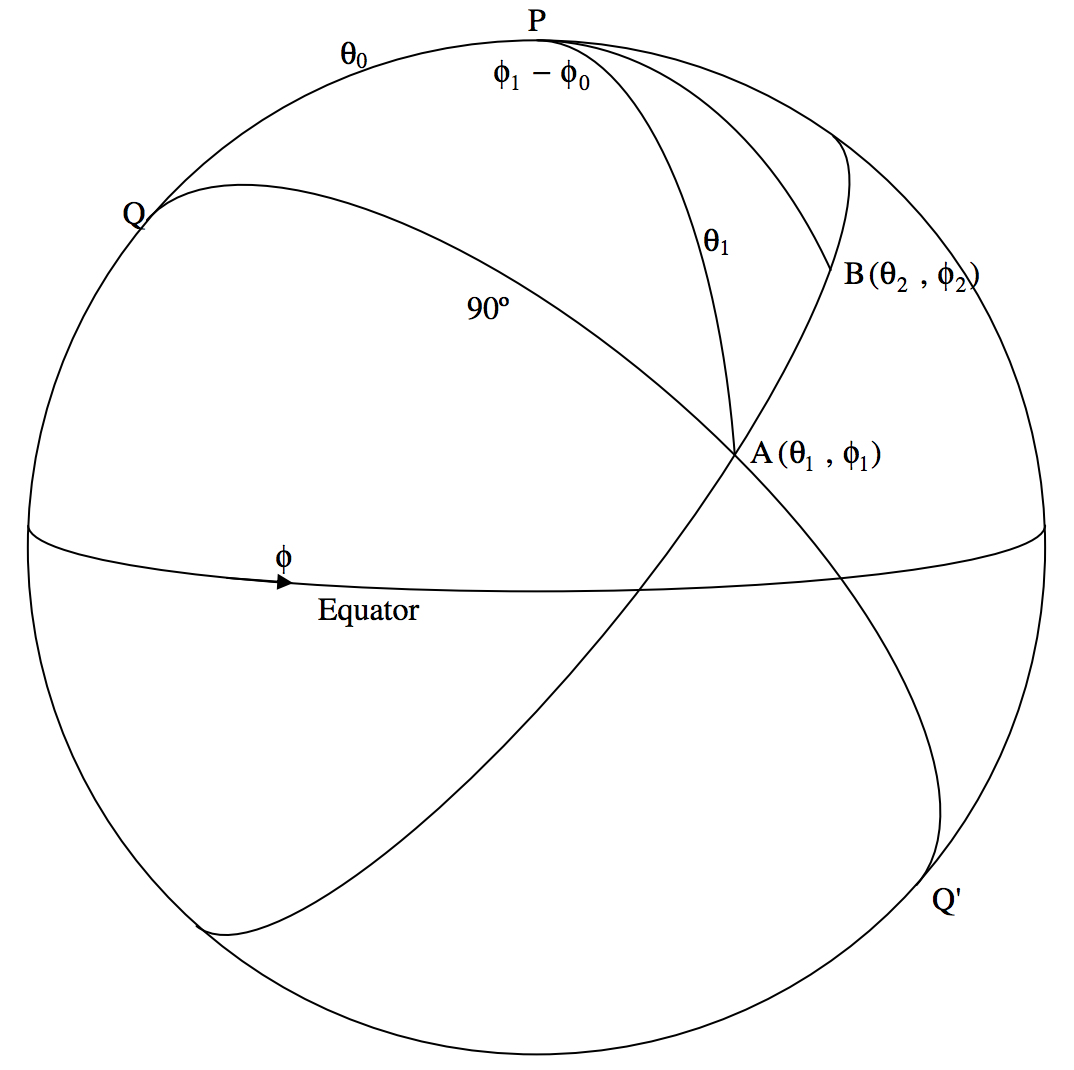
\(\text{FIGURE III.17}\)

Del mismo modo a partir del triángulo\(\text{PQB}\) obtendríamos

\[\tan θ_0 = -\frac{1}{\tan θ_2 \cos(\phi_2 - \phi_0)}. \label{3.5.18} \tag{3.5.18}\]

Estas son dos Ecuaciones en\(θ_0\) y\(\phi_0\), por lo que el problema está en principio resuelto. Equiparar los lados derechos de las dos Ecuaciones, ampliar los términos\(\cos (\phi_1 - \phi_0 )\) y\(\cos (\phi_2 - \phi_0 )\), reunir los términos en\(\sin \phi_0\) y\(\cos \phi_0\), eventualmente para obtener

\[\tan \phi_0 = \frac{\tan θ_1 \cos \phi_1 - \tan θ_2 \cos \phi_2}{\tan θ_2 \sin \phi_2 - \tan θ_1 \sin \phi_1}. \label{3.5.19} \tag{3.5.19}\]

Si sustituimos los ángulos dados en el problema original, obtenemos

\[\tan \phi_0 = \frac{\tan 70^\circ \cos 25^\circ - \tan 18^\circ \cos 44^\circ}{\tan 18^\circ \sin 44^\circ - \tan 70^\circ \sin 25^\circ} = -2.412 \ 091 \ 0\]

a partir de la cual\[\phi_0 = 112^\circ 31^\prime .1 \quad \text{or} \quad 292^\circ 31^\prime .1\]

Tenga en cuenta que obtenemos dos valores para\(\phi_0\) diferir por\(180^\circ\), como se esperaba.

Luego usamos cualquiera de las Ecuaciones\(\tan θ_0\) para obtener\(θ_0\) (Es una buena práctica usar ambas como verificación de la aritmética). La distancia polar norte, o colatitud, debe ser entre\(0^\circ\) y\(180^\circ\), por lo que no hay ambigüedad de cuadrante.

Con\(\phi_0 = 112^\circ 31^\prime .1\), obtenemos\(θ_0 = 96^\circ 47^\prime .1\), es decir latitud\(6^\circ 47^\prime .1 \ \text{S}\).
y con\(\phi_0 = 292^\circ 31^\prime .1\), obtenemos\(θ_0 = 83^\circ 12^\prime .9\), es decir latitud\(6^\circ 47^\prime .1 \ \text{N}\).

y estas son las coordenadas de los dos polos del gran círculo que pasan por\(\text{A}\) y\(\text{B}\). Se insta encarecidamente al lector a que realice estos cálculos numéricamente para estar bastante seguro de que los cuadrantes son correctos e inequívocos. En efecto, tratar el problema del cuadrante puede considerarse como la parte más importante del ejercicio.

Llegamos a Ecuación\(\ref{3.5.17}\) y\(\ref{3.5.18}\) resolviendo dos triángulos esféricos mediante los métodos de trigonometría esférica. El segundo método, sugerido, como se mencionó anteriormente, por Achintya Pal, utiliza los métodos de geometría de coordenadas algebraicas en tres dimensiones para llegar a las mismas Ecuaciones. Referimos coordenadas a ejes\(\text{O}xyz\). \(\text{O}\)es el centro de la Tierra, tomado como de radio unitario. \(\text{OP}\)es el\(z\) eje -. Los\(\text{O}y\) ejes\(\text{O}x\) y no están dibujados en la figura\(\text{III.17}\), sino que el\(x\) eje -se puede tomar para ser dirigido en algún lugar hacia la parte posterior del dibujo (lejos del lector), y el\(y\) -eje en algún lugar del frente del dibujo, estando ambos, por supuesto, en el plano del ecuador.

Escribamos la Ecuación al plano que contiene\(\text{A}\) y\(\text{B}\) en la forma

\[lx + my + nz = 0 \label{3.5.20} \tag{3.5.20}\]

Aquí\((l,m,n)\) están los cosenos de dirección de la normal al plano\(\text{AB}\), y están dados por

\[l = \sin θ_0 \cos \phi_0 \quad m = \sin θ_0 \sin \phi_0 \quad n = \cos θ_0 \label{3.5.21a,b,c} \tag{3.5.21a,b,c}\]

Las\((x,y,z)\) coordenadas del punto\(\text{A}\) son

\[x = \sin θ_1 \cos \phi_1 \quad y = \sin θ_1 \sin \phi_1 \quad x= \cos θ_1 \label{3.5.22a,b,c} \tag{3.5.22a,b,c}\]

En la sustitución de Ecuaciones\(\ref{3.5.21a,b,c}\) y\(\ref{3.5.22a,b,c}\) en Ecuación\(\ref{3.5.20}\) obtenemos:

\[\sin θ_0 \cos \phi_0 \sin θ_1 \cos \phi_1 + \sin θ_0 \sin \phi_0 \sin θ_1 \sin \phi_1 + \cos θ_0 \cos θ_1 = 0 \label{3.5.23} \tag{3.5.23}\]

Después de alguna manipulación algebraica muy modesta (por ejemplo, comenzar dividiendo por\(\sin θ_1 \cos θ_0\)) muy pronto llegamos de nuevo a la Ecuación\(\ref{3.5.17}\), y de manera similar a la Ecuación\(\ref{3.5.18}\).

Como bono, observamos que cualquier punto que tenga coordenadas esféricas que se\((θ, \phi)\) encuentran en el polo entero del gran círculo está en\(( θ_0 , \phi_0)\) satisface la Ecuación

\[\cot θ = - \tan θ_0 \cos (\phi - \phi) \label{3.5.24} \tag{3.5.24}\]

Esta Ecuación puede ser considerada como la\((θ, \phi)\) Ecuación al gran círculo\(\text{AB}\), y responde al problema contrario a la planteada originalmente: ¿Cuál es la Ecuación al gran círculo cuyo polo está en\((θ_0, \phi_0\))?

Ejemplo 3

Aquí hay un ejercicio desafiante y uno importante en astronomía de meteoritos. Se ven dos meteoros de lluvia, divergiendo de un radiante común. Uno inicia en la ascensión derecha 6 horas, declinación +65 grados, y termina en ascensión derecha 1 hora, declinación +75 grados. El segundo inicia a la ascensión derecha 5 h, declinación +35 grados, y termina en ascensión derecha 3 horas, declinación +15 grados. ¿Dónde está el radiante?

El estudiante asiduo hará un buen dibujo de la esfera celeste, ilustrando la situación con la mayor precisión posible. El cálculo requerirá alguna manipulación imaginativa de triángulos esféricos. Después de llegar a lo que crees que es la respuesta correcta, mira tu dibujo para ver si es razonable. El siguiente paso podría ser desarrollar una expresión trigonométrica general para la respuesta en términos de los datos originales, o programar el cálculo para una computadora, de manera que en adelante esté disponible para cualquier cálculo similar. O uno puede ir más allá, y escribir un programa de computadora que dará una solución de mínimos cuadrados para el radiante durante muchos más de dos meteoros en la ducha. Encuentro para la respuesta al problema anterior que el radiante está en ascensión recta 7.26 horas y declinación +43.8 grados.

Singularidad de las soluciones

El lector que por ahora ha trabajado a través de una variedad de problemas en la solución de un triángulo habrá notado que, dados tres elementos de un triángulo, a veces hay una solución única, mientras que a veces hay dos triángulos posibles que satisfacen los datos originales. Una vez más, a veces se puede encontrar que no existe una solución posible, es decir, que no existe un triángulo posible que satisfaga los datos dados, que por lo tanto debe presumirse incorrectos. Estoy muy en deuda con Alan Johnstone por las largas discusiones sobre este problema, y de hecho por señalar que algunas de las “soluciones” dadas en una versión anterior de estas notas eran de hecho inválidas (y ahora han sido corregidas). Creo que los siguientes criterios determinan cuántas soluciones válidas existen para un triplete dado de datos, para triángulos planos y para triángulos esféricos.

Se nos puede dar tres elementos de un triángulo,

Así

1. Tres lados:\(a, b, c,\)
2. Dos lados y el ángulo incluido:\(b, c, A.\)
3. Dos lados y un ángulo no incluido:\(a, b, A.\)
4. Dos ángulos y un lado común:\(a, B, C.\)
5. Dos ángulos y otro lado:\(A, B, a.\)
6. Tres ángulos:\(A, B, C.\)

Pregunta:

¿Cuál de estos da una solución única, y cuáles admiten dos soluciones? ¿Y cuáles son los triángulos imposibles? Creo que las respuestas son las siguientes:

\(\textbf{Plane Triangles}\)

i. Dejar\(d = a + b - c, \quad e = b + c - a, \quad f = c + a - b\)

Para un triángulo válido,\(d, \ e\) y todos\(f\) deben ser positivos. Si es así, existe una solución única.

ii. Hay una solución única.

iii. Si\(a>b\) hay una solución única.

Si\(a=b\), hay una solución única si\(A < 90^\circ\). De lo contrario no hay triángulo válido.

Si\(a < b\) hay cero, una o dos soluciones, según si

\(\sin A > \frac{a}{b}, \sin A = \frac{a}{b} \text{ or } \sin A < \frac{a}{b}\).

iv. Hay una solución única.

v. Hay una solución única.

vi. Existe una solución única excepto que solo se determinan las longitudes relativas de los lados.

\(\textbf{Spherical Triangles}\)

i. Dejar\(d = a + b - c, \quad e = b + c - a, \quad f = c + a - b\)

Para un triángulo válido,\(d, \ e\) y todos\(f\) deben ser positivos. Si es así, existe una solución única.)

ii. Hay una solución única.

iii. Si\(\sin A > \frac{\sin a}{\sin b}\), no hay una solución real.

Si\(A = a = b = 90^\circ\), entonces\(B = 90^\circ\), y\(c\) y\(C\) son iguales pero indeterminados.

De lo contrario:

Si\(a > b\) hay una solución única.

Si\(a = b\), hay una solución única si\(a < 90^\circ\). De lo contrario no hay una solución real.

Si\(a < b\) hay una o dos soluciones, según si

\[\sin A = \frac{\sin a}{\sin b} \text{ or } \sin A < \frac{\sin a}{\sin b}.\]

iv. Hay una solución única.

v. Si\(\sin A = \frac{\sin A }{\sin B}\), no hay una solución real.

Si\(A=B=a=90^\circ\), entonces\(b = 90^\circ\), y\(c\) y\(C\) son iguales pero indeterminados.

De lo contrario:

Si\(A>B\) hay una solución única.

Si\(A=B\), hay una solución única si\(a<90^\circ\). De lo contrario no hay una solución real.

Si\(A<B\) hay una o dos soluciones, según si

\[\sin a = \frac{\sin A}{\sin B} \text{ or } \sin a < \frac{\sin A}{\sin B}.\]