3.6: Rotación de Ejes, Dos Dimensiones

Última actualización
Guardar como PDF

Page ID: 131032

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

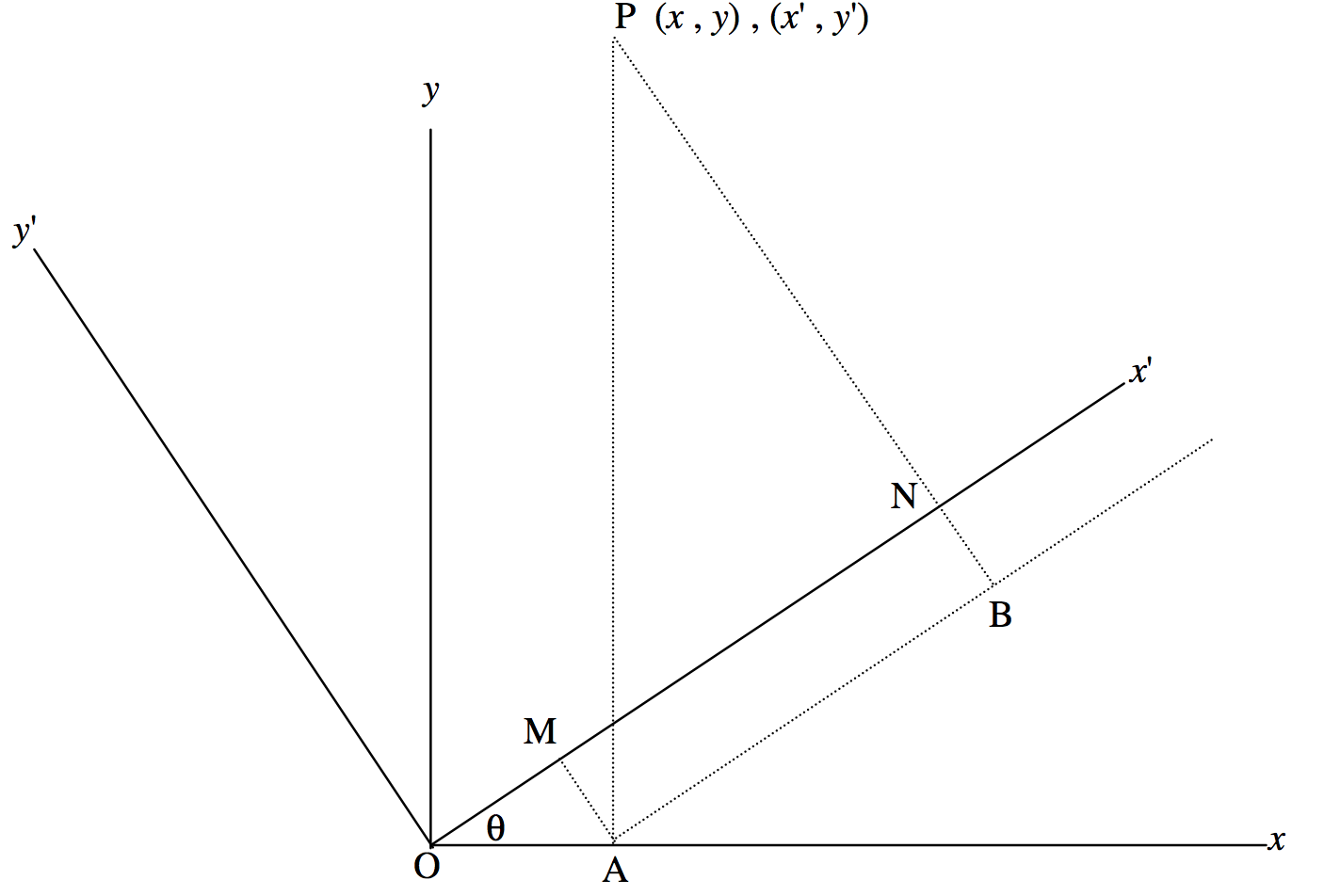
En esta sección consideramos el siguiente problema. Considere dos conjuntos de ejes ortogonales\(\text{O}x, \text{O}y\),\(\text{O}x^\prime, \text{O}y^\prime\), y, tal que un conjunto forme un ángulo\(θ\) con respecto al otro. Véase la figura a continuación. \(\text{A}\)punto\(\text{P}\) puede describirse ya sea por sus coordenadas\((x,y)\) con respecto a un “conjunto de bases”\(\text{O}x, \text{O}y\), o por sus coordenadas con respecto al otro conjunto de bases\(\text{O}x^\prime, \text{O}y^\prime\). La pregunta es, ¿cuál es la relación entre las coordenadas\((x,y)\) y las coordenadas\((x^\prime,y^\prime)\)? Ver figura\(\text{III.18}\).

Vemos que\(\text{OA} = x, \ \text{AP} = y, \ \text{ON} = x^\prime, \ \text{PN} = y^\prime, \ \text{OM} = x \cos θ, \ \text{MN} = y \sin θ\),

\[\therefore \quad x^\prime = x \cos θ + y \sin θ. \label{3.6.1} \tag{3.6.1}\]

También\(\text{MA} = \text{NB} = x \sin θ, \quad \text{PB} = y \cos θ,\)

\[\therefore \quad y^\prime = -x \sin θ + y \cos θ. \label{3.6.2} \tag{3.6.2}\]

Estas dos relaciones se pueden escribir en forma de matriz como

\[\pmatrix{x^\prime \\ y^\prime} = \pmatrix{\cos θ & \sin θ \\ -\sin θ & \cos θ} \pmatrix{x \\ y}. \label{3.6.3} \tag{3.6.3}\]

Figura 3.18.png
\(\text{FIGURE III.18}\)

Existen varias formas de obtener las relaciones conversas; es decir, Ecuaciones para\(x\) y\(y\) en términos de\(x^\prime\) y\(y^\prime\). Una manera sería diseñar dibujos similares a (b) y (c) que muestren claramente las relaciones contrarias, y se alienta al lector a hacerlo. Otra forma es simplemente resolver las dos Ecuaciones anteriores (que pueden considerarse como dos Ecuaciones simultáneas en\(x\) y\(y\)) para\(x\) y\(y\). Menos tedioso es intercambiar los símbolos cebados y no cebados y cambiar el signo de\(θ\). Quizás el más rápido de todos es reconocer que el determinante de la matriz

\[\pmatrix{\cos θ & \sin θ \\ -\sin θ & \cos θ}\]

es unidad y por lo tanto la matriz es una matriz ortogonal. Una propiedad importante de una matriz ortogonal M es que su recíproco M\(^{−1}\) es igual a su transposición\(\tilde{\textbf{M}}\) (formada por la transposición de las filas y columnas). Por lo tanto, la relación inversa que buscamos es

\[\pmatrix{x \\ y} = \pmatrix{\cos θ & \sin θ \\ - \sin θ & \cos θ}^{-1} \pmatrix{x^\prime \\ y^\prime} = \pmatrix{\cos θ & -\sin θ \\ \sin θ & \cos θ} \pmatrix{x^\prime \\ y^\prime}. \label{3.6.4} \tag{3.6.4}\]

Al lector le gustaría probar los cuatro métodos para asegurarse de que todos lleguen al mismo resultado.