8.4: Movimiento Directo y Retrógrado, y Puntos Estacionarios
- Page ID
- 130996
Como se ve desde el polo eclíptico norte, los planetas principales se mueven en sentido antihorario alrededor del Sol. Tal movimiento se llama movimiento directo o progrado. Se dice que un cuerpo que se mueve en sentido horario (como algunos cometas) se mueve retrógrado.
En figura\(\text{VIII.4}\) he dibujado la Tierra moviéndose alrededor del Sol a velocidad angular\(ω_0\) y un planeta superior (que he indicado en oposición y en conjunción) moviéndose con velocidad angular más lenta\(ω\).
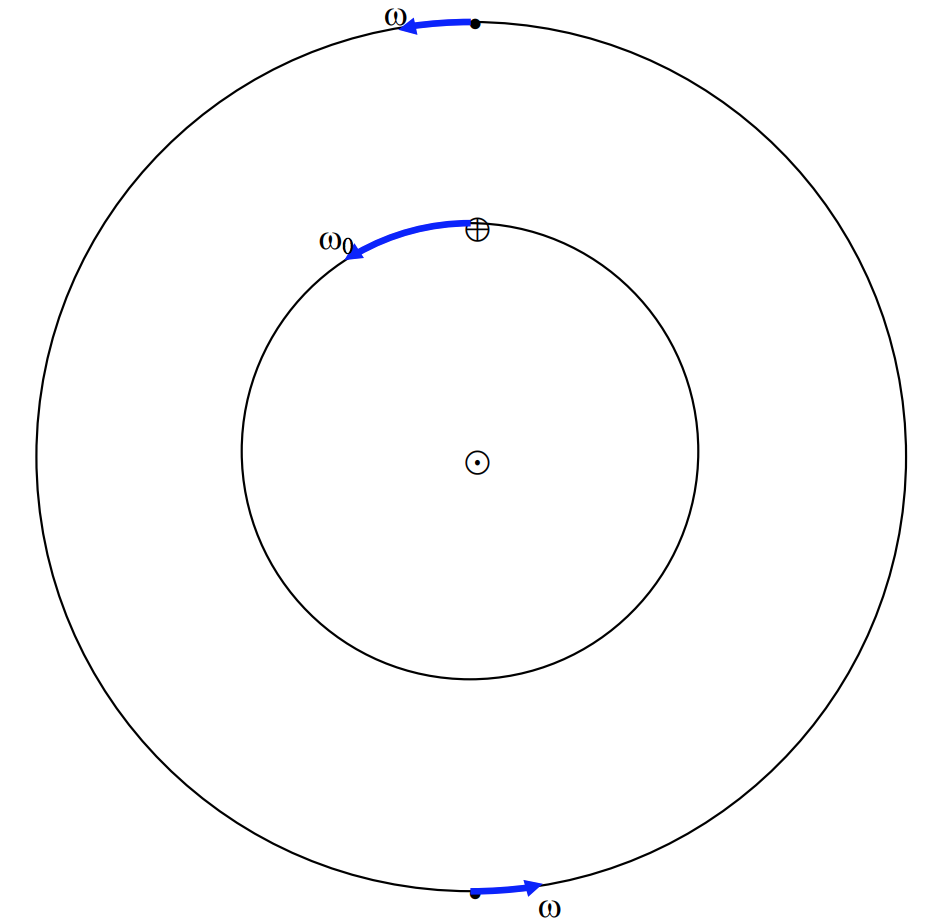
\(\text{FIGURE VIII.4}\)
En la figura\(\text{VIII.5}\). He dibujado la misma situación pero me he referido a lo que llamo un marco de referencia sinódico. Es decir, un marco de referencia que está co-rotando con la Tierra, tal que la línea Tierra-Sol es estacionaria. En el marco sinódico, el planeta se mueve en sentido horario a velocidad angular\(ω − ω_0\).
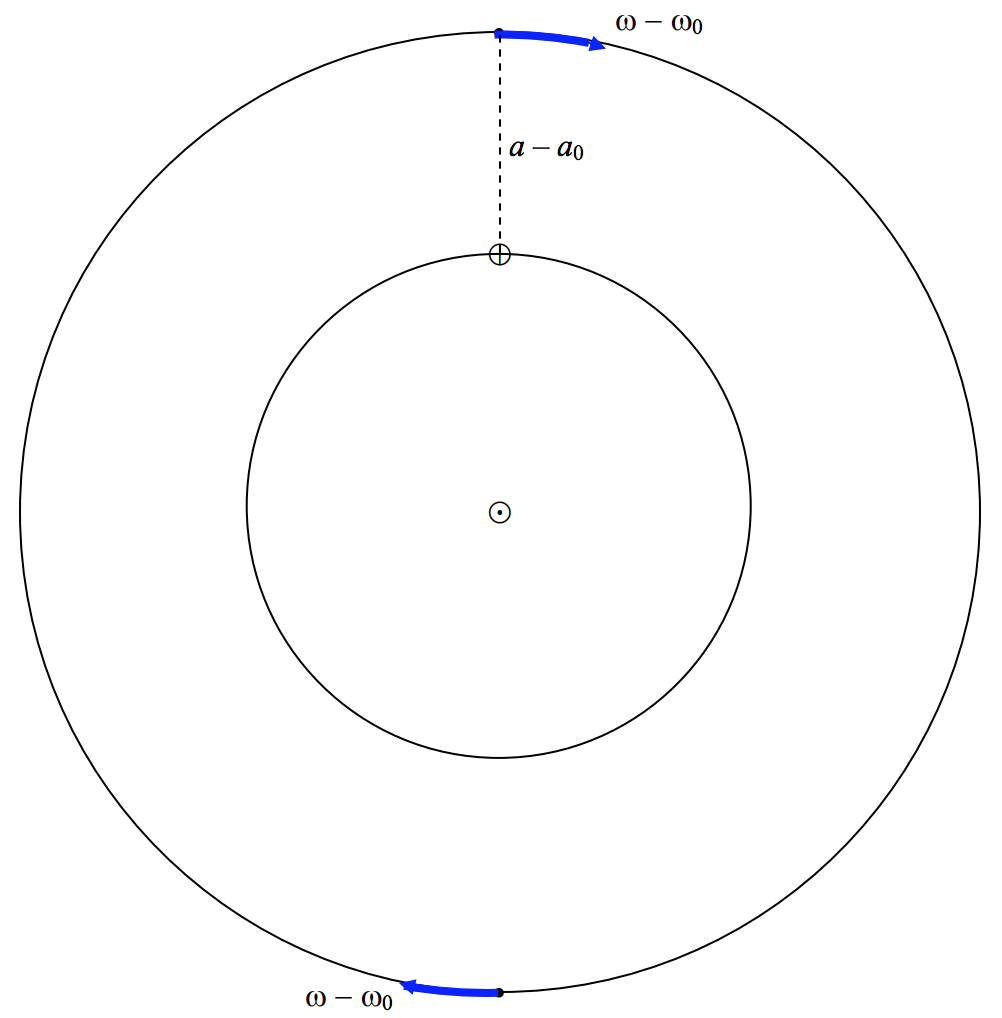
\(\text{FIGURE VIII.5}\)
Dejemos\(a_0\) y\(a\) sean los radios o la órbita de la Tierra y del planeta respectivamente. En ese caso, la velocidad angular del planeta en el marco sideral es, por tercera ley de Kepler, en\(ω = ω_0 \left( \frac{a_0}{a} \right)^{3/2}\) sentido antihorario, y por tanto, en el marco sinódico, es en\(ω_0 \left[ 1 - \left( \frac{a_0}{a} \right)^{3/2} \right]\) sentido horario. A partir de este punto, voy a expresar velocidades angulares en unidades de\(ω_0\) y distancias en unidades astronómicas (\(a_0 = 1\)). En estas unidades, entonces, la velocidad angular del planeta alrededor del Sol en el marco sinódico es en el sentido de\(1 – a^{−3/2}\) las agujas del reloj, y su velocidad lineal en su órbita (de radio\(a\)) es\(a(1 – a^{−3/2})\).
Ahora supongamos que el planeta está en oposición, de manera que su distancia de la Tierra está\(a – 1\). La velocidad angular del planeta vista desde la Tierra es, por lo tanto, en\(\frac{a ( - a^{-3/2})}{a-1}\) sentido horario. Para planetas y asteroides superiores (\(a > 1\)), esto va de\(1.5\) a\(1.0\) como\(a\) va de\(1\) a\(∞\). Ahora en el marco sinódico, la esfera celeste con las estrellas fijas sobre ella gira alrededor de la Tierra a velocidad angular\(1\). Por lo tanto, en oposición, la velocidad angular del planeta contra el fondo de las estrellas (también conocida como el aparente movimiento propio, para lo cual utilizaré el símbolo\(p\)) del planeta es la expresión anterior menos\(1\), que, después de la simplificación, se convierte en
\[p = \frac{1 - 1/\sqrt{a}}{a-1} \label{8.4.1} \tag{8.4.1}\]
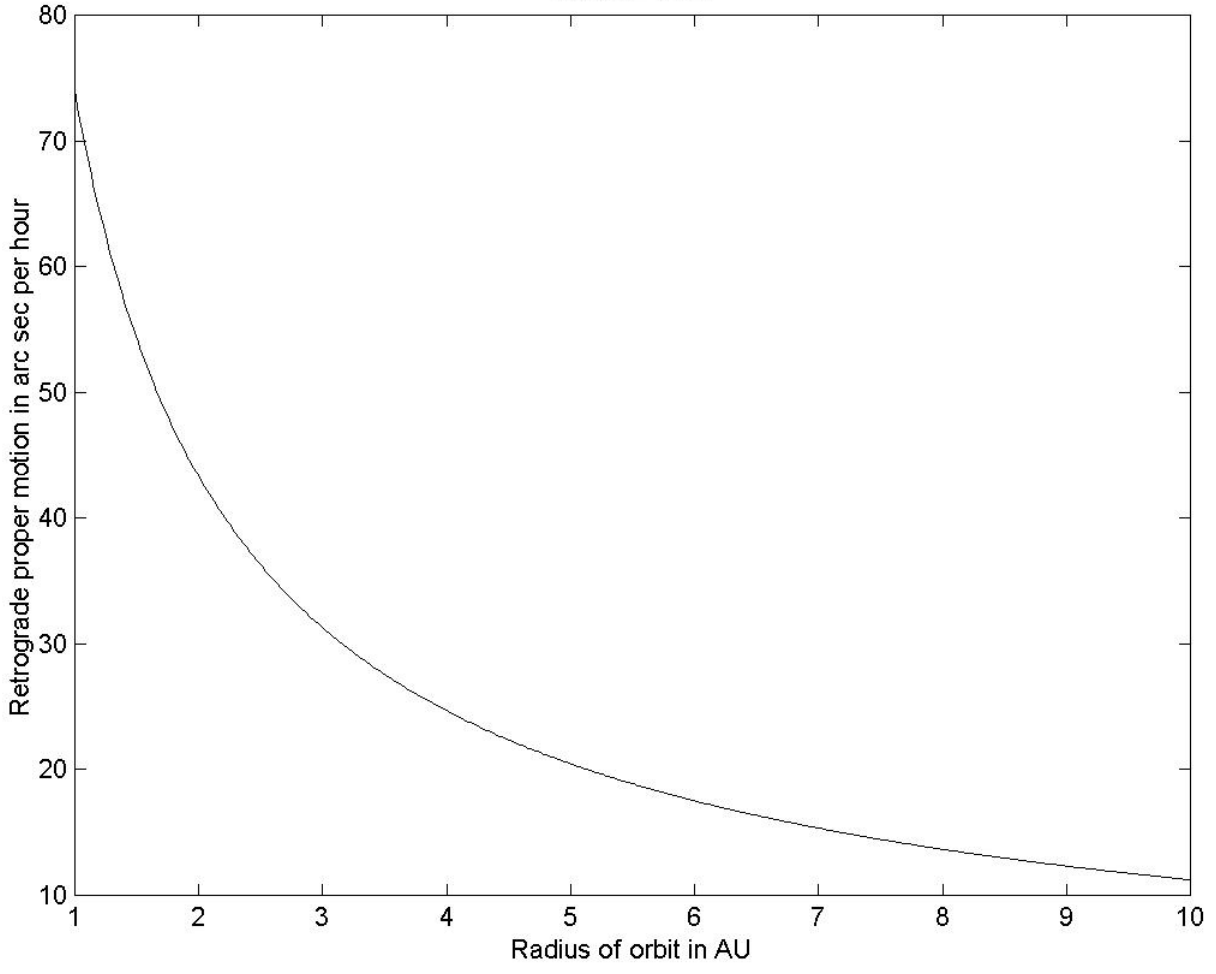
en la dirección de disminuir la longitud eclíptica o disminuir la ascensión derecha, es decir, hacia el oeste. Es decir, a la oposición, el planeta aparece desde la Tierra para estar moviéndose en dirección retrógrada. Se recuerda al lector que, en la Ecuación\ ref {8.4.1},\(p\) es el movimiento adecuado hacia el oeste, en unidades de\(ω_0 = 147.8\) segundos de arco por hora solar media, y\(a\) es el radio de la órbita del planeta en\(\text{AU}\). En la figura\(a\) se muestra una gráfica de\(p\) versus\(\text{VIII.6}\).
La ecuación\ ref {8.4.1} nos permite calcular\(p\) dado\(a\). El problema más interesante es calcular\(a\) dado\(p\). Así, estás buscando asteroides cerca del punto de oposición una noche, y un nuevo planeta nada en tu ken. (Eso es de un poema de Keats, por cierto.) Se ve que se está moviendo retrógrada con respecto a las estrellas por tantos segundos de arco por hora. Suponiendo que se está moviendo en órbita circular, ¿cuál es el radio de su órbita? La respuesta rápida, por supuesto, es mirar la figura\(\text{VIII.6}\), pero también puedes mantener tu mano en el álgebra de secundaria invirtiendo la ecuación\ ref {8.4.1} para obtener
\[a = \frac{p+2 - \sqrt{p(p+4)}}{2p}. \label{8.4.2} \tag{8.4.2}\]
Consideraciones similares para un planeta inferior demostrarán que, en conjunción inferior, es la velocidad angular del planeta hacia el oeste\(\frac{a(a^{-3/2} - 1)}{1-a}\), que es la misma que la fórmula para un planeta superior en oposición. Como\(a\) va de\(1\) a\(0\), esto va de\(1.5\) a\(∞\). En el marco sinódico, las estrellas se mueven hacia el oeste a velocidad angular\(1\), por lo que, en relación con las estrellas de fondo, un planeta inferior en conjunción inferior tiene un movimiento propio retrógrado (hacia el oeste) dado por la misma fórmula que para un planeta superior en conjunción superior, a saber, Ecuación\ ref {8.4.1}. Una gráfica de\(p\) versus\(a\) para un planeta inferior cae de\(∞\)\(a = 0\) a\(73.9\) arcsec por hora a\(a = 1\). Sólo para mantener pulidas tus habilidades álgebra, puedes demostrar desde la Ecuación\ ref {8.4.1} que cuando\(a = 1\),\(p = ½\).
\(\text{FIGURE VIII.6}\)
Así, un planeta superior en oposición se mueve hacia el oeste (“retrograda”) en relación con las estrellas, y un planeta inferior en conjunción inferior también se mueve hacia el oeste (“retrograda”) en relación con las estrellas.
Sin embargo, será obvio que un planeta superior en conjunción, o un planeta inferior en conjunción superior, se moverá hacia el este (“directo” o “prógrado”) en relación con las estrellas. Por lo tanto, en algún momento de su órbita un planeta estará estacionario en relación con las estrellas en el momento en que su movimiento adecuado cambie de directo a retrógrado. Como se ve desde la Tierra, un planeta se mueve generalmente hacia el este en relación con las estrellas, excepto por un corto tiempo cerca de la oposición (para un planeta superior) o conjunción inferior (para un planeta inferior) cuando retrograda brevemente hacia el oeste. No es de extrañar que los antiguos astrónomos, creyendo que la Tierra estaba en el centro del sistema solar, creyeran en su sistema de deferentes y epiciclos. Hoy creeríamos lo mismo si no hubiéramos leído de manera diferente en los libros y en este sitio web.
Dos pequeñas palabras de precaución. A veces se cree por los incautos que los puntos estacionarios en la órbita de un planeta inferior ocurren cuando el planeta está en mayor elongación del Sol. No es así, y efectivamente hay un pequeño ejercicio sobre este punto en el penúltimo párrafo de este capítulo. El segundo pequeño punto a notar es que, para un trabajo preciso, es necesario distinguir entre cuando un planeta está estacionario (es decir, está en el momento de cambiar de dirección) en ascensión derecha, y cuándo está estacionario en longitud eclíptica. En nuestro sencillo modelo de órbitas coplanares, no necesitamos hacer esta distinción fina.
En lo que sigue, vamos a calcular (para nuestro modelo coplanario circular concéntrico) la distancia angular de un planeta superior desde el punto de oposición cuando está estacionario, y la distancia angular (“elongación”) del Sol cuando un planeta inferior está estacionario. Empezaremos con un planeta superior.
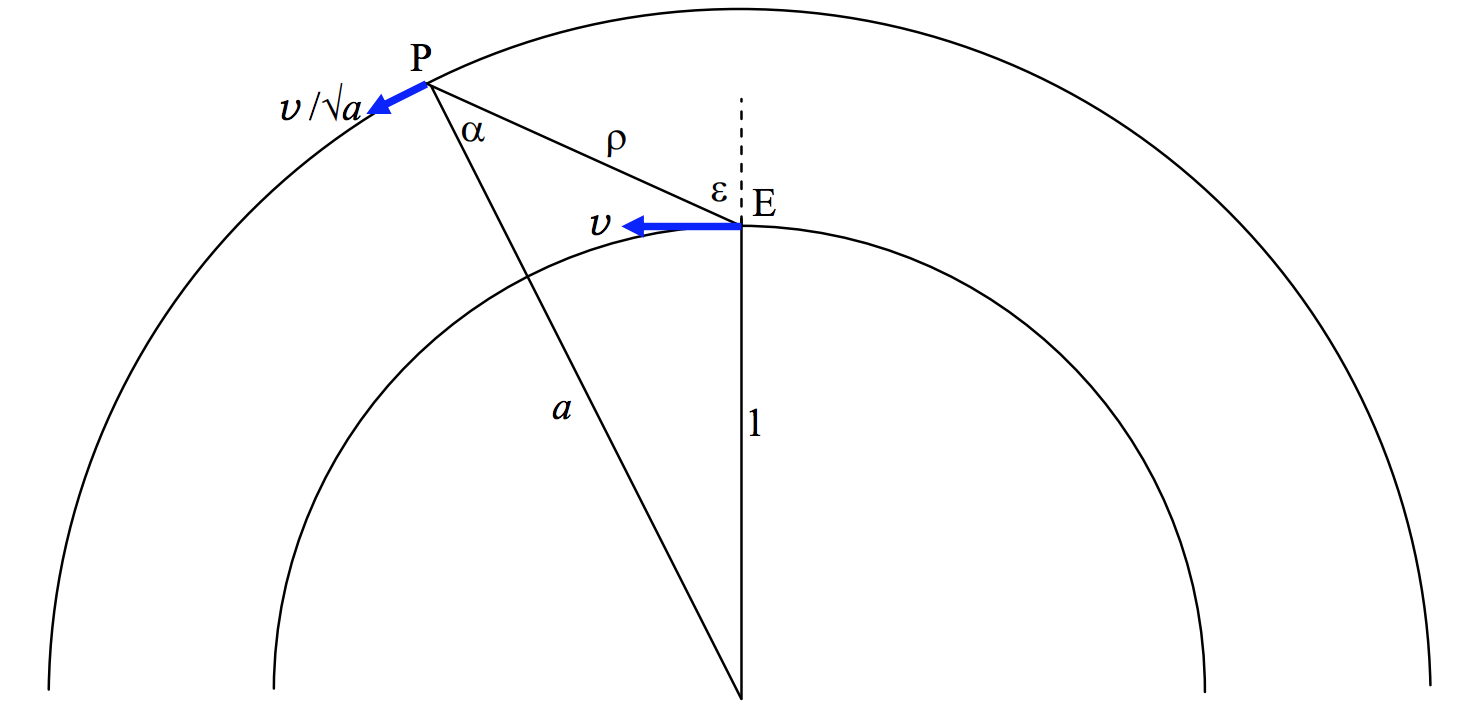
\(\text{FIGURE VIII.7}\)
La figura\(\text{VIII.7}\) muestra la Tierra\(\text{E}\) moviéndose en su órbita de radio\(1 \ \text{AU}\) con velocidad\(v\), y un planeta o asteroide superior\(\text{P}\) moviéndose en su órbita de radio\(a \ \text{AU}\) con velocidad\(v /√a\). El ángulo\(ε\) es la distancia angular del planeta desde el punto de oposición. El ángulo\(α\) se conoce como ángulo de fase. No hay movimiento aparente del planeta contra el fondo estrellado (es decir, el planeta está en su punto estacionario) cuando los componentes de los dos vectores de velocidad perpendiculares a la línea\(\text{EP}\) son iguales. Es decir, el planeta está en un punto estacionario cuando\( \frac{v}{\sqrt{a}} \cosα = v \cos ε\), o
\[\cos α = \sqrt{a} \cos ε. \label{8.4.3} \tag{8.4.3}\]
Pero desde el triángulo\(\text{SEP}\) tenemos
\[a \sin α = \sin ε . \label{8.4.4} \tag{8.4.4}\]
Al eliminar\(α\) de las ecuaciones\ ref {8.4.3} y\ ref {8.4.4}, encontramos que el planeta se encuentra en un punto estacionario cuando su distancia angular desde el punto de oposición viene dada por
\[\tan ε = \frac{a}{\sqrt{1+a}}. \label{8.4.5} \tag{8.4.5}\]
Sobre la inversión de esta Ecuación (¡hazlo!) , encontramos que la distancia heliocéntrica de un planeta que llega a su punto estacionario a una distancia angular\(ε\) del punto de oposición es
\[a = \frac{1}{2} \left( t + \sqrt{t(t+4)} \right) , \label{8.4.6} \tag{8.4.6}\]
donde\(t = \tan^2 ε\).
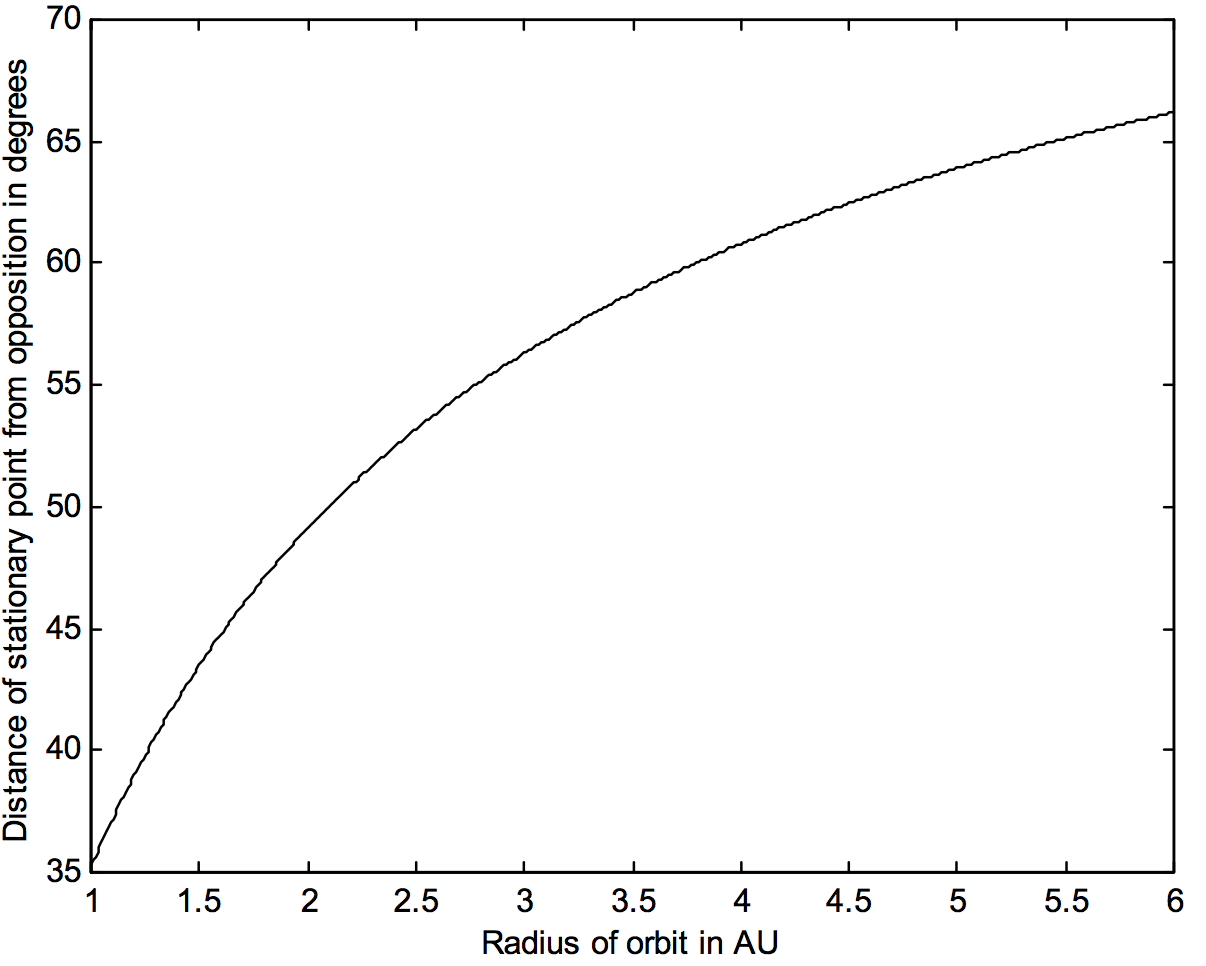
La relación entre\(a\) y\(ε\) se muestra en la figura\(\text{VIII.8}\). La menor distancia angular posible del punto estacionario desde la oposición para un planeta superior que se mueve en órbita circular es\(\tan^{−1} 1/(√2) = 35^\circ \ 16^\prime = 02^\text{h} \ 21^\text{m}\).
\(\text{FIGURE VIII.8}\)
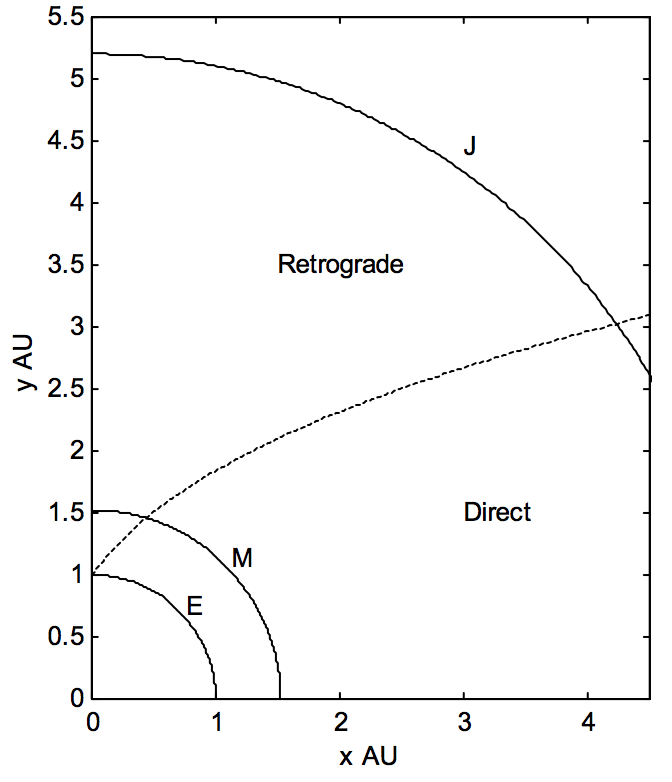
Figura\(\text{VIII.9}\), en la que el Sol está en su origen, muestra las órbitas de la Tierra, Marte y Júpiter, y divide la zona en la que los asteroides que se mueven en órbitas circulares tendrán movimientos propios directos o retrógrados.
\(\text{FIGURE VIII.9}\)
Si el lector realiza el mismo análisis para planetas inferiores, encontrará que las Ecuaciones\(\ref{8.4.4}\) se\(\ref{8.4.6}\) aplican igualmente bien, excepto que, en el caso de planetas inferiores (y asteroides inferiores, como el grupo Aten, de los cuales es probable que se descubran más en los próximos años) el ángulo \(ε\)es la distancia angular o elongación del planeta desde el Sol más que desde el punto de oposición, y\(35^\circ 16^\prime\) es el mayor valor que esto pueda tener para el punto estacionario de un planeta inferior en una órbita circular. La Ecuación correspondiente a\(\ref{8.4.3}\) se convierte, pues en planeta inferior,\(\cos α = − \sqrt{a} \cos ε\). El alargamiento del punto estacionario es, como era de esperar, menor que el mayor alargamiento. También, para un planeta inferior, cabe señalar que, para un alargamiento dado (distinto al alargamiento mayor) son posibles dos ángulos de fase y son posibles dos distancias geocéntricas. En el punto estacionario, el ángulo de fase obtuso y la menor de las dos distancias geocéntricas son las correctas.
Por supuesto, en general, no es probable que estemos observando un asteroide exactamente en el punto de oposición o exactamente en un punto estacionario. Ahora abordamos el problema un poco más difícil: ¿Cuál es el movimiento adecuado de un asteroide cuyo radio orbital circular es\(a\) cuando se observa a una\(ε\) distancia angular del punto de oposición (o del Sol)? O, a la inversa, si observamos un asteroide a una\(ε\) distancia angular del punto de oposición, y vemos que tiene un movimiento adecuado\(p\), ¿cuál es el radio de su órbita (supuesta circular)?
En la figura 9b vemos, en un marco de referencia sideral, las órbitas de la Tierra\(\text{E}\),, y un planeta superior (o asteroide)\(\text{P}\), siendo\(1\) y los radios de sus órbitas\(a \ \text{AU}\). Las distancias heliocéntricas y geocéntricas del planeta son\(a\) y\(ρ\). La distancia angular del planeta desde el punto de oposición es\(ε\) y el ángulo de fase es\(α\). La Tierra se mueve con velocidad angular 1 (en unidades de\(ω_0\)) y el planeta se mueve (según la tercera ley de Kepler) con velocidad angular\(a^{−3/2}\).
En la figura 9c vemos la misma situación en un marco de referencia sinódico, en el que la Tierra está estacionaria y el planeta se mueve en sentido horario a una velocidad angular\(1 − a^{−3/2}\) (en unidades de\(ω_0\)).
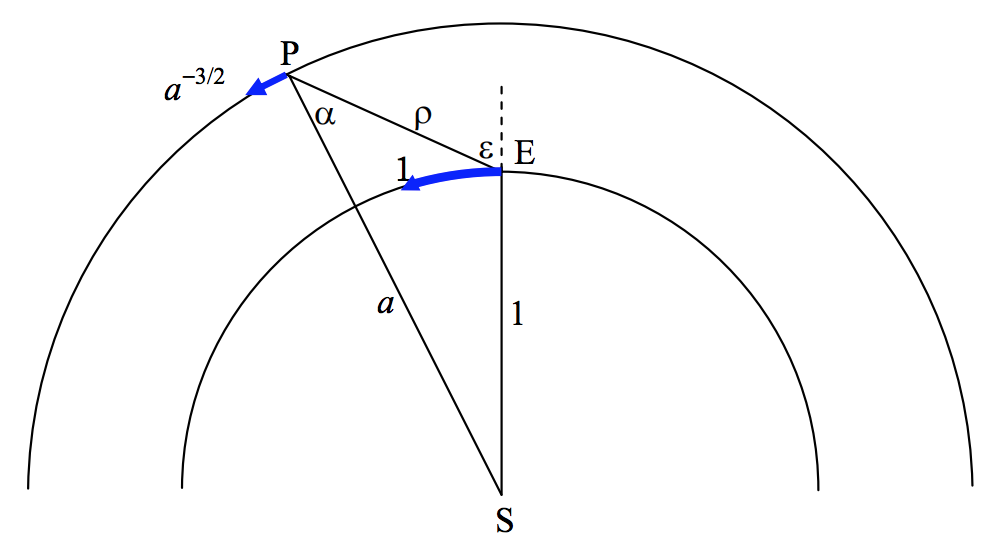
\(\text{FIGURE VIII.9B}\)
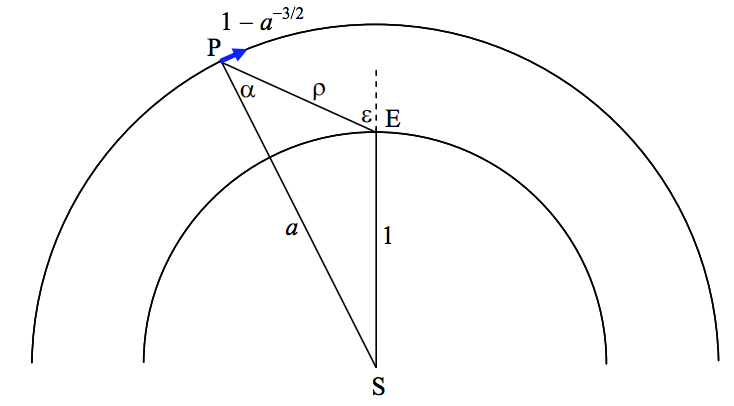
\(\text{FIGURE VIII.9C}\)
En el marco sinódico, la velocidad lineal del planeta (cuya velocidad angular es\(1 − a^{−3/2}\) y cuya distancia heliocéntrica es\(a\)) es
\[a(1 - a^{-3/2} ) = a - \frac{1}{\sqrt{a}}. \label{8.4.7} \tag{8.4.7}\]
El componente transversal de esta velocidad visto desde la Tierra es
\[\left( a - \frac{1}{\sqrt{a}} \right) \cos α, \label{8.4.8} \tag{8.4.8}\]
para que su velocidad angular vista desde la Tierra sea
\[\frac{1}{ρ} \left( a - \frac{1}{\sqrt{a}} \right) \cos α \label{8.4.9} \tag{8.4.9}\]
retrógrada.
En el marco sinódico, las estrellas se mueven retrógradas a velocidad angular\(1\). Por lo tanto, el planeta se mueve directamente en relación con las estrellas de fondo a velocidad angular
\[p = 1 - \frac{1}{ρ} \left( a - \frac{1}{\sqrt{a}} \right) \cos α \label{8.4.10} \tag{8.4.10}\]
y este es el movimiento adecuado requerido. En esta Ecuación, la geometría muestra que
\[a \sin α = \sin ε \label{8.4.11} \tag{8.4.11}\]
y\[ρ^2 = 1 + a[a - 2 \cos (ε - α) ] . \label{8.4.12} \tag{8.4.12}\]
Así se\(p\) puede calcular, dado\(ε\) y\(a\).
El problema más interesante y práctico, sin embargo, es que se ha observado un asteroide a una\(ε\) distancia angular del punto de oposición, y se está moviendo a una velocidad angular\(p\) relativa al fondo estrellado. (Contaremos\(p\) como positivo si el movimiento adecuado es directo, es decir, si el asteroide se mueve hacia el este en relación con las estrellas. El signo de\(ε\) no importa.) Vas a tener que invertir la Ecuación\ ref {8.4.10}. No estoy seguro si esto se puede hacer fácilmente algebraicamente, así que tu reto es escribir un programa de computadora que devuelva un dato dado numéricamente\(p\) y\(ε\) como datos de entrada. Se puede hacer, pero no voy a fingir que es fácil.
Cuando hayas hecho esto, aquí tienes tres ejemplos para ti:
1. Movimiento apropiado = 40 segundos de arco por hora hacia el oeste; es decir,\(p = −40\) arcsec por hora. \(ε = 20^\circ\). Encuentra la distancia heliocéntrica\(a\) en\(\text{AU}\).
2. \(p = +40"/\text{hr}. \ ε = 70^\circ\). Encuentra\(a\).
3. \(p = −15"/\text{hr}. \ ε = 40^\circ\). Encuentra\(a\).
He escrito mi propio programa Fortran para invertir Ecuación\(\ref{8.4.10}\), usando la iteración de Newton-Raphson, y aquí están las respuestas que me da.
1. \(a = 1.578 \ \text{AU}\)
2. \(a = 1.718 \ \text{AU}\)
3. ¡Mensaje de error!
¡Mi computadora no pudo hacer el ejemplo número 3! En otras palabras, dado un movimiento adecuado de\(−15"/\text{hr}\) y una distancia de oposición de\(40^\circ\), ¡no me podía decir la distancia heliocéntrica!
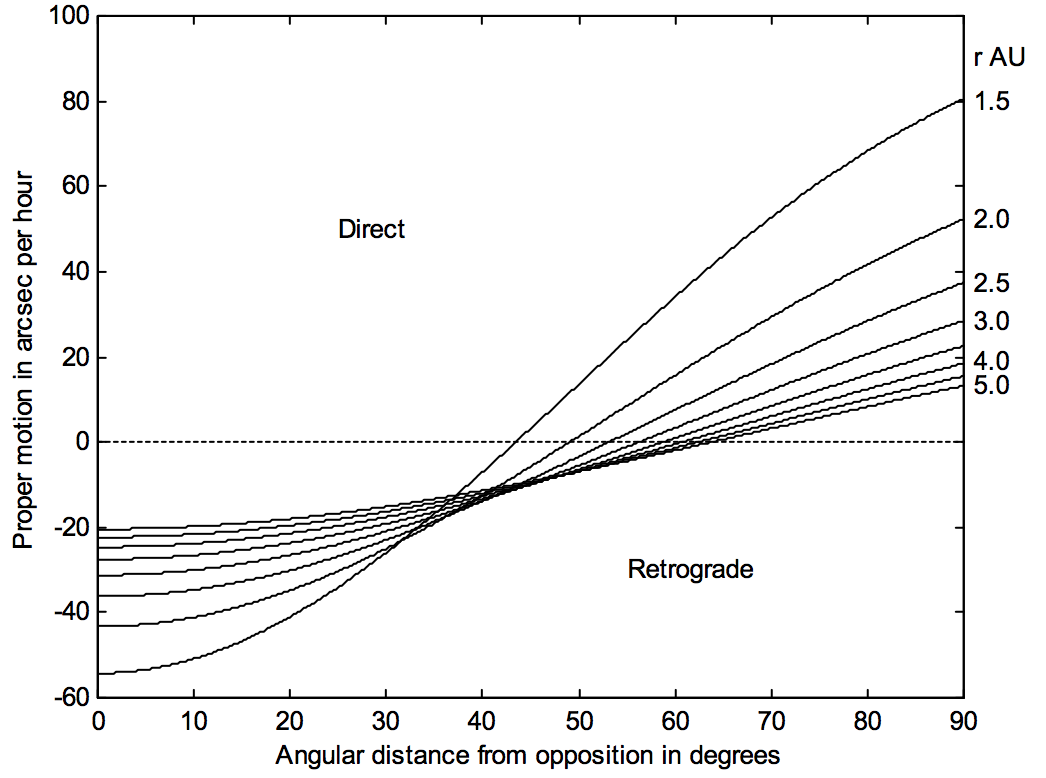
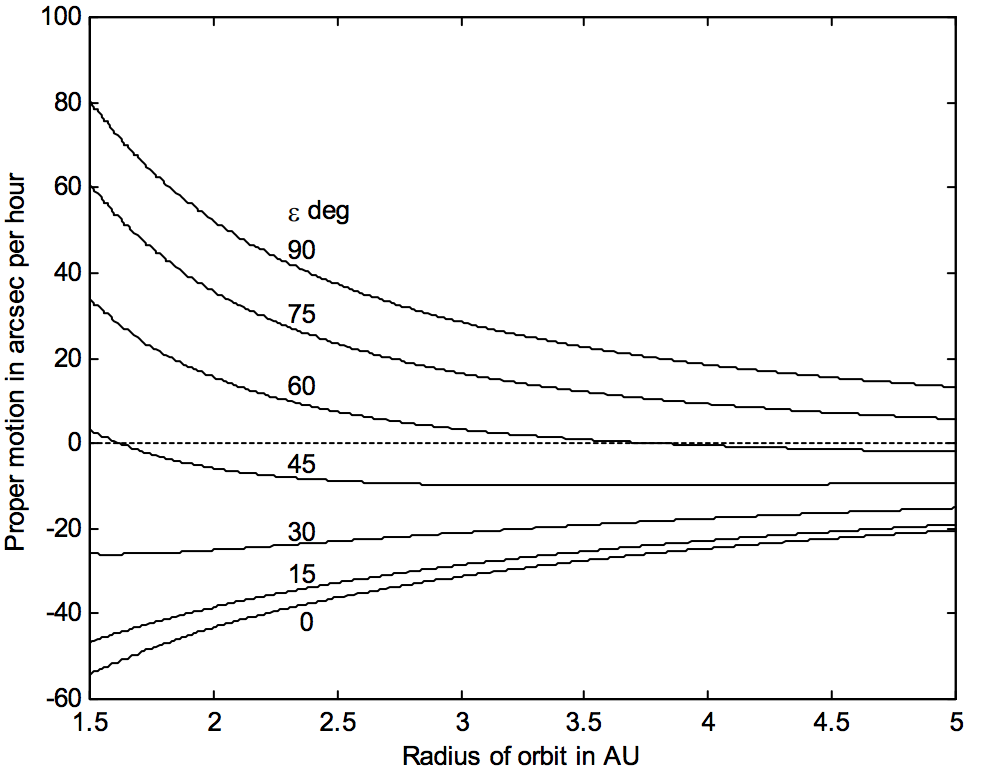
En la figura\(\text{VIII.10}\) he trazado el movimiento apropiado versus\(ε\) para varias distancias heliocéntricas, y en la figura\(\text{VIII.11}\) he dibujado el movimiento apropiado versus la distancia heliocéntrica para varias\(ε\). Encontrarás que puedes encontrar fácilmente soluciones aproximadas a los dos primeros de estos problemas desde cualquiera de las figuras, pero no puedes resolver el tercer problema desde ninguna de las figuras. En otras palabras, dadas ciertas combinaciones de\(p\) y\(ε\), simplemente no es posible determinar\(a\). Hay un amplio rango de valor de\(a\) y\(ε\) que dan como resultado el mismo movimiento adecuado.
Si realizas el mismo análisis para planetas inferiores, encontrarás que las Ecuaciones que corresponden a las Ecuaciones 8,4,10-12 son las siguientes:
\[p = 1 + \frac{1}{ρ} \left( \frac{1}{\sqrt{a}} - a \right) \cos α . \label{8.4.13} \tag{8.4.13}\]
Esto es lo mismo que la Ecuación\ ref {8.4.10}.
\[a \sin α = \sin ε . \label{8.4.14} \tag{8.4.14}\]
Esto es lo mismo que la Ecuación\ ref {8.4.11}, salvo que, para un planeta inferior,\(ε\) es el alargamiento del Sol y hay dos soluciones para\(α\), una aguda y la otra obtusa. Como anunció Galileo: Cynthiae figuras aemulatur mater amorum.
La Ecuación que corresponde a la Ecuación\ ref {8.4.12} es
\[ρ^2 = 1 + a [ a + 2 \cos (ε + α) ] , \label{8.4.15} \tag{8.4.15}\]
que difiere ligeramente de la ecuación\ ref {8.4.12}
\(\text{FIGURE VIII.10}\)
\(\text{FIGURE VIII.11}\)
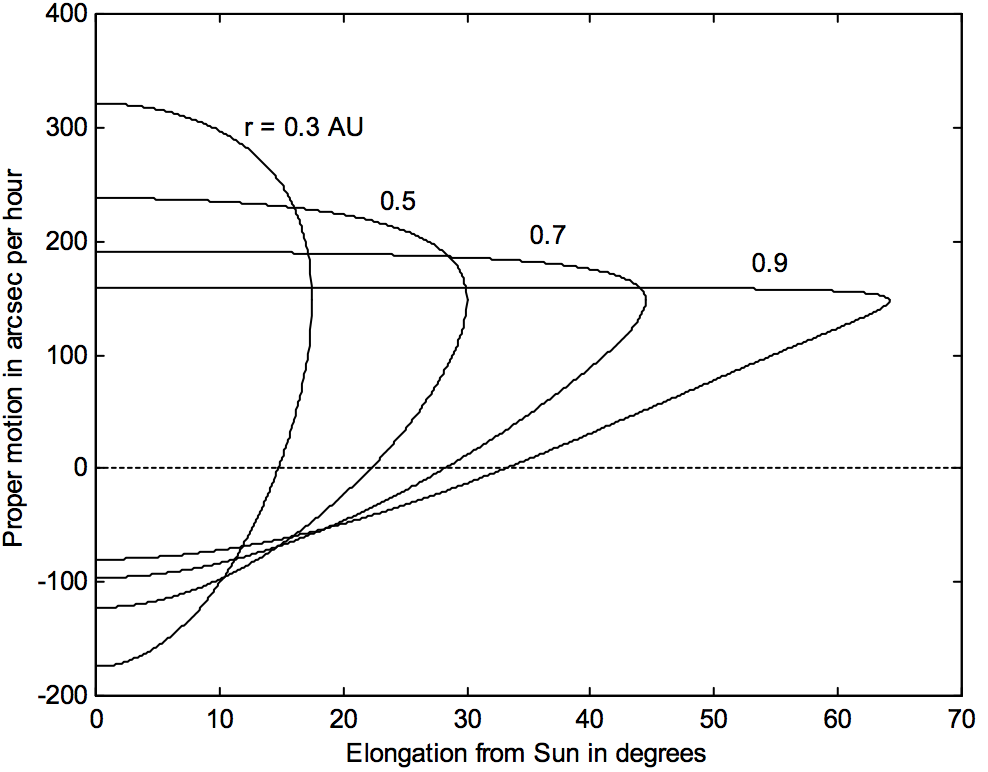
En la figura\(\text{VIII.12}\) he trazado el movimiento adecuado versus elongación del Sol para varias distancias heliocéntricas inferiores. Observará que, para un alargamiento dado y movimiento adecuado, hay dos posibles soluciones para\(a\), y no hay nada que pueda hacer al respecto a partir de una sola observación de\(ε\) y\(p\). Porque\(ε = 0\) (conjunción con el Sol), el movimiento adecuado es positivo en conjunción superior y negativo en conjunción inferior.
\(\text{FIGURE VIII.12}\)
Como ejercicio, tal vez quieras convencerte —ya sea a partir de las Ecuaciones o simplemente de la geometría de la situación— de que el movimiento adecuado relativo a las estrellas de cualquier planeta inferior en una órbita circular con mayor elongación es independiente del radio de la órbita. ¿Cuál es este movimiento adecuado en arcsec por hora?
Resumen. Las gráficas y ecuaciones de esta sección permitirán hacer una estimación del radio de la órbita de un asteroide a estimar a partir de la observación de una sola noche de su movimiento adecuado y distancia angular desde el punto de oposición (asteroide superior) o desde el Sol (asteroide inferior). Los supuestos que se hacen son que la Tierra y el asteroide se encuentran en órbitas circulares coplanares. Si bien este no es el caso de muchos asteroides, es una aproximación razonable para la mayoría de los asteroides al menos en el cinturón principal. Sin embargo, existen algunas combinaciones de\(p\) y\(ε\) para las cuales no se puede obtener una solución, y, para asteroides inferiores, siempre hay dos soluciones posibles.


