13.7: Energía relativista

Objetivos de aprendizaje

Al final de esta sección, podrás:

• Calcular la energía total de un objeto relativista.
• Calcular la energía cinética de un objeto relativista.
• Describir la energía de descanso y explicar cómo se puede convertir a otras formas.
• Explica por qué las partículas masivas no pueden alcanzar C.

Un tokamak es una forma de reactor de fusión experimental, que puede cambiar la masa a energía. Lograr esto requiere una comprensión de la energía relativista. Los reactores nucleares son prueba de la conservación de la energía relativista.

Figura\(\PageIndex{1}\): El Experimento Nacional de Toros Esféricos (NSTX) tiene un reactor de fusión en el que los isótopos de hidrógeno se someten a fusión para producir helio. En este proceso, una masa relativamente pequeña de combustible se convierte en una gran cantidad de energía. (crédito: Princeton Plasma Physics Laboratory)

La conservación de la energía es una de las leyes más importantes de la física. No sólo la energía tiene muchas formas importantes, sino que cada forma se puede convertir a cualquier otra. Sabemos que clásicamente la cantidad total de energía en un sistema permanece constante. Relativisticamente, la energía aún se conserva, siempre que se altere su definición para incluir la posibilidad de que la masa cambie a energía, como en las reacciones que ocurren dentro de un reactor nuclear. La energía relativista se define intencionalmente para que se conserve en todos los marcos inerciales, tal como es el caso del impulso relativista. Como consecuencia, aprendemos que varias cantidades fundamentales están relacionadas de formas desconocidas en la física clásica. Todas estas relaciones son verificadas por experimento y tienen consecuencias fundamentales. La definición alterada de energía contiene algunos de los nuevos conocimientos más fundamentales y espectaculares de la naturaleza encontrados en la historia reciente.

Energía Total y Energía de Descanso

El primer postulado de la relatividad establece que las leyes de la física son las mismas en todos los marcos inerciales. Einstein demostró que la ley de conservación de la energía es válida relativisticamente, si definimos la energía para incluir un factor relativista.

Definición: Total Energy

\(E\)La energía total se define como

\[E = \gamma mc^2,\]

donde\(m\) es la masa,\(c\) es la velocidad de la luz\(\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\), y\(v\) es la velocidad de la masa en relación con un observador.

Hay muchos aspectos de la energía total\(E\) que discutiremos, entre ellos se encuentran cómo se incluyen las energías cinéticas y potenciales\(E\), y cómo\(E\) se relaciona con el impulso relativista. Pero primero, tenga en cuenta que en reposo, la energía total no es cero. Más bien, cuando\(v = 0\), tenemos\(\gamma = 1\), y un objeto tiene energía de descanso.

Definición: Energía de descanso

La energía de descanso es

\[E_0 = mc^2.\]

Esta es la forma correcta de la ecuación más famosa de Einstein, que por primera vez demostró que la energía está relacionada con la masa de un objeto en reposo. Por ejemplo, si la energía se almacena en el objeto, su masa de reposo aumenta. Esto también implica que la masa puede ser destruida para liberar energía. Las implicaciones de estas dos primeras ecuaciones respecto a la energía relativista son tan amplias que no fueron completamente reconocidas durante algunos años después de que Einstein las publicara en 1907, ni tampoco fue la prueba experimental de que son correctas ampliamente reconocidas al principio. Einstein, cabe señalar, sí entendió y describió los significados e implicaciones de su teoría.

Ejemplo\(\PageIndex{1}\): Calculating Rest Energy: Rest Energy is Very Large

Calcular la energía de reposo de una masa de 1.00-g.

Estrategia

Un gramo es una masa pequeña, menos de la mitad de la masa de un centavo. Podemos multiplicar esta masa, en unidades SI, por la velocidad de la luz al cuadrado para encontrar la energía de descanso equivalente.

Solución

1. Identificar los conocidos:\(m = 1.00 \times 10^{-3} \, kg\);\(c = 3.00 \times 10^8 \, m/s\)
2. Identificar lo desconocido:\(E_0\)
3. Elija la ecuación apropiada:\(E_0 = mc^2\)
4. Enchufa los saberes en la ecuación:\[ \begin{align*} E_0 &= mc^2 \\[4pt] &= (1.00 \times 10^{-3} \, kg)(3.00 \times 10^8 \, m/s)^2 \\[4pt] &= 9.00 \times 10^{13} \, kg \cdot m^2/s^2 \end{align*}\]
5. Convertir unidades.

Señalando que\(1 \, kg \cdot m^2/s^2 = 1 \, J\), we see the rest mass energy is \[E_0 = 9.00 \times 19^{13} \, J.\]

Discusión

Esta es una enorme cantidad de energía para una masa de 1.00-g. No notamos esta energía, porque generalmente no está disponible. La energía de reposo es grande porque la velocidad de la luz\(c^2\) es un número muy grande, por lo que\(mc^2\) es enorme para cualquier masa macroscópica. La energía de masa en\(9.00 \times 10^{13} \, J\) reposo para 1.00 g es aproximadamente el doble de la energía liberada por la bomba atómica de Hiroshima y aproximadamente 10,000 veces la energía cinética de un gran portaaviones. Si se puede encontrar una manera de convertir la energía de la masa de reposo en alguna otra forma (y todas las formas de energía se pueden convertir entre sí), entonces se pueden obtener enormes cantidades de energía de la destrucción de la masa.

Hoy en día, son bien conocidas las aplicaciones prácticas de la conversión de la masa en otra forma de energía, como en las armas nucleares y en las centrales nucleares. Pero también existían ejemplos cuando Einstein propuso por primera vez la forma correcta de energía relativista, y sí describió algunos de ellos. La radiación nuclear se había descubierto en la década anterior, y había sido un misterio en cuanto a dónde se originaba su energía. La explicación fue que, en ciertos procesos nucleares, se destruye una pequeña cantidad de masa y la energía es liberada y transportada por la radiación nuclear. Pero la cantidad de masa destruida es tan pequeña que es difícil detectar que falta alguna. Aunque Einstein propuso esto como la fuente de energía en las sales radiactivas que entonces se estaban estudiando, pasaron muchos años antes de que hubiera un amplio reconocimiento de que la masa podría ser y, de hecho, comúnmente se convierte en energía (Figura\(\PageIndex{1}\)).

Figura\(\PageIndex{2}\): El Sol (a) y la Estación Eléctrica de Vapor Susquehanna (b) convierten la masa en energía: el Sol a través de la fusión nuclear, la central eléctrica a través de la fisión nuclear. (créditos: (a) NASA/Goddard Space Flight Center, Scientific Visualization Studio; (b) Gobierno de Estados Unidos)

Debido a la relación de la energía de descanso con la masa, ahora consideramos que la masa es una forma de energía más que algo separado. Ni siquiera había habido un indicio de esto antes de la obra de Einstein. Ahora se sabe que tal conversión es la fuente de la energía del Sol, la energía de la desintegración nuclear, e incluso la fuente de energía que mantiene caliente el interior de la Tierra.

Energía Almacenada y Energía Potencial

¿Qué sucede con la energía almacenada en un objeto en reposo, como la energía que se pone en una batería al cargarla, o la energía almacenada en el resorte comprimido de una pistola de juguete? El aporte de energía se convierte en parte de la energía total del objeto y, así, aumenta su masa de reposo. Toda la energía almacenada y potencial se convierte en masa en un sistema. ¿Por qué es que ordinariamente no nos damos cuenta de esto? De hecho, la conservación de la masa (es decir, la masa total es constante) fue una de las grandes leyes verificadas por la ciencia del siglo XIX. ¿Por qué no se notó que era incorrecto? El siguiente ejemplo ayuda a responder estas preguntas.

Ejemplo\(\PageIndex{2}\): Calculating Rest Mass: A Small Mass Increase due to Energy Input

La batería de un automóvil está clasificada para poder mover 600 amperios-hora\(( \cdot h)\) de carga a 12.0 V.

1. Calcular el aumento en la masa de reposo de una batería de este tipo cuando se toma de estar completamente agotada a estar completamente cargada.
2. ¿Qué porcentaje de incremento es este, dado que la masa de la batería es de 20.0 kg?

Estrategia

En la parte (a), primero debemos encontrar la energía almacenada en la batería, lo que equivale a lo que la batería puede suministrar en forma de energía potencial eléctrica. Ya que\(PE_{elec} = qV\), tenemos que calcular la carga\(q\) en\(600 \, A \cdot h\), que es producto de la corriente\(I\) y el tiempo\(t\). Luego multiplicamos el resultado por 12.0 V. Entonces podemos calcular el aumento de masa de la batería usando\(\Delta E = PE_{elec} = (\Delta m)c^2\).

La parte (b) es una relación simple convertida a un porcentaje.

Solución para (a)

1. Identificar los conocidos:\(I \cdot t = 600 \, A \cdot h\);\(V = 12.0 \, V\);\(c = 3.00 \times 10^8 \, m/s\)
2. Identificar lo desconocido:\(\delta m\)
3. Elija la ecuación apropiada:\(PE_{elec} = (\Delta m)c^2\)
4. Reorganizar la ecuación para resolver por lo desconocido:\(\Delta m = \frac{PE_{elec}}{c^2}\)
5. Enchufa los conocimientos en la ecuación:\[ \Delta m = \dfrac{PE_{elec}}{c^2} = \dfrac{qV}{c^2} = \dfrac{(It)V}{c^2} = \dfrac{(600 \, A \cdot h)(12.0 \, V)}{(3.00 \times 10^8)^2}.\] Escribe amperios A como culombios por segundo (C/s), y convierte horas en segundos. \[\Delta m = \dfrac{(600 \, C/s \cdot h(\frac{3600 \, s}{1 \, h})(12.0 \, J/C)}{3.00 \times 10^8 \, m/s)^2}\]\[ = \dfrac{(2.16 \times 10^6 \, C)(12.0 \, J/C)}{(3.00 \times 10^8 \, m/s)^2}\]Usando la conversión\(1 \, kg \cdot m^2/c^2 = 1 \, J\), podemos escribir la masa como\(\delta m = 2.88 \times 10^{-10} \, kg\).

Solución para (b)

1. Identificar los conocidos:\(\Delta m = 2.88 \times 10^{-10} \, kg\);\(m = 20.0 \, kg\)
2. Identificar lo desconocido:% de cambio
3. Elija la ecuación apropiada:\(\% \, increase = \frac{\Delta m}{m} \times 100\%\)
4. Enchufa los saberes en la ecuación:\[\% \, increase = \dfrac{\delta m}{m} \times 100\% = \dfrac{2.88 \times 10^{-10} \, kg}{20.0 \, kg} \times 100\% = 1.44 \times 10^{-9}\%\]

Discusión

Tanto el incremento real de masa como el incremento porcentual son muy pequeños, ya que la energía se divide por\(c^2\), un número muy grande. Tendríamos que ser capaces de medir la masa de la batería con una precisión de mil millonésima parte de un por ciento, o 1 parte adentro\(10^{11}\), para notar este incremento. No es de extrañar que la variación de masa no se observe fácilmente. De hecho, este cambio en la masa es tan pequeño que podemos cuestionarnos cómo podrías verificar que es real. La respuesta se encuentra en procesos nucleares en los que el porcentaje de masa destruida es lo suficientemente grande como para ser medido. La masa del combustible de un reactor nuclear, por ejemplo, es mensurablemente menor cuando se ha utilizado su energía. En ese caso, se ha liberado la energía almacenada (convertida principalmente en calor y electricidad) y la masa restante ha disminuido. Este es también el caso cuando se utiliza la energía almacenada en una batería, salvo que la energía almacenada es mucho mayor en los procesos nucleares, haciendo que el cambio de masa sea mensurable tanto en la práctica como en la teoría.

Energía cinética y el límite máximo de velocidad

La energía cinética es la energía del movimiento. Clásicamente, la energía cinética tiene la expresión familiar\(\frac{1}{2} mv^2\). La expresión relativista para la energía cinética se obtiene del teorema trabajo-energía. Este teorema afirma que el trabajo neto en un sistema entra en energía cinética. Si nuestro sistema parte del descanso, entonces el teorema trabajo-energía es

\[W_{net} = KE.\]

Relativisticamente, en reposo tenemos energía de descanso\(E_0 = mc^2\). El trabajo aumenta esto a la energía total\(E = \gamma mc^2\). Por lo tanto,

\[W_{net} = E - E_0 = \gamma mc^2 - mc^2 = (\gamma - 1)mc^2.\]

Relativisticamente, tenemos\(W_{net} = KE_{rel}.\)

Definición: Energía cinética relativista

La energía cinética relativista es

\[KE_{rel} = (\gamma - 1)mc^2.\]

Cuando estamos inmóviles, tenemos\(v = 0\) y

\[\gamma = \dfrac{1}{\sqrt{1 - \frac{v^2}{c^2}}} = 1,\]

para que\(KE_{rel} = 0\) en reposo, como se esperaba. Pero la expresión de energía cinética relativista (como energía total y energía de reposo) no se parece mucho\(\frac{1}{2}mv^2\) a la clásica Para mostrar que la expresión clásica de energía cinética se obtiene a bajas velocidades, observamos que la expansión\(\gamma\) binomial para a bajas velocidades da

\[\gamma = 1 + \dfrac{1}{2} \dfrac{v^2}{c^2}.\]

Introducir esto en la expresión de energía cinética relativista da

\[KE_{rel} = \left[\dfrac{1}{2} \dfrac{v^2}{c^2} \right] mc^2 = \dfrac{1}{2}mv^2 = KE_{class}.\]

Entonces, de hecho, la energía cinética relativista sí se convierte en lo mismo que la energía cinética clásica cuando\(v < < c\).

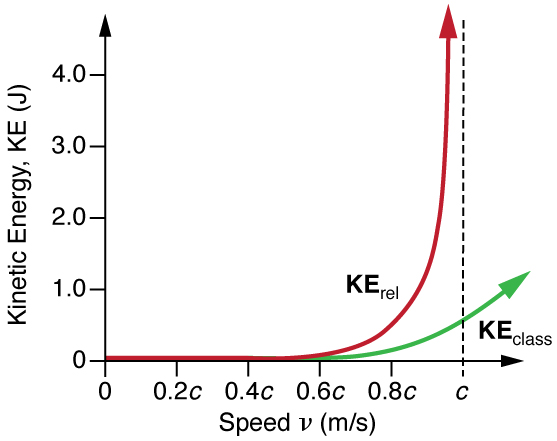
Es aún más interesante investigar qué sucede con la energía cinética cuando la velocidad de un objeto se acerca a la velocidad de la luz. Sabemos que\(\gamma\) se vuelve infinito a medida que se\(v\) acerca\(c\), de modo que\(KE_{rel}\) también se vuelve infinito a medida que la velocidad se acerca a la velocidad de la luz (Figura\(\PageIndex{1}\)). Se requiere una cantidad infinita de trabajo (y, por lo tanto, una cantidad infinita de entrada de energía) para acelerar una masa a la velocidad de la luz.

Definición: Velocidad de la luz

Ningún objeto con masa puede alcanzar la velocidad de la luz.

Entonces, la velocidad de la luz es el límite máximo de velocidad para cualquier partícula que tenga masa. Todo esto es consistente con el hecho de que las velocidades menores que\(c\) siempre se suman a menos de\(c\). Tanto la forma relativista para la energía cinética como el límite de velocidad final se\(c\) han confirmado en detalle en numerosos experimentos. No importa cuánta energía se ponga en acelerar una masa, su velocidad solo puede acercarse, no alcanzar, la velocidad de la luz.

Figura\(\PageIndex{3}\): Esta gráfica\(KE_{rel}\) versus velocidad muestra cómo la energía cinética se acerca al infinito a medida que la velocidad se acerca a la velocidad de la luz. Por lo tanto, no es posible que un objeto que tenga masa alcance la velocidad de la luz. También se muestra\(KE_{class}\), la energía cinética clásica, que es similar a la energía cinética relativista a bajas velocidades. Tenga en cuenta que se requiere mucha más energía para alcanzar velocidades altas de lo que se predijo clásicamente.

Ejemplo\(\PageIndex{3}\): Comparing Kinetic Energy: Relativistic Energy Versus Classical Kinetic Energy

Un electrón tiene una velocidad\(v = 0.990 c\).

1. Calcular la energía cinética en MeV del electrón.
2. Compare esto con el valor clásico de la energía cinética a esta velocidad. (La masa de un electrón es\(9.11 \times 10^{-31} \, kg\).)

Estrategia

La expresión de energía cinética relativista siempre es correcta, pero para (a) debe ser utilizada ya que la velocidad es altamente relativista (cercana a\(c\)). Primero, calcularemos el factor relativista\(\gamma\), y luego lo usaremos para determinar la energía cinética relativista. Para (b), calcularemos la energía cinética clásica (que estaría cerca del valor relativista si\(v\) fueran menores a un pequeño porcentaje de\(c\)) y veremos que no es lo mismo.

Solución para (a)

1. Identificar los conocidos:\(v = 0.990 c\);\(m = 9.11 \times 10^{-31} \, kg\)
2. Identificar lo desconocido:\(KE_{rel}\)
3. Elija la ecuación apropiada\(KE_{rel} = (\gamma - 1) mc^2\)
4. Enchufa los conocimientos en la ecuación:

Primero calcule\(\gamma\). Llevaremos dígitos adicionales porque se trata de un cálculo intermedio.

\[\gamma = \dfrac{1}{\sqrt{1 - \frac{v^2}{c^2}}} = \dfrac{1}{\sqrt{1 - \frac{(0.990 c)^2}{c^2}}} = \dfrac{1}{\sqrt{1 - (0.990)^2}} = 7.0888\]

A continuación, utilizamos este valor para calcular la energía cinética.

\[KE_{rel} = (\gamma - 1)mc^2 = (7.0888 -1)(9.11 \times 10^{-31} \, kg)(3.00 \times 10^8 \, m/s)^2 = 4.99 \times 10^{-13} \, J\]

5. Convertir unidades:

\[KE_{rel} = (4.99 \times 10^{-13} \, J)\left( \dfrac{1 \, MeV}{1.60 \times 10^{-13} \, J} \right) = 3.12 \, MeV\]

Solución para (b)

1. Enumere los saberes:\(v = 0.990 c\);\(m = 9.11 \times 10^{-31} \, kg\)
2. Enumere lo desconocido:\(KE_{class}\)
3. Elija la ecuación apropiada:\(KE_{class} = \frac{1}{2} mv^2\)
4. Enchufa los conocimientos en la ecuación:\[KE_{class} = \dfrac{1}{2} mv^2\]\[ = \dfrac{1}{2}(9.11 \times 10^{-31} \, kg)(0.990)^2(3.00 \times 10^8 \, m/s)^2\]\[= 4.02 \times 10^{-14} \, J\]
5. Convertir unidades:\[KE_{class} = 4.02 \times 10^{-14} \, \left(\dfrac{1 \, MeV}{1.60 \times 10^{-13} \, J}\right) = 0.251 \, MeV\]

Discusión

Como podría esperarse, dado que la velocidad es 99.0% de la velocidad de la luz, la energía cinética clásica está significativamente alejada del valor relativista correcto. Obsérvese también que el valor clásico es mucho menor que el valor relativista. De hecho,\(KE_{rel}/KE_{class} = 12.4\) aquí. Esto es una indicación de lo difícil que es conseguir que una masa se mueva cerca de la velocidad de la luz. Se requiere mucha más energía de la que se predijo clásicamente. Algunas personas interpretan esta energía extra como que va a aumentar la masa del sistema, pero, como se discute en Momentum relativista, esto no se puede verificar sin ambigüedades. Lo cierto es que se necesitan cantidades cada vez mayores de energía para acercar un poco la velocidad de una masa a la de la luz. Una energía de 3 MeV es una cantidad muy pequeña para un electrón, y se puede lograr con aceleradores de partículas actuales. SLAC, por ejemplo, puede acelerar los electrones a más\(50 \times 10^9 \, eV = 50,000 MeV\).

¿Tiene algún sentido acercarse\(v\) un poco más a c que 99.0% o 99.9%? La respuesta es sí. Aprendemos mucho haciendo esto. La energía que entra en una masa de alta velocidad se puede convertir a cualquier otra forma, incluso en masas completamente nuevas. (Ver Figura.) La mayor parte de lo que sabemos sobre la subestructura de la materia y la colección de partículas exóticas de corta duración en la naturaleza se ha aprendido de esta manera. Las partículas se aceleran a energías extremadamente relativistas y se hacen colisionar con otras partículas, produciendo especies de partículas totalmente nuevas. Los patrones en las características de estas partículas previamente desconocidas apuntan a una subestructura básica para toda la materia. Estas partículas y algunas de sus características serán cubiertas en Física de Partículas.

Figura\(\PageIndex{4}\): El Laboratorio Nacional Acelerador Fermi, cerca de Batavia, Illinois, fue un colisionador de partículas subatómicas que aceleró protones y antiprotones para alcanzar energías de hasta 1 Tev (un billón de electronvoltios). Los estanques circulares cerca de los anillos fueron construidos para disipar el calor residual. Este acelerador se apagó en septiembre de 2011. (crédito: Fermilab, Reidar Hahn)

Energía relativista e impulso

Sabemos clásicamente que la energía cinética y el impulso están relacionados entre sí, ya que\[KE_{class} = \dfrac{p^2}{2m} = \dfrac{(mv)^2}{2m} = \dfrac{1}{2} mv^2.\]

Relativisticamente, podemos obtener una relación entre energía e impulso manipulando algebraicamente sus definiciones. Esto produce

\[E^2 = (pc)^2 + (mc^2)^2,\]

donde\(E\) está la energía total relativista y\(p\) es el impulso relativista. Esta relación entre la energía relativista y el impulso relativista es más complicada que la clásica, pero podemos obtener algunas nuevas ideas interesantes al examinarla. Primero, la energía total está relacionada con el impulso y la masa de descanso. En reposo, el impulso es cero, y la ecuación da la energía total para que sea la energía de descanso\(mc^2\) (por lo que esta ecuación es consistente con la discusión de la energía de descanso anterior). Sin embargo, a medida que se acelera la masa, su impulso\(p\) aumenta, incrementando así la energía total. A velocidades suficientemente altas, el término de energía de descanso\((mc^2)^2\) se vuelve insignificante en comparación con el término impulso\((pc)^2\); así,\(E = pc\) a velocidades extremadamente relativistas.

Si consideramos que el impulso\(p\) es distinto de la masa, podemos determinar las implicaciones de la ecuación\(E^2 = (pc)^2 + (mc^2)^2\), para una partícula que no tiene masa. Si tomamos\(m\) para ser cero en esta ecuación, entonces\(E = pc\), o\(p = E/c\). Las partículas sin masa tienen este impulso. Hay varias partículas sin masa que se encuentran en la naturaleza, incluyendo fotones (estos son cuantos de radiación electromagnética). Otra implicación es que una partícula sin masa debe viajar a velocidad\(c\) y sólo a velocidad\(c\). Si bien está más allá del alcance de este texto examinar la relación en la ecuación\(E^2 = (pc)^2 + (mc^2)^2\), en detalle, podemos ver que la relación tiene implicaciones importantes en la relatividad especial.

Estrategias de resolución de problemas para la relatividad

1. Examinar la situación para determinar que es necesario utilizar la relatividad. Los efectos relativistas están relacionados\(\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\) con el factor relativista cuantitativo. Si\(\gamma\) está muy cerca de 1, entonces los efectos relativistas son pequeños y difieren muy poco de los cálculos clásicos generalmente más fáciles.
2. Identificar exactamente lo que hay que determinar en el problema (identificar las incógnitas).
3. Hacer una lista de lo que se da o se puede inferir del problema como se indica (identificar los conocimientos). Busque en particular información sobre la velocidad relativa\(v\).
4. Asegurese de comprender los aspectos conceptuales del problema antes de hacer cualquier cálculo. Decidir, por ejemplo, qué observador ve el tiempo dilatado o la longitud contraída antes de enchufarse a las ecuaciones. Si has pensado en quién ve qué, quién se mueve con el evento que se observa, quién ve el tiempo adecuado, y así sucesivamente, te resultará mucho más fácil determinar si tu cálculo es razonable.
5. Determinar el tipo primario de cálculo a realizar para encontrar las incógnitas identificadas anteriormente. Encontrará útil el resumen de la sección para determinar si está involucrada una contracción de longitud, energía cinética relativista o algún otro concepto.
6. No redondear durante el cálculo. Como se señala en el texto, a menudo debes realizar tus cálculos a muchos dígitos para ver el efecto deseado. Puede redondear al final del problema, pero no utilice un número redondeado en un cálculo posterior.
7. Consulta la respuesta para ver si es razonable: ¿Tiene sentido? Esto puede ser más difícil para la relatividad, ya que no la encontramos directamente. Pero se pueden buscar velocidades mayores\(c\) o efectos relativistas que están en la dirección equivocada (como una contracción de tiempo donde se esperaba una dilatación).

Ejercicio\(\PageIndex{1}\)

Un fotón decae en un par electrón-positrón. ¿Cuál es la energía cinética del electrón si su velocidad es\(0.992 c\)?

Contestar

\[\begin{align*} KE_{rel} &= (\gamma -1)mc^2 \\[5pt] &= \left(\dfrac{1}{\sqrt{1 - \frac{v^2}{c^2}}} - 1\right) mc^2 \\[5pt] &= \left( \dfrac{1}{\sqrt{1 - \frac{(0.992 c)^2}{c^2}}} - 1\right) (9.11 \times 10^{-31} \, kg)(3.00 \times 10^8 \, m/s)^2 \\[5pt] &= 5.67 \times 10^{-13} \, J \end{align*}\]

Resumen

• La energía relativista se conserva siempre y cuando la definamos para incluir la posibilidad de que la masa cambie a energía.
• La Energía Total se define como:\(E = \gamma mc^2\), donde\(\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\)
• La energía de descanso es\(E_0 = mc^2\), es decir, que la masa es una forma de energía. Si la energía se almacena en un objeto, su masa aumenta. La masa puede ser destruida para liberar energía.
• Normalmente no notamos el aumento o disminución de la masa de un objeto porque el cambio en la masa es tan pequeño para un gran aumento de energía.
• El teorema relativista de trabajo-energía es\(W_{net} = E - E_0 = \gamma mc^2 = (\gamma - 1) mc^2\).
• Relativista,\(W_{net} = KE_{rel}\), donde\(KE_{rel}\) está la energía cinética relativista.
• La energía cinética relativista es\(KE_{rel} = (\gamma - 1) mc^2\), dónde\(\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\). A bajas velocidades, la energía cinética relativista se reduce a la energía cinética clásica.
• Ningún objeto con masa puede alcanzar la velocidad de la luz porque se requiere una cantidad infinita de trabajo y una cantidad infinita de entrada de energía para acelerar una masa a la velocidad de la luz.
• La ecuación\(E^2 = (pc)^2 + (mc^2)^2\) relaciona la energía total relativista\(E\) y el impulso relativista\(p\). A velocidades extremadamente altas, la energía de reposo\(mc^2\) se vuelve insignificante, y\(E = pc\).

Glosario

energía total

definido como\(E = \gamma mc^2\), donde\(\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\)

energía de descanso

la energía almacenada en un objeto en reposo:\(E_0 = mc^2\)

energía cinética relativista

la energía cinética de un objeto que se mueve a velocidades relativistas:\(KE_{rel} = (\gamma -1) mc^2\), donde\(\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\)