4.4: El Plano Complejo

Una manera conveniente de conceptualizar un número complejo es pensarlo como un punto en un plano bidimensional, llamado plano complejo, como se muestra en la siguiente figura. Las partes real e imaginaria son las coordenadas cartesianas horizontales y verticales en el plano. Los ejes de coordenadas horizontal (\(x\)\(y\)) y vertical () se denominan “eje real” y “eje imaginario”, respectivamente.

Figura\(\PageIndex{1}\)

Representación polar

Si pensamos en un número complejo como un punto en el plano complejo, su posición también se puede representar usando coordenadas polares en lugar de coordenadas cartesianas. Para un número complejo\(z = x + i y\), podemos introducir coordenadas polares\(r\) y\(\theta\) (ambos números reales), tal que a la\[r = \sqrt{x^2 + y^2}, \;\;\; \theta = \tan^{-1}(y/x).\] inversa,\[x = r\cos\theta, \;\;\; y = r\sin\theta.\] Estas son las fórmulas habituales para realizar un cambio de coordenada entre coordenadas cartesianas bidimensionales y coordenadas polares, como se muestra a continuación. La coordenada radial es la magnitud del número complejo:\(r = |z|\). A la coordenada azimutal\(\theta\) se le llama el argumento del número complejo, que también se denota por\(\mathrm{arg}(z)\).

Figura\(\PageIndex{2}\)

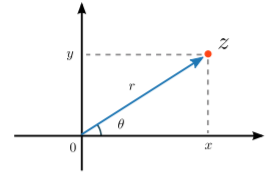
Tenga en cuenta, por cierto, que el cero complejo,\(z = 0\), tiene magnitud cero y argumento indefinido.

Usando la fórmula de Euler (4.3.1), podemos escribir\[\begin{align} z &= r\cos(\theta) + i r\sin(\theta)\\ &= r \left[\cos(\theta) + i \sin(\theta)\right] \\ &= r \, e^{i\theta}.\end{align}\] Por lo tanto, siempre que podamos manipular un número complejo en una forma\(A e^{iB}\), donde\(A\) y\(B\) son números reales, entonces\(A\) es la magnitud y\(B\) es la argumento. Esto se utiliza en el siguiente ejemplo:

Ejemplo\(\PageIndex{1}\)

Pues\(z \in \mathbb{C}\), se puede demostrar que la magnitud y el argumento de\(\exp(z)\) son:\[\left|\exp(z)\right| = e^{\mathrm{Re}(z)}, \quad \mathrm{arg}\left[\exp(z)\right] = \mathrm{Im}(z).\] Prueba: Vamos\(z = x + i y\), donde\(x, y \in \mathbb{R}\); entonces\[e^{z} = e^{x + i y} = e^x \, e^{iy}.\] Por inspección, la magnitud de este número complejo es\(e^x\), y su argumento es \(y\).

Interpretación geométrica de operaciones complejas

Usando el plano complejo, podemos dar interpretaciones geométricas útiles a las operaciones básicas sobre números complejos:

• La adición de dos números complejos se puede interpretar como la adición de dos vectores de coordenadas. Si\(z_1 = x_1 + i y_1\) y\(z_2 = x_2 + i y_2\), entonces\[z_1 + z_2 = \left(x_1 + x_2\right) + i\left(y_1 + y_2\right).\] Por lo tanto, el punto correspondiente a\(z_1 + z_2\) se obtiene sumando los dos vectores de coordenadas correspondientes a\(z_1\) y\(z_2\). A partir de esto, podemos probar geométricamente una relación de desigualdad útil entre números complejos, llamada la “desigualdad triangular”:\[|z_1 + z_2| \le |z_1| + |z_2|.\]

• La multiplicación compleja se puede interpretar como una escala junto con una rotación. Si\(z_1 = r_1e^{i\theta_1}\) y\(z_2 = r_2e^{i\theta_2}\), entonces\[z_1 z_2 = \left(r_1 r_2\right) \,\exp[i(\theta_1 + \theta_2)].\] Por lo tanto, el punto correspondiente a\(z_1 \, z_2\) se obtiene escalando el vector de\(z_1\) coordenadas por un factor de\(|z_2|\), y girándolo por un ángulo de\(\theta_2\) alrededor del origen. En particular, la multiplicación por\(e^{i\theta}\) equivale a una rotación por ángulo\(\theta\).

• La operación de conjugación (Sección 4.2) equivale a la reflexión sobre el eje real. Se mueve un punto desde la mitad superior del plano complejo a la mitad inferior, o viceversa.

Los números complejos no tienen orden

Una consecuencia del hecho de que los números complejos residen en un plano bidimensional es que las relaciones de desigualdad son indefinidas para los números complejos. Esta es una diferencia importante entre números complejos y reales.

Los números reales se pueden ordenar, es decir, que para dos números reales cualesquiera\(a\) y\(b\), uno y solo uno de los siguientes es cierto:\[a < b \;\; \mathrm{OR} \;\; a = b \;\; \mathrm{OR}\;\; a > b.\] En términos geométricos, estas relaciones de orden existen porque los números reales residen a lo largo de una línea unidimensional.

Pero como los números complejos se encuentran en un plano bidimensional, no tiene sentido escribir algo así como\(z_1 < z_2\), dónde\(z_1\) y\(z_2\) son números complejos. (Es, sin embargo, válido escribir\(|z_1| < |z_2|\), ya que las magnitudes son reales.)