4.6: Trayectorias en el Plano Complejo
- Page ID
- 125945
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Si tenemos una función\(z(t)\) que toma una entrada real\(t\) y da salida a un número complejo\(z\), a menudo es útil trazar una curva en el plano complejo llamada la “trayectoria paramétrica” de\(z\). Cada punto de esta curva indica el valor de\(z\) para un valor particular de\(t\). A continuación daremos algunos ejemplos.
Primero, considere\[z(t) = e^{i\omega t}, \quad \omega \in \mathbb{R}.\] La trayectoria es un círculo en el plano complejo, centrado en el origen y con radio 1:

Para ver por qué, observar que la función tiene la forma\(z(t) = r(t)\,e^{i\theta(t)}\), que tiene magnitud\(r(t) = 1\), y argumento que\(\theta(t) = \omega t\) varía proporcionalmente con\(t\). Si\(\omega\) es positivo, el argumento aumenta con\(t\), por lo que la trayectoria es en sentido antihorario. Si\(\omega\) es negativo, la trayectoria es en sentido horario.
A continuación, considere\[z(t) = e^{(\gamma + i \omega) t},\] dónde\(\gamma,\omega \in \mathbb{R}.\) For\(\gamma = 0\), esto se reduce al ejemplo anterior. Porque\(\gamma \ne 0\), la trayectoria es una espiral:
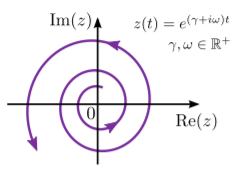
Para ver esto, nuevamente observamos que esta función se puede escribir en la forma\[z(t) = r(t) \;e^{i\theta(t)},\] donde\(r(t) = e^{\gamma t}\) y\(\theta = \omega t.\) El argumento varía proporcionalmente con\(t\), por lo que la trayectoria gira alrededor del origen. La magnitud aumenta con\(t\) si\(\gamma\) es positivo, y disminuye con\(t\) si\(\gamma\) es negativo. Así, por ejemplo, si\(\gamma\) y ambos\(\omega\) son positivos, entonces la trayectoria es una espiral en sentido antihorario que se mueve hacia afuera desde el origen. Intenta verificar cómo se comporta la trayectoria cuando los signos de\(\gamma\) y/o\(\omega\) están volteando.
Por último, considere\[z(t) = \frac{1}{\alpha t + \beta}, \quad \alpha, \beta \in \mathbb{C}.\] Esta trayectoria es un círculo que pasa por el origen, como se muestra a continuación:
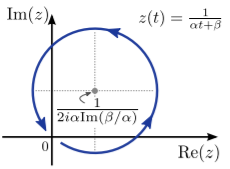
Mostrar esto requiere un poco de ingenio, y se deja como ejercicio. Este es un ejemplo de algo llamado una transformación de Möbius.


