10.6: Transformadas comunes de Fourier

Para acumular más intuición sobre las transformaciones de Fourier, examinemos las transformaciones de Fourier de algunas funciones interesantes. Simplemente vamos a exponer los resultados; los cálculos se dejan como ejercicios.

Olas amortiguadas

Vimos en la Sección 10.2 que una función de decaimiento exponencial con constante de decaimiento\(\eta \in \mathbb{R}^+\) tiene la siguiente transformada de Fourier:\[f(x) = \left\{\begin{array}{cl}e^{-\eta x}, & x \ge 0 \\ 0, & x < 0,\end{array}\right. \;\; \overset{\mathrm{FT}}{\longrightarrow} \;\; F(k) = \frac{-i}{k-i\eta}.\] Observe que\(F(k)\) viene dada por una fórmula algebraica simple. Si “extendemos” el dominio de\(k\) a valores complejos,\(F(k)\) corresponde a una función analítica con un polo simple en la mitad superior del plano complejo, at\(k = i\eta\).

A continuación, considere una onda en descomposición con número de onda\(q \in \mathbb{R}\) y constante de decaimiento\(\eta \in \mathbb{R}^+\). La transformada de Fourier es una función con un polo simple en\(q + i \eta\):\[f(x) = \left\{\begin{array}{cl}e^{i (q + i\eta) x}, & x \ge 0 \\ 0, & x < 0.\end{array}\right. \;\; \overset{\mathrm{FT}}{\longrightarrow} \;\; F(k) = \frac{-i}{k-(q + i\eta)}.\]

Por otro lado, considera una ola que crece exponencialmente con\(x\) for\(x < 0\), y es cero para\(x > 0\). La transformada de Fourier es una función con un polo simple en el semiplano inferior:\[f(x) = \left\{\begin{array}{cl}0, & x \ge 0 \\ e^{i (q - i\eta) x}, & x < 0.\end{array}\right. \;\; \overset{\mathrm{FT}}{\longrightarrow} \;\; F(k) = \frac{i}{k-(q - i\eta)}.\] A partir de estos ejemplos, vemos que las oscilaciones y amplificación/decaimiento en\(f(x)\) están relacionadas con la existencia de polos en la expresión algebraica para\(F(k)\). La parte real de la posición de polo da el número de onda de la oscilación, y la distancia desde el polo al eje real da la constante de amplificación o decaimiento. Una señal en descomposición produce un polo en el medio plano superior, mientras que una señal que aumenta exponencialmente\(x\) produce un polo en el medio plano inferior. En ambos casos, si trazamos el espectro de Fourier\(|F(k)|^2\) versus real\(k\), el resultado es un pico lorentziano centrado en\(k = q\), con ancho\(2\eta\).

Paquetes de ondas gaussianas

Considere una función con una envolvente de decaimiento dada por una función gaussiana:\[f(x) = e^{iq x} \, e^{-\gamma x^2}, \;\;\;\mathrm{where}\; q \in \mathbb{C},\; \gamma \in \mathbb{R}.\] Esto se llama paquete de ondas gaussianas. El ancho de la envolvente generalmente se caracteriza por la desviación estándar de la función gaussiana, que es donde la curva alcanza\(e^{-1/2}\) por su valor máximo. En este caso, la desviación estándar es\(\Delta x = 1/\sqrt{2\gamma}\).

Mostraremos que\(f(x)\) tiene la siguiente transformada de Fourier:\[F(k) = \sqrt{\frac{\pi}{\gamma}} \, e^{-\frac{(k-q)^2}{4\gamma}}.\]

Para derivar este resultado, realizamos la integral de Fourier de la siguiente manera:\[\begin{align} F(k) &= \int_{-\infty}^\infty dx \, e^{-ikx}\, f(x) \\ &= \int_{-\infty}^\infty dx \, \exp\left\{-i(k-q)x -\gamma x^2\right\}.\end{align}\] En el integrando, la expresión dentro de lo exponencial es cuadrática en\(x\). Completamos el cuadrado:\[\begin{align} F(k) &= \int_{-\infty}^\infty dx \, \exp\left\{-\gamma\left(x + \frac{i(k-q)}{2\gamma}\right)^2 + \gamma\left(\frac{i(k-q)}{2\gamma}\right)^2\right\} \\ &= \exp\left\{ - \frac{(k-q)^2}{4\gamma}\right\}\; \int_{-\infty}^\infty dx \, \exp\left\{-\gamma\left(x + \frac{i(k-q)}{2\gamma}\right)^2\right\}.\end{align}\] La integral restante es la integral gaussiana con un cambio imaginario constante en\(x\). Al desplazar la variable de integración, se puede demostrar que ésta es igual a la integral gaussiana estándar,\(\sqrt{\pi/\gamma}\); los detalles se dejan como ejercicio. De esta manera llegamos al resultado señalado anteriormente.

El espectro de Fourier,\(|F(k)|^2\), es una función gaussiana con desviación estándar\[\Delta k = \frac{1}{\sqrt{2(1/2\gamma)}} = \sqrt{\gamma}.\]

Figura\(\PageIndex{1}\)

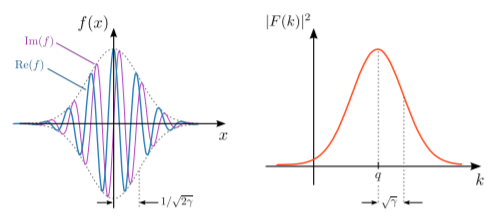
Una vez más, el espectro de Fourier alcanza su punto máximo a un valor\(k\) correspondiente al número de onda de la onda sinusoidal subyacente en\(f(x)\), y una disminución más fuerte (más débil)\(f(x)\) conduce a un espectro de Fourier más amplio (más estrecho). Estas características se pueden observar en la parcela anterior.