14.3: La Segunda Ley de la Termodinámica
- Page ID
- 128077
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)objetivos de aprendizaje
- Contraste el concepto de irreversibilidad entre la Primera y Segunda Ley de la Termodinámica
Irreversibilidad
La segunda ley de la termodinámica se ocupa de la dirección que toman los procesos espontáneos. Muchos procesos ocurren espontáneamente en una sola dirección, es decir, son irreversibles, bajo un conjunto dado de condiciones. Si bien la irreversibilidad se ve en la vida cotidiana —los vidrios rotos no retoman su estado original, por ejemplo—, la irreversibilidad completa es una afirmación estadística que no se puede ver durante la vida del universo. Más precisamente, un proceso irreversible es aquel que depende del camino. Si el proceso puede ir en una sola dirección, entonces el camino inverso difiere fundamentalmente y el proceso no puede ser reversible.
Por ejemplo, el calor implica la transferencia de energía de mayor a menor temperatura. Un objeto frío en contacto con uno caliente nunca se enfría más, transfiriendo calor al objeto caliente y haciéndolo más caliente. Además, la energía mecánica, como la energía cinética, se puede convertir completamente en energía térmica por fricción, pero lo contrario es imposible. Un objeto estacionario caliente nunca se enfría espontáneamente y comienza a moverse. Otro ejemplo más es la expansión de una bocanada de gas introducida en una esquina de una cámara de vacío. El gas se expande para llenar la cámara, pero nunca se reagrupa en la esquina. El movimiento aleatorio de las moléculas de gas podría llevarlas a todas de vuelta a la esquina, pero esto nunca se observa que suceda.

Procesado unidireccional en la naturaleza: Ejemplos de procesos unidireccionales en la naturaleza. (a) La transferencia de calor ocurre espontáneamente de caliente a frío y no de frío a caliente. (b) Los frenos de este automóvil convierten su energía cinética en transferencia de calor al medio ambiente. El proceso inverso es imposible. (c) El estallido de gas que entra en esta cámara de vacío se expande rápidamente para llenar uniformemente cada parte de la cámara. Los movimientos aleatorios de las moléculas de gas nunca las devolverán a la esquina.
Segunda Ley de Termodinámica
El hecho de que ciertos procesos nunca ocurran sugiere que existe una ley que prohíbe que ocurran. La primera ley de la termodinámica permitiría que ocurrieran, ninguno de esos procesos viola la conservación de la energía. A la ley que prohíbe estos procesos se le llama la segunda ley de la termodinámica. Veremos que la segunda ley se puede afirmar de muchas maneras que pueden parecer diferentes, pero estas muchas formas son, de hecho, equivalentes. Como todas las leyes naturales, la segunda ley de la termodinámica da ideas sobre la naturaleza, y sus diversas afirmaciones implican que es ampliamente aplicable, afectando fundamentalmente a muchos procesos aparentemente dispares. La ya familiar dirección de transferencia de calor de caliente a frío es la base de nuestra primera versión de la segunda ley de la termodinámica.
Termodinámica y Motores Térmicos: Una breve introducción a los motores térmicos y conceptos termodinámicos como el Motor Carnot para estudiantes.
La Segunda Ley de la Termodinámica (primera expresión): La transferencia de calor ocurre espontáneamente de cuerpos de temperatura superior a baja pero nunca espontáneamente en sentido inverso.
La ley establece que es imposible que cualquier proceso tenga como único resultado la transferencia de calor de un refrigerador a un objeto más caliente. Vamos a expresar la ley en otros términos más adelante, lo más importante en términos de entropía.
Motores de Calor
En termodinámica, un motor térmico es un sistema que realiza la conversión de calor o energía térmica en trabajo mecánico.
objetivos de aprendizaje
- Justifica por qué la eficiencia es uno de los parámetros más importantes para cualquier motor térmico
En termodinámica, un motor térmico es un sistema que realiza la conversión de calor o energía térmica en trabajo mecánico. Los motores de gasolina y diesel, los motores a reacción y las turbinas de vapor son todos motores de calor que funcionan al usar parte de la transferencia de calor de alguna fuente. La transferencia de calor desde el objeto caliente (o reservorio caliente) se denota como Q h, mientras que la transferencia de calor al objeto frío (o reservorio frío) es Q c, y el trabajo realizado por el motor es W. Las temperaturas de los depósitos caliente y frío son T h y T c, respectivamente.
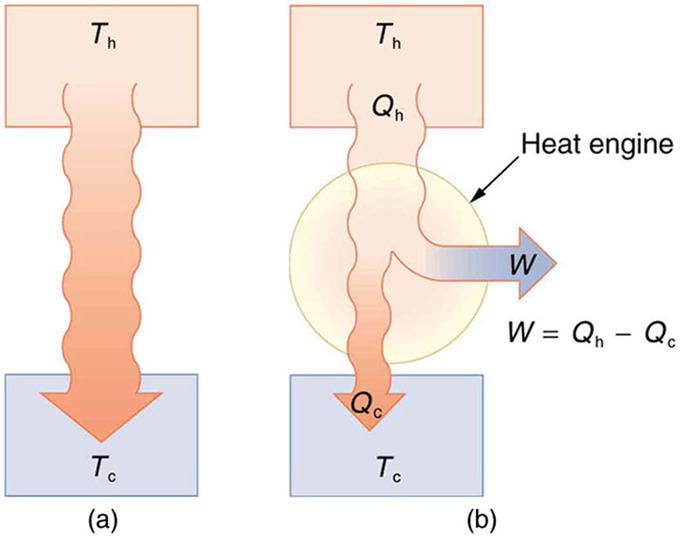
Transferencia de Calor: (a) La transferencia de calor ocurre espontáneamente de un objeto caliente a uno frío, consistente con la segunda ley de la termodinámica. (b) Un motor térmico, representado aquí por un círculo, utiliza parte de la transferencia de calor para realizar el trabajo. A los objetos fríos y calientes se les llama depósitos fríos y calientes. Qh es la transferencia de calor fuera del depósito caliente, W es la salida de trabajo y Qc es la transferencia de calor al depósito frío.
Termodinámica y Motores Térmicos: Una breve introducción a los motores térmicos y conceptos termodinámicos como el Motor Carnot para estudiantes.
Debido a que el reservorio caliente se calienta externamente, lo que consume mucha energía, es importante que el trabajo se realice de la manera más eficiente posible. De hecho, nos gustaría que W sea igual a Q h, y que no haya transferencia de calor al ambiente (Q c =0). Desafortunadamente, esto es imposible. La segunda ley de la termodinámica (segunda expresión) también establece, con respecto al uso de la transferencia de calor para realizar el trabajo: Es imposible en cualquier sistema que la transferencia de calor desde un yacimiento se convierta completamente a trabajar en un proceso cíclico en el que el sistema vuelva a su estado inicial.
Un proceso cíclico devuelve un sistema, como el gas en un cilindro, a su estado original al final de cada ciclo. La mayoría de los motores térmicos, como los motores de pistón reciprocante y las turbinas giratorias, utilizan procesos cíclicos. La segunda ley, en su segunda forma, establece claramente que tales motores no pueden tener una conversión perfecta de la transferencia de calor en trabajos realizados.
Eficiencia
Un proceso cíclico devuelve al sistema su estado original al final de cada ciclo. Por definición, la energía interna U de tal sistema es la misma al principio y al final de cada ciclo, es decir,\(\mathrm{ΔU=0}\). La primera ley de la termodinámica establece que\(\mathrm{ΔU=Q−W}\), donde Q es la transferencia neta de calor durante el ciclo (\(\mathrm{W=Q_h−Q_c}\)) y W es el trabajo neto realizado por el sistema. Ya que\(\mathrm{ΔU=0}\) para un ciclo completo, tenemos\(\mathrm{W=Q}\). Así, el trabajo neto realizado por el sistema equivale a la transferencia neta de calor al sistema, o
\(\mathrm{W=Q_h−Q_c}\)(proceso cíclico),
tal como se muestra esquemáticamente en (b).
La eficiencia es uno de los parámetros más importantes para cualquier motor térmico. El problema es que en todos los procesos, hay una transferencia de calor significativa Q c perdida al medio ambiente. En la conversión de la energía al trabajo, siempre nos encontramos ante el problema de sacar menos de lo que metemos. Definimos la eficiencia de un motor térmico (Eff) como su producción neta de trabajo W dividida por transferencia de calor al motor Q h:
\[\mathrm{E_{ff}=WQ_h.}\]
Ya que\(\mathrm{W=Q_h−Q_c}\) en un proceso cíclico, también podemos expresarlo como
\(\mathrm{Eff=\frac{Q_h−Q_c}{Q_h}=1−\frac{Q_c}{Q_h}}\)(para proceso cíclico),
dejando claro que una eficiencia de 1, o 100%, sólo es posible si no hay transferencia de calor al ambiente (Q c =0).
Ciclos de Carnot
El ciclo Carnot es el proceso cíclico más eficiente posible y utiliza solo procesos reversibles a través de su ciclo.
objetivos de aprendizaje
- Analiza por qué el motor Carnot es considerado el motor perfecto
Sabemos por la segunda ley de la termodinámica que un motor térmico no puede ser 100 por ciento eficiente, ya que siempre debe haber alguna transferencia de calor Q c al medio ambiente. (Vea nuestro átomo en “Motores de Calor “.) ¿Qué tan eficiente puede ser entonces un motor térmico? Esta pregunta fue respondida a nivel teórico en 1824 por un joven ingeniero francés, Sadi Carnot (1796-1832), en su estudio de la entonces emergente tecnología de motores térmicos cruciales para la Revolución Industrial. Ideó un ciclo teórico, ahora llamado el ciclo Carnot, que es el proceso cíclico más eficiente posible. La segunda ley de la termodinámica se puede reafirmar en términos del ciclo Carnot, y así lo que Carnot descubrió realmente fue esta ley fundamental. Cualquier motor térmico que emplee el ciclo Carnot se denomina motor Carnot.
Lo crucial para el ciclo Carnot es que solo se utilicen procesos reversibles. Los procesos irreversibles involucran factores disipativos, como la fricción y la turbulencia. Esto aumenta la transferencia de calor Qc al ambiente y reduce la eficiencia del motor. Obviamente, entonces, los procesos reversibles son superiores.
La segunda ley de la termodinámica (una tercera forma): Un motor Carnot que opera entre dos temperaturas dadas tiene la mayor eficiencia posible de cualquier motor térmico que opere entre estas dos temperaturas. Además, todos los motores que emplean solo procesos reversibles tienen esta misma eficiencia máxima cuando operan entre las mismas temperaturas dadas.
Eficiencia
El ciclo Carnot comprende dos procesos isotérmicos y dos adiabáticos. Recordemos que tanto los procesos isotérmicos como los adiabáticos son, en principio, reversibles.

Diagrama PV para un Ciclo Carnot: Diagrama PV para un ciclo Carnot, empleando solo procesos reversibles isotérmicos y adiabáticos. La transferencia de calor Qh ocurre dentro de la sustancia de trabajo durante la trayectoria isotérmica AB, la cual tiene lugar a temperatura constante Th. La transferencia de calor Qc ocurre fuera de la sustancia de trabajo durante la trayectoria isotérmica CD, la cual tiene lugar a temperatura constante Tc. La salida neta de trabajo W es igual al área dentro de la trayectoria ABCDA. También se muestra un esquema de un motor Carnot que opera entre depósitos fríos y calientes a temperaturas Th y Tc.
Carnot también determinó la eficiencia de un motor térmico perfecto, es decir, un motor Carnot. Siempre es cierto que la eficiencia de un motor térmico cíclico viene dada por:\(\mathrm{Eff=\frac{Q_h−Q_c}{Q_h}=1−\frac{Q_c}{Q_h}}\).
Lo que encontró Carnot fue que para un motor de calor perfecto, la relación\(\mathrm{\frac{Q_c}{Q_h}}}\) es igual a la relación de las temperaturas absolutas de los depósitos de calor. Es decir,\(\mathrm{\frac{Q_c}{Q_h} = \frac{T_c}{T_h}}\) para un motor Carnot, para que la eficiencia máxima o Carnot Eff C esté dada por\(\mathrm{Eff_c=1−\frac{T_c}{T_h}}\), donde T h y T c están en kelvin. (La derivación de la fórmula está ligeramente más allá del alcance de este átomo.) Ningún motor de calor real puede funcionar tan bien como la eficiencia de Carnot; una eficiencia real de aproximadamente 0.7 de este máximo suele ser la mejor que se puede lograr.
Bombas de Calor y Refrigeradores
Una bomba de calor es un dispositivo que transfiere energía térmica de una fuente de calor a un disipador de calor contra un gradiente de temperatura.
objetivos de aprendizaje
- Explicar cómo los componentes de una bomba de calor hacen que el calor se transfiera de un depósito frío a un depósito caliente
Las bombas de calor, los aires acondicionados y los refrigeradores utilizan la transferencia de calor de frío a caliente. La transferencia de calor (Q c) ocurre desde un depósito frío y hacia uno caliente. Esto requiere entrada de trabajo W, que también se convierte en transferencia de calor. Por lo tanto, la transferencia de calor al reservorio caliente es Q h =Q c +W. La misión de una bomba de calor es que la transferencia de calor Q h ocurra a un ambiente cálido, como un hogar en invierno. La misión de los aires acondicionados y refrigeradores es que la transferencia de calor Q c se produzca desde un ambiente fresco, como enfriar una habitación o mantener los alimentos a temperaturas más bajas que el ambiente. En realidad, una bomba de calor se puede utilizar tanto para calentar como para enfriar un espacio. Es esencialmente un acondicionador de aire y una unidad de calefacción todo en uno. En esta sección nos concentraremos en su modo de calentamiento.
Bombas de Calor
Un fluido de trabajo tal como un refrigerante sin CFC se usa en una bomba de calor básica. Los componentes básicos de una bomba de calor son un condensador, una válvula de expansión, un evaporador y un compresor. En los serpentines exteriores (el evaporador), la transferencia de calor Q c se produce al fluido de trabajo desde el aire frío del exterior, convirtiéndolo en un gas. El compresor accionado eléctricamente (entrada de trabajo W) eleva la temperatura y presión del gas y lo fuerza a las bobinas del condensador que están dentro del espacio calentado. Debido a que la temperatura del gas es mayor que la temperatura dentro de la habitación, se produce la transferencia de calor a la habitación y el gas se condensa en un líquido. Luego, el líquido fluye de regreso a través de una válvula reductora de presión a las bobinas del evaporador exterior, enfriándose por expansión. (En un ciclo de enfriamiento, los serpentines del evaporador y del condensador intercambian funciones y se invierte la dirección del flujo del fluido).

Bomba de calor simple: Una bomba de calor simple tiene cuatro componentes básicos: (1) condensador, (2) válvula de expansión, (3) evaporador y (4) compresor.
Coeficiente de desempeño
La calidad de una bomba de calor se juzga por la cantidad de transferencia de calor Q h que se produce al espacio cálido en comparación con la cantidad de entrada de trabajo W que se requiere. Definimos el coeficiente de rendimiento de una bomba de calor (COP hp) para ser
\[\mathrm{COP_{hp}=\dfrac{Q_h}{W}.}\]
Dado que la eficiencia de un motor térmico es Eff =W/Q h, vemos que COP hp =1/ Eff. Dado que la eficiencia de cualquier motor térmico es inferior a 1, significa que COP hp siempre es mayor que 1—es decir, una bomba de calor siempre tiene más transferencia de calor Q h que el trabajo puesto en ella. Otro punto interesante es que las bombas de calor funcionan mejor cuando las diferencias de temperatura son pequeñas. La eficiencia de un motor perfecto (o motor Carnot) es
\[\mathrm{Eff_C=1\dfrac{T_c}{T_h};}\]
así, cuanto menor sea la diferencia de temperatura, menor será la eficiencia y mayor será el COP hp.
Aires Acondicionados y Refrigeradores
Los aires acondicionados y refrigeradores están diseñados para enfriar algo en un ambiente cálido. Al igual que con las bombas de calor, se requiere entrada de trabajo para la transferencia de calor de frío a caliente. La calidad de los aires acondicionados y refrigeradores se juzga por la cantidad de transferencia de calor Q c que se produce desde un ambiente frío en comparación con la cantidad de entrada de trabajo W que se requiere. Lo que se considera el beneficio en una bomba de calor se considera calor residual en un refrigerador. Definimos así el coeficiente de rendimiento (COP ref) de un acondicionador de aire o refrigerador para ser
\[\mathrm{COP_{ref}=\dfrac{Q_c}{W}.}\]
Desde\(\mathrm{Q_h = Q_c + W}\) y\(\mathrm{COP_{hp} = \frac{Q_h}{W}}\), derivamos que
\[\mathrm{COP_{ref}=COP_{hp}−1.}\]
También, a partir de Q h >Q c, vemos que un acondicionador de aire tendrá un coeficiente de rendimiento menor que una bomba de calor.
Puntos Clave
- Muchos fenómenos termodinámicos, permitidos por la primera ley de la termodinámica, nunca ocurren en la naturaleza.
- Muchos procesos ocurren espontáneamente en una sola dirección, y la segunda ley de la termodinámica se ocupa de la dirección que toman los procesos espontáneos.
- De acuerdo con la segunda ley de la termodinámica, es imposible que cualquier proceso tenga como único resultado la transferencia de calor de un enfriador a un objeto más caliente.
- Un proceso cíclico devuelve un sistema, como el gas en un cilindro, a su estado original al final de cada ciclo. La mayoría de los motores térmicos, como los motores de pistón reciprocante y las turbinas giratorias, utilizan procesos cíclicos.
- La segunda ley de la termodinámica se puede expresar de la siguiente manera: Es imposible en cualquier sistema que la transferencia de calor desde un yacimiento se convierta completamente a trabajar en un proceso cíclico en el que el sistema regrese a su estado inicial.
- La eficiencia de un motor térmico (Eff) se define como la salida de trabajo neta del motor W dividida por la transferencia de calor al motor: EFF=WQH=1−QCQHEFF=WQH=1−QCQH, donde Q c y Q h denota transferencia de calor al depósito caliente (motor) y frío (ambiente).
- La segunda ley de termodinámica indica que un motor Carnot que opera entre dos temperaturas dadas tiene la mayor eficiencia posible de cualquier motor térmico que opere entre estas dos temperaturas.
- Los procesos irreversibles involucran factores disipativos, lo que reduce la eficiencia del motor. Obviamente, los procesos reversibles son superiores desde la perspectiva de la eficiencia.
- La eficiencia de Carnot, la máxima eficiencia del motor térmico alcanzable, se da como EFFC=1−TCTheFFC=1−Tcth.
- La misión de una bomba de calor es que la transferencia de calor Qh se produzca en un ambiente cálido, como un hogar en invierno.
- La misión de los aires acondicionados y refrigeradores es que la transferencia de calor Qc se produzca desde un ambiente fresco, como enfriar una habitación o mantener los alimentos a temperaturas más bajas que el ambiente.
- Una bomba de calor se puede utilizar tanto para calentar como para enfriar un espacio. Es esencialmente un acondicionador de aire y una unidad de calefacción todo en uno. Esto es posible al invertir el flujo de su refrigerante, cambiando la dirección neta de transferencia de calor.
Términos Clave
- entropía: Una medida de cuán uniformemente se distribuye la energía (o alguna propiedad análoga) en un sistema.
- la primera ley de la termodinámica: Una versión de la ley de conservación de la energía, especializada para sistemas termodinámicos. Generalmente se expresa como ΔU=Q−W.
- energía térmica: La energía interna de un sistema en equilibrio termodinámico debido a su temperatura.
- energía interna: La suma de toda la energía presente en el sistema, incluyendo la energía cinética y potencial; equivalentemente, la energía necesaria para crear un sistema, excluyendo la energía necesaria para desplazar su entorno.
- la segunda ley de la termodinámica: Una ley que establece que la entropía de un sistema aislado nunca disminuye, porque los sistemas aislados evolucionan espontáneamente hacia el equilibrio termodinámico, el estado de máxima entropía. Equivalentemente, las máquinas de movimiento perpetuo del segundo tipo son imposibles.
- motor térmico: Cualquier dispositivo que convierta la energía térmica en trabajo mecánico.
- CFC: Un compuesto orgánico que se utilizó comúnmente como refrigerante. Ya no se usa comúnmente debido a su efecto de agotamiento del ozono.
LICENCIAS Y ATRIBUCIONES
CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE
- Curación y Revisión. Proporcionado por: Boundless.com. Licencia: CC BY-SA: Atribución-CompartirIgual
CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA
- Colegio OpenStax, Colegio de Física. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42234/latest...ol11406/latest. Licencia: CC BY: Atribución
- la primera ley de la termodinámica. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/The%20F... termodinámica. Licencia: CC BY-SA: Atribución-CompartirIgual
- entropía. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Entropy. Licencia: CC BY-SA: Atribución-CompartirIgual
- Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42234/latest...ol11406/latest. Licencia: CC BY: Atribución
- Termodinámica y Motores Térmicos. Ubicado en: http://www.youtube.com/watch?v=I4_AfJo17qQ. Licencia: Dominio público: Sin derechos de autor conocidos. Términos de licencia: Licencia estándar de YouTube
- Colegio OpenStax, Colegio de Física. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42234/latest...ol11406/latest. Licencia: CC BY: Atribución
- Motor de calor. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Heat_Engine. Licencia: CC BY-SA: Atribución-CompartirIgual
- Sin límites. Proporcionado por: Boundless Learning. Ubicado en: www.boundless.com//fisics/de... nternal-energia. Licencia: CC BY-SA: Atribución-CompartirIgual
- Energía térmica. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Thermal_energy. Licencia: CC BY-SA: Atribución-CompartirIgual
- Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42234/latest...ol11406/latest. Licencia: CC BY: Atribución
- Termodinámica y Motores Térmicos. Ubicado en: http://www.youtube.com/watch?v=I4_AfJo17qQ. Licencia: Dominio público: Sin derechos de autor conocidos. Términos de licencia: Licencia estándar de YouTube
- Termodinámica y Motores Térmicos. Ubicado en: http://www.youtube.com/watch?v=I4_AfJo17qQ. Licencia: Dominio público: Sin derechos de autor conocidos. Términos de licencia: Licencia estándar de YouTube
- Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42234/latest...ol11406/latest. Licencia: CC BY: Atribución
- Colegio OpenStax, Colegio de Física. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42235/latest...ol11406/latest. Licencia: CC BY: Atribución
- Sin límites. Proporcionado por: Boundless Learning. Ubicado en: www.boundless.com//fisics/de... termodinámica. Licencia: CC BY-SA: Atribución-CompartirIgual
- motor de calor. Proporcionado por: Wikcionario. Ubicado en: es.wiktionary.org/wiki/heat_engine. Licencia: CC BY-SA: Atribución-CompartirIgual
- Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42234/latest...ol11406/latest. Licencia: CC BY: Atribución
- Termodinámica y Motores Térmicos. Ubicado en: http://www.youtube.com/watch?v=I4_AfJo17qQ. Licencia: Dominio público: Sin derechos de autor conocidos. Términos de licencia: Licencia estándar de YouTube
- Termodinámica y Motores Térmicos. Ubicado en: http://www.youtube.com/watch?v=I4_AfJo17qQ. Licencia: Dominio público: Sin derechos de autor conocidos. Términos de licencia: Licencia estándar de YouTube
- Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42234/latest...ol11406/latest. Licencia: CC BY: Atribución
- Colegio OpenStax, Colegio de Física. 16 de enero de 2015. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42235/latest...ol11406/latest. Licencia: CC BY: Atribución
- Colegio OpenStax, Colegio de Física. 17 de septiembre de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42236/latest...ol11406/latest. Licencia: CC BY: Atribución
- Bomba de calor. Proporcionado por: Wikipedia. Ubicado en: es.wikipedia.org/wiki/Heat_Pump. Licencia: CC BY-SA: Atribución-CompartirIgual
- Sin límites. Proporcionado por: Boundless Learning. Ubicada en: www.boundless.com//physics/de la definición/cfc. Licencia: CC BY-SA: Atribución-CompartirIgual
- Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42234/latest...ol11406/latest. Licencia: CC BY: Atribución
- Termodinámica y Motores Térmicos. Ubicado en: http://www.youtube.com/watch?v=I4_AfJo17qQ. Licencia: Dominio público: Sin derechos de autor conocidos. Términos de licencia: Licencia estándar de YouTube
- Termodinámica y Motores Térmicos. Ubicado en: http://www.youtube.com/watch?v=I4_AfJo17qQ. Licencia: Dominio público: Sin derechos de autor conocidos. Términos de licencia: Licencia estándar de YouTube
- Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42234/latest...ol11406/latest. Licencia: CC BY: Atribución
- Colegio OpenStax, Colegio de Física. 16 de enero de 2015. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42235/latest...ol11406/latest. Licencia: CC BY: Atribución
- Colegio OpenStax, Colegio de Física. 13 de febrero de 2013. Proporcionado por: OpenStax CNX. Ubicado en: http://cnx.org/content/m42236/latest...ol11406/latest. Licencia: CC BY: Atribución


