16.5: Probabilidad Termodinámica W y Entropía

La sección sobre átomos, moléculas y probabilidad ha demostrado que si queremos predecir si un cambio químico es espontáneo o no, debemos encontrar alguna manera general de determinar si el estado final es más probable que el inicial. Esto se puede hacer usando un número W, llamado probabilidad termodinámica. W se define como el número de arreglos microscópicos alternativos que corresponden al mismo estado macroscópico. La significación de esta definición se hace más evidente una vez que hemos considerado algunos ejemplos.

La Figura\(\PageIndex{1}\) a ilustra un cristal que consta de solo ocho átomos al cero absoluto de temperatura. Supongamos que la temperatura se eleva ligeramente suministrando apenas la energía suficiente para hacer vibrar uno de los átomos en el cristal. Hay ocho formas posibles de hacer esto, ya que podríamos suministrar la energía a cualquiera de los ocho átomos. Las ocho posibilidades se muestran en la Figura\(\PageIndex{1}\) b.

Figura\(\PageIndex{1}\) La probabilidad termodinámica W de un cristal que contiene ocho átomos a tres temperaturas diferentes. (a) A 0 K sólo hay una manera en la que se puede disponer el cristal, de manera que W = 1. (b) Si se agrega suficiente energía para iniciar solo uno de los átomos vibrando (color), hay ocho arreglos diferentes igualmente probables posibles, y W = 8. (c) Si la energía se duplica, dos átomos diferentes pueden vibrar simultáneamente (color claro) o un solo átomo puede tener toda la energía (color oscuro). El número de arreglos igualmente probables es mucho mayor que antes; W = 36.

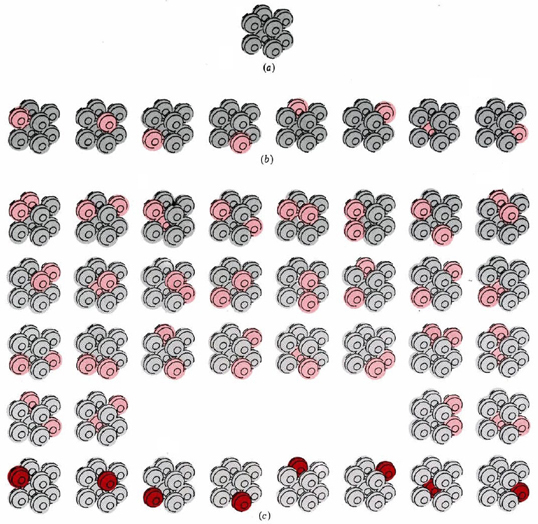
Dado que las ocho posibilidades corresponden a que el cristal tenga la misma temperatura, decimos que W = 8 para el cristal a esta temperatura. También, debemos darnos cuenta de que el cristal no se quedará perpetuamente en ninguno de estos ocho arreglos. La energía se transferirá constantemente de un átomo al otro, de manera que todos los ocho arreglos son igualmente probables.

Suministremos ahora una segunda cantidad de energía exactamente igual a la primera, para que haya justo lo suficiente para iniciar la vibración de dos moléculas. Hay 36 maneras diferentes en las que esta energía puede ser asignada a los ocho átomos (Figura\(\PageIndex{1}\) c). Decimos que W = 36 para el cristal a esta segunda temperatura. Debido a que la energía se intercambia continuamente de un átomo a otro, existe la misma probabilidad de encontrar el cristal en cualquiera de los 36 arreglos posibles.

Un tercer ejemplo de W es nuestro cristal de ocho átomos en el cero absoluto de temperatura. Dado que no hay energía para ser intercambiada de átomo a átomo, sólo es posible una disposición, y W = 1. Esto es cierto no sólo para este hipotético cristal, sino también presumiblemente para un cristal real que contiene una gran cantidad de átomos, perfectamente dispuestos, en cero absoluto.

Figura Flujo de\(\PageIndex{2}\) calor y probabilidad termodinámica. Cuando dos cristales, uno que contiene 64 unidades de energía vibratoria y el otro (a 0 K) que no contiene ninguno, las 64 unidades de energía se distribuirán sobre los dos cristales ya que hay muchas más formas de distribuir 64 unidades entre 200 átomos que hay de distribuir 64 unidades más de solo 100 átomos.

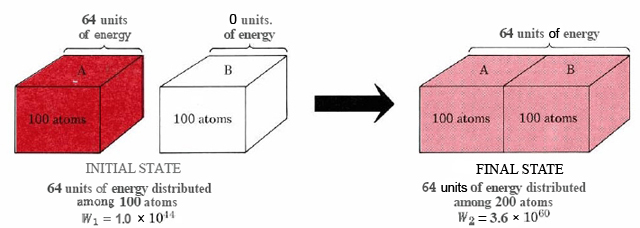
La probabilidad termodinámica W nos permite decidir cuánto más probables son ciertas situaciones que otras. Considera el flujo de calor del cristal A al cristal B, como se muestra en la Figura\(\PageIndex{2}\). Supondremos que cada cristal contiene 100 átomos. Inicialmente el cristal B está en cero absoluto. El Cristal A está a una temperatura más alta y contiene 64 unidades de energía suficiente para que 64 de los átomos vibren. Si los dos cristales se juntan, las moléculas de A pierden energía mientras que las de B ganan energía hasta que las 64 unidades de energía se distribuyen uniformemente entre ambos cristales.

En el estado inicial las 64 unidades de energía se distribuyen entre 100 átomos. Los cálculos muestran que hay 1.0 × 10 ⁴⁴ formas alternativas de hacer esta distribución. Así, W ₁, probabilidad termodinámica inicial, es 1.0× 10 ⁴⁴. Los 100 átomos del cristal A intercambian continuamente energía entre ellos y se transfieren de uno de estos arreglos de 1.0 × 10 ⁴⁴ a otro en rápida sucesión. En cualquier instante hay igual probabilidad de encontrar el cristal en cualquiera de los arreglos 1.0 × 10 ⁴⁴.

Cuando los dos cristales se ponen en contacto, la energía puede distribuirse sobre el doble de átomos. El número de arreglos posibles aumenta enormemente, y W ₂, la probabilidad termodinámica para esta nueva situación, es de 3.6 × 10 ⁶⁰. En la reorganización constante de energía entre los 200 átomos, cada uno de estos arreglos de 3.6 × 10 ⁶⁰ ocurrirá con igual probabilidad. Sin embargo, sólo 1.0 × 10 ⁴⁴ de ellos corresponden a que toda la energía esté en el cristal A. Por lo tanto, la probabilidad de que el flujo de calor se invierta y que toda la energía regrese al cristal A es

\[\frac{W_{\text{1}}}{W_{\text{2}}}=\frac{\text{1}\text{.0 }\times 10^{\text{44}}}{\text{3}\text{.6 }\times \text{ 10}^{\text{60}}}=\text{2}\text{.8 }\times \text{ 10}^{-\text{17}} \nonumber \] En otras palabras, la relación de W ₁ a W ₂ nos da la probabilidad relativa de encontrar el sistema en su estado inicial más que en su estado final.

Este ejemplo muestra cómo podemos usar W como criterio general para decidir si una reacción es espontánea o no. El movimiento de una situación molecular menos probable a una más probable corresponde al movimiento de un estado en el que W es menor a un estado donde W es mayor. En otras palabras, W aumenta para un cambio espontáneo. Si podemos encontrar alguna manera de calcular o medir los valores iniciales y finales de W, se resuelve el problema de decidir de antemano si una reacción será espontánea o no. Si W ₂ es mayor que W ₁, entonces la reacción ocurrirá por su propia cuenta. Si bien no hay nada malo en principio con este enfoque de los procesos espontáneos, en la práctica resulta ser muy engorroso. Para muestras reales de materia (a diferencia de 200 átomos en el ejemplo de la Figura 2) los valores de W son del orden de ^{10 10 24} —tan grandes que son difíciles de manipular. El logaritmo de W, sin embargo, es sólo del orden de 10 ²⁴, ya que log 10 ^x = x. Esto es más manejable, y los químicos y físicos utilizan una cantidad llamada entropía que es proporcional al logaritmo de W.

Esta forma de manejar las probabilidades termodinámicas extremadamente grandes encontradas en los sistemas reales fue sugerida por primera vez en 1877 por el físico austriaco Ludwig Boltzmann (1844 a 1906). La ecuación

\[S=k \text{ ln }W \label{2} \] ahora está grabado en la tumba de Boltzmann. La constante de proporcionalidad k se denomina, apropiadamente, la constante de Boltzmann. Corresponde a la constante de gas R dividida por la constante de Avogadro N _A: \[k=\frac{R}{N_{\text{A}}} \label{3} \] y podemos considerarla como la constante de gas por molécula en lugar de por mol. En unidades SI, la constante de Boltzmann k tiene el valor 1.3805 × 10 ^—23 J K ^—1. El símbolo ln en la Ec. \(\ref{2}\)indica un logaritmo natural, es decir, un logaritmo tomado a la base e. Dado que los logaritmos base 10 y los logaritmos base e están relacionados por la fórmula

\[\text{ln } x = 2.303 \text{ log } x \nonumber \]

es fácil de convertir de uno a otro. Ecuación\(\ref2\), expresada en logaritmos base 10, se convierte así \[S=2.303k \text{ log }W \nonumber \]

Ejemplo\(\PageIndex{1}\): Entropy

La probabilidad termodinámica W para 1 mol de gas propano a 500 K y 101.3 kPa tiene el valor 10 ^{10 25}. Calcular la entropía del gas bajo estas condiciones.

Solución Desde

\(W = 10 ^ {10^{25}}\)

\( \text{log } W = 10^{25} \)

Así\( S = 2.303k \text{ log } W = 1.3805 \times 10^{-23} \text {J K}^{-1} \times 2.303 \times 10^{25} = 318 \text{J K}^{-1} \)

Nota: La cantidad 318 J K ^—1 es obviamente mucho más fácil de manejar que 10 ^{10 25}.

Tenga en cuenta también que las dimensiones de la entropía son energía/temperatura.

Una de las propiedades de los logaritmos es que si aumentamos un número, también aumentamos el valor de su logaritmo. Por lo tanto, se deduce que si la probabilidad termodinámica W de un sistema aumenta, su entropía S debe aumentar también. Además, dado que W siempre aumenta en un cambio espontáneo, se deduce que S también debe aumentar en tal cambio.

La afirmación de que la entropía aumenta cuando se produce un cambio espontáneo se llama la segunda ley de la termodinámica. (La primera ley es la ley de conservación de la energía.) La segunda ley, como suele llamarse, es una de las leyes científicas más fundamentales y más utilizadas. En este libro solo podremos explorar algunas de sus implicaciones químicas, pero es de importancia también en los campos de la física, la ingeniería, la astronomía y la biología. Casi todos los problemas ambientales involucran la segunda ley. Siempre que la contaminación aumente, por ejemplo, podemos estar seguros de que la entropía va aumentando junto con ella.

La segunda ley se suele afirmar en términos de una diferencia de entropía Δ S. Si la entropía aumenta de un valor inicial de _S1 a un valor final de _S2 como resultado de un cambio espontáneo, entonces

\[\Delta S = S_{2} - S_{1} \label{4} \]

Dado que _S2 es mayor que _S1, podemos escribir \[\Delta S >0 \label{5} \] Ecuación nos\(\ref{5}\) dice que para cualquier proceso espontáneo, Δ S es mayor que cero. Como ejemplo de esta relación y de la posibilidad de calcular un cambio de entropía, encontremos Δ S para el caso de 1 mol de gas expandiéndose al vacío. Ya hemos argumentado para este proceso que el estado final es 10 ^{1.813 × 10 23} veces más probable que el estado inicial. Esto sólo puede ser porque hay 10 ^{1.813 × 10 23} veces más formas de lograr el estado final que el estado inicial. En otras palabras, tomando bitácoras, tenemos \[ \text{log } \frac{W_{\text{2}}}{W_{\text{1}}} = 1.813 \times 10^{23} \nonumber \] Así

\[ \begin{align} \Delta S=S_{2}-S_{1} & =2.303\times k\times \text{ log }W_{2}-2.303\times k\times \text{ log }W_{1} \\ & = 2.303 \times k \times \text{ log } \frac{W_{\text{2}}}{W_{\text{1}}} \\ & = 2.303 \times 1.3805 \times 10^{-23} \text{ J K}^{-1} \times 1.813 \times 10^{23} \end{align} \nonumber \]

\[S = 5.76 \text{J K}^{-1} \nonumber \] A medida que van los cambios de entropía, este aumento en la entropía es bastante pequeño. Sin embargo, corresponde a un cambio gigantesco en las probabilidades.