Saltar al contenido principal
LibreTexts Español

29.2: El Átomo Temprano

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    128220

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    objetivos de aprendizaje

    • Discutir experimentos que llevaron al descubrimiento del electrón y el núcleo

    Aunque originalmente se veía como una partícula que no se puede cortar en partículas más pequeñas, el uso científico moderno denota que el átomo está compuesto por varias partículas subatómicas. Las partículas constitutivas de un átomo (cada una descubierta independientemente) son: el electrón, el protón y el neutrón. (El átomo de hidrógeno-1, sin embargo, no tiene neutrones, y un ion hidrógeno positivo no tiene electrones).

    imagen

    Modelo Atómico Clásico: Modelo atómico antes de la llegada de la Mecánica Cuántica.

    Electron

    El físico alemán Johann Wilhelm Hittorf emprendió el estudio de la conductividad eléctrica en gases enrarecido. En 1869, descubrió un resplandor emitido por el cátodo que aumentaba de tamaño con la disminución de la presión del gas. En 1896, el físico británico J. J. Thomson realizó experimentos demostrando que los rayos catódicos eran partículas únicas, más que ondas, átomos o moléculas, como se creía anteriormente. Thomson hizo buenas estimaciones tanto de la carga ee como de la masa mm, encontrando que las partículas de rayos catódicos (a las que llamó “corpúsculos”) tenían quizás una milésima parte de la masa de hidrógeno, el ion menos masivo conocido. Mostró que su relación carga/masa (e/m) era independiente del material catódico. (La Fig. 1 muestra un haz de electrones desviados).

    imagen

    Haz de electrones: Un haz de electrones desviado en círculo por un campo magnético.

    Protón

    En 1917 (en experimentos reportados en 1919), Rutherford demostró que el núcleo de hidrógeno está presente en otros núcleos, resultado generalmente descrito como el descubrimiento del protón. Anteriormente, Rutherford aprendió a crear núcleos de hidrógeno como un tipo de radiación producida como un rendimiento del impacto de las partículas alfa en el gas hidrógeno; estos núcleos fueron reconocidos por su firma de penetración única en el aire y su aparición en detectores de centelleo. Estos experimentos comenzaron cuando Rutherford notó que cuando las partículas alfa se disparaban al aire (en su mayoría nitrógeno), sus detectores de centelleo mostraban las firmas de núcleos de hidrógeno típicos como producto. Después de la experimentación Rutherford rastreó la reacción al nitrógeno en el aire, y encontró que el efecto fue mayor cuando los alfas se produjeron en gas nitrógeno puro. Rutherford determinó que la única fuente posible de este hidrógeno era el nitrógeno, por lo que el nitrógeno debe contener núcleos de hidrógeno. Un núcleo de hidrógeno fue derribado por el impacto de la partícula alfa, produciendo oxígeno-17 en el proceso. Esta fue la primera reacción nuclear reportada,\(14 \mathrm { N } + \alpha \rightarrow 17 \mathrm { O } + \mathrm { p }\).

    Neutrón

    En 1920, Ernest Rutherford concibió la posible existencia del neutrón. En particular, Rutherford examinó la disparidad encontrada entre el número atómico de un átomo y su masa atómica. Su explicación para ello fue la existencia de una partícula con carga neutra dentro del núcleo atómico. Consideró que el neutrón era un doble neutro consistente en un electrón orbitando un protón. En 1932, James Chadwick mostró partículas sin carga en la radiación que utilizó. Estas partículas tenían una masa similar a los protones, pero no tenían las mismas características que los protones. Chadwick siguió algunas de las predicciones de Rutherford, la primera en trabajar en este entonces desconocido campo.

    Primeros modelos del átomo

    Dalton creía que esa materia está compuesta por unidades discretas llamadas átomos — partículas indivisibles, definitivas de materia.

    objetivos de aprendizaje

    • Describir postulados de la teoría atómica de Dalton y las teorías atómicas de los filósofos griegos antiguos

    El átomo es una unidad básica de materia que consiste en un núcleo central denso rodeado por una nube de electrones cargados negativamente. El núcleo atómico contiene una mezcla de protones cargados positivamente y neutrones eléctricamente neutros (excepto en el caso del hidrógeno-1, que es el único nucleido estable sin neutrones). Los electrones de un átomo están unidos al núcleo por la fuerza electromagnética. Tenemos un modelo detallado (y preciso) del átomo ahora, pero tardó mucho en llegar a la respuesta correcta.

    imagen

    Ilustración del átomo de helio: Esta es una ilustración del átomo de helio, que representa el núcleo (rosa) y la distribución de nubes de electrones (negro). El núcleo (superior derecha) en helio-4 es en realidad esféricamente simétrico y se asemeja mucho a la nube de electrones, aunque para núcleos más complicados no siempre es así. La barra negra es de un angstrom (10−1010−10 m, o 100pm).

    La gente ha especulado desde hace mucho tiempo sobre la estructura de la materia y la existencia de átomos. Las primeras ideas significativas en sobrevivir son de los antiguos griegos en el siglo V a.C., especialmente de los filósofos Leucipo y Demócrito. (Hay alguna evidencia de que los filósofos tanto en la India como en China hicieron especulaciones similares aproximadamente al mismo tiempo) Consideraron la cuestión de si una sustancia puede dividirse sin límite en piezas cada vez más pequeñas. Solo hay algunas respuestas posibles a esta pregunta. Una es que la subdivisión infinitesimalmente pequeña es posible. Otra es lo que Demócrito en particular creía —que hay una unidad más pequeña que no puede subdividirse aún más. Demócrito llamó a esto el átomo. Ahora sabemos que los átomos mismos pueden subdividirse, pero su identidad se destruye en el proceso, por lo que los griegos tenían razón en un aspecto. Los griegos también sentían que los átomos estaban en constante movimiento, otra noción correcta.

    Los griegos y otros especularon sobre las propiedades de los átomos, proponiendo que solo existían unos pocos tipos y que toda la materia se formaba como diversas combinaciones de estos tipos. La famosa propuesta de que los elementos básicos eran tierra, aire, fuego y agua era brillante pero incorrecta. Los griegos habían identificado los ejemplos más comunes de los cuatro estados de la materia (sólido, gas, plasma y líquido) en lugar de los elementos químicos básicos. Pasaron más de 2000 años antes de que las observaciones pudieran hacerse con equipos capaces de revelar la verdadera naturaleza de los átomos.

    A lo largo de los siglos, se hicieron descubrimientos sobre las propiedades de las sustancias y sus reacciones químicas. Se reconocieron ciertas características sistemáticas, pero las similitudes entre elementos comunes y raros dieron como resultado esfuerzos para transmutarlos (plomo en oro, en particular) para obtener ganancias financieras. El secreto era algo común. Los alquimistas descubrieron y redescubrieron muchos hechos pero no los pusieron ampliamente disponibles. Al terminar la Edad Media, la práctica de la alquimia se desvaneció gradualmente, y surgió la ciencia de la química. Ya no era posible, ni se consideraba deseable, mantener en secreto los descubrimientos. El conocimiento colectivo creció, y a principios del siglo XIX, un hecho importante estaba bien establecido: las masas de reactivos en reacciones químicas específicas siempre tienen una proporción de masa particular. Esta es una evidencia indirecta muy fuerte de que existen unidades básicas (átomos y moléculas) que tienen estas mismas proporciones de masa. El químico inglés John Dalton (1766-1844) realizó gran parte de este trabajo, con contribuciones significativas del físico italiano Amedeo Avogadro (1776-1856). Fue Avogadro quien desarrolló la idea de un número fijo de átomos y moléculas en un mol. A este número especial se le llama el número de Avogadro en su honor (\(\mathrm{6.022⋅1023}\)).

    Dalton creía que la materia está compuesta por unidades discretas llamadas átomos, a diferencia de la obsoleta noción de que la materia podría dividirse en cualquier cantidad arbitrariamente pequeña. También creía que los átomos son las partículas indivisibles y definitivas de la materia. Sin embargo, esta creencia fue anulada cerca de finales del siglo XIX por Thomson, con su descubrimiento de electrones.

    Introducción a la historia de la teoría atómica — Introducción: Rutherford, Thomson, electrones, núcleos y ciruelas. No quiero ser un bohr, pero ¿crees que el pudín debería tener un papel en la investigación científica seria?

    El modelo Thomson

    Thomson propuso que el átomo está compuesto por electrones rodeados por una sopa de carga positiva para equilibrar las cargas negativas de los electrones.

    objetivos de aprendizaje

    • Describir el modelo de un átomo propuesto por J. J. Thomson.

    J. J. Thomson, quien descubrió el electrón en 1897, propuso el modelo de pudín de ciruela del átomo en 1904 antes del descubrimiento del núcleo atómico para incluir al electrón en el modelo atómico. En el modelo de Thomson, el átomo está compuesto por electrones (que Thomson todavía llamó “corpúsculos”, aunque G. J. Stoney había propuesto que los átomos de electricidad se llamaran electrones en 1894) rodeados de una sopa de carga positiva para equilibrar las cargas negativas de los electrones, como “ciruelas” cargadas negativamente rodeadas de “pudín” cargado positivamente. Se pensaba que los electrones (como los conocemos hoy en día) estaban posicionados a lo largo del átomo en anillos giratorios. En este modelo también se describía a veces que el átomo tenía una “nube” de carga positiva.

    imagen

    Modelo de pudín de ciruela del átomo: Una presentación esquemática del modelo de pudín de ciruela del átomo; en el modelo matemático de Thomson los “corpúsculos” (en lenguaje moderno, electrones) se dispusieron de forma no aleatoria, en anillos giratorios.

    Con este modelo, Thomson abandonó su hipótesis anterior del “átomo nebular”, en la que el átomo estaba compuesto por vórtices inmateriales. Ahora bien, al menos parte del átomo iba a estar compuesto por los corpúsculos negativos particulados de Thomson, aunque el resto de la parte cargada positivamente del átomo permaneció algo nebulosa y mal definida.

    El modelo Thomson de 1904 fue refutado por el experimento de lámina de oro de 1909 realizado por Hans Geiger y Ernest Marsden. Este experimento de lámina de oro fue interpretado por Ernest Rutherford en 1911 para sugerir que hay un núcleo muy pequeño del átomo que contiene una carga positiva muy alta (en el caso del oro, suficiente para equilibrar la carga negativa colectiva de alrededor de 100 electrones). Sus conclusiones lo llevaron a proponer el modelo Rutherford del átomo.

    Introducción a la historia de la teoría atómica — El modelo Thomson: Rutherford, Thomson, electrones, núcleos y ciruelas. No quiero ser un bohr, pero ¿crees que el pudín debería tener un papel en la investigación científica seria?

    El modelo Rutherford

    Rutherford confirmó que el átomo tenía un centro concentrado de carga positiva y masa relativamente grande.

    objetivos de aprendizaje

    • Describir el experimento de lámina de oro realizado por Geiger y Marsden bajo las direcciones de Rutherford y sus implicaciones para el modelo del átomo

    El modelo de Rutherford es un modelo del átomo que lleva el nombre de Ernest Rutherford. Rutherford dirigió el famoso experimento de Geiger-Marsden en 1909, que sugería, según el análisis de Rutherford de 1911, que el llamado “modelo de pudín de ciruela” del átomo de J. J. Thomson era incorrecto. El nuevo modelo de Rutherford para el átomo, basado en los resultados experimentales, contenía las nuevas características de una carga central relativamente alta concentrada en un volumen muy pequeño en comparación con el resto del átomo. Este volumen central también contenía la mayor parte de la masa del átomo. A esta región se le llamaría más tarde el “núcleo”.

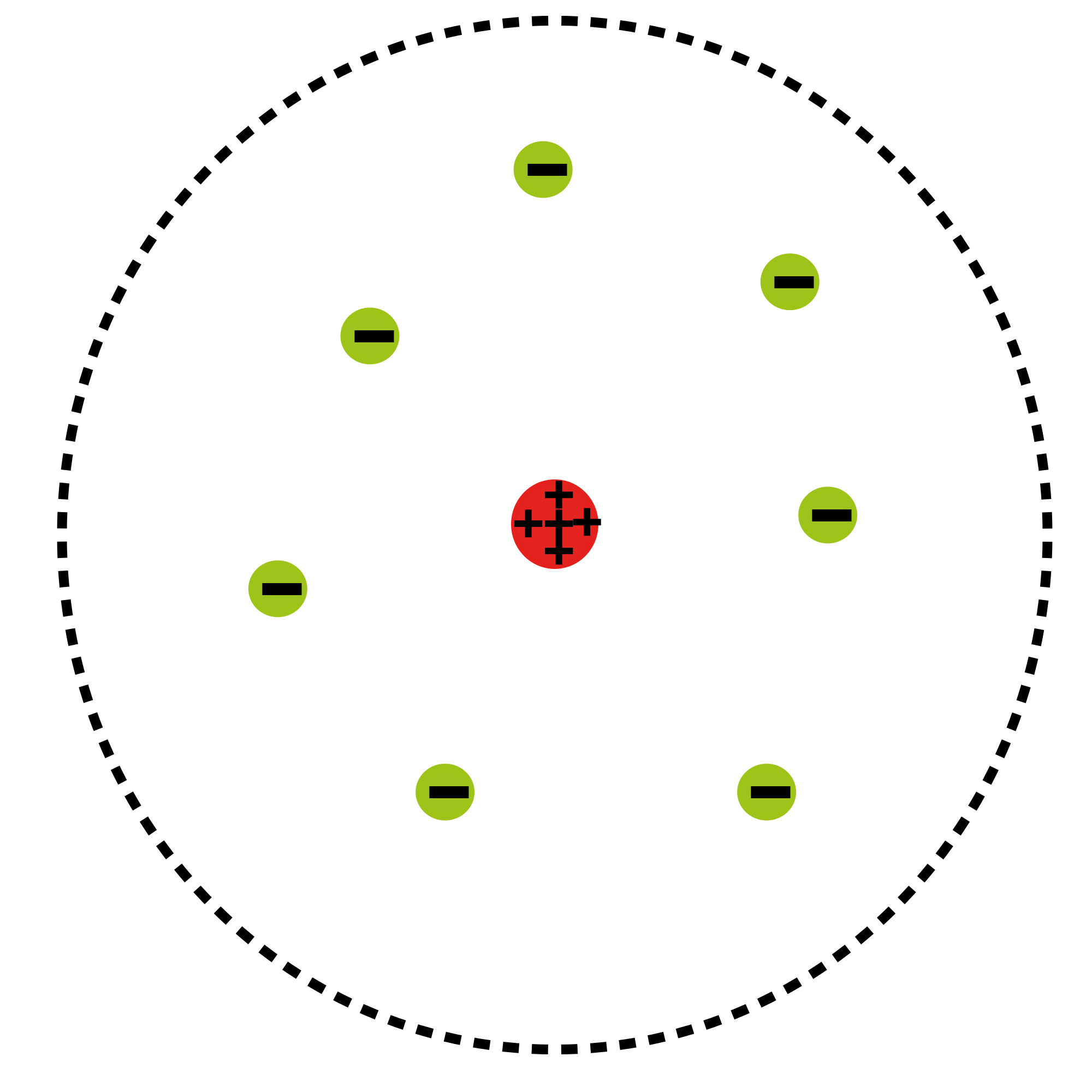
    imagen

    Modelo Planetario Atómico: Diagrama básico del modelo planetario atómico; los electrones están en verde y el núcleo está en rojo

    En 1911, Rutherford diseñó un experimento para explorar aún más la estructura atómica utilizando las partículas alfa emitidas por un elemento radiactivo. Siguiendo su dirección, Geiger y Marsden dispararon partículas alfa con grandes energías cinéticas hacia una delgada lámina de oro. Se esperaba que la medición del patrón de partículas dispersas proporcionara información sobre la distribución de la carga dentro del átomo. Bajo el modelo predominante de pudín de ciruela, todas las partículas alfa deberían haber sido desviadas, como máximo, unos pocos grados. Sin embargo, los resultados reales sorprendieron a Rutherford. Aunque muchas de las partículas alfa sí pasaron como se esperaba, muchas otras fueron desviadas en pequeños ángulos mientras que otras se reflejaron de nuevo a la fuente alfa.

    A partir de consideraciones puramente energéticas de hasta qué punto las partículas de velocidad conocida podrían penetrar hacia una carga central de 100 e, Rutherford pudo calcular que el radio de su carga central de oro tendría que ser inferior a 3.410−143.410−14 metros. Esto se encontraba en un átomo de oro conocido por tener alrededor de 10−1010−10 metros de radio; un hallazgo muy sorprendente, ya que implicaba una fuerte carga central inferior a 1300013000 th del diámetro del átomo.

    Introducción a la historia de la teoría atómica — El modelo Rutherford: Rutherford, Thomson, electrones, núcleos y ciruelas. No quiero ser un bohr, pero ¿crees que el pudín debería tener un papel en la investigación científica seria?

    El modelo Bohr del Átomo

    Bohr sugirió que los electrones en el hidrógeno podrían tener ciertos movimientos clásicos solo cuando están restringidos por una regla cuántica.

    objetivos de aprendizaje

    • Describir el modelo de átomo propuesto por Niels Bohr.

    El modelo Bohr del Átomo

    El gran físico danés Niels Bohr (1885—1962) hizo uso inmediato del modelo planetario del átomo de Rutherford. Bohr se convenció de su validez y pasó parte de 1912 en el laboratorio de Rutherford. En 1913, tras regresar a Copenhague, comenzó a publicar su teoría del átomo más simple, el hidrógeno, basada en el modelo planetario del átomo.

    imagen

    Niels Bohr: Niels Bohr, físico danés, utilizó el modelo planetario del átomo para explicar el espectro atómico y el tamaño del átomo de hidrógeno. Sus múltiples contribuciones al desarrollo de la física atómica y la mecánica cuántica; su influencia personal en muchos estudiantes y colegas; y su integridad personal, especialmente ante la opresión nazi, le valieron un lugar destacado en la historia. (crédito: Autor desconocido, vía Wikimedia Commons)

    Durante décadas, se habían hecho muchas preguntas sobre las características atómicas. Desde sus tamaños hasta sus espectros, se sabía mucho sobre los átomos, pero poco se había explicado en términos de las leyes de la física. La teoría de Bohr explicó el espectro atómico del hidrógeno, lo hizo famoso instantáneamente y estableció principios nuevos y ampliamente aplicables en la mecánica cuántica.

    Un gran acertijo que tenía el modelo planetario del átomo fue el siguiente. Las leyes de la mecánica clásica predicen que el electrón debería liberar radiación electromagnética mientras orbita un núcleo (según las ecuaciones de Maxwell, la carga acelerada debería emitir radiación electromagnética). Debido a que el electrón perdería energía, gradualmente se espiraría hacia adentro, colapsando en el núcleo. Este modelo de átomos es desastroso, porque predice que todos los átomos son inestables. Además, a medida que los electrones se hacen espirales hacia adentro, la emisión aumentaría gradualmente en frecuencia a medida que la órbita se hacía más pequeña y rápida. Esto produciría un frotis continuo, en frecuencia, de radiación electromagnética. Sin embargo, los experimentos de finales del siglo XIX con descargas eléctricas han demostrado que los átomos solo emitirán luz (es decir, radiación electromagnética) a ciertas frecuencias discretas.

    Para superar esta dificultad, Niels Bohr propuso, en 1913, lo que ahora se llama el modelo Bohr del átomo. Sugirió que los electrones solo podían tener ciertos movimientos clásicos:

    1. Los electrones en los átomos orbitan el núcleo.
    2. Los electrones sólo pueden orbitar de manera estable, sin irradiar, en ciertas órbitas (llamadas por Bohr las “órbitas estacionarias”): a cierto conjunto discreto de distancias desde el núcleo. Estas órbitas están asociadas con energías definidas y también se denominan conchas de energía o niveles de energía. En estas órbitas, la aceleración del electrón no da como resultado la pérdida de radiación y energía como lo requiere la electrodinámica clásica.
    3. Los electrones solo pueden ganar y perder energía saltando de una órbita permitida a otra, absorbiendo o emitiendo radiación electromagnética con una frecuencia νν determinada por la diferencia de energía de los niveles según la relación de Planck:

    \[\Delta \mathrm { E } = \mathrm { E } _ { 2 } - \mathrm { E } _ { 1 } = \mathrm { h } \nu\]

    donde\(\mathrm{h}\) es la constante de Planck y\(\nu\) es la frecuencia de la radiación.

    Modelo Semiclásico

    El significado del modelo de Bohr es que las leyes de la mecánica clásica se aplican al movimiento del electrón alrededor del núcleo solo cuando están restringidas por una regla cuántica. Por lo tanto, su modelo atómico se llama modelo semiclásico.

    Supuestos básicos del modelo Bohr

    Bohr explicó con éxito el espectro del hidrógeno adoptando una condición de cuantificación e introduciendo la constante de Planck en su modelo.

    objetivos de aprendizaje

    • Describir los supuestos básicos aplicados por Niels Bohr al modelo planetario de un átomo

    En módulos anteriores, hemos visto acertijos de teorías atómicas clásicas (por ejemplo, el modelo de Rutherford). Lo más importante es que la electrodinámica clásica predice que un átomo descrito por un modelo planetario (clásico) sería inestable. Para explicar el rompecabezas, Bohr propuso lo que ahora se llama el modelo Bohr del átomo en 1913. Sugirió que los electrones solo podían tener ciertos movimientos clásicos:

    1. Los electrones en los átomos orbitan el núcleo.
    2. Los electrones solo pueden orbitar de manera estable, sin irradiar, en ciertas órbitas (llamadas por Bohr las “órbitas estacionarias”) a un cierto conjunto discreto de distancias desde el núcleo. Estas órbitas están asociadas con energías definidas y también se denominan conchas de energía o niveles de energía. En estas órbitas, la aceleración del electrón no da como resultado la pérdida de radiación y energía como lo requiere la electrodinámica clásica.
    3. Los electrones solo pueden ganar y perder energía saltando de una órbita permitida a otra, absorbiendo o emitiendo radiación electromagnética con una frecuencia νν determinada por la diferencia de energía de los niveles según la relación de Planck:\(\Delta \mathrm { E } = \mathrm { E } _ { 2 } - \mathrm { E } _ { 1 } = \mathrm { h } \nu\), donde\(\mathrm{h}\) está la constante de Planck. Además, Bohr también asumió que el momento angular\(\mathrm{L}\) está restringido a ser un múltiplo entero de una unidad fija:\(\mathrm { L } = \mathrm { n } \frac { \mathrm { h } } { 2 \pi } = \mathrm { n } \hbar \), donde\(\mathrm { n } = 1,2,3 , \dots \) se llama el número cuántico principal, y\(\hbar = \frac { h } { 2 \pi }\).

    Hemos visto que Planck adoptó una nueva condición de cuantificación de energía para explicar la radiación del cuerpo negro, donde introdujo por primera vez la constante hh de Planck. Poco después, Einstein recurrió a este nuevo concepto de cuantificación de energía y volvió a utilizar la constante de Planck para explicar los efectos fotoeléctricos, en los que asumió que la radiación electromagnética interactúa con la materia como partículas (posteriormente denominadas “fotones”). Aquí, Bohr explicó con éxito el espectro de hidrógeno atómico por primera vez adoptando una condición de cuantificación e introduciendo la constante de Planck en su modelo atómico. Durante el periodo de desarrollo radical a principios del siglo XX, los físicos comenzaron a darse cuenta de que era esencial introducir la noción de “cuantificación” para explicar mundos microscópicos.

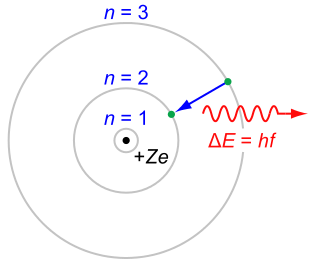
    imagen

    Modelo Rutherford-Bohr: El modelo Rutherford-Bohr del átomo de hidrógeno (\(\mathrm{Z=1}\)) o un ion similar al hidrógeno (\(\mathrm{Z>1}\)), donde el electrón cargado negativamente confinado a una capa atómica rodea un pequeño núcleo atómico cargado positivamente, y donde se acompaña un salto de electrones entre órbitas por una cantidad emitida o absorbida de energía electromagnética (hνhν). Las órbitas en las que puede viajar el electrón se muestran como círculos grises; su radio aumenta a medida que\(\mathrm{n^2}\), donde\(\mathrm{n}\) está el número cuántico principal. La\(\mathrm{3→2}\) transición aquí representada produce la primera línea de la serie Balmer, y para hidrógeno (\(\mathrm{Z=1}\)) da como resultado un fotón de longitud de onda 656 nm (luz roja).

    Órbitas de Bohr

    Según Bohr, los electrones sólo pueden orbitar de manera estable, en ciertas órbitas, a cierto conjunto discreto de distancias desde el núcleo.

    objetivos de aprendizaje

    • Explicar la relación entre las “órbitas de Bohr” y el efecto de cuantificación

    El físico danés Neils Bohr fue lo suficientemente inteligente como para descubrir un método de cálculo de las energías orbitales de electrones en hidrógeno. Como hemos visto en el módulo anterior “El modelo Bohr del átomo”, Bohr asumió que los electrones sólo pueden orbitar de manera estable, sin irradiar, en ciertas órbitas (denominadas por Bohr como “órbitas estacionarias”), a cierto conjunto discreto de distancias desde el núcleo. Estas “órbitas de Bohr” tienen una característica muy importante de cuantificación como se muestra a continuación. Este fue un primer paso importante que se ha mejorado, pero bien vale la pena repetirlo aquí, ya que describe correctamente muchas características del hidrógeno. Asumiendo órbitas circulares, Bohr propuso que se cuantifique el momento angular LL de un electrón en su órbita, es decir, solo tiene valores específicos, discretos. El valor para LL viene dado por la fórmula:

    \[\mathrm { L } = \mathrm { m } _ { \mathrm { e } } \mathrm { vr } _ { \mathrm { n } } = \mathrm { n } \dfrac { \mathrm { h } } { 2 \pi } = \mathrm { n } \hbar\]

    donde LL es el momento angular, meme es la masa del electrón, rnrn es el radio de la enésima órbita y hh es la constante de Planck. Tenga en cuenta que el momento angular es\(\mathrm { L } = \mathrm { I } \omega\). Para un objeto pequeño en un radio\(\mathrm{r, I=mr^2}\) y\(\mathrm{ω=\frac{v}{r}}\), de manera que:

    \[\mathrm { L } = \left( \mathrm { mr } ^ { 2 } \right) \left( \dfrac { \mathrm { v } } { \mathrm { r } } \right) = \mathrm { mvr }\]

    Cuantización dice que este valor de mvrmvr sólo puede tener valores discretos. En su momento, el propio Bohr no sabía por qué debía cuantificarse el momento angular, pero usando esta suposición pudo calcular las energías en el espectro de hidrógeno, algo que nadie más había hecho en ese momento.

    A continuación se muestra un diagrama de nivel de energía, que es una manera conveniente de mostrar estados de energía, los niveles de energía permitidos del electrón (en relación con nuestra discusión). La energía se traza verticalmente con el estado más bajo o fundamental en la parte inferior y con estados excitados arriba. Dadas las energías de las líneas en un espectro atómico, es posible (aunque a veces muy difícil) determinar los niveles de energía de un átomo. Los diagramas de nivel de energía se utilizan para muchos sistemas, incluyendo moléculas y núcleos. Una teoría del átomo o cualquier otro sistema debe predecir sus energías con base en la física del sistema.

    imagen

    Diagrama de nivel de energía Gráfica: Un diagrama de nivel de energía traza la energía verticalmente y es útil para visualizar los estados energéticos de un sistema y las transiciones entre ellos. Este diagrama es para los electrones de átomos de hidrógeno, mostrando una transición entre dos órbitas que tienen energías\(\mathrm{E_4}\) y\(\mathrm{E_2}\).

    Energía de una órbita de Bohr

    Con base en sus suposiciones, Bohr derivó varias propiedades importantes del átomo de hidrógeno a partir de la física clásica.

    objetivos de aprendizaje

    • Aplicar la ecuación adecuada para calcular los niveles de energía y la energía de un fotón emitido para un átomo similar al hidrógeno

    A partir de los supuestos de Bohr, ahora derivaremos una serie de propiedades importantes del átomo de hidrógeno de la física clásica. Comenzamos por señalar que la fuerza centrípeta que hace que el electrón siga una trayectoria circular es suministrada por la fuerza de Coulomb. Para ser más generales, observamos que este análisis es válido para cualquier átomo de un solo electrón. Entonces, si un núcleo tiene protones ZZ (Z=1Z=1 para hidrógeno, Z=2Z=2 para helio, etc.) y solo un electrón, ese átomo se llama átomo similar al hidrógeno.

    Los espectros de iones similares al hidrógeno son similares al hidrógeno, pero desplazados a mayor energía por la mayor fuerza de atracción entre el electrón y el núcleo. La magnitud de la fuerza centrípeta es m2evrnmev2rn, mientras que la fuerza de Coulomb es Zkee2r2Zkee2r2. La suposición tácita aquí es que el núcleo es más masivo que el electrón estacionario, y el electrón orbita alrededor de él. Esto es consistente con el modelo planetario del átomo. Equiparando estos:

    \[\dfrac { \mathrm { m } _ { \mathrm { e } } \mathrm { v } ^ { 2 } } { \mathrm { r } } = \dfrac { \mathrm { Z } \mathrm { k } _ { \mathrm { e } } \mathrm { e } ^ { 2 } } { \mathrm { r } ^ { 2 } }\]

    Esta ecuación determina la velocidad del electrón en cualquier radio:

    \[\mathrm{ v } = \dfrac { \sqrt { \mathrm{ Z k } _ { \mathrm { e } } \mathrm { e } ^ { 2 } } } { \mathrm { m } _ { \mathrm { e } } \mathrm { r } }\]

    También determina la energía total del electrón en cualquier radio:

    \[\mathrm { E } = \dfrac { 1 } { 2 } \mathrm { m } _ { \mathrm { e } } \mathrm { v } ^ { 2 } - \frac { \mathrm { Zk } _ { \mathrm { e } } \mathrm { e } ^ { 2 } } { \mathrm { r } } = - \dfrac { \mathrm { Z } \mathrm { k } _ { \mathrm { e } } \mathrm { e } ^ { 2 } } { 2 \mathrm { r } }\]

    La energía total es negativa e inversamente proporcional a rr. Esto significa que se necesita energía para alejar el electrón en órbita del protón. Para valores infinitos de rr, la energía es cero, correspondiente a un electrón inmóvil infinitamente lejos del protón.

    Ahora, aquí viene la regla cuántica: Como vimos en el módulo anterior, el momento angular L=merVL=MerV es un múltiplo entero de:

    \[\mathrm { m } _ { \mathrm { e } } \mathrm { vr } = \mathrm { n } \hbar\]

    Sustituir la expresión en la ecuación por velocidad anterior da una ecuación para rr en términos de nn:

    \[\sqrt { \mathrm { Zk } _ { \mathrm { e } } \mathrm { e } ^ { 2 } \mathrm { m } _ { \mathrm { e } } \mathrm { r } } = \mathrm { n } \hbar\]

    El radio de órbita permitido en cualquier n es entonces:

    \[\mathrm { r } _ { \mathrm { n } } = \dfrac { \mathrm { n } ^ { 2 } \hbar ^ { 2 } } { \mathrm { Zk } _ { \mathrm { e } } \mathrm { e } ^ { 2 } \mathrm { m } _ { \mathrm { e } } }\]

    El valor más pequeño posible de rr en el átomo de hidrógeno se llama radio de Bohr y es igual a 0.053 nm. La energía del enésimo nivel para cualquier átomo está determinada por el radio y el número cuántico:

    \[\mathrm { E } = - \dfrac { \mathrm { Zk } _ { \mathrm { e } } \mathrm { e } ^ { 2 } } { 2 \mathrm { r } _ { \mathrm { n } } } = - \dfrac { \mathrm { Z } ^ { 2 } \left( \mathrm { k } _ { \mathrm { e } } \mathrm { e } ^ { 2 } \right) ^ { 2 } \mathrm { m } _ { \mathrm { e } } } { 2 \hbar ^ { 2 } \mathrm { n } ^ { 2 } } \approx \dfrac { - 13.6 \mathrm { Z } ^ { 2 } } { \mathrm { n } ^ { 2 } } \mathrm { eV }\]

    Usando esta ecuación, la energía de un fotón emitido por un átomo de hidrógeno viene dada por la diferencia de dos niveles de energía de hidrógeno:

    \[\mathrm { E } = \mathrm { E } _ { \mathrm { i } } - \mathrm { E } _ { \mathrm { f } } = \mathrm { R } \left( \dfrac { 1 } { \mathrm { n } _ { \mathrm { f } } ^ { 2 } } - \dfrac { 1 } { \mathrm { n } _ { \mathrm { i } } ^ { 2 } } \right)\]

    Que es la fórmula de Rydberg que describe todo el espectro de hidrógeno y RR es la constante de Rydberg. El modelo de Bohr predijo extremadamente bien el espectro experimental de hidrógeno.

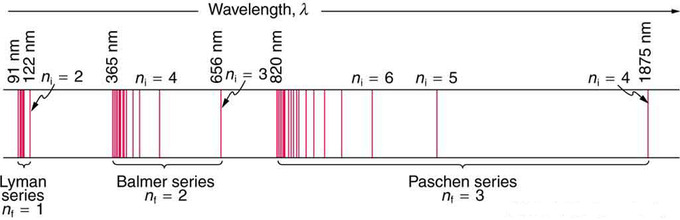
    imagen

    Fig 1: Un esquema del espectro de hidrógeno muestra varias series nombradas por aquellos que más contribuyeron a su determinación. Parte de la serie Balmer está en el espectro visible, mientras que la serie Lyman está completamente en la UV, y la serie Paschen y otras están en el IR. Los valores de nf y ni se muestran para algunas de las líneas.

    Espectros de Hidrógeno

    Las longitudes de onda observadas del espectro de hidrógeno se pueden calcular utilizando la siguiente fórmula:\(\frac { 1 } { \lambda } = \mathrm { R } \left( \frac { 1 } { \mathrm { n } _ { \mathrm { f } } ^ { 2 } } - \frac { 1 } { \mathrm { n } _ { \mathrm { i } } ^ { 2 } } \right)\).

    objetivos de aprendizaje

    • Explicar la diferencia entre las series Lyman, Balmer y Paschen

    Durante décadas, se habían hecho muchas preguntas sobre las características atómicas. Desde sus tamaños hasta sus espectros, se sabía mucho sobre los átomos, pero poco se había explicado en términos de las leyes de la física. Desde hace más de un siglo se sabe que los espectros de emisión y absorción atómicos y moleculares son discretos (o cuantificados). Maxwell y otros se habían dado cuenta de que debía haber una conexión entre el espectro de un átomo y su estructura, algo así como las frecuencias resonantes de los instrumentos musicales. Pero, a pesar de años de esfuerzos de muchas grandes mentes, nadie tenía una teoría viable. (Era una broma corriente que cualquier teoría de los espectros atómicos y moleculares podría destruirse arrojándole un libro de datos, tan complejos eran los espectros). Siguiendo la propuesta de Einstein de fotones con energías cuantificadas directamente proporcionales a sus longitudes de onda, se hizo aún más evidente que los electrones en los átomos solo pueden existir en órbitas discretas.

    En algunos casos, se habían podido idear fórmulas que describieran los espectros de emisión. Como cabría esperar, el átomo más simple, el hidrógeno, con su único electrón, tiene un espectro relativamente simple. El espectro de hidrógeno se había observado en el infrarrojo (IR), visible y ultravioleta (UV), y se habían observado varias series de líneas espectrales. Las longitudes de onda observadas del espectro de hidrógeno se pueden calcular usando la siguiente fórmula:

    \[\dfrac { 1 } { \lambda } = R \left( \dfrac { 1 } { n _ { f } ^ { 2 } } - \dfrac { 1 } { n _ { i } ^ { 2 } } \right)\]

    donde\(\mathrm{λ}\) es la longitud de onda de la radiación EM emitida y\(\mathrm{R}\) es la constante de Rydberg, determinada por el experimento a ser\(\mathrm{R=1.097⋅107 \; m^{−1}}\), y\(\mathrm{n_f, n_i}\) son números enteros positivos asociados a una serie específica.

    Estas series llevan el nombre de los primeros investigadores que las estudiaron en particular profundidad. Para la serie Lyman,\(\mathrm { n } _ { \mathrm { f } } = 1\) para la serie Balmer,\(\mathrm { n } _ { \mathrm { f } } = 2\); para la serie Paschen,\(\mathrm { n } _ { \mathrm { f } } = 3\); y así sucesivamente. La serie Lyman está completamente en la UV, mientras que parte de la serie Balmer es visible con el resto UV. La serie Paschen y todo lo demás son enteramente IR. Aparentemente hay un número ilimitado de series, aunque se encuentran progresivamente más lejos en el infrarrojo y se vuelven difíciles de observar a medida que nfnfaumenta. La constante nini es un entero positivo, pero debe ser mayor que\(\mathrm{n_f}\). Así, para la serie Balmer,\(\mathrm{n_f=2}\) y\( \mathrm { n } _ { \mathrm { i } } = 3,4,5,6 \ldots \). Tenga en cuenta que nini puede acercarse al infinito.

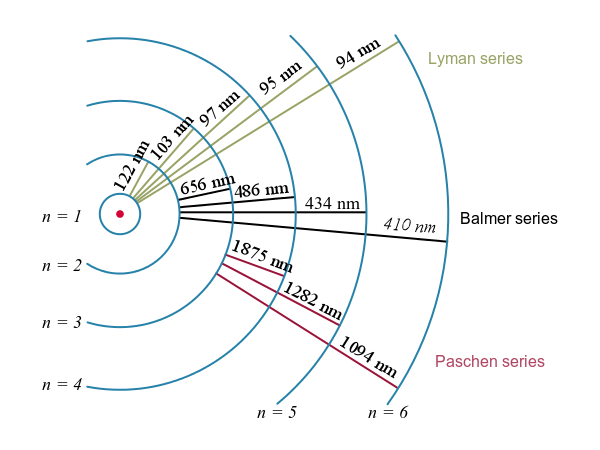
    imagen

    Transiciones de electrones y sus longitudes de onda resultantes para hidrógeno. : Los niveles de energía no están a escala.

    Si bien la fórmula en la ecuación de longitudes de onda era solo una receta diseñada para ajustarse a los datos y no se basaba en principios físicos, sí implicaba un significado más profundo. Balmer primero ideó la fórmula solo para su serie, y luego se encontró que describía todas las demás series usando diferentes valores de nfnf. Bohr fue el primero en comprender el significado más profundo. Nuevamente, vemos la interacción entre el experimento y la teoría en la física. Experimentalmente, los espectros estaban bien establecidos, se encontró una ecuación que se ajustara a los datos experimentales, pero faltó el fundamento teórico.

    de Broglie y el modelo Bohr

    Al suponer que el electrón es descrito por una onda y que debe caber un número entero de longitudes de onda, derivamos la suposición de cuantificación de Bohr.

    objetivos de aprendizaje

    • Describir la reinterpretación de la condición de Bohr por de Broglie

    La condición de Bohr, de que el momento angular es un múltiplo entero de, fue reinterpretada más tarde en 1924 por de Broglie como una condición de onda estacionaria. Las propiedades onduladas de la materia fueron confirmadas posteriormente por observaciones de interferencia electrónica cuando se dispersaron de los cristales. Los electrones solo pueden existir en lugares donde interfieran constructivamente. ¿Cómo afecta esto a los electrones en las órbitas atómicas? Cuando un electrón está unido a un átomo, su longitud de onda debe caber en un espacio pequeño, algo así como una onda estacionaria en una cuerda.

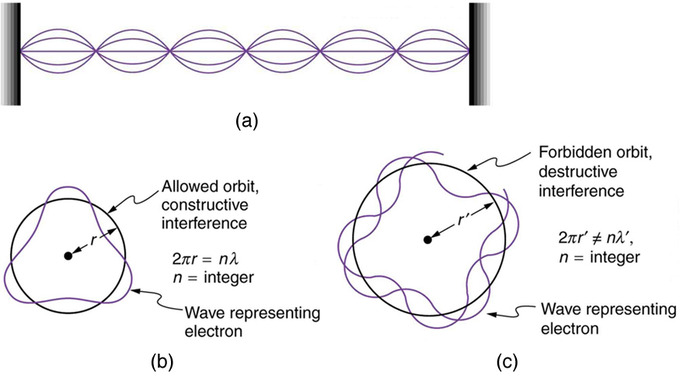
    imagen

    Ondas en una cuerda: (a) Las ondas en una cuerda tienen una longitud de onda relacionada con la longitud de la cuerda, lo que les permite interferir constructivamente. (b) Si imaginamos la cuerda doblada en un círculo cerrado, tenemos una idea aproximada de cómo los electrones en órbitas circulares pueden interferir constructivamente. c) Si la longitud de onda no encaja en la circunferencia, el electrón interfiere destructivamente; no puede existir en dicha órbita.

    Las órbitas permitidas son aquellas en las que un electrón interfiere constructivamente consigo mismo. No todas las órbitas producen interferencia constructiva y por lo tanto solo se permiten ciertas órbitas (es decir, se cuantifican las órbitas). Al suponer que el electrón es descrito por una onda y que un número entero de longitudes de onda deben caber a lo largo de la circunferencia de la órbita del electrón, tenemos la ecuación:

    \[\mathrm { n } \lambda = 2 \pi \mathrm { r }\]

    Sustituir la longitud de onda de Broglie de hphp reproduce la regla de Bohr. Desde λ=h/mevλ=h/mev, ahora tenemos:

    \[\dfrac { \mathrm { nh } } { \mathrm { m } _ { \mathrm { ev } } } = 2 \pi \mathrm { r } _ { \mathrm { n } }\]

    Reordenando términos, y señalando que L=mvrL=Mvr para una órbita circular, obtenemos la cuantificación del momento angular como condición para órbitas permitidas:

    \[\mathrm { L } = \mathrm { m } _ { \mathrm { e } } \mathrm { vr } _ { \mathrm { n } } = \mathrm { n } \frac { \mathrm { h } } { 2 \pi } , ( \mathrm { n } = 1,2,3 \dots )\]

    Como se dijo anteriormente, Bohr se vio obligado a plantear la hipótesis de esta regla para órbitas permitidas. Ahora nos damos cuenta de esto como la condición para la interferencia constructiva de un electrón en una órbita circular.

    En consecuencia, en 1925 se propuso un nuevo tipo de mecánica, la mecánica cuántica. El modelo de Bohr de electrones que viajan en órbitas cuantificadas se extendió a un modelo más preciso de movimiento de electrones. La nueva teoría fue propuesta por Werner Heisenberg. Por diferentes razonamientos, otra forma de la misma teoría, la mecánica de olas, fue descubierta independientemente por el físico austriaco Erwin Schrödinger. Schrödinger empleó las ondas de materia de Broglie, pero en su lugar buscó soluciones de onda de una ecuación de onda tridimensional. Esto describió electrones que estaban obligados a moverse alrededor del núcleo de un átomo similar al hidrógeno al ser atrapados por el potencial de la carga nuclear positiva.

    Las ondas de materia de Broglie justifican los radios orbitales mágicos de electrones de Bohr: Incluyo un resumen de la estructura electrónica del átomo de hidrógeno y explico cómo un electrón puede interferir consigo mismo en una órbita tal como lo puede hacer en un experimento de doble rendija.

    Los rayos X y el efecto Compton

    Compton explicó el cambio de frecuencia de rayos X durante la dispersión de rayos X/electrones atribuyendo el momento similar a las partículas a los “fotones”.

    objetivos de aprendizaje

    • Describir los efectos de Compton entre electrones y fotones de rayos X

    A principios del siglo XX, la investigación sobre la interacción de los rayos X con la materia estaba en marcha. Se observó que cuando los rayos X de una longitud de onda conocida interactúan con los átomos, los rayos X se dispersan a través de un ángulo θθ y emergen a una longitud de onda diferente relacionada con θθ. Aunque el electromagnetismo clásico predijo que la longitud de onda de los rayos dispersos debería ser igual a la longitud de onda inicial, múltiples experimentos habían encontrado que la longitud de onda de los rayos dispersos era más larga (correspondiente a menor energía) que la longitud de onda inicial.

    En 1923, Compton publicó un artículo en Physical Review que explicaba el cambio de rayos X atribuyendo un impulso similar a partículas a los “fotones”, que Einstein había invocado en su explicación ganadora del premio Nobel del efecto fotoeléctrico. Primero postulado por Planck, estas “partículas” conceptualizaron los elementos de luz “cuantificados” como que contenían una cantidad específica de energía dependiendo únicamente de la frecuencia de la luz. En su artículo, Compton derivó la relación matemática entre el cambio en la longitud de onda y el ángulo de dispersión de los rayos X asumiendo que cada fotón de rayos X dispersos interactuaba con un solo electrón. Su trabajo concluye informando sobre experimentos que verificaron su relación derivada:

    \[\lambda ^ { \prime } - \lambda = \dfrac { \mathrm { h } } { \mathrm { m } _ { \mathrm { e } } \mathrm { c } } ( 1 - \cos \theta ) \]

    donde λ\ lambda es la longitud de onda inicial, λ′\ lambda' es la longitud de onda después de la dispersión,\(\mathrm{h}\) es la constante de Planck,\(\mathrm{m_e}\) es la masa de reposo de electrones,\(\mathrm{c}\) es la velocidad de la luz, y θ\ theta es el ángulo de dispersión. La cantidad\(\mathrm{\frac{h}{m_e c} }\) se conoce como la longitud de onda Compton del electrón; es igual a\(\mathrm{2.43⋅10^{−12}}\) m. El desplazamiento de la longitud de onda\(\mathrm{λ‘−λ}\) es al menos cero (for\(\mathrm{θ=0°}\)) y como máximo el doble de la longitud de onda Compton del electrón (for\(\mathrm{θ=0°}\)). (La derivación de la fórmula de Compton es un poco larga y no se cubrirá aquí).

    imagen

    Un fotón que choca con un objetivo en reposo: Un fotón de longitud de onda λλ entra desde la izquierda, choca con un objetivo en reposo y un nuevo fotón de longitud de onda λ'λ' emerge en un ángulo θθ.

    Debido a que tanto la masa-energía como el impulso de un sistema deben conservarse, generalmente no es posible que el electrón simplemente se mueva en la dirección del fotón incidente. La interacción entre electrones y fotones de alta energía (comparable a la energía de reposo del electrón, 511 keV) da como resultado que el electrón recibe parte de la energía (haciéndole retroceder), y un fotón que contiene la energía restante se emite en una dirección diferente a la original, de modo que el total se conserva el impulso del sistema. Si al fotón disperso todavía le queda suficiente energía, se puede repetir el proceso de dispersión de Compton. En este escenario, el electrón es tratado como libre o libremente ligado. Los fotones con una energía de este orden de magnitud se encuentran en el rango de rayos X del espectro de radiación electromagnética. Por lo tanto, se puede decir que los efectos Compton (con electrones) ocurren con los fotones de rayos X.

    Si el fotón es de menor energía, pero aún tiene suficiente energía (en general unos pocos eV a unos pocos keV, correspondientes a la luz visible a través de rayos X suaves), puede expulsar un electrón de su átomo huésped por completo (un proceso conocido como el efecto fotoeléctrico), en lugar de sufrir dispersión de Compton. Los fotones de mayor energía (1.022 MeV y superiores, en el rango de rayos gamma) pueden bombardear el núcleo y hacer que se forme un electrón y un positrón, un proceso llamado producción de pares.

    Espectros de rayos X: orígenes, difracción por cristales e importancia

    Los rayos X muestran su naturaleza de onda cuando se irradian sobre estructuras atómicas/moleculares y se pueden utilizar para estudiarlas.

    objetivos de aprendizaje

    • Describir las interacciones entre los rayos X y los átomos

    En un átomo anterior sobre rayos X, hemos visto que hay dos procesos por los cuales se producen rayos X en el ánodo de un tubo de rayos X. En un proceso, la desaceleración de los electrones produce rayos X, y estos rayos X se llaman Bremsstrahlung, o radiación de frenado. El segundo proceso es de naturaleza atómica y produce rayos X característicos, llamados así porque son característicos del material del ánodo. El espectro de rayos X es típico de lo que produce un tubo de rayos X, mostrando una amplia curva de radiación Bremsstrahlung con picos característicos de rayos X en él.

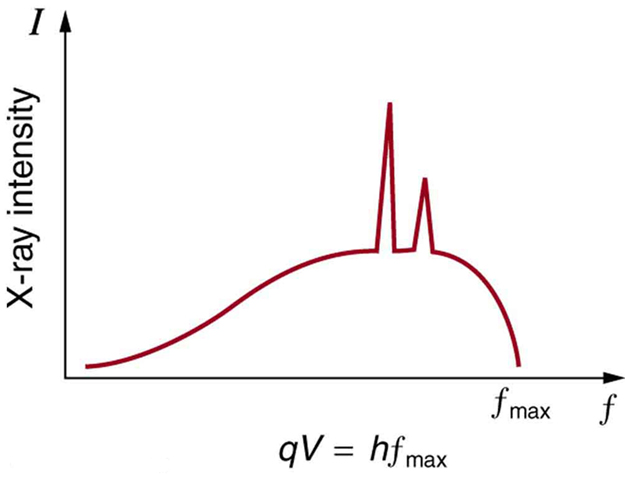
    imagen

    Espectro de rayos X: Espectro de rayos X obtenido cuando los electrones energéticos chocan con un material, como en el ánodo de un CRT. La parte lisa del espectro es la radiación bremsstrahlung, mientras que los picos son característicos del material del ánodo. Un material de ánodo diferente tendría picos de rayos X característicos a diferentes frecuencias.

    Dado que los fotones de rayos X son muy energéticos, tienen longitudes de onda relativamente cortas. Por ejemplo, la radiografía Kα de 54.4-keV, por ejemplo, tiene una longitud de onda\(\lambda = \frac { \mathrm { hc } } { \mathrm { E } } = 0.0228 \) nm. Así, los fotones típicos de rayos X actúan como rayos cuando se encuentran con objetos macroscópicos, como dientes, y producen sombras nítidas. Sin embargo, dado que los átomos y las estructuras atómicas tienen un tamaño típico del orden de 0.1 nm, los rayos X muestran su naturaleza de onda con ellos. El proceso se llama difracción de rayos X porque implica la difracción e interferencia de rayos X para producir patrones que pueden ser analizados para obtener información sobre las estructuras que dispersaron los rayos X.

    A continuación se muestra, la Ley de Bragg da los ángulos para una dispersión coherente e incoherente de la luz de una red cristalina, lo que ocurre durante la difracción de rayos X. Cuando los rayos X inciden sobre un átomo, hacen que la nube electrónica se mueva como una onda electromagnética. El movimiento de estas cargas re-irradia ondas con la misma frecuencia. Esto se llama Rayleigh Scattering, que debes recordar de un átomo anterior. Algo similar sucede cuando las ondas de neutrones de los núcleos se dispersan por la interacción con un electrón desapareado. Estos campos de onda reemitidos interfieren entre sí de manera constructiva o destructiva, y producen un patrón de difracción que es capturado por un sensor o película. Esto se llama la difracción de Braggs, y es la base para la difracción de rayos X.

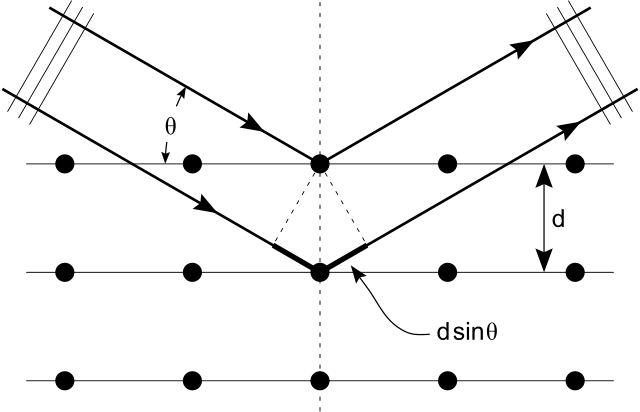
    imagen

    Difracción de rayos X: Ley de difracción de Bragg: ilustración de cómo los rayos X interactúan con la red cristalina.

    Quizás el ejemplo más famoso de difracción de rayos X es el descubrimiento de la estructura de doble hélice del ADN en 1953. Utilizando datos de difracción de rayos X, los investigadores pudieron discernir la estructura del ADN muestra un patrón de difracción producido por la dispersión de rayos X de un cristal de proteína. Este proceso se conoce como cristalografía de rayos X debido a la información que puede producir sobre la estructura cristalina. Los rayos X no solo confirman el tamaño y la forma de los átomos, sino que también dan información sobre las disposiciones atómicas en los materiales. Por ejemplo, la investigación actual en superconductores de alta temperatura involucra materiales complejos cuyas disposiciones de celosía son cruciales para obtener un material superconductor. Estos pueden ser estudiados mediante cristalografía de rayos X.

    imagen

    Difracción de rayos X: la difracción de rayos X del cristal de una proteína, lisozima de huevo de gallina, produjo este patrón de interferencia. El análisis del patrón arroja información sobre la estructura de la proteína.

    El efecto Compton

    El Efecto Compton es el fenómeno de la disminución de la energía del fotón cuando se dispersa por una partícula de carga libre.

    objetivos de aprendizaje

    • Explique por qué la dispersión de Compton es una dispersión inelástica.

    La dispersión de Compton es una dispersión inelástica de un fotón por una partícula de carga libre (generalmente un electrón). Se traduce en una disminución de la energía (aumento de la longitud de onda) del fotón (que puede ser un fotón de rayos X o rayos gamma), llamado Efecto Compton. Parte de la energía del fotón se transfiere al electrón de dispersión. La dispersión inversa de Compton también existe, y ocurre cuando una partícula cargada transfiere parte de su energía a un fotón.

    imagen

    Dispersión en el Efecto Compton: El Efecto Compton es el nombre que se le da a la dispersión de un fotón por un electrón. La energía y el impulso se conservan, resultando en una reducción de ambos para el fotón disperso. Al estudiar este efecto, Compton verificó que los fotones tienen impulso.

    La dispersión Compton es un ejemplo de dispersión inelástica porque la longitud de onda de la luz dispersada es diferente de la radiación incidente. Aún así, el origen del efecto puede considerarse como una colisión elástica entre un fotón y un electrón. La cantidad de cambio en la longitud de onda se denomina desplazamiento Compton. Aunque existe dispersión nuclear de Compton, la dispersión de Compton generalmente se refiere a la interacción que involucra solo los electrones de un átomo.

    El efecto Compton es importante porque demuestra que la luz no puede explicarse puramente como un fenómeno de onda. La dispersión de Thomson, la teoría clásica de una onda electromagnética dispersada por partículas cargadas, no puede explicar los cambios de baja intensidad en la longitud de onda: clásicamente, la luz de intensidad suficiente para que el campo eléctrico acelere una partícula cargada a una velocidad relativista provocará un retroceso de radiación-presión y un desplazamiento Doppler asociado de la luz dispersada. Sin embargo, el efecto se volverá arbitrariamente pequeño a intensidades de luz suficientemente bajas independientemente de la longitud de onda. La luz debe comportarse como si estuviera constituida por partículas para explicar la dispersión de Compton de baja intensidad. El experimento de Compton convenció a los físicos de que la luz puede comportarse como una corriente de objetos parecidos a partículas (cuantos) cuya energía es proporcional a la frecuencia.

    Puntos Clave

    • El físico británico J. J. Thomson realizó experimentos estudiando los rayos catódicos y descubrió que eran partículas únicas, posteriormente denominadas electrones.
    • Rutherford demostró que el núcleo de hidrógeno está presente en otros núcleos.
    • En 1932, James Chadwick demostró que había partículas sin carga en la radiación que estaba usando. Estas partículas, más tarde llamadas neutrones, tenían una masa similar de los protones pero no tenían las mismas características que los protones.
    • El átomo es una unidad básica de materia que consiste en un núcleo central denso rodeado por una nube de electrones cargados negativamente.
    • El conocimiento disperso descubierto por los alquimistas a lo largo de la Edad Media contribuyó al descubrimiento de los átomos.
    • Dalton estableció su teoría atómica basada en el hecho de que las masas de reactivos en reacciones químicas específicas siempre tienen una relación de masa particular.
    • J. J. Thomson, quien descubrió el electrón en 1897, propuso el modelo de pudín de ciruela del átomo en 1904 antes del descubrimiento del núcleo atómico para incluir al electrón en el modelo atómico.
    • En el modelo de Thomson, el átomo está compuesto por electrones rodeados por una sopa de carga positiva para equilibrar las cargas negativas de los electrones, como “ciruelas” cargadas negativamente rodeadas de “pudín” cargado positivamente.
    • El modelo Thomson de 1904 fue desmentido por el experimento de lámina de oro de 1909 de Hans Geiger y Ernest Marsden.
    • Rutherford volcó el modelo de Thomson en 1911 con su conocido experimento de lámina de oro, en el que demostró que el átomo tiene un núcleo minúsculo y de alta masa.
    • En su experimento, Rutherford observó que muchas partículas alfa se desviaban en pequeños ángulos mientras que otras se reflejaban de nuevo a la fuente alfa.
    • Esta región altamente concentrada y cargada positivamente se denomina “núcleo” del átomo.
    • Según Bohr: 1) Los electrones en los átomos orbitan el núcleo, 2) Los electrones sólo pueden orbitar de manera estable, sin irradiar, en ciertas órbitas, y 3) Los electrones sólo pueden ganar y perder energía saltando de una órbita permitida a otra.
    • El significado del modelo de Bohr es que las leyes de la mecánica clásica se aplican al movimiento del electrón alrededor del núcleo solo cuando están restringidas por una regla cuántica. Por lo tanto, su modelo atómico se llama modelo semiclásico.
    • Las leyes de la mecánica clásica predicen que el electrón debería liberar radiación electromagnética mientras orbita un núcleo, ¡sugiriendo que todos los átomos deberían ser inestables!
    • La electrodinámica clásica predice que un átomo descrito por un modelo planetario (clásico) sería inestable.
    • Para explicar el espectro de hidrógeno, Bohr tuvo que hacer algunas suposiciones de que los electrones solo podían tener ciertos movimientos clásicos.
    • Después del trabajo seminal de Planck, Einstein y Bohr, los físicos comenzaron a darse cuenta de que era esencial introducir la noción de “cuantificación” para explicar mundos microscópicos.
    • Las “órbitas de Bohr” tienen una característica muy importante de cuantificación: que se cuantifica el momento angular L de un electrón en su órbita, es decir, solo tiene valores específicos, discretos. Esto lleva a la ecuación\(\mathrm { L } = \mathrm { m } _ { \mathrm { e } } \mathrm { vr } _ { \mathrm { n } } = \mathrm { n } \frac { \mathrm { h } } { 2 \pi } = \mathrm { n } \hbar \).
    • Al momento de la propuesta, el propio Bohr no sabía por qué se debía cuantificar el momento angular, pero usando esta suposición pudo calcular las energías en el espectro de hidrógeno.
    • Una teoría del átomo o cualquier otro sistema debe predecir sus energías basadas en la física del sistema, lo que el modelo de Bohr pudo hacer.
    • Según Bohr, radio de órbita permitido en cualquier\(\mathrm{n}\) es\(\mathrm { r } _ { \mathrm { n } } = \frac { \mathrm { n } ^ { 2 } h ^ { 2 } } { Z \mathrm{ k } _ { e } \mathrm { e } ^ { 2 } \mathrm { m } _ { e } }\). El valor más pequeño posible de rr en el átomo de hidrógeno se llama radio de Bohr y es igual a 0.053 nm.
    • La energía del enésimo nivel para cualquier átomo es\(\mathrm { E } = \approx \frac { - 13.6 \mathrm { Z } ^ { 2 } } { \mathrm { n } ^ { 2 } } \mathrm { eV }\).
    • La energía de un fotón emitido por un átomo de hidrógeno viene dada por la diferencia de dos niveles de energía de hidrógeno:\(\mathrm { E } = \mathrm { E } _ { \mathrm { i } } - \mathrm { E } _ { \mathrm { f } } = \mathrm { R } \left( \frac { 1 } { \mathrm { n } _ { \mathrm { f } } ^ { 2 } } - \frac { 1 } { \mathrm { n } _ { \mathrm { i } } ^ { 2 } } \right) \), que se conoce como fórmula de Rydberg.
    • Desde hace más de un siglo se sabe que los espectros de emisión y absorción atómicos y moleculares son discretos (o cuantificados).
    • Las series de Lyman, Balmer y Paschen llevan el nombre de los primeros investigadores que las estudiaron en particular profundidad.
    • Bohr fue el primero en proporcionar una explicación teórica de los espectros de hidrógeno.
    • La condición de Bohr, de que el momento angular es un múltiplo entero de, fue reinterpretada más tarde en 1924 por de Broglie como una condición de onda estacionaria.
    • Por lo que Bohr se vio obligado a plantear hipótesis como regla para órbitas permitidas, el concepto de onda de materia de de Broglie lo explica como la condición para la interferencia constructiva de un electrón en una órbita circular.
    • El modelo de Bohr solo era aplicable a átomos similares a hidrógeno. En 1925 surgieron formas de descripción más generales (ahora llamadas mecánica cuántica), gracias a Heisenberg y Schrodinger.
    • Compton derivó la relación matemática entre el cambio en la longitud de onda y el ángulo de dispersión de los rayos X.
    • Los efectos de Compton (con electrones) suelen ocurrir con fotones de rayos X.
    • Si el fotón es de menor energía, en la luz visible a través del rango de rayos X suaves, se observan efectos fotoeléctricos. Los fotones de mayor energía, en el rango de rayos gamma, pueden conducir a la producción de pares.
    • Los rayos X son radiación EM de frecuencia relativamente alta. Se producen por transiciones entre niveles de electrones de capa interna, que producen rayos x característicos del elemento atómico, o acelerando electrones.
    • la difracción de rayos X es una técnica que proporciona la información detallada sobre la estructura cristalográfica de materiales naturales y manufacturados.
    • La investigación actual en ciencia de materiales y física involucra materiales complejos cuyos arreglos de celosía son cruciales para obtener un material superconductor, el cual puede ser estudiado mediante cristalografía de rayos X.

    Términos Clave

    • centelleo: Un destello de luz producido en un material transparente por el paso de una partícula.
    • partícula alfa: Núcleo cargado positivamente de un átomo de helio-4 (compuesto por dos protones y dos neutrones), emitido como consecuencia de la radiactividad.
    • cátodo: Un electrodo a través del cual fluye corriente eléctrica de un dispositivo eléctrico polarizado.
    • fuerza electromagnética: una fuerza fundamental de largo alcance que actúa entre cuerpos cargados, mediada por el intercambio de fotones
    • Número de Avogadro: el número de partículas constituyentes (generalmente átomos o moléculas) en un mol de una sustancia dada. Tiene dimensiones de mol recíproco y su valor es igual a\(6.02214129 \cdot 10^{23} \text{ mol}^{-1}\)
    • núcleo: la parte central masiva, cargada positivamente de un átomo, compuesta por protones y neutrones
    • Ecuaciones de Maxwell: Un conjunto de ecuaciones que describen cómo los campos eléctricos y magnéticos son generados y alterados entre sí y por cargas y corrientes.
    • semiclásico: una teoría en la que una parte de un sistema se describe cuánto-mecánicamente mientras que la otra se trata clásicamente.
    • cuerpo negro: Un cuerpo físico idealizado que absorbe toda la radiación electromagnética incidente, independientemente de la frecuencia o ángulo de incidencia. Si bien el cuerpo negro es un concepto teórico, se pueden encontrar realizaciones aproximadas del cuerpo negro en la naturaleza.
    • Efecto fotoeléctrico: La ocurrencia de electrones que son emitidos por la materia (metales y sólidos no metálicos, líquidos o gases) como consecuencia de su absorción de energía de la radiación electromagnética.
    • cuantización: El proceso de explicar una comprensión clásica de los fenómenos físicos en términos de una nueva comprensión conocida como mecánica cuántica.
    • centrípeta: Dirigido o moviéndose hacia un centro.
    • fotón: La cuántica de la luz y otra energía electromagnética, considerada como una partícula discreta que tiene masa de reposo cero, sin carga eléctrica, y una vida útil indefinidamente larga.
    • espectro: Una condición que no se limita a un conjunto específico de valores sino que puede variar infinitamente dentro de un continuo. La palabra vio su primer uso científico dentro del campo de la óptica para describir el arco iris de colores en luz visible cuando se separaba usando un prisma.
    • onda estacionaria: Forma de onda que se produce en un medio limitado y fijo de tal manera que la onda reflejada coincide con la onda producida. Un ejemplo común es la vibración de las cuerdas en un instrumento musical de cuerda.
    • onda de materia: Un concepto refleja la dualidad onda-partícula de la materia. La teoría fue propuesta por Louis de Broglie.
    • rayos gamma: Una radiación electromagnética de muy alta frecuencia (y por lo tanto de muy alta energía) emitida como consecuencia de la radiactividad.
    • Efectos fotoeléctricos: En los efectos fotoeléctricos, los electrones son emitidos por la materia (metales y sólidos no metálicos, líquidos o gases) como consecuencia de su absorción de energía de la radiación electromagnética.

    LICENCIAS Y ATRIBUCIONES

    CONTENIDO CON LICENCIA CC, COMPARTIDO PREVIAMENTE

    CC CONTENIDO LICENCIADO, ATRIBUCIÓN ESPECÍFICA

    29.2: El Átomo Temprano is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.