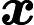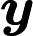13A: caída libre, también conocido como Movimiento de Proyectiles

Nota

Las ecuaciones de aceleración constante se aplican desde el primer instante en el tiempo después de que el proyectil abandona el lanzador hasta el último instante en el tiempo antes de que el proyectil golpee algo, como el suelo. Una vez que el proyectil hace contacto con el suelo, el suelo ejerce una fuerza enorme sobre el proyectil provocando un cambio drástico en la aceleración del proyectil en un periodo de tiempo muy corto hasta que, en el caso de un proyectil que no rebota, tanto la aceleración como la velocidad se vuelven cero. Tomar este valor cero de velocidad y conectarlo a ecuaciones de aceleración constante que carecen de información de aceleración posterior al contacto con el suelo es un gran error. De hecho, en ese último instante en el tiempo durante el cual aún se aplican las ecuaciones de aceleración constante, cuando el proyectil se encuentra a nivel del suelo pero aún no ha hecho contacto con el suelo, (suponiendo que el nivel del suelo es la elevación más baja alcanzada por el proyectil) la magnitud de la velocidad del proyectil está en su mayor valor, ¡tan lejos de cero como nunca llega!

Considere un objeto en caída libre con una velocidad inicial distinta de cero dirigida horizontalmente hacia adelante; o tanto hacia adelante como verticalmente (ya sea hacia arriba o hacia abajo). El objeto se moverá hacia adelante, y hacia arriba o hacia abajo —tal vez hacia arriba y luego hacia abajo— mientras continúa avanzando. En todos los casos de caída libre, el movimiento del objeto (normalmente denominado proyectil cuando se está considerando la caída libre) se realiza dentro de un solo plano vertical. Podemos definir ese plano para que sea el\(x\)\(y\) plano definiendo la dirección hacia adelante para que sea la\(x\) dirección y la dirección hacia arriba para ser la\(y\) dirección.

Una de las cosas interesantes del movimiento de proyectiles es que el movimiento horizontal es independiente del movimiento vertical. Recordemos que en caída libre, un objeto experimenta continuamente una aceleración descendente de\(9.80\dfrac{m}{s^2}\) pero no tiene aceleración horizontal. Esto significa que si disparas un proyectil para que se acerque a una pared a cierta velocidad, seguirá acercándose al muro a esa velocidad, independientemente de que también se esté moviendo hacia arriba y/o hacia abajo a medida que se acerca a la pared. Una consecuencia interesante de la independencia del movimiento vertical y horizontal es el hecho de que, descuidando la resistencia del aire, si disparas una bala horizontalmente desde, digamos, la altura de los hombros, sobre un terreno plano, y en el instante en que la bala emerge del arma, se cae una segunda bala desde la misma altura, los dos balazos golpearán el suelo al mismo tiempo. El movimiento hacia adelante de la bala disparada no afecta su movimiento vertical.

El error más común que cometen las personas al resolver problemas de movimiento de proyectiles es combinar el\(y\) movimiento\(x\) y en una ecuación estándar de aceleración constante. No hagas eso. Trate el\(x\) -motion y el\(y\) -motion por separado.

Al resolver problemas de movimiento de proyectiles, aprovechamos la independencia del\((x)\) movimiento horizontal y del\((y)\) movimiento vertical tratándolos por separado. Lo único que es común tanto al\(x\) movimiento como al\(y\) movimiento es el tiempo. La clave para la solución de muchos problemas de movimiento de proyectiles es encontrar el tiempo total de “vuelo”. Por ejemplo, considere el siguiente ejemplo.

Ejemplo\(\PageIndex{1}\)

Se lanza un proyectil con una velocidad de un\(11 m/s\) ángulo\(28^\circ\) por encima de la horizontal sobre un terreno plano desde una altura\(2.0 m\) por encima del nivel del suelo. ¿Qué tan adelante va antes de chocar contra el suelo? (Supongamos que la resistencia al aire es insignificante.)

Solución

Antes de comenzar, mejor establecemos claramente lo que se nos pide que encontremos. Definimos la dirección de avance como la\(x\) dirección así que lo que estamos buscando es un valor de\(x\). Más específicamente, estamos buscando la distancia, medida a lo largo del suelo, desde ese punto en el suelo directamente debajo del punto en el que el proyectil sale del lanzador, hasta el punto en el suelo donde golpea el proyectil. Esta distancia se conoce como el alcance del proyectil. También se conoce como el alcance del lanzador para el ángulo de lanzamiento dado y la distancia de alcance descendente recorrida por el proyectil.

Bien, ahora que sabemos para qué estamos resolviendo, comencemos. Una velocidad inicial\(28^\circ\) por encima\(11 m/s\) de la horizontal, ¿eh? ¡Ah, oh! Tenemos un dilema. La clave para resolver problemas de movimiento de proyectiles es tratar el\(x\) movimiento y el\(y\) movimiento por separado. Pero se nos da una velocidad inicial vo que es una mezcla de los dos. No tenemos más remedio que romper la velocidad inicial en su\(x\) y\(y\) componentes.

Ahora ya estamos listos para comenzar. Comenzaremos con un boceto que define nuestro sistema de coordenadas, estableciendo así el origen y las direcciones positivas para\(x\) y\(y\).

Recordemos que en los problemas de movimiento de proyectiles, tratamos el\(x\) y\(y\) movimiento por separado. Empecemos con la\(x\) moción. Es la parte más fácil porque no hay aceleración.

x movimiento

\[x=v_{ox} t\label{13-1}\]

Tenga en cuenta que para el\(x\) -motion, comenzamos con la ecuación de aceleración constante que da la posición en función del tiempo. (Imagínese haber arrancado un cronómetro en el instante en que el proyectil perdió contacto con el lanzador. La variable de tiempo t representa la lectura del cronómetro.) Como se puede ver, debido a que la aceleración en la\(x\) dirección es cero, la ecuación se simplifica rápidamente a\(x=V_{0x}t\). Estamos “atrapados” aquí porque tenemos dos incógnitas,\(x\) y\(t\), y sólo una ecuación. Es hora de recurrir a la\(y\) moción.

Debe ser evidente que es el movimiento y el que produce el tiempo, el proyectil arranca a una elevación conocida\((y = 2.0 m)\) y el movimiento del proyectil termina cuando el proyectil alcanza otra elevación conocida, a saber,\(y = 0\).

movimiento y

\[y=y_0+V_{0y}t+\dfrac{1}{2}a_yt^2 \label{13-2}\]

Esta ecuación nos dice que el\(y\) valor en cualquier momento\(t\) es el valor inicial y más algunos otros términos de los que dependen\(t\). Es válido para cualquier momento\(t\), a partir del momento del lanzamiento\(t = 0\), mientras el objeto se encuentre en movimiento de proyectil. En particular, es aplicable a ese tiempo especial\(t\), el último instante antes de que el objeto haga contacto con el suelo, ese instante que más nos interesa, el momento en que\(y = 0\). Lo que podemos hacer, es enchufar\(0\)\(y\), y resolver para ese momento especial\(t\) que, cuando se conecta a la Ecuación\(\ref{13-2}\), hace\(y\) ser\(0\). Cuando reescribimos Ecuación\(\ref{13-2}\) con y establecido en 0, el símbolo\(t\) adquiere un nuevo significado. En lugar de ser una variable, se convierte en un tiempo especial, el tiempo que hace que el\(y\) en la Ecuación real sea\(\ref{13-2}\)\((y=y=y_0+V_{0y}t+\dfrac{1}{2}a_yt^2)\) cero.

\[0=y_0+V_{0y}t_{\ast}+\dfrac{1}{2}a_yt_{\ast}^2 \label{13-3}\]

Para enfatizar que el tiempo en Ecuación\(\ref{13-3}\) es un instante particular en el tiempo más que el tiempo variable desde el lanzamiento, lo he escrito como\(t_{\ast}\) para ser leído “\(t\)estrella”. Todo en Ecuación\(\ref{13-3}\) es un dado excepto\(t_{\ast}\) así podemos resolver Ecuación\(\ref{13-3}\) para\(t_{\ast}\). Al reconocer que la ecuación\(\ref{13-3}\) es una ecuación cuadrática, primero la reescribimos en forma de la ecuación cuadrática estándar\(ax+bx^2+c=0\).\(t_{\ast}\) Esto produce:

\[\dfrac{1}{2}a_yt_{\ast}^2+V_{0y}t_{\ast}+y_0=0\]

Luego usamos la fórmula cuadrática\(x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\) que para el caso que nos ocupa aparece como:

\[t_{\ast}=\dfrac{-V_{0y}\pm\sqrt{V_{0y}^2-4(\dfrac{1}{2}a_y)y_0}}{2(\dfrac{1}{2}a_y)}\]

lo que simplifica a

\[t_{\ast}=\dfrac{-V_{0y}\pm\sqrt{V_{0y}^2-2a_yy_0}}{a_y}\]

Sustituyendo valores con rendimientos de unidades:

\[t_{\ast}=\dfrac{-4.65\dfrac{m}{s}\pm\sqrt{(-4.65\dfrac{m}{s})^2-2(-9.80\dfrac{m}{s^2})2.0m}}{-9.80\dfrac{m}{s^2}}\]

que evalúa a
\(t_{\ast}=-0.321s\) y\(t_{\ast}=1.27s\)

Descartamos la respuesta negativa porque sabemos que el proyectil choca contra el suelo después del lanzamiento, no antes del lanzamiento.

Recordemos que\(t_{\ast}\) es la lectura del cronómetro cuando el proyectil choca contra el suelo. Tenga en cuenta que todo el tiempo que ha estado moviéndose hacia arriba y hacia abajo, el proyectil ha estado avanzando de acuerdo con la Ecuación\(\ref{13-1}\),\(x=V_{0x}t\). En este punto, todo lo que tenemos que hacer es conectarnos\(t_{\ast}=1.27s\) a Ecuación\(\ref{13-1}\) y evaluar:

\[\begin{align*} x&=V_{0x}t_{\ast} \\[5pt] &=9.97\dfrac{m}{s}(1.27s) \\[5pt] &=13m \end{align*}\]

Esta es la respuesta. El proyectil viaja\(13 m\) hacia adelante antes de que golpee el suelo.