B15: Introducción al campo magnético: Efectos
- Page ID
- 129191
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Comenzamos ahora nuestro estudio del magnetismo, y, de manera análoga a la forma en que iniciamos nuestro estudio de la electricidad, comenzamos discutiendo el efecto de un campo magnético dado sin explicar primero cómo se podría hacer que existiera tal campo magnético. Ahondamos en las causas de los campos magnéticos en capítulos posteriores.
Un campo magnético es un campo vectorial. Es decir, se trata de un conjunto infinito de vectores, uno en cada punto de la región del espacio donde existe el campo magnético. Utilizamos la expresión “campo magnético” para designar tanto el conjunto infinito de vectores, como, cuando se habla del campo magnético en un punto en el espacio, el vector de campo magnético en ese punto en el espacio. Usamos el símbolo\(\vec{B}\) para representar el campo magnético. El efecto más básico de un campo magnético es ejercer un par sobre un objeto que tiene una propiedad conocida como momento dipolo magnético, y, que se encuentra en el campo magnético. Una partícula u objeto que tiene un valor distinto de cero de momento dipolo magnético se llama dipolo magnético. Un dipolo magnético es un imán de barra. El valor de la magnitud del momento dipolo magnético de un objeto es una medida de lo fuerte que es un imán de barra. Un dipolo magnético tiene dos extremos, conocidos como polos: un polo norte y un polo sur. El momento dipolo magnético es una propiedad de la materia que tiene dirección. Podemos definir la dirección, del momento dipolar magnético de un objeto, considerando que el objeto es una flecha cuyo polo norte es la punta de flecha y cuyo polo sur es la cola. La dirección en la que apunta la flecha es la dirección del momento dipolo magnético del objeto. La unidad de momento dipolo magnético es el\(A\cdot m^2\) (amperio-metro cuadrado). Si bien las agujas de brújula magnética vienen en una variedad de momentos dipolares magnéticos, un valor representativo para el momento dipolo magnético de una aguja de brújula es\(.1A\cdot m^2\).
Nuevamente, el efecto más básico de un campo magnético es ejercer un par sobre un dipolo magnético que se encuentra en el campo magnético. El vector de campo magnético, en un punto dado en el espacio, es el par máximo posible por dipolo-magnético-momente-de-aspira-ser víctima que el campo magnético ejercería/ejercerá sobre cualquier dipolo magnético (víctima) que pudiera encontrarse en el punto en cuestión. Tengo que decir “máximo posible” porque el par que se ejerce sobre el dipolo magnético depende no sólo de la magnitud del campo magnético en el punto en el espacio y la magnitud del momento dipolo magnético de la víctima, sino que también depende de la orientación del dipolo magnético con respecto a la dirección de el vector de campo magnético. De hecho:
\[\vec{\tau}=\vec{\mu}\times \vec{B}\label{15-1}\]
donde:
\(\vec{\tau}\)es el par ejercido sobre el dipolo magnético (el imán de barra) por el campo magnético,
\(\vec{\mu}\)es el momento dipolo magnético del dipolo magnético (el imán de barra, la víctima), y
\(\vec{B}\)es el vector de campo magnético en la ubicación en el espacio en el que se encuentra el dipolo magnético.
Para el producto cruzado de dos vectores cualesquiera, la magnitud del producto cruzado es el producto de las magnitudes de los dos vectores, multiplicado por el seno del ángulo que forman los dos vectores cuando se colocan cola con cola. En el caso de\(\vec{\tau}=\vec{\mu}\times \vec{B}\), esto significa:
\[\tau=\mu\space B\cos \theta\]
En el sistema SI de unidades, el par tiene unidades de\(N\cdot m\) (newton-metros). Para que las unidades del lado derecho de funcionen\(\tau=\mu\space B\cos \theta\) para ser\(N\cdot m\), lo\(\mu\) que con tener unidades de momento dipolo eléctrico (\(A\cdot m^2\)) y no\(\sin \theta\) tener unidades en absoluto,\(B\) debe tener unidades de par-por-magnetico-dipolo-momento, a saber,\(\frac{N\cdot m}{A\cdot m^2}\). A esa unidad combinada se le da nombre. Se llama tesla, abreviado\(T\).
\[1T= 1\frac{N\cdot m}{A\cdot m^2}\]
Considere un dipolo magnético que tenga un momento dipolo magnético\(\mu=0.045 \, A\cdot m^2\), oriented so that it makes an angle of \(23^{\circ}\) with the direction of a uniform magnetic field of magnitude \(5.0\times10^{-5} T\) as depicted below. Find the torque exerted on the magnetic dipole, by the magnetic field. 
Recall that the arrowhead represents the north pole of the bar magnet that a magnetic dipole is. The direction of the torque is such that it tends to cause the magnetic dipole to point in the direction of the magnetic field. For the case depicted above, that would be clockwise as viewed from the vantage point of the creator of the diagram. The magnitude of the torque for such a case can be calculated as follows:
\[\tau=\mu B\sin\theta\]
\[\tau=(.045A\cdot m^2)(5.0\times10^{-5}T)\sin 23^{\circ}\]
\[\tau=8.8\times 10^{-7} A\cdot m^2 \cdot T\]
Recalling that a tesla is a \(\frac{N\cdot m}{A\cdot m^2}\) we have:
\[\tau=8.8\times 10^{-7} A\cdot m^2 \cdot \frac{N\cdot m}{A\cdot m^2}\]
\[\tau=8.8\times 10^{-7} N\cdot m\]
Thus, the torque on the magnetic dipole is \(\tau=8.8\times 10^{-7} N\cdot m\) clockwise, as viewed from the vantage point of the creator of the diagram.
Una partícula que tiene un momento dipolar magnético\(\vec{\mu}=0.025 A\cdot m^2 \hat{i}-0.035 A\cdot m^2 \hat{j}+0.015 A\cdot m^2 \hat{k}\) is at a point in space where the magnetic field \(\vec{B}=2.3 mT \hat{i}+5.3mT\hat{j}-3.6mT\hat{k}\). Find the torque exerted on the particle by the magnetic field \[\vec{\tau}=\vec{\mu}\times \vec{B}\]
\[ \vec{\tau}=\begin{vmatrix} \hat{i}&\hat{j}&\hat{k}\\ 0.025A\cdot m^2&-0.035 A\cdot m^2&0.015 A\cdot m^2 \\ 0.0023 \frac{Nm}{Am^2} &0.0053 \frac{Nm}{Am^2} & -0.0036 \frac{Nm}{Am^2}\end{vmatrix}\]
\[\vec{\tau}=\hat{i} \Big[(-0.035Am^2)(-0.0036 \frac{Nm}{Am^2})-(0.015Am^2)(0.0053 \frac{Nm}{Am^2}) \Big]\]
\[+\hat{j} \Big[ (0.015Am^2)(0.0023 \frac{Nm}{Am^2})-(0.025Am^2)(-0.0036 \frac{Nm}{Am^2}) \Big]\]
\[+\hat{k} \Big[ (0.025Am^2)(0.0053 \frac{Nm}{Am^2})-(-0.035Am^2)(0.0023 \frac{Nm}{Am^2}) \Big]\]
\[\vec{\tau}=1.2\times10^{-4} Nm \hat{i}-1.2\times 10^{-4} Nm \hat{j}+2.1\times 10^{-4} Nm\hat{k}\]
La fuerza magnética ejercida sobre un dipolo magnético
Un campo magnético uniforme no ejerce ninguna fuerza sobre una barra magnética que se encuentra en el campo magnético. Probablemente deberías hacer una pausa aquí por un momento y dejar que eso se hunda. Un campo magnético uniforme no ejerce ninguna fuerza sobre una barra magnética que se encuentra en ese campo magnético.
Probablemente hayas tenido alguna experiencia con los imanes de barra. Ya sabes que como los polos se repelen y a diferencia de los polos atraen. Y, a partir de tu estudio del campo eléctrico, probablemente hayas planteado la hipótesis (correctamente) de que en el punto de vista del campo, la forma en que vemos esto es que un imán de barra (llamarlo imán fuente) crea un campo magnético en la región del espacio alrededor de sí mismo, y, que si hay otro imán de barra en esa región de espacio, se verá afectado por el campo magnético en el que se encuentra. Ya hemos discutido el hecho de que el imán de barra víctima experimentará un torque. Pero ya sabes, por tu experiencia con los imanes de barra, que también experimentará una fuerza. ¿Cómo puede ser eso cuando acabo de decir que un campo magnético uniforme no ejerce ninguna fuerza sobre una barra magnética? Sí, claro. El campo magnético del imán fuente debe ser no uniforme. Basta de la naturaleza del campo magnético de una barra magnética, se supone que debo guardarlo para un próximo capítulo. Baste decir que no es uniforme y centrar nuestra atención en el efecto de un campo no uniforme sobre una barra magnética que se encuentra en ese campo magnético.
En primer lugar, un campo magnético no uniforme ejercerá un par sobre un dipolo magnético (un imán de barra) igual que antes (\(\vec{\tau}=\vec{\mu}\times \vec{B}\)). Pero, un campo magnético no uniforme (uno para el cual la magnitud, y/o dirección, depende de la posición) también ejerce una fuerza sobre un dipolo magnético. La fuerza viene dada por:
\[\vec{F}_B=\nabla (\vec{\mu}\cdot \vec{B}) \label{15-2}\]
donde
- \(\vec{F}_B\)es la fuerza ejercida por el campo magnético\(\vec{B}\) sobre una partícula que tiene un momento dipolar magnético\(\vec{\tau}\)
- \(\vec{\mu}\)es el dipolo magnético de la “víctima”, y
- \(\vec{B}\)es el campo magnético en la posición en el espacio donde se encuentra la víctima. Para evaluar la fuerza, una vez\(\vec{B}\) se debe conocer en función de\(x,y\) y\(z\) (donde\(\vec{\mu}\) es una constante).
Tenga en cuenta que después de tomar el gradiente de\(\vec{\mu}\cdot \vec{B}\), hay que evaluar el resultado a los valores de\(x,y\) y\(z\) correspondientes a la ubicación de la víctima.
Solo para asegurarse de que sabe cómo usar esta ecuación, tenga en cuenta que si\(\vec{\mu}\) y\(\vec{B}\) se expresan en\(\hat{i},\hat{j},\hat{k}\) notación, para que aparezcan como\(\vec{\mu}=\mu_x \hat{i}+\mu_y \hat{j}+\mu_z \hat{k}\) y\(\vec{B}=B_x \hat{i}+B_y \hat{j}+B_z \hat{k}\) respectivamente, entonces:
\[\vec{\mu}\cdot\vec{B}=(\vec{\mu}=\mu_x \hat{i}+\mu_y \hat{j}+\mu_z \hat{k})(\vec{B}=B_x \hat{i}+B_y \hat{j}+B_z \hat{k})\]
\[\vec{\mu}\cdot\vec{B}=\mu_x B_x+\mu_y B_y+\mu_z B_z\]
Y el gradiente de\(\vec{\mu}\cdot\vec{B}\) (que por ecuación\(\ref{15-2}\) es la fuerza que buscamos) viene dado por
\[\nabla (\vec{\mu}\cdot \vec{B})=\frac{\partial (\vec{\mu}\cdot \vec{B})}{\partial x} \hat{i} +\frac{\partial (\vec{\mu}\cdot \vec{B})}{\partial y} \hat{j}+\frac{\partial (\vec{\mu}\cdot \vec{B})}{\partial z} \hat{k}\]
donde las derivadas en esta ecuación pueden (usando\(\vec{\mu}\cdot\vec{B}=\mu_x B_x+\mu_y B_y+\mu_z B_z\) desde justo arriba) se pueden expresar como:
\[\frac{\partial (\vec{\mu}\cdot\vec{B})}{\partial x}=\mu_x \frac{\partial B_x}{\partial x}+\mu_y \frac{\partial B_y}{\partial x}+\mu_z \frac{\partial B_z}{\partial x}\]
\[\frac{\partial (\vec{\mu}\cdot\vec{B})}{\partial y}=\mu_x \frac{\partial B_x}{\partial y}+\mu_y \frac{\partial B_y}{\partial y}+\mu_z \frac{\partial B_z}{\partial y}\]
\[\frac{\partial (\vec{\mu}\cdot\vec{B})}{\partial z}=\mu_x \frac{\partial B_x}{\partial z}+\mu_y \frac{\partial B_y}{\partial z}+\mu_z \frac{\partial B_z}{\partial z}\]
donde hemos aprovechado que los componentes del momento dipolo magnético de la víctima no son funciones de posición. También tenga en cuenta que los derivados son todos derivados parciales. Las derivadas parciales son del tipo fácil en el sentido de que, cuando, por ejemplo, tomas la derivada con respecto a\(x\), estás de tratar\(y\) y\(z\) como si fueran constantes. Por último, es importante darse cuenta de que, después de tomar las derivadas, hay que tapar los valores de\(x,y\) y\(z\) correspondientes a la ubicación del dipolo magnético (la víctima), en la expresión dada para la fuerza.
Existe, en una región del espacio, un campo magnético, dado en términos de vectores unitarios cartesianos por: \[\vec{B}=-5.82\times 10^{-6} T\cdot m \frac{y}{x^2+y^2} \hat{i}+5.82\times 10^{-6} T\cdot m \frac{x}{x^2+y^2} \hat{j}\]
A particle is in the region of space where the magnetic field exists. The particle has a magnetic dipole moment given by:
\[\vec{\mu}=.514A \cdot m^2 \hat{i}\]
The particle is at \((0.110m, 0, 0)\).
Find the force exerted on the particle by the magnetic field.
Solution:
First, we sketch the configuration:
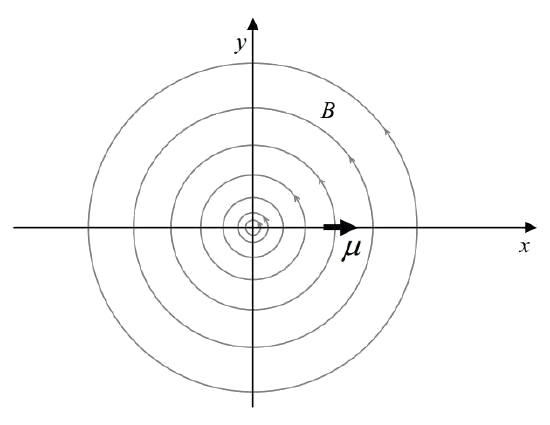
Substituting the given \(\vec{\mu}\) and \(\vec{B}\), into our expression for the force yields:
\[\vec{F}_B=\nabla (\vec{\mu}\cdot \vec{B})\]
\[\vec{F}_B=\nabla [(.514A\cdot m^2 \hat{i})\cdot (-5.82\times 10^{-6} T\cdot m \frac{y}{x^2+y^2} \hat{i}+5.82\times 10^{-6} T\cdot m \frac{x}{x^2+y^2} \hat{j})]\]
\[\vec{F}_B=\nabla \Big( -2.00\times 10^{-6} A\cdot m^2\cdot T\cdot m \frac{y}{x^2+y^2} \Big)\]
\[\vec{F}_B=-2.99\times 10^{-6} N\cdot m^2 \nabla [y(x^2+y^2)^{-1}]\]
\[\vec{F}_B=-2.99\times 10^{-6} N\cdot m^2 \Big\{ \frac{\partial}{\partial x}[y(x^2+y^2)^{-1}]\hat{i}+\frac{\partial}{\partial y}[y(x^2+y^2)^{-1}]\hat{j}+\frac{\partial}{\partial z}[y(x^2+y^2)^{-1}]\hat{k} \Big\}\]
\[\vec{F}_B=-2.99\times 10^{-6} N\cdot m^2 \{[y(-1)(x^2+y^2)^{-2} 2x\hat{i}+[(x^2+y^2)^{-1}+y(-1)(x^2+y^2)^{-2} 2y]\hat{j}+0\hat{k}\]
\[\vec{F}_B=-2.99\times 10^{-6} N\cdot m^2 \Big\{ -\frac{2xy}{(x^2+y^2)^2} \hat{i} +\Big[ \frac{1}{x^2+y^2}-\frac{2y^2}{(x^2+y^2)^2} \Big] \hat{j}\]
Recalling that we have to evaluate this expression at the location of the victim, a location that was given as \((0.110 m, 0, 0),\) we find that:
\[\vec{F}_B=-2.99\times 10^{-6} N\cdot m^2 \Big\{-\frac{2(0.110m)0}{[(0.110m^2)+0^2]^2}\hat{i}+\Big[\frac{1}{(0.110m)^2+0^2}-\frac{2(0)^2}{[(0.110m)^2+0^2]^2} \Big] \hat{j} \Big\}\]
\[\vec{F}_B=-2.47\times 10^{-4} N \hat{j}\]
Solution:
First, we sketch the configuration:
Substituting the given \(\vec{\mu}\) and \(\vec{B}\), into our expression for the force yields:
\[\vec{F}_B=\nabla (\vec{\mu}\cdot \vec{B})\]
\[\vec{F}_B=\nabla [(.514A\cdot m^2 \hat{i})\cdot (-5.82\times 10^{-6} T\cdot m \frac{y}{x^2+y^2} \hat{i}+5.82\times 10^{-6} T\cdot m \frac{x}{x^2+y^2} \hat{j})]\]
\[\vec{F}_B=\nabla \Big( -2.00\times 10^{-6} A\cdot m^2\cdot T\cdot m \frac{y}{x^2+y^2} \Big)\]
\[\vec{F}_B=-2.99\times 10^{-6} N\cdot m^2 \nabla [y(x^2+y^2)^{-1}]\]
\[\vec{F}_B=-2.99\times 10^{-6} N\cdot m^2 \Big\{ \frac{\partial}{\partial x}[y(x^2+y^2)^{-1}]\hat{i}+\frac{\partial}{\partial y}[y(x^2+y^2)^{-1}]\hat{j}+\frac{\partial}{\partial z}[y(x^2+y^2)^{-1}]\hat{k} \Big\}\]
\[\vec{F}_B=-2.99\times 10^{-6} N\cdot m^2 \{[y(-1)(x^2+y^2)^{-2} 2x\hat{i}+[(x^2+y^2)^{-1}+y(-1)(x^2+y^2)^{-2} 2y]\hat{j}+0\hat{k}\]
\[\vec{F}_B=-2.99\times 10^{-6} N\cdot m^2 \Big\{ -\frac{2xy}{(x^2+y^2)^2} \hat{i} +\Big[ \frac{1}{x^2+y^2}-\frac{2y^2}{(x^2+y^2)^2} \Big] \hat{j}\]
Recalling that we have to evaluate this expression at the location of the victim, a location that was given as \((0.110 m, 0, 0),\) we find that:
\[\vec{F}_B=-2.99\times 10^{-6} N\cdot m^2 \Big\{-\frac{2(0.110m)0}{[(0.110m^2)+0^2]^2}\hat{i}+\Big[\frac{1}{(0.110m)^2+0^2}-\frac{2(0)^2}{[(0.110m)^2+0^2]^2} \Big] \hat{j} \Big\}\]
\[\vec{F}_B=-2.47\times 10^{-4} N \hat{j}\]
Características del Campo Magnético de la Tierra
Vivimos en un campo magnético producido por la tierra. Tanto su magnitud como su dirección son diferentes en diferentes lugares de la superficie de la tierra. Además, en cualquier lugar dado, el campo magnético de la Tierra varía de un año a otro tanto en magnitud como en dirección. Aún así, en la escala geográfica de un campus universitario, y, en una escala de tiempo medida en días, el campo magnético de la tierra es aproximadamente uniforme y constante.
Para alinear el dedo índice con el campo magnético de la tierra en el campus Saint Anselm College, primer punto en dirección horizontal al\(15.4^{\circ}\) Oeste del Norte. Después inclina tu brazo hacia abajo para que estés apuntando en una dirección que esté\(68.9^{\circ}\) por debajo de la horizontal. (¡Sí! ¿Te lo puedes creer? ¡Es mayormente a la baja!) Ahora estás apuntando con el dedo en dirección al campo magnético de la tierra. La magnitud del campo magnético, en el campus Saint Anselm College, es\(5.37\times 10^{-5} T\). En otras palabras:
| Característica | Valor | Tasa de cambio |
|---|---|---|
| Declinación | \(-15.4^{\circ}\) | \(+0.074 ^{\circ}/\mbox{year}\) |
| Inclinación (ángulo de inmersión) | \(68.8^{\circ}\) | \(-0.096 ^{\circ}/\mbox{year}\) |
| Magnitud | \(5.36\times 10^{-5}T\) | \(-0.012\times 10^{-5} T/\mbox{year}\) |
| Componente Horizontal | \(1.93\times 10^{-5}T\) | \(+0.004\times 10^{-5} T/\mbox{year}\) |
| Componente Vertical | \(5.00\times 10^{-5}T\) | \(-0.014\times 10^{-5} T/\mbox{year}\) |
Una aguja de brújula es un imán de barra diminuta que está obligado a girar alrededor de un eje vertical. El campo magnético de la tierra ejerce un par sobre la aguja de la brújula que tiende a hacer que la aguja de la brújula apunte en la dirección de la componente horizontal del campo magnético terrestre, una dirección que llamamos “norte magnético”. Recordemos que cuando hablamos de a qué dirección apunta un imán de barra (como una aguja de brújula), imaginamos que hay una punta de flecha en su polo norte.


