3.1: Inercia
- Page ID
- 128264
En el lenguaje cotidiano, hablamos de algo o alguien “que tiene una gran inercia” para significar, esencialmente, que son muy difíciles de poner en marcha. Este uso de la palabra “inercia” es consistente con la “ley de inercia” que introdujimos en el capítulo anterior (que establece, entre otras cosas, que un objeto en reposo, si se deja a sí mismo, simplemente permanecerá en reposo), pero va un poco más allá de eso al tratar de cuantificar lo difícil que puede ser conseguir que el objeto muévete.
Sabemos, por experiencia, que los objetos más ligeros son más fáciles de poner en movimiento que los objetos más pesados, pero la mayoría de nosotros probablemente tenemos la intuición de que la gravedad (la fuerza que tira de un objeto hacia la tierra y por lo tanto determina su peso) no está involucrada de manera esencial aquí. Imagina, por ejemplo, la diferencia entre abofetear una pelota de voleibol y una bola de boliche. No es difícil creer que a esta última le dolería tanto si lo hiciéramos flotando en caída libre en la estación espacial (en un estado de “ingravidez” efectiva) como si lo hiciéramos aquí mismo en la superficie de la tierra. En otras palabras, no es (necesariamente) lo pesado que se siente algo, sino lo masivo que es.
Pero justo ¿cuál es esta cualidad de “masividad” que asociamos intuitivamente con una gran inercia? ¿Hay alguna manera (que no sea recurrir nuevamente al peso) de asignarle un valor numérico?
Inercia Relativa y Colisiones
Una forma posible de determinar las inercias relativas de dos objetos, conceptualmente, al menos, es intentar utilizar uno de ellos para poner en movimiento al otro. La mayoría de nosotros estamos familiarizados con lo que sucede cuando dos objetos idénticos (presumiblemente, por lo tanto, que tienen la misma inercia) chocan: si la colisión es frontal (así el movimiento, antes y después, se limita a una línea recta), básicamente intercambian velocidades. Por ejemplo, una bola de billar golpeando a otra parará muerta y la segunda partirá con la misma velocidad que la primera. El juguete a veces llamado “las bolas de Newton” o “la cuna de Newton” también muestra este efecto. Intuitivamente, entendemos que lo que se necesita para detener la primera bola es exactamente lo mismo que se necesitaría para poner la segunda en movimiento con la misma velocidad.
Pero, ¿y si los objetos que colisionan tienen diferentes inercias? Esperamos que el cambio en sus velocidades como resultado de la colisión sea diferente: la velocidad del objeto con la mayor inercia no cambiará mucho, y a la inversa, el cambio en la velocidad del objeto con la inercia más pequeña será comparativamente mayor. Un gráfico de velocidad vs. tiempo para los dos objetos podría parecerse a la esbozada en la Figura\(\PageIndex{1}\).
En esta imagen, el objeto 1, inicialmente moviéndose con velocidad\(v_{1i}\) = 1 m/s, choca con el objeto 2, inicialmente en reposo. Después de la colisión, que aquí se supone que toma aproximadamente un milisegundo, el objeto 1 realmente rebota, por lo que su velocidad final es\(v_{1f}\) = −1/3 m/s, mientras que el objeto 2 termina moviéndose hacia la derecha con una velocidad\(v_{2f}\) = 2/3 m/s Entonces el cambio en la velocidad del objeto 1 es\(\Delta v_1 = v_{1f} −v_{1i}\) = −4/3 m/s, mientras que para el objeto 2 tenemos\(\Delta v_2 = v_{2f} − v_{2i}\) = 2/3 m/s.
Es tentador usar esta relación,\(\Delta v_1/ \Delta v_2\), como medida de la inercia relativa de los dos objetos, solo queremos usarla boca abajo y con el signo opuesto: es decir, ya que\(\Delta v_2/ \Delta v_1\) = −1/2 diríamos que el objeto 2 tiene el doble de inercia del objeto 1. Pero entonces tenemos que preguntarnos: ¿es esta una medida confiable, repetible? ¿Funcionará para cualquier tipo de colisión (dentro de lo razonable, claro: claramente necesitamos permanecer en una dimensión, y eliminar influencias externas como la fricción), y para cualquier velocidad inicial?
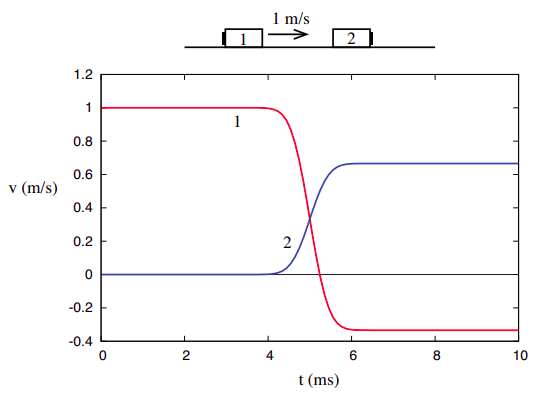
Para empezar, tenemos razones para esperar que no importa si disparamos al objeto 1 hacia el objeto 2 o al objeto 2 hacia el objeto 1, porque aprendimos en el capítulo anterior que solo el movimiento relativo es detectable, y el movimiento relativo es el mismo en ambos casos. Consideremos, por ejemplo, cómo\(\PageIndex{1}\) aparece la colisión en la Figura a un hipotético observador que se mueve junto con el objeto 1, a 1 m/s. Para él, el objeto 1 parece estar en reposo, y es el objeto 2 el que viene hacia él, con una velocidad de −1 m/s. Para ver cómo se ve el resultado de la colisión para él, solo agrega los mismos −1 m/s a las velocidades finales que obtuvimos antes: el objeto 1 acabará moviéndose a\(v_{1f}\) = −4/3 m/s, y el objeto 2 se movería a\(v_{2f}\) = −1/3 m/s, y tendríamos una situación como la que se muestra en la Figura\(\PageIndex{2}\), donde ambas curvas simplemente se han desplazado hacia abajo en 1 m/s:
Figura\(\PageIndex{2}\): Otro ejemplo (realmente la misma colisión que en la Figura\(\PageIndex{1}\), solo como lo ve un observador que inicialmente se mueve hacia la derecha a 1 m/s).
Pero entonces, esto es exactamente lo que deberíamos esperar encontrar también en nuestro laboratorio si realmente enviamos el segundo objeto a 1 m/s hacia el primero sentado en reposo. Todas las velocidades individuales han cambiado en relación con la Figura\(\PageIndex{1}\), pero la velocidad cambia,\(\Delta v_1\) y\(\Delta v_2\), claramente siguen siendo las mismas, y por lo tanto también lo es nuestra medida (tentativa) de la inercia relativa de los objetos.
Claramente, se puede usar el mismo argumento para concluir que se obtendrá el mismo resultado cuando ambos objetos se muevan inicialmente uno hacia el otro, siempre y cuando su velocidad relativa sea la misma que en estos ejemplos, es decir, 1 m/s. Sin embargo, a menos que hagamos los experimentos realmente no podemos predecir qué sucederá si aumentamos (o disminuimos) su velocidad relativa. De hecho, podríamos imaginarnos aplastando los dos objetos a muy alta velocidad, por lo que incluso podrían quedar seriamente destrozados en el proceso. Sin embargo, experimentalmente (¡y esto no es en absoluto un resultado obvio!) , todavía encontraríamos el mismo valor de −1/2 para la relación\(\Delta v_2/ \Delta v_1\), al menos siempre y cuando la colisión no sea tan violenta que los objetos realmente se rompan en pedazos.
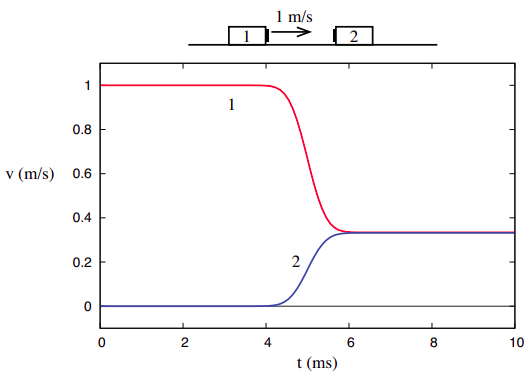
Quizás el resultado más sorprendente de nuestros experimentos sería el siguiente: imagina que los objetos tienen un lado “pegajoso” (por ejemplo, los pequeños rectángulos negros que se muestran en las imágenes podrían ser tiras de Velcro), y los volteamos para que cuando choquen terminen pegados entre sí. En este caso (que, como veremos más adelante, se denomina colisión completamente inelástica), la\(t\) gráfica\(v\) -vs- podría parecerse\(\PageIndex{3}\) a la Figura siguiente.
Ahora los dos objetos terminan moviéndose juntos hacia la derecha, bastante lentamente:\(v_{1f} = v_{2f}\) = 1/3 m/s Los cambios de velocidad son\(\Delta v_1\) = −2/3 m/s y\(\Delta v_2\) = 1/3 m/s, ambos diferentes de lo que eran antes, en las Figs. \(\PageIndex{1}\)y\(\PageIndex{2}\): sin embargo, la relación\(\Delta v_2/ \Delta v_1\) sigue siendo igual a −1/2, al igual que en todos los casos anteriores.
Masa inercial: definición y propiedades
En este punto, parecería razonable suponer que esta relación,, es\(\Delta v_2/ \Delta v_1\), de hecho, decirnos algo sobre una propiedad intrínseca de los dos objetos, lo que hemos llamado por encima de su “inercia relativa”. Es fácil, entonces, ver cómo se podría asignar un valor a la inercia de cualquier objeto (al menos, conceptualmente): elegir un objeto “estándar”, y decidir, arbitrariamente, que su inercia tendrá el valor numérico de 1, en las unidades que elija para él (estas unidades resultarán, de hecho, ser kilogramos, como tú verá en un minuto). Luego, para determinar la inercia de otro objeto, que etiquetaremos con el subíndice 1, basta con organizar una colisión unidimensional entre el objeto 1 y el estándar, bajo las condiciones adecuadas (básicamente, sin fuerzas externas netas), medir los cambios de velocidad\(\Delta v_1\) y\(\Delta v_s\), y tomar la cantidad \(−\Delta v_s/ \Delta v_1\)como el valor numérico de la relación de la inercia del objeto 1 a la inercia del objeto estándar. En símbolos, usando la letra\(m\) para representar la inercia de un objeto,
\[ \frac{m_{1}}{m_{s}}=-\frac{\Delta v_{s}}{\Delta v_{1}} \label{eq:3.1} \]
Pero, ya que\(m_s\) = 1 por definición, esto nos da directamente el valor numérico de\(m_1\).
El motivo por el que usamos la letra\(m\) es, como debiste haber adivinado, porque, de hecho, la inercia definida de esta manera resulta ser idéntica a lo que tradicionalmente hemos llamado “masa”. Más precisamente, la cantidad definida de esta manera es la masa inercial de un objeto. El hecho notable, mencionado anteriormente, de que la fuerza de gravedad entre dos objetos resulta ser proporcional a sus masas inerciales, nos permite determinar la masa inercial de un objeto mediante el procedimiento más tradicional de simplemente pesarlo, en lugar de escenificar elaboradamente una colisión entre éste y el kilogramo estándar en una pista de hockey sobre hielo. Pero, en principio, podríamos concebir la existencia de dos cantidades diferentes que deberían llamarse “masa inercial” y “masa gravitacional”, y la identidad (o más precisamente, la proporcionalidad exacta —hasta donde sepamos—) de las dos es un hecho experimental bastante misterioso 1.
En cualquier caso, por la forma en que la hemos construido, la masa inercial, definida como en la Ecuación (\ ref {eq:3.1}), sí capta, de manera cuantitativa, el concepto que estábamos tratando de expresar al inicio del capítulo: a saber, lo difícil que puede ser poner en movimiento un objeto. En principio, sin embargo, habría que realizar otros experimentos para asegurarnos de que sí tiene las propiedades que tradicionalmente hemos asociado con el concepto de masa. Por ejemplo, supongamos que unimos dos objetos de masa\(m\). ¿Es la masa del objeto resultante\(2m\)? Los experimentos de colisión, en efecto, demostrarían que este es el caso con gran precisión en el mundo macroscópico (del que nos ocupa este semestre), pero este es un buen ejemplo de cómo no se puede dar nada por sentado: a nivel microscópico, nuevamente es un hecho que la masa inercial de un núcleo atómico es un poco menor que la suma de las masas de todos sus protones y neutrones constituyentes 2.
Probablemente lo último que habría que comprobar es que la relación de inercias es independiente de la norma. Supongamos que tenemos dos objetos, a los que hemos asignado masas\(m_1\) y\(m_2\) disponiendo para que cada uno colisione con el “objeto estándar” de forma independiente. Si ahora hacemos arreglos para una colisión entre los objetos 1 y 2 directamente, ¿encontraremos realmente que la relación de sus cambios de velocidad viene dada por la relación de las masas determinadas por separado\(m_1\) y\(m_2\)? Ciertamente necesitaríamos que ese fuera el caso, para que el concepto de inercia sea verdaderamente útil; pero de nuevo, ¡no debemos asumir nada hasta que lo hayamos probado! Afortunadamente, las pruebas efectivamente revelarían que, en todos los casos, la relación esperada sostiene 3
\[ -\frac{\Delta v_{2}}{\Delta v_{1}}=\frac{m_{1}}{m_{2}} \label{eq:3.2} .\]
En este punto, no sólo estamos en posesión de una útil definición de inercia, sino también de una verdadera ley de la naturaleza, como voy a explicar a continuación.
1 Este hecho, elevado a la categoría de un principio por Einstein (el principio de equivalencia) es el punto de partida de la teoría general de la relatividad.
2 Y esto no es sólo un poco poco importante de trivialidades: toda la energía nuclear depende de esta pequeña diferencia.
3 Ecuación\ ref {eq:3.2} en realidad se encuentra que se mantiene también a nivel microscópico (o cuántico), aunque allí preferimos declarar el resultado diciendo que la conservación del impulso se mantiene (ver la siguiente sección).