4.1: Energía cinética

Durante mucho tiempo en el desarrollo de la mecánica clásica, los físicos fueron conscientes de la existencia de dos cantidades distintas que se podían definir para un objeto de inercia\(m\) y velocidad\(v\). Uno era el impulso,\(mv\), y el otro era algo proporcional a\(mv^2\). A pesar de sus obvias similitudes, estas dos cantidades exhibieron diferentes propiedades y parecían estar capturando diferentes aspectos del movimiento.

Cuando las cosas finalmente se resolvieron, en la segunda mitad del siglo XIX, la cantidad\(\frac{1}{2}mv^2\) llegó a reconocerse como una forma de energía —en sí misma quizás el concepto más importante en toda la física. La energía cinética, como se le llama a esta cantidad, puede ser el tipo de energía más obvia e intuitivamente comprensible, por lo que es un buen lugar para comenzar nuestro estudio del tema.

Usaremos la letra\(K\) para denotar energía cinética, y, como es una forma de energía, la expresaremos en las unidades especialmente nombradas para este propósito, es decir julios (J). 1 julio es 1 kg·m ² /s ². En la definición

\[ K=\frac{1}{2} m v^{2} \label{eq:4.1} \]

la letra\(v\) está destinada a representar la magnitud del vector de velocidad, es decir, la velocidad de la partícula. De ahí que, a diferencia del momento, la energía cinética no es un vector, sino un escalar: no hay sentido de dirección asociado a ella. En tres dimensiones, se podría escribir

\[ K=\frac{1}{2} m\left(v_{x}^{2}+v_{y}^{2}+v_{z}^{2}\right) \label{eq:4.2} \]

Hay, por lo tanto, cierta cantidad de energía cinética asociada a cada componente del vector de velocidad, pero al final se suman todas juntas en una suma global.

Para un sistema de partículas, trataremos la energía cinética como una cantidad aditiva, tal como lo hicimos para el impulso, por lo que la energía cinética total de un sistema solo será la suma de las energías cinéticas de todas las partículas que componen el sistema. Obsérvese que, a diferencia del momentum, esta es una suma escalar (no un vector), y lo más importante, que la energía cinética es, por definición, siempre positiva, por lo que no se puede cuestionar una “cancelación” de la energía cinética de una partícula por otra, nuevamente a diferencia de lo que sucedió con el momentum. Dos objetos de igual masa que se mueven con velocidades iguales en direcciones opuestas tienen un impulso total de cero, pero su energía cinética total es definitivamente distinta de cero. Básicamente, la energía cinética de un sistema nunca puede ser cero siempre y cuando haya algún tipo de movimiento en el sistema.

Energía cinética en colisiones

Para obtener más información sobre el concepto de energía cinética, y las formas en que es diferente del impulso, es útil mirarlo en el mismo escenario en el que “descubrimos” el impulso, es decir, colisiones unidimensionales en un sistema aislado. Si volvemos a mirar la colisión representada en la Figura 3.1.1 del Capítulo 3, que se reproduce a continuación,

Figura 3.1.1)

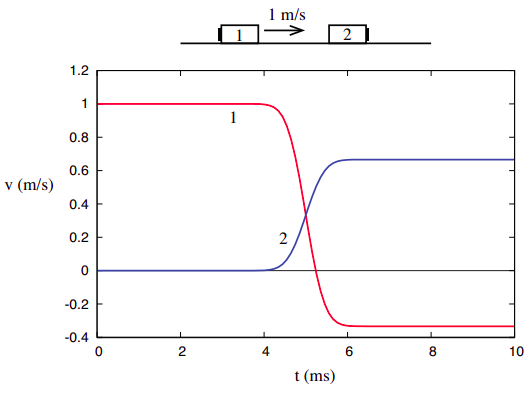
podemos usar la definición (\ ref {eq:4.1}) para calcular los valores iniciales y finales de\(K\) para cada objeto, y para el sistema en su conjunto. Recuerde que encontramos que, para este sistema en particular,\(m_2 = 2m_1\), por lo que podemos simplemente establecer\(m_1 \) = 1 kg y\(m_2\) = 2 kg, por simplicidad. Las velocidades inicial y final son\(v_{1i}\) = 1 m/s,\(v_{2i}\) = 0,\(v_{1f}\) = −1/3 m/s,\(v_{2f}\) = 2/3 m/s, y así las energías cinéticas son

\[ K_{1 i}=\frac{1}{2} \: \mathrm{J}, K_{2 i}=0 ; \quad K_{1 f}=\frac{1}{18} \: \mathrm{J}, K_{2 f}=\frac{4}{9} \: \mathrm{J} \nonumber .\]

Tenga en cuenta que 1/18 + 4/9 = 9/18 = 1/2, y así

\[ K_{s y s, i}=K_{1 i}+K_{2 i}=\frac{1}{2} \: \mathrm{J}=K_{1 f}+K_{2 f}=K_{s y s, f} \nonumber .\]

En palabras, encontramos que, en esta colisión, el valor final de la energía cinética total es el mismo que su valor inicial, y así parece que hemos “descubierto” otra cantidad conservada (además del impulso) para este sistema.

Esta creencia puede reforzarse si miramos a continuación la colisión representada en la Figura 3.1.2 del Capítulo 3, nuevamente reproducida a continuación. Recordemos que señalé en ese entonces que podemos pensar en esto como realmente la misma colisión que se representa en la Figura 3.1.1, solo mirado desde otro marco de referencia (uno moviéndose inicialmente a la derecha a 1 m/s). Tendremos más que decir sobre cómo transformar las cantidades de un marco de referencia a otro al final del capítulo.

Figura 3.1.2.)

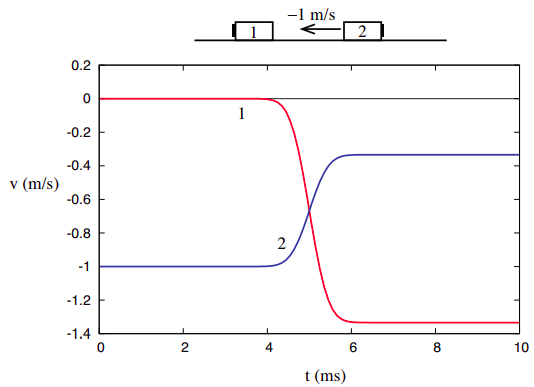
En cualquier caso, como se observó allí, todo lo que necesitamos hacer es sumar −1 m/s a todas las velocidades del problema anterior, así que tenemos\(v_{1i}\) = 0,\(v_{2i}\) = −1 m/s,\(v_{1f}\) = −4/3 m/s,\(v_{2f}\) = −1/3 m/s Las energías cinéticas correspondientes son, en consecuencia,\(K_{1i}\) = 0,\(K_{2i}\) = 1 J,\(K_{1f}\) = \(\frac{8}{9}\)J,\(K_{2f}\) =\(\frac{1}{9}\) J. Todos estos son diferentes de los valores que teníamos en el ejemplo anterior, pero tenga en cuenta que una vez más la energía cinética total después de la colisión es igual a la energía cinética total anterior, es decir, 1 J en este caso ¹.

Las cosas son, sin embargo, muy diferentes cuando consideramos el tercer ejemplo de colisión que se muestra en el Capítulo 3, es decir, aquel en el que los dos objetos se pegan juntos después de la colisión.

Figura 3.1.3)

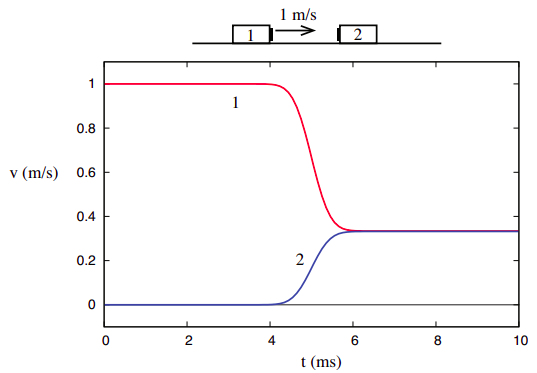
Su velocidad final conjunta, consistente con la conservación del momento, es\(v_{1f}\) =\(v_{2f}\) = 1/3 m/s, ya que el sistema inicia como en la Figura\(\PageIndex{1}\), su energía cinética es inicialmente\(K_{sys,i} = \frac{1}{2}\) J, pero después de la colisión solo tenemos

\[ K_{s y s, f}=\frac{1}{2}(3 \: \mathrm{kg})\left(\frac{1}{3} \: \frac{\mathrm{m}}{\mathrm{s}}\right)^{2}=\frac{1}{6} \: \mathrm{J} \nonumber .\]

Lo que esto muestra, sin embargo, es que a diferencia del impulso total de un sistema, que no se ve afectado por las interacciones internas, la energía cinética total sí depende de los detalles de la interacción, y así transmite cierta información sobre su naturaleza. Luego podemos refinar nuestro estudio de colisiones para distinguir dos tipos: aquellos en los que la energía cinética inicial se recupera después de la colisión, que llamaremos elástica, y aquellas donde no lo es, que llamamos inelásticas. Un caso especial de colisión inelástica es el llamado totalmente inelástico, donde los dos objetos terminan pegados entre sí, como en la Figura\(\PageIndex{3}\). Como veremos más adelante, el “déficit” de energía cinética es mayor en ese caso.

He dicho anteriormente que en una colisión elástica se “recupera” la energía cinética, y prefiero esta terminología a “conservada”, porque, de hecho, a diferencia del impulso total, la energía cinética total de un sistema no permanece constante durante toda la interacción, ni siquiera durante una colisión elástica. El ejemplo más sencillo para mostrar esto sería una colisión elástica, frontal, entre dos objetos de igual masa, moviéndose a la misma velocidad uno hacia el otro. En el transcurso de la colisión, ambos objetos se detienen momentáneamente antes de que inviertan dirección y reboten, y en ese instante, la energía cinética total es cero.

También puede examinar Figuras\(\PageIndex{1}\) y\(\PageIndex{2}\) superiores, y calcular, a partir de las gráficas, el valor de la energía cinética total durante la colisión. Verás que baja a un mínimo, y luego vuelve a su valor inicial (ver también Figura\(\PageIndex{4}\), más adelante en este capítulo). Convencionalmente, podemos hablar de la energía cinética como “conservada” en colisiones elásticas, pero es importante darnos cuenta de que estamos viendo un tipo de “conservación” diferente a la que tuvimos con el impulso total, que era constante antes, durante y después de la interacción, siempre y cuando el sistema permaneciera aislado.

Las colisiones elásticas sí sugieren que, cualquiera que sea la naturaleza última de esta cosa que llamamos “energía”, puede ser posible almacenarla de alguna forma (en este caso, durante el transcurso de la colisión), y luego recuperarla, como energía cinética, eventualmente. Esto allana el camino para la introducción de otros tipos de “energía” además de la energía cinética, como veremos en un capítulo posterior, y la posibilidad de que se produzca una interconversión entre estos tipos. Por el momento, simplemente diremos que en una colisión elástica alguna cantidad de energía cinética se almacena temporalmente como algún tipo de “energía interna”, y después de la colisión esta se convierte de nuevo en energía cinética; mientras que, en una colisión inelástica, alguna cantidad de energía cinética se convierte irrevocablemente en algo de “energía interna”, y nunca la recuperamos.

Dado que lo que ocurra en última instancia depende de los detalles y la naturaleza de la interacción, se nos llevará a distinguir entre interacciones “conservadoras”, donde la energía cinética se almacena reversiblemente como alguna otra forma de energía en alguna parte, e interacciones “disipativas”, donde la conversión de energía es, al menos en parte, irreversible. Claramente, las colisiones elásticas están asociadas con interacciones conservadoras y las colisiones inelásticas están asociadas con interacciones disipativas. Esta clasificación preliminar de interacciones deberá revisarse un poco más cuidadosamente, sin embargo, en el siguiente capítulo.

---

¹ Esto es, por supuesto, consistente con el principio de relatividad del que te hablé en el Capítulo 2: si el proceso en la Figura\(\PageIndex{2}\) es realmente el mismo que el de la Figura\(\PageIndex{1}\), solo visto en un marco de referencia inercial diferente, entonces, si se ve que la energía se conserva en uno marco, también debe verse que se conserva en el otro. Más sobre esto en la Sección 4.2.

---

Velocidad relativa y coeficiente de restitución

Una propiedad interesante de las colisiones elásticas se puede dar a conocer a partir de un cuidadoso estudio de figuras\(\PageIndex{1}\) y\(\PageIndex{2}\). En ambos casos, como puede ver, la velocidad relativa de los dos objetos que colisionan tiene la misma magnitud (pero signo opuesto) antes y después de la colisión. Es decir: en una colisión elástica, los objetos terminan separándose al mismo ritmo que originalmente se juntaron.

Recordemos que, en el Capítulo 1, definimos la velocidad del objeto 2 en relación con el objeto 1 como la cantidad

\[ v_{12}=v_{2}-v_{1} \label{eq:4.3} \]

(compare la Ecuación (1.3.8); y de manera similar la velocidad del objeto 1 en relación con el objeto 2 es\(v_{21} = v_1 − v_2\). Con esta definición se puede comprobar que, efectivamente, las colisiones mostradas en las Figs. \(\PageIndex{1}\)y\(\PageIndex{2}\) satisfacer la igualdad

\[ v_{12, i}=-v_{12, f} \label{eq:4.4} \]

(tenga en cuenta que igualmente bien podríamos haber usado\(v_{21}\) en lugar de\(v_{12}\)). Por ejemplo, en la Figura\(\PageIndex{1}\),\(v_{12,i} = v_{2i} − v_{1i}\) = −1 m/s, mientras que\(v_{12,f}\) = 2/3 − (−1/3) = 1 m/s Así que los objetos inicialmente se mueven uno hacia el otro a una velocidad de 1 m por segundo, y terminan separándose igual de rápido, a 1 m por segundo. Visualmente, debes notar que la distancia entre las curvas roja y azul es la misma antes y después (pero no durante) de la colisión; el hecho de que crucen explica la diferencia en signo de la velocidad relativa, lo que a su vez significa simplemente que antes de la colisión se estaban uniendo, y después se están separando.

Solo se necesita un poco de álgebra para mostrar que la Ecuación (\ ref {eq:4.4}) se deriva de las condiciones conjuntas de conservación del impulso y conservación de la energía cinética. El primero (\(p_i\)=\(p_f\)) claramente tiene la forma

\[ m_{1} v_{1 i}+m_{2} v_{2 i}=m_{1} v_{1 f}+m_{2} v_{2 f} \label{eq:4.5} \]

mientras que el segundo (\(K_i\)=\(K_f\)) puede escribirse como

\[ \frac{1}{2} m_{1} v_{1 i}^{2}+\frac{1}{2} m_{2} v_{2 i}^{2}=\frac{1}{2} m_{1} v_{1 f}^{2}+\frac{1}{2} m_{2} v_{2 f}^{2} \label{eq:4.6} .\]

Podemos cancelar todos los factores de 1/2 en la Ecuación (\ ref {eq:4.6}) ², luego reorganizarlo para que las cantidades pertenecientes al objeto 1 estén en un lado, y las cantidades pertenecientes al objeto 2 estén en el otro. Obtenemos

\ begin {array} {c}
{m_ {1}\ izquierda (v_ {1 i} ^ {2} -v_ {1 f} ^ {2}\ derecha) =-m_ {2}\ izquierda (v_ {2 i} ^ {2} -v_ {2 f} ^ {2}\ derecha)}\\
{m_ {1}\ izquierda (v_ {1 i} -v_ _ {1 f}\ derecha)\ izquierda (v_ {1 i} +v_ {1 f}\ derecha) =-m_ {2}\ izquierda (v_ {2 i} -v_ {2 f}\ derecha)\ izquierda (v_ {2 i} +v_ {2 f}\ derecha)}\ label {eq:4.7}
\ end {array}

(utilizando el hecho de que\(a^2 − b^2 = (a + b)(a − b) \)). Tenga en cuenta, sin embargo, que la ecuación (\ ref {eq:4.5}) también se puede reescribir como

\[ m_{1}\left(v_{1 i}-v_{1 f}\right)=-m_{2}\left(v_{2 i}-v_{2 f}\right) \nonumber .\]

Esto inmediatamente nos permite cancelar los factores correspondientes en Eq (\ ref {eq:4.7}), así que nos quedamos con\(v_{1i} + v_{1f} = v_{2i} + v_{2f} \), los cuales pueden ser reescritos como

\[ v_{1 f}-v_{2 f}=v_{2 i}-v_{1 i} \label{eq:4.8} \]

y esto es equivalente a (\ ref {eq:4.4})

Entonces, en una colisión elástica la velocidad a la que los dos objetos se separan es la misma que la velocidad a la que se juntaron, mientras que, en lo que claramente es el extremo opuesto, en una colisión totalmente inelástica la velocidad relativa final es cero —los objetos no se separan en absoluto después de que chocan. Esto sugiere que podemos cuantificar cuán inelástica es una colisión por la relación de la magnitud final a la inicial de la velocidad relativa. Esta relación se denota por\(e\) y se llama el coeficiente de restitución. Formalmente,

\[ e=-\frac{v_{12, f}}{v_{12, i}}=-\frac{v_{2 f}-v_{1 f}}{v_{2 i}-v_{1 i}} \label{eq:4.9} .\]

Para una colisión elástica,\(e\) = 1, como lo requiere la Ecuación (\ ref {eq:4.4}). Para una colisión totalmente inelástica, como la representada en la Figura\(\PageIndex{3}\),\(e\) = 0. Para una colisión que sea inelástica, pero no totalmente inelástica,\(e\) tendrá algún valor entre estos dos extremos. Este conocimiento puede ser utilizado para “diseñar” colisiones inelásticas (¡por ejemplo, para problemas con la tarea!) : simplemente elija un valor para\(e\), entre 0 y 1, en la Ecuación (\ ref {eq:4.9}), y combine esta ecuación con la conservación del requerimiento de impulso (\ ref {eq:4.5}). Las dos ecuaciones le permiten calcular las velocidades finales para cualquier valor de\(m_1\),\(m_2\), y las velocidades iniciales. La\(\PageIndex{4}\) siguiente figura, por ejemplo, muestra cómo\(\PageIndex{1}\) habría sido la colisión en la figura, si el coeficiente de restitución hubiera sido 0.6 en lugar de 1. Se puede verificar, resolviendo (\ ref {eq:4.5}) y (\ ref {eq:4.9}) juntos, y usando las velocidades iniciales, que\(v_{1f}\) = −1/15 m/s = −0.0667 m/s, y\(v_{2f}\) = 8/15 m/s = 0.533 m/s.

Figura\(\PageIndex{1}\).

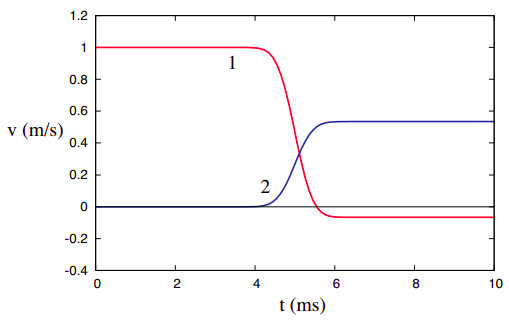
Si bien, como acabo de mencionar, para la mayoría de colisiones “normales” el coeficiente de restitución será un número positivo entre 1 y 0, puede haber excepciones a esto. Si uno de los objetos pasa por el otro (como una bala a través de un objetivo, por ejemplo), el valor de\(e\) será negativo (aunque todavía entre 0 y 1 en magnitud). Y\(e\) puede ser mayor que 1 para las llamadas “colisiones explosivas”, donde se libera cierta cantidad de energía extra, y se convierte en energía cinética, a medida que chocan los objetos. (Por ejemplo, dos jugadores de hockey chocan en la pista y se alejan entre sí). En este caso, los objetos bien pueden separarse volando más rápido de lo que se juntaron.

Un ejemplo extremo de una situación con\(e\) > 0 es una separación explosiva, que es cuando los dos objetos inicialmente se mueven juntos y luego se separan volando. En ese caso, el denominador de la Ecuación (\ ref {eq:4.9}) es cero, y así\(e\) es formalmente infinito. Esto sugiere, lo que en realidad es el caso, es decir, que aunque los procesos explosivos son ciertamente importantes, describirlos a través del coeficiente de restitución es raro, incluso cuando sería formalmente posible. En la práctica, el uso del coeficiente de restitución se limita principalmente al rango elástico a completamente inelástico, es decir, 0 ≤\(e\) ≤ 1.

---

² Quizás te estés preguntando, ¿por qué definimos la energía cinética con un factor 1/2 al frente, de todos modos? No hay una buena respuesta en este punto. Digamos que más adelante hará más sencilla la definición de “energía potencial”, particularmente en lo que respecta a su relación con la fuerza.