4.2: Energía Cinética “Convertible” y “Traslacional”
- Page ID
- 128279
La figura\(\PageIndex{1}\) muestra cómo varía la energía cinética total con el tiempo, para los dos objetos mostrados colisionando en la figura 4.1.1, dependiendo de los detalles de la colisión, es decir, del valor de\(e\). Las tres curvas mostradas cubren la caja elástica,\(e\) = 1 (Figura 4.1.1), la caja totalmente inelástica,\(e\) = 0 (Figura 4.3), y la caja inelástica con\(e\) = 0.6 de la Figura 4.1.4. Recordemos que el impulso total se conserva en los tres casos.
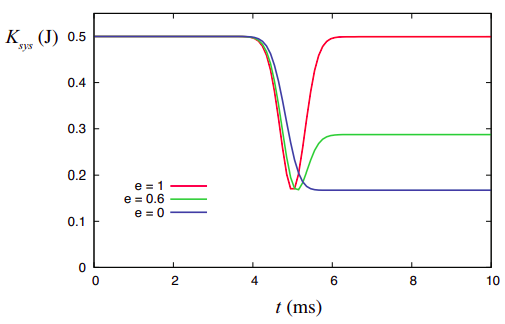
La figura\(\PageIndex{1}\) muestra que la mayor pérdida de energía cinética ocurre por la colisión totalmente inelástica, que, como veremos en un momento, es, de hecho, un resultado general. Siendo ese el caso, la cifra también muestra que puede que no siempre sea posible bajar a cero la energía cinética total, incluso temporalmente. La razón de esto es que, si se conserva el impulso, la velocidad del centro de masa no puede cambiar, por lo que si el centro de masa se estaba moviendo antes de la colisión, debe seguir moviéndose después; y, como se menciona en la introducción de este capítulo, siempre y cuando haya movimiento en un sistema, su energía cinética total no puede ser cero.
Todo esto sugiere que debería ser posible dividir la energía cinética total de un sistema en dos partes: una parte asociada al movimiento del centro de masa, que no puede cambiar en ninguna colisión conservadora de momento, y una parte asociada con el movimiento relativo de las partes que conforman el sistema. Esta segunda parte se desvanecería irreversiblemente en una colisión totalmente inelástica, mientras que recuperaría su valor original en una colisión elástica.
La manera de ver esto matemáticamente, para un sistema de dos objetos con masas\(m_1\) y\(m_2\), es introducir el centro de la velocidad de masa\(v_{cm}\) [Ecuación (3.3.3)]
\[ v_{c m}=\frac{m_{1} v_{1}+m_{2} v_{2}}{m_{1}+m_{2}} \nonumber \]
y la velocidad relativa\(v_{12} = v_2 − v_1\) (Ecuación (4.1.3) anterior), y observar que las velocidades\(v_1\) y\(v_2\) pueden escribirse, respectivamente, como
Sustituyendo las ecuaciones (\ ref {eq:4.10}) en la expresión\(K_{sys} = \frac{1}{2}m_1 v_1^2 + \frac{1}{2}m_2v_2^2\), uno encuentra que los términos cruzados desaparecen, y todo lo que queda es
\[ K_{s y s}=\frac{1}{2}\left(m_{1}+m_{2}\right) v_{c m}^{2}+\frac{1}{2} \frac{m_{1} m_{2}^{2}+m_{2} m_{1}^{2}}{\left(m_{1}+m_{2}\right)^{2}} v_{12}^{2} \nonumber .\]
Un factor de (\(m_1 + m_2\)) puede ser cancelado en el último término, y la expresión final toma la forma
\[ K_{s y s}=K_{c m}+K_{c o n v} \label{eq:4.11} \]
donde la energía cinética del centro de masa (o energía de traslación) es justo lo que uno tendría si todo el sistema fuera una sola partícula de masa\(M = m_1 + m_2\) moviéndose al centro de la velocidad de la masa:
\[ K_{c m}=\frac{1}{2} M v_{c m}^{2} \label{eq:4.12} \]
y la “energía convertible”\(K_{conv}\) es la parte asociada al movimiento relativo, que puede hacerse que desaparezca por completo en una colisión inelástica 3:
\[ K_{\text {conv}}=\frac{1}{2} \frac{m_{1} m_{2}}{m_{1}+m_{2}} v_{12}^{2}=\frac{1}{2} \mu v_{12}^{2} \label{eq:4.13} .\]
La última ecuación define implícitamente una cantidad útil que llamamos la masa reducida de un sistema de dos partículas, y denotan por\(µ\):
\[ \mu=\frac{m_{1} m_{2}}{m_{1}+m_{2}} \label{eq:4.14} .\]
Ecuación (\ ref {eq:4.11}), con las definiciones (\ ref {eq:4.12}) y (\ ref {eq:4.13}), explica prácticamente todo lo que vemos pasando en la Figura\(\PageIndex{1}\). La energía cinética total es la suma de dos términos, el primero de los cuales\(K_{cm}\),, nunca puede cambiar: es, de hecho, tan constante como el impulso total mismo, ya que involucra el centro de la velocidad másica\(v_{cm}\), que es proporcional al impulso total del sistema (ecuación de recuerdo (3.3.4 )). El término que puede, y sí cambia, es el segundo, la energía convertible. De hecho, en una colisión ordinaria en la que los objetos no pasan entre sí, debe haber al menos un instante en el tiempo cuando\(K_{conv}\) = 0. Esto se debe a que involucra la velocidad relativa, y dado que la velocidad relativa debe cambiar de signo en algún momento (los objetos inicialmente se están uniendo, pero terminan separándose), debe ser cero en ese momento.
Esto explica por qué todas las curvas de la Figura\(\PageIndex{1}\) tienen el mismo valor mínimo (aunque puedan alcanzarlo en diferentes momentos): ese valor es claramente\(K_{cm}\) para el sistema (ya que\(K_{conv}\) es cero en ese momento). Es lo mismo para todas las curvas porque todos los sistemas considerados tienen la misma masa total e impulso (según lo determinado por las velocidades iniciales), simplemente los elegimos de esa manera.
Dado que\(K_{cm}\) no puede cambiar para un sistema aislado, la energía cinética máxima que se puede perder en una colisión en dicho sistema es el valor inicial de\(K_{conv}\), que denotaríamos como\(K_{conv,i}\). Esto es, de hecho, completamente perdido en una colisión totalmente inelástica, ya que en ese caso\(v_{12,f}\) = 0, y la Ecuación (\ ref {eq:4.13}) da entonces\(K_{conv,f}\) = 0. De hecho, usando la Ecuación (4.1.9), podemos relacionar el valor final de la energía convertible con su valor inicial a través del coeficiente de restitución:
\[ K_{\text {conv}, f}=\frac{1}{2} \mu v_{12, f}^{2}=\frac{1}{2} \mu e^{2} v_{12, i}^{2}=e^{2} K_{\text {conv}, i} \label{eq:4.15} .\]
Así, por ejemplo, en una colisión con\(e\) = 0.6, el valor final de la energía convertible sería sólo 0.36 veces su valor inicial: 64% de ella se habría “perdido”. (Esto no es, sin embargo, lo mismo que el 64% de la energía inicial total, ya que esta última aún incluye\(K_{cm}\), que no cambia). También podemos escribir la Ecuación (\ ref {eq:4.15}) como
\[ \Delta K_{s y s}=\left(e^{2}-1\right) K_{c o n v, i}=\left(e^{2}-1\right) \frac{1}{2} \mu v_{12, i}^{2} \label{eq:4.16} \]
ya que el único cambio posible en\(K_{sys}\) debe provenir de la energía convertible.
Aunque hemos derivado la descomposición (\ ref {eq:4.11}) para la situación muy restringida de dos objetos moviéndose en una dimensión, el resultado básico es bastante general: primero, todo en la derivación funciona si\(v_1\) y\(v_2\) son reemplazados por vectores\(\vec v_1\) y\(\vec v_2\), así los resultados se mantienen en tres dimensiones también. Segundo, para un sistema de cualquier número de partículas, todavía se puede escribir\(K_{sys}\) como\(K_{cm}+\) otro término que depende únicamente del movimiento relativo de todos los pares de partículas. Esta “energía convertible generalizada”, o energía cinética del movimiento relativo tendría la forma
\[ K_{r e l}=\frac{1}{2} \mu_{12} v_{12}^{2}+\frac{1}{2} \mu_{13} v_{13}^{2}+\ldots+\frac{1}{2} \mu_{23} v_{23}^{2}+\ldots \nonumber \]
(en esta expresión, algo así como\(\mu_{23}\) significa una masa reducida como la de la Ecuación (\ ref {eq:4.14}), sólo para masas\(m_2\) y\(m_3\), etcétera).
Cuando lleguemos al estudio del movimiento rotacional, por ejemplo, veremos que la energía cinética total de un objeto rígido extendido puede escribirse como\(K_{cm} + K_{rot}\), donde\(K_{rot}\), la energía cinética rotacional, es exactamente el mismo tipo de cosas que lo que aquí hemos llamado la “energía convertible”.
Todo lo anterior aún deja sin respuesta la pregunta de qué sucede con la energía convertible que se pierde en una colisión inelástica. ¿Justo en qué es lo que se convierte? La respuesta a esta pregunta será objeto del siguiente capítulo.
3 Aunque el nombre de “energía convertible” tiene sentido en este contexto, no lo es, por lo que puedo decir, en el uso general. Lo he tomado prestado de Los principios y práctica de la física de Mazur, pero probablemente no deberías esperar encontrarlo en otros libros de texto.
Energía cinética e impulso en diferentes marcos de referencia
He señalado en repetidas ocasiones antes que todo el movimiento es relativo, y así, en cierta medida, la energía cinética y el impulso también deben ser algo relativos. Un automóvil en un tren de carga tiene mucho impulso en relación con un observador en tierra, pero su impulso relativo a otro automóvil en el mismo tren es cero, ya que no se mueven uno con relación al otro. Lo mismo podría decirse de su energía cinética.
En general, si se tiene un sistema con un impulso\(\vec p_{sys}\) e inercia totales\(M\), su centro de masa tendrá una velocidad\(\vec v_{cm} = \vec p_{sys}/M\). Entonces, si tuvieras que moverte al lado del sistema con una velocidad exactamente igual a\(\vec v_{cm}\), el impulso total del sistema relativo a ti sería cero. Si el sistema fuera un objeto sólido, no te “golpearía” si hacías contacto; no habría colisión. Aquí puede ayudar pensar, por ejemplo, en el reabastecimiento de combustible de aviones en vuelo: si las velocidades de los dos aviones coinciden exactamente, pueden hacer contacto sin ningún daño, como si estuvieran en reposo. Un marco de referencia que se mueve a la velocidad del centro de masa de un sistema se denomina, por esta razón, un marco de impulso cero para el sistema en cuestión.
Claramente, en tal marco de referencia, la energía cinética traslacional del sistema\(K_{cm} = \frac{1}{2}Mv^2_{cm}\),, también será cero (ya que, en ese marco, el centro de masa no se mueve en absoluto). Sin embargo, el término de movimiento relativo\(K_{conv}\), no se vería completamente afectado por el cambio en el marco de referencia. Esto se debe a que, como ya habrás notado, para convertir velocidades de un marco de referencia a otro simplemente sumamos o restamos de todas las velocidades la velocidad relativa de los dos fotogramas. Esta operación, sin embargo, no cambiará ninguna de las velocidades relativas de las partes del sistema, ya que estas son todas diferencias para empezar. Matemáticamente
\[ \left(v_{2}+v^{\prime}\right)-\left(v_{1}+v^{\prime}\right)=v_{2}-v_{1} \nonumber \]
independientemente del valor de\(v^{\prime}\).
Entonces hay algo que podríamos llamar absoluto (a diferencia de “relativo”) sobre la energía cinética convertible: es lo mismo, tendrá el mismo valor, para cualquier observador, independientemente de cuán rápido o en qué dirección ese observador pueda estar moviéndose en relación con el sistema en su conjunto. Podemos pensarlo como una propiedad intrínseca (significado, independiente del observador) del sistema.


